Частные производные и дифференциалы высших порядков п. Частные производные высших порядков

Вид материала

Документы

Содержание К. Правило нахождения наибольшего и наименьшего значений на компакте К

Подобный материал:

• Высшая математика II иттф (тф 9…13), эл-16, 2004-2005 уч год, 50.97kb.
• Если использовать разности высших порядков вплоть до n-го, то разностное уравнение, 1187.79kb.
• Программа-минимум кандидатского экзамена по специальности 01. 01. 01- математический, 134.95kb.
• Метод сеток для приближенного решения задачи Дирихле, 45.84kb.
• 8. обыкновенные дифференциальные уравнения, 136.95kb.
• Ном порядке и осуществляющие предпринимательскую деятельность без образования юридического, 308.53kb.
• Тематический план лекций по дисциплине „Медицинская химия для студентов 4 курса фармацевтического, 83.16kb.
• Определители 2-го и 3-го порядков: определения и применение к решению систем линейных, 42kb.
• Фельдман А. Б. Производные финансовые и товарные инструменты, 9496.35kb.
• Программа коллоквиумов по курсу физической химии, 99.84kb.

§ 11. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ

ВЫСШИХ ПОРЯДКОВ

п. 1. Частные производные высших порядков

Пусть функция z=f(x,y) – дифференцируемая в области 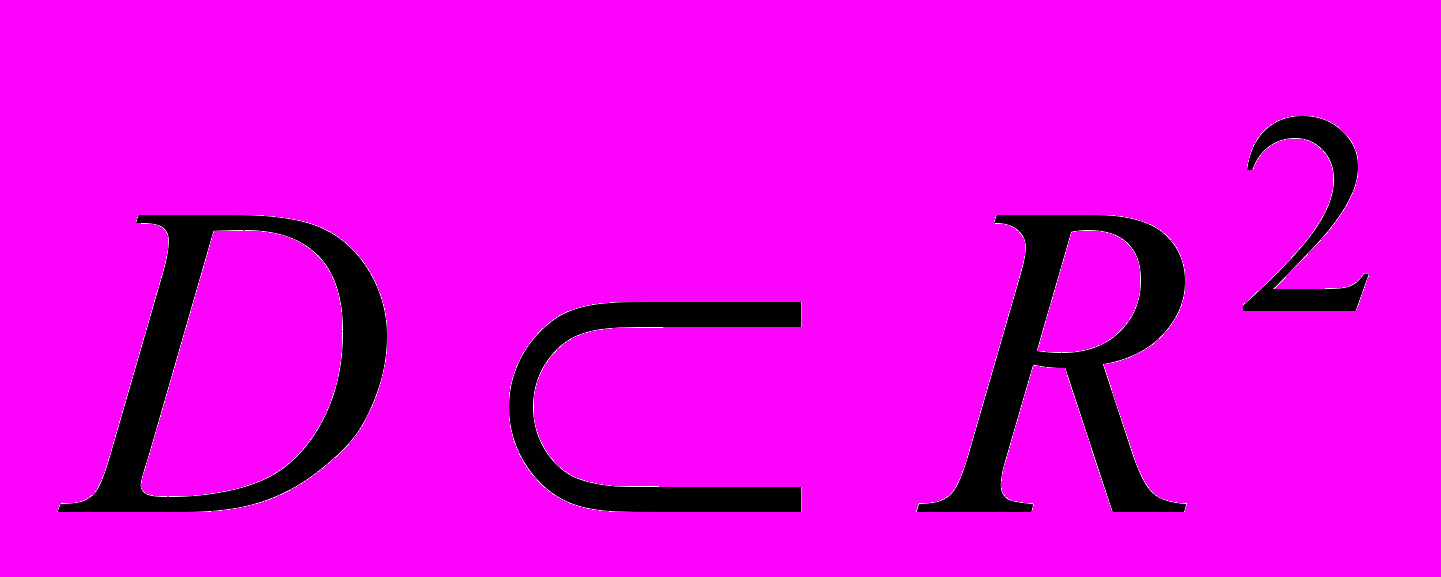. Тогда по Т. 1 § 5 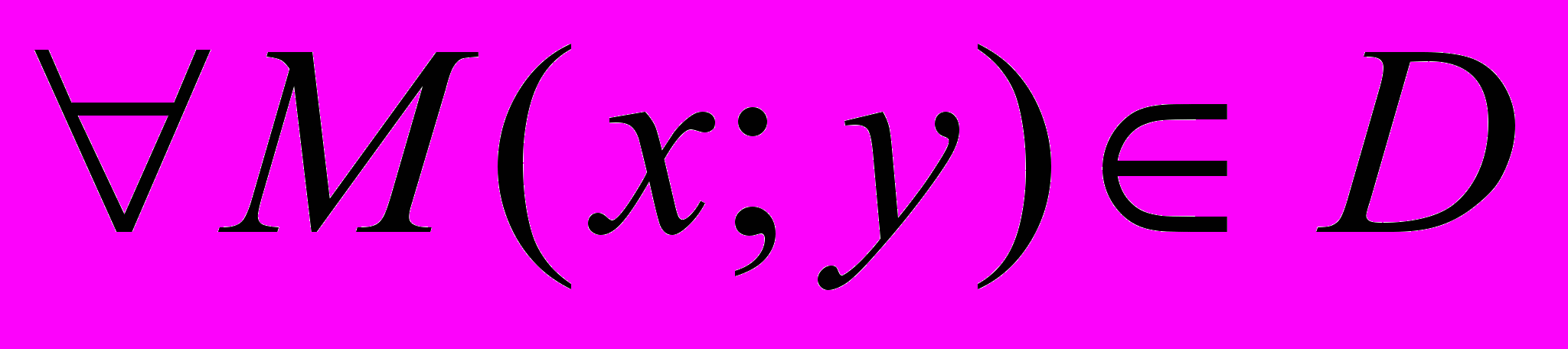 частные производные 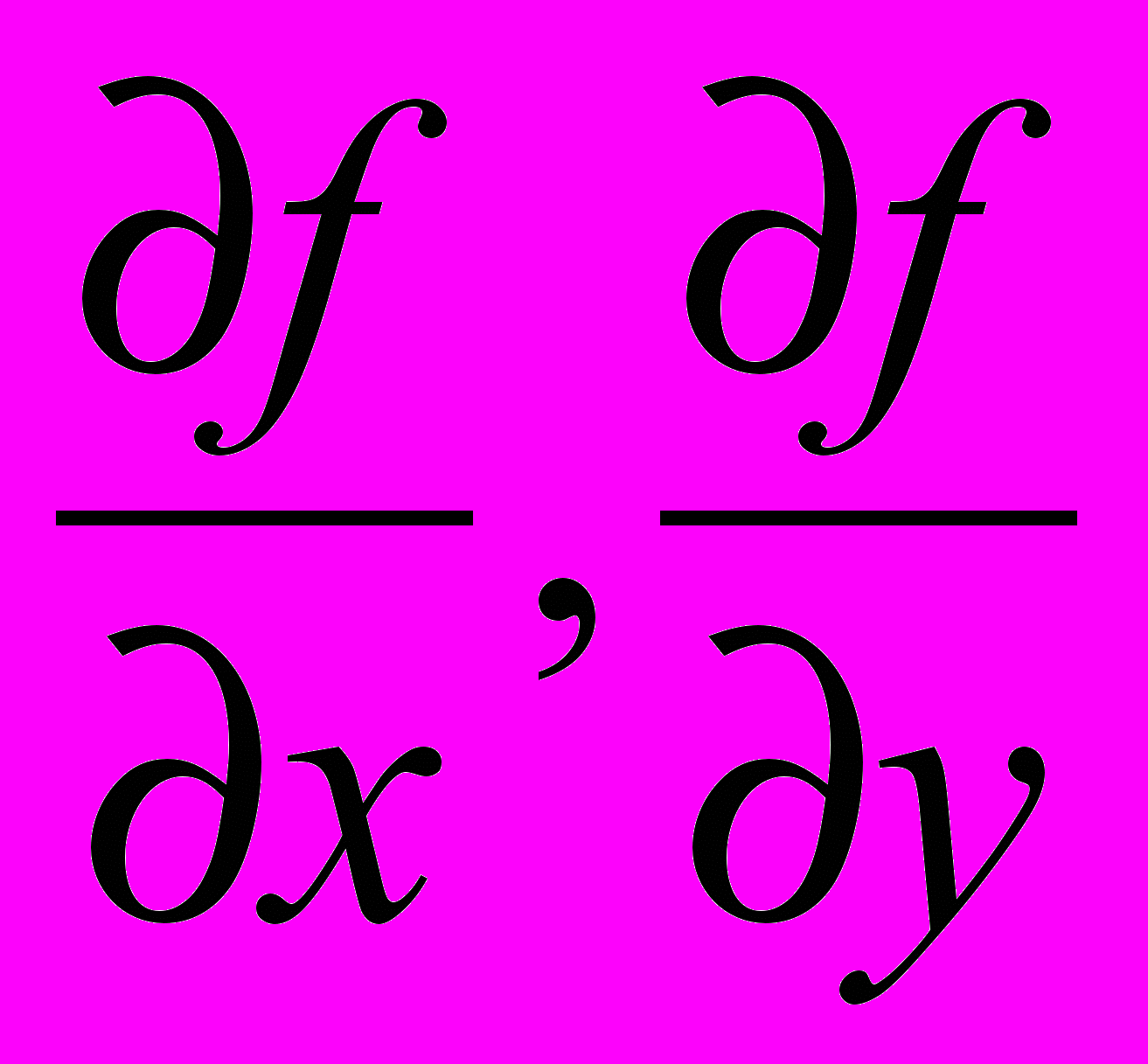– это также функции 2-х действительных переменных х и у. Если окажется, что функции 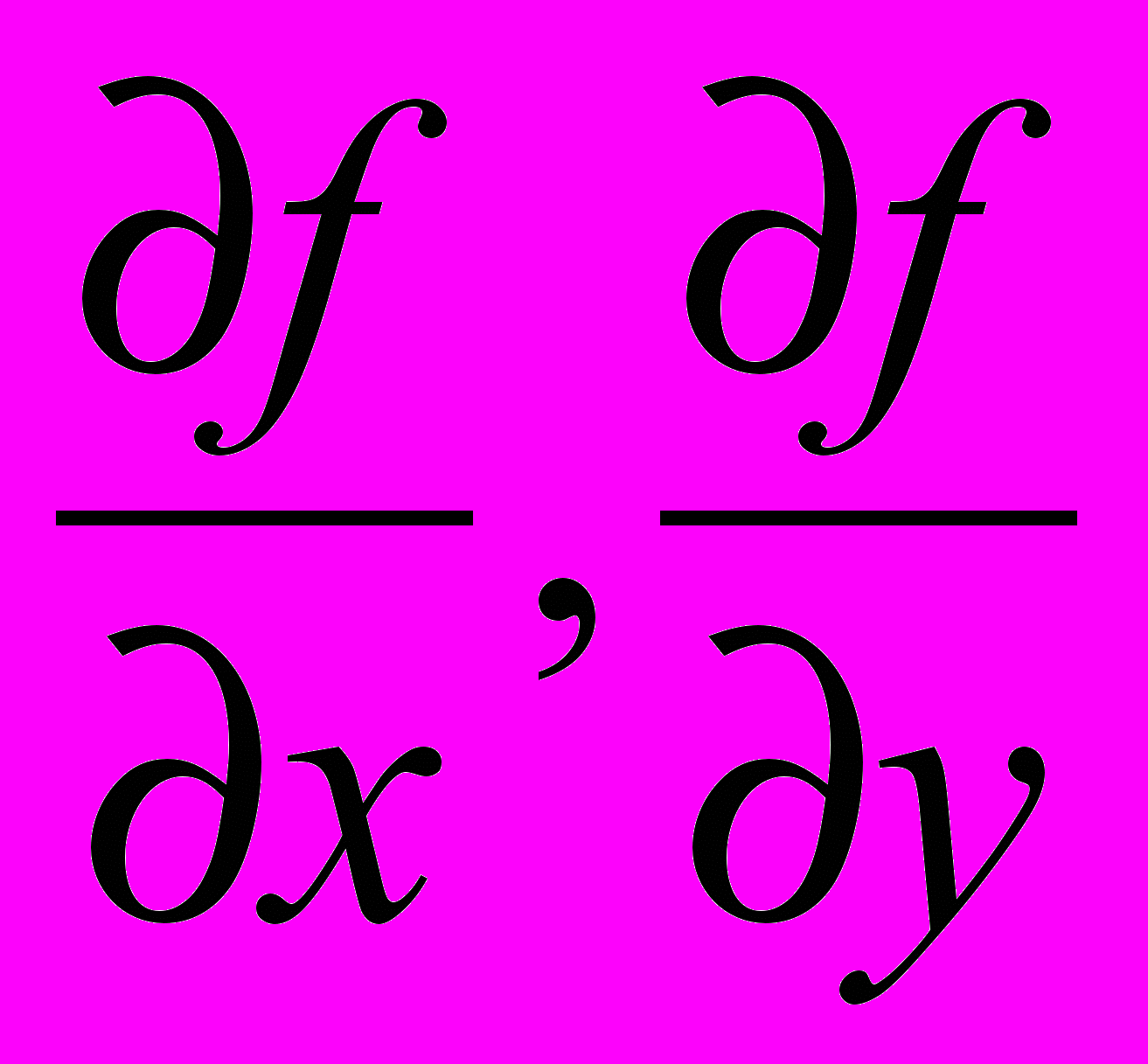– дифференцируемые в области 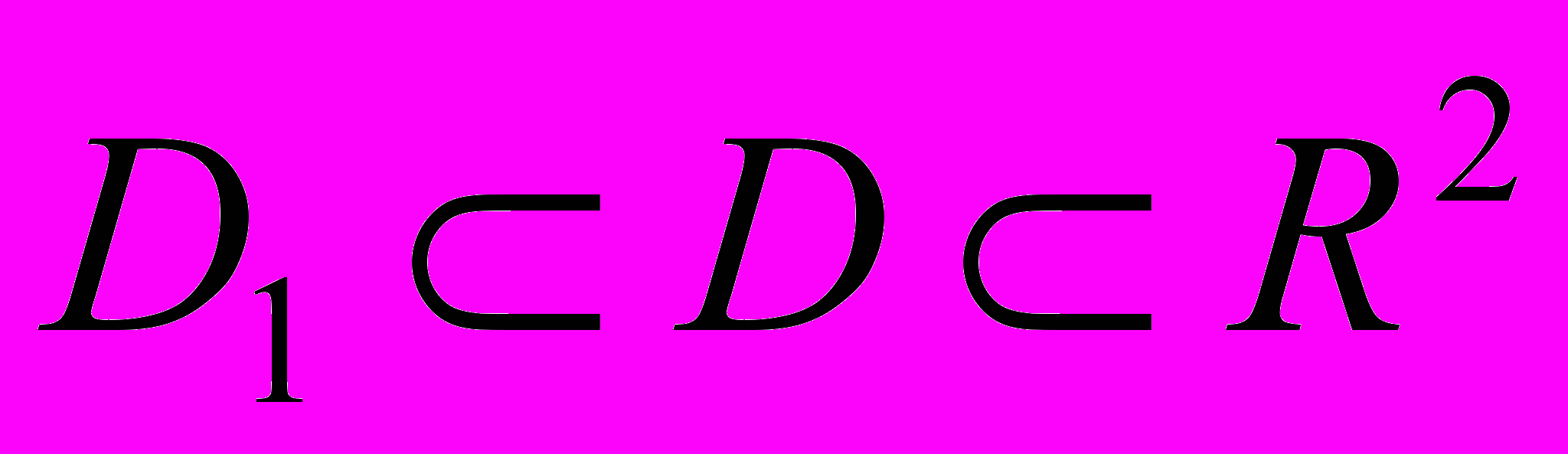, то по Т.1 § в 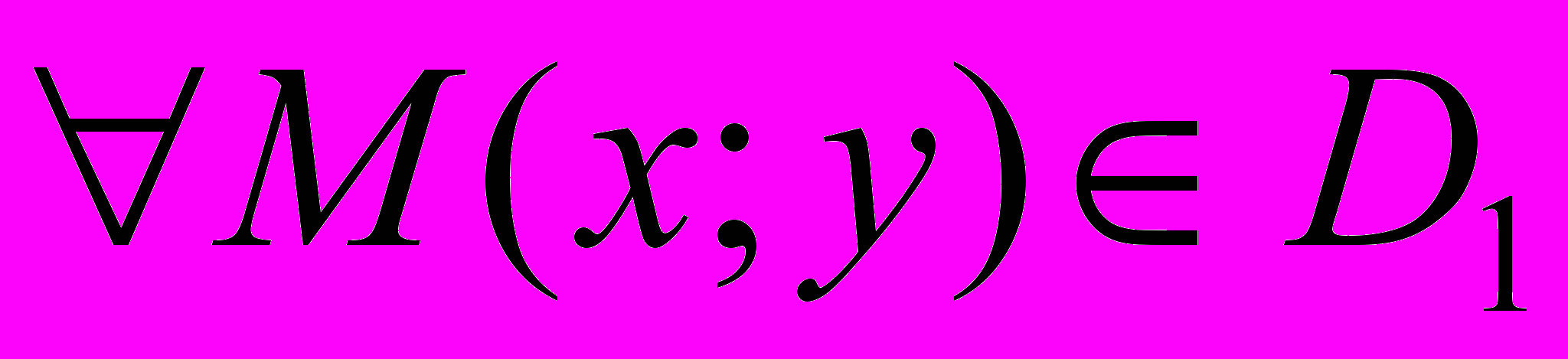 частные производные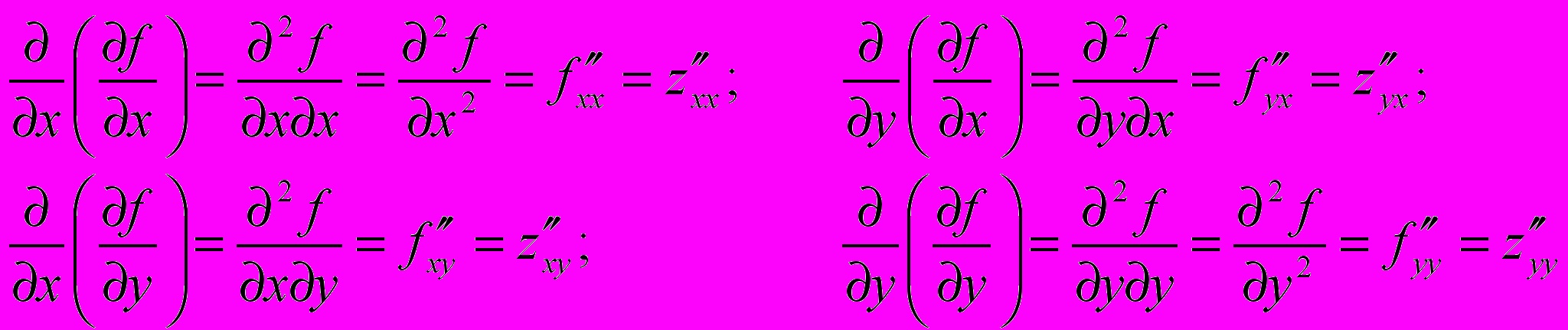



– это также функции 2-х действительных переменных х и у, их называют частными производными 2-го порядка. Частные производные и отличаются порядком дифференцирования и называются смешанными частными производными 2-го порядка. Аналогично вводятся частными производными 3-го, …, п-го порядков. Частные производные 2-го и более высокого порядков называются частными производными высшегго порядка.

Пример. Найти частные производные 3-го порядка функции z = 2 x³ y² .

Решение.


Теорема 1. Если функция z=f(x,y) имеет в некоторой окрестности точки 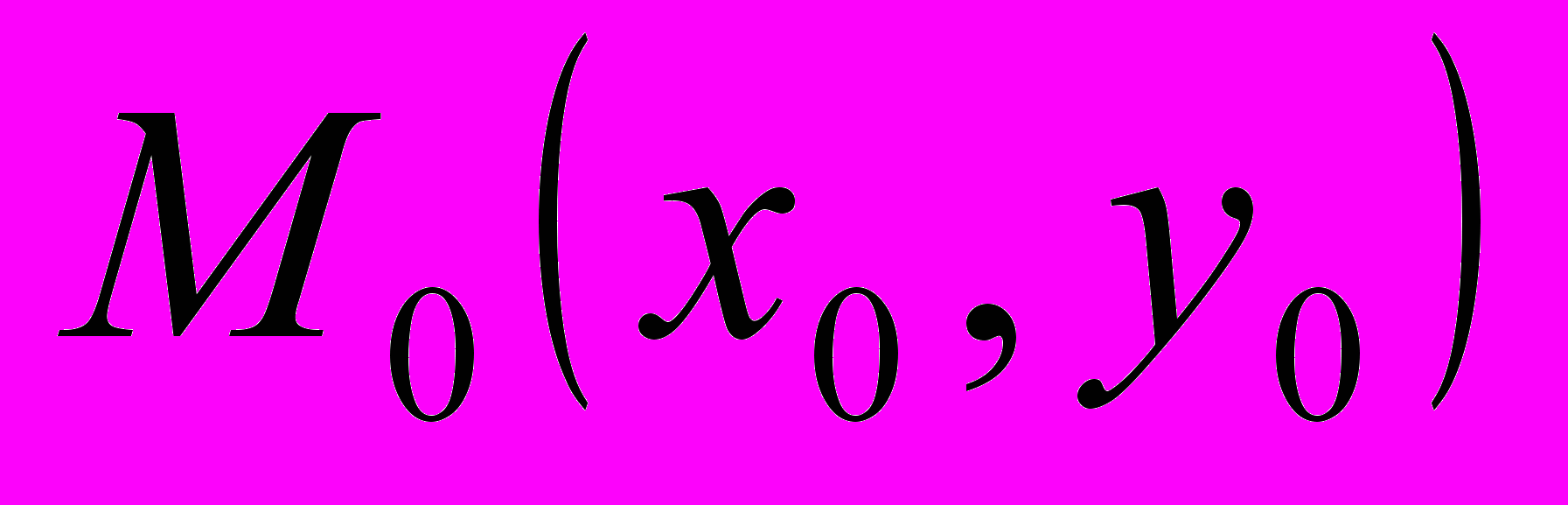смешанные частные производные 2-го порядка, причем эти частные производные – непрерывные в точке 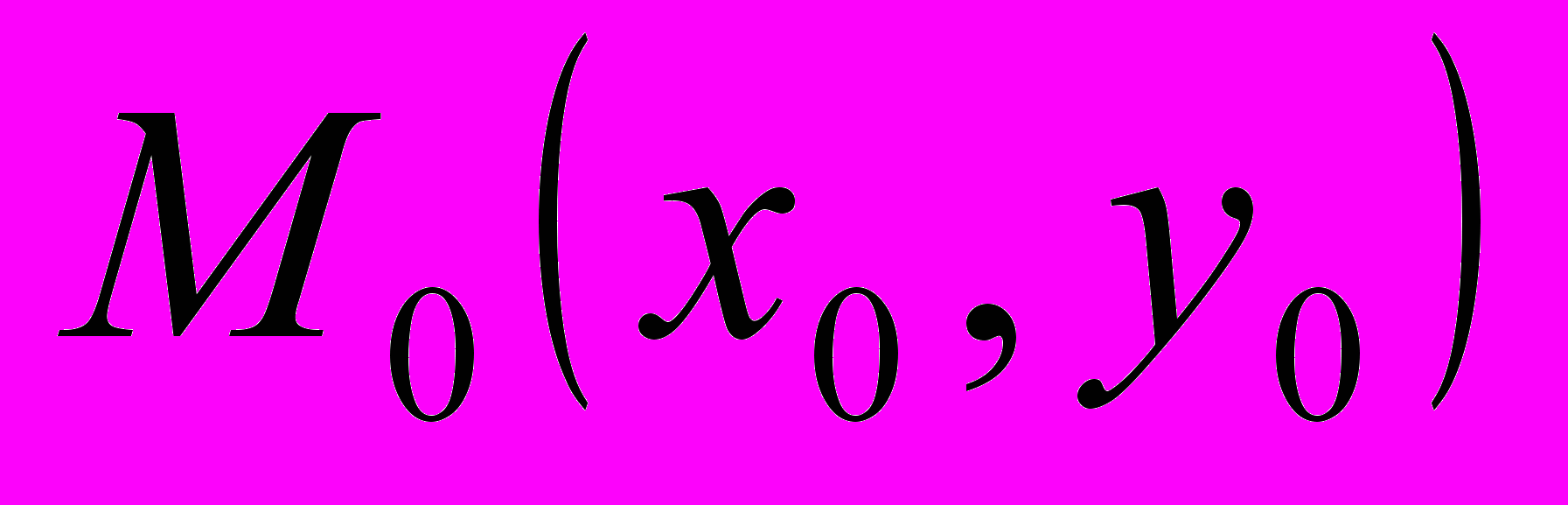, тогда в точке 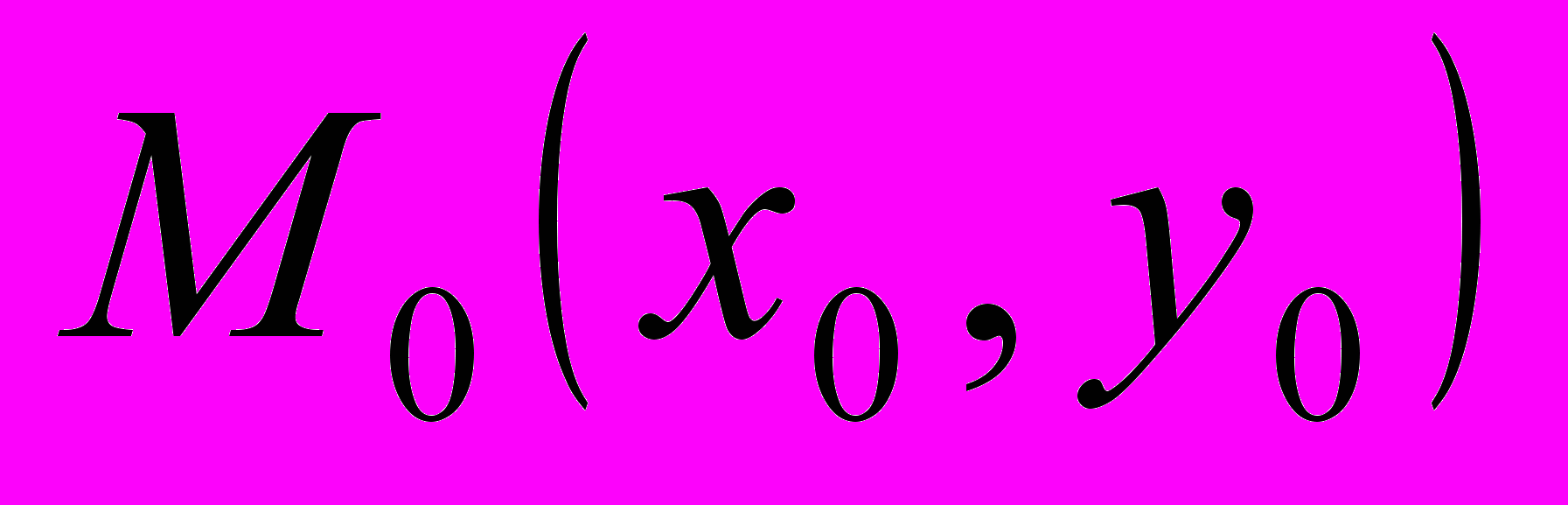смешанные частные производные равны, т.е. .

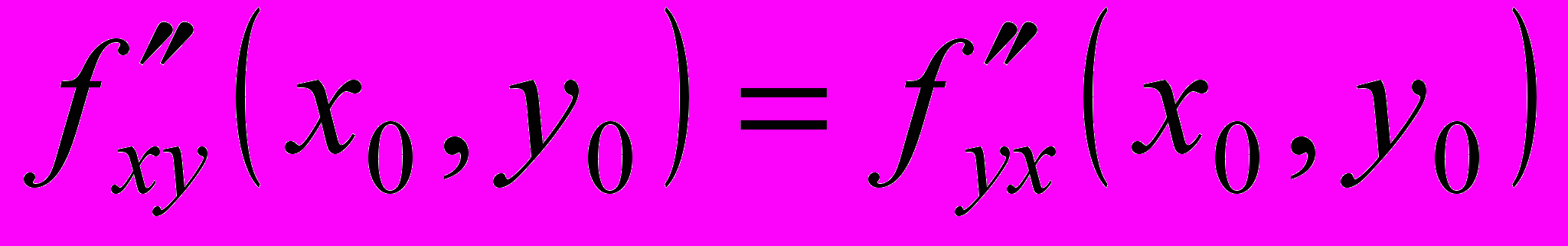Доказательство.


п. 2. Дифференциалы высших порядков

Пусть функция z=f(x,y) – дифференцируемая в области 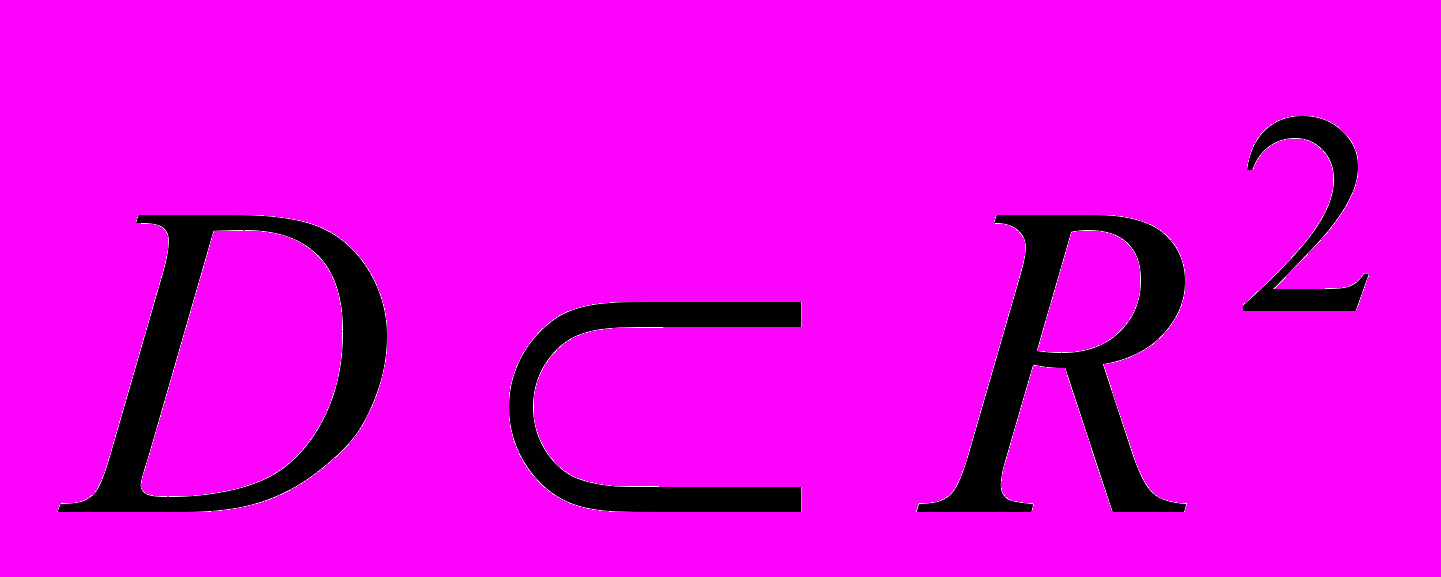. Тогда в 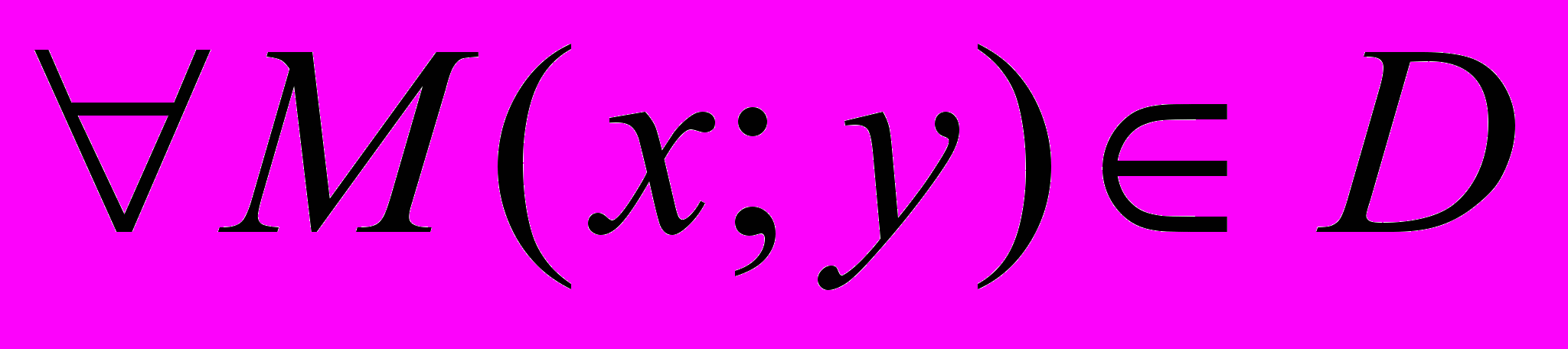ее дифференциал 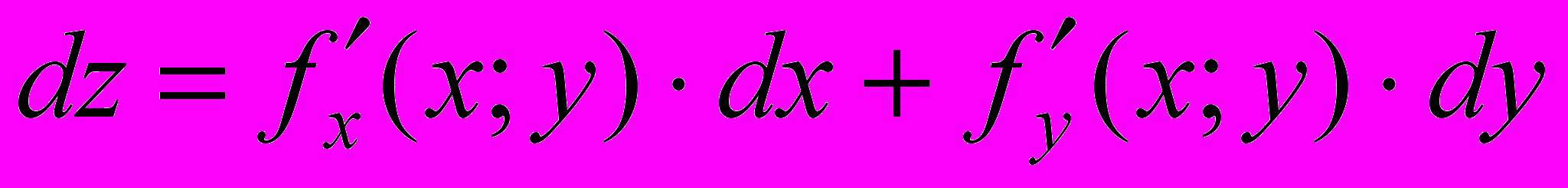, где 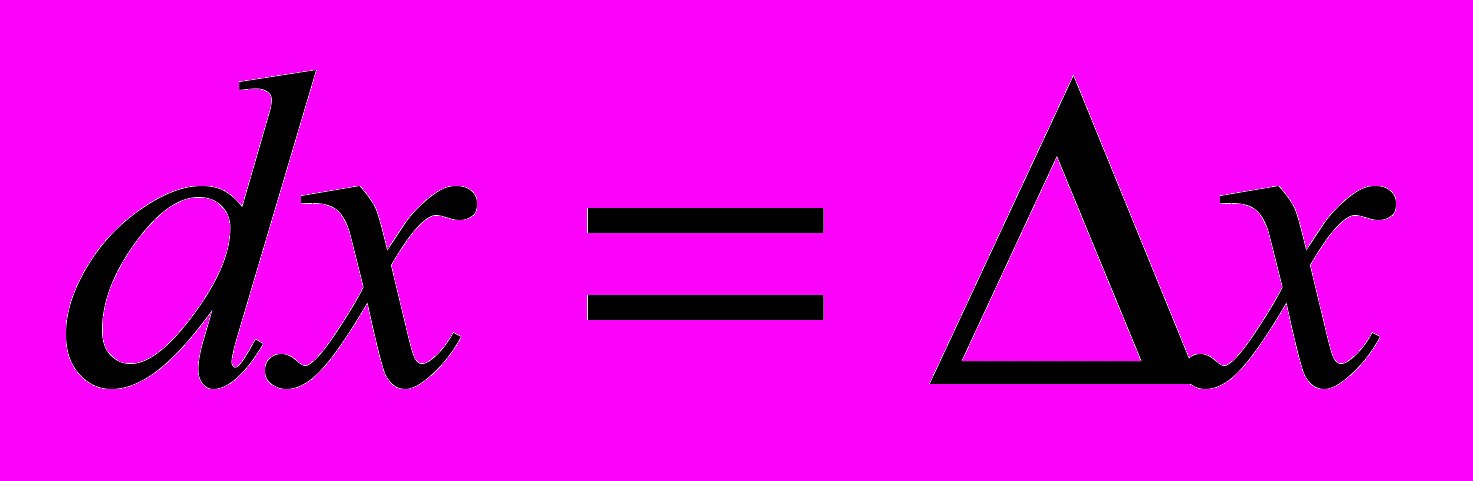, 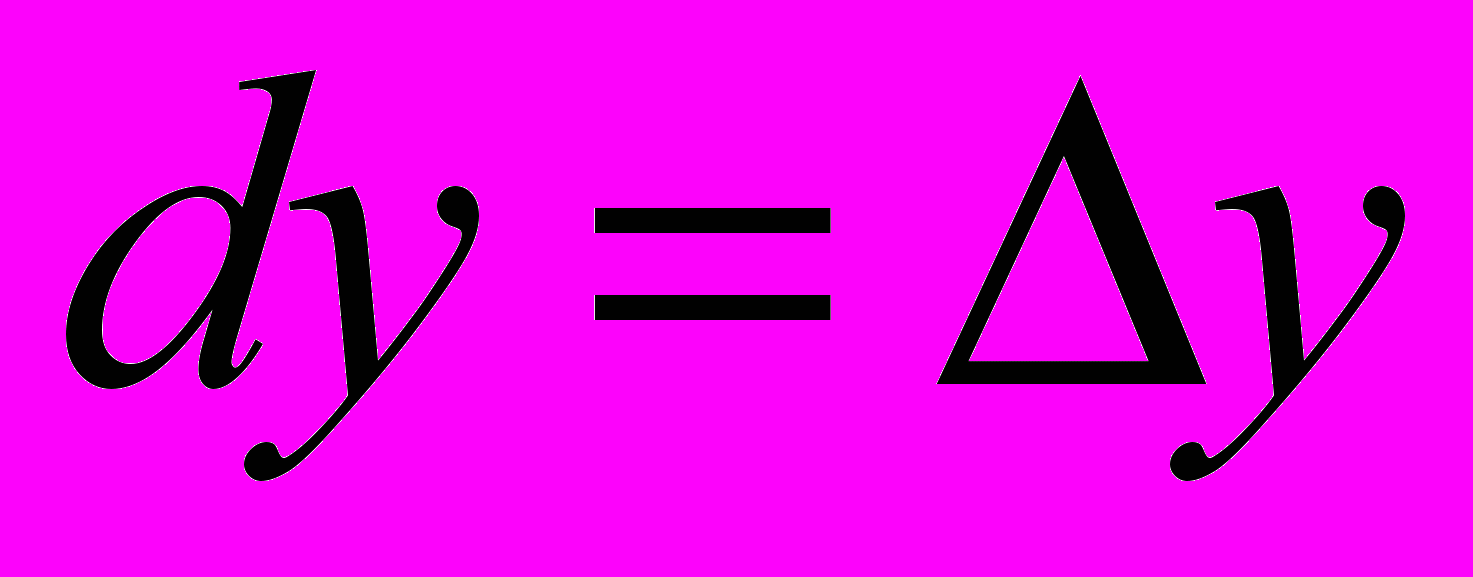– приращения аргумента х и у соответственно. Далее будем считать, что 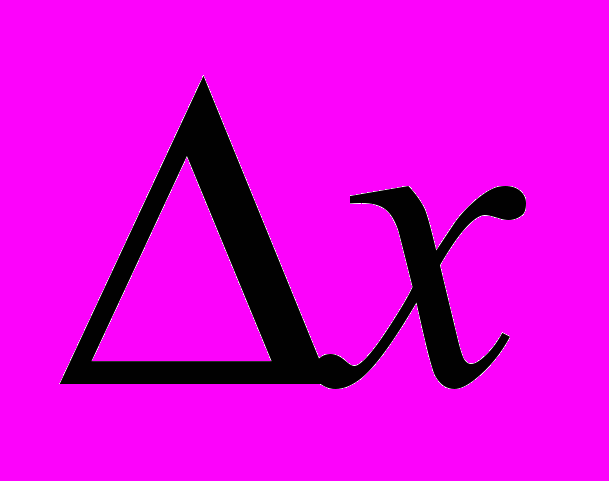, 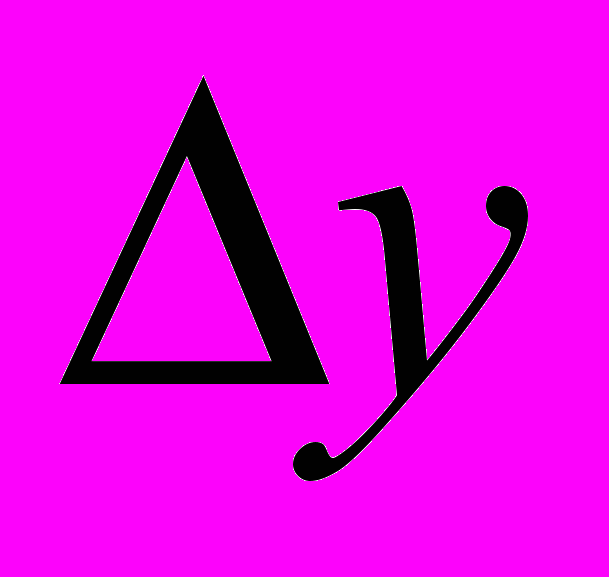–const . Тогда дифференциал dz – это также функции 2-х действительных переменных х и у. Если окажется, что функция dz – дифференцируемая в области 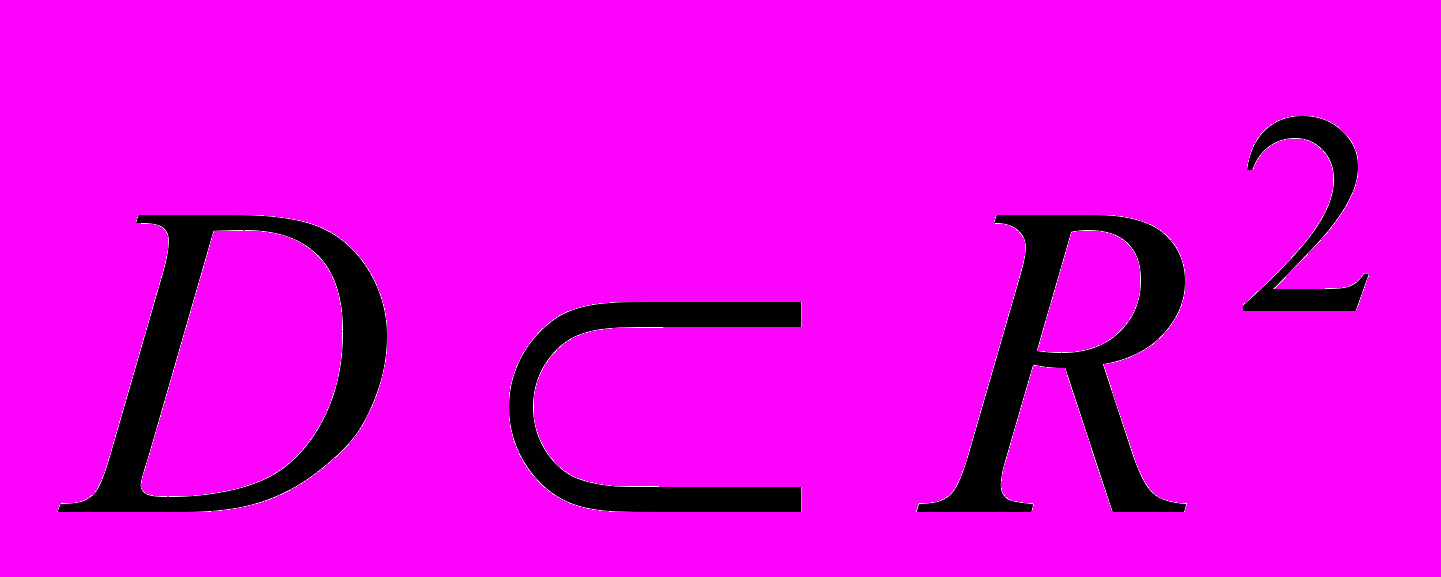, то диффернциал от диффернциала 1-го порядка называется диффернциалом 2-ого порядка и обозначается 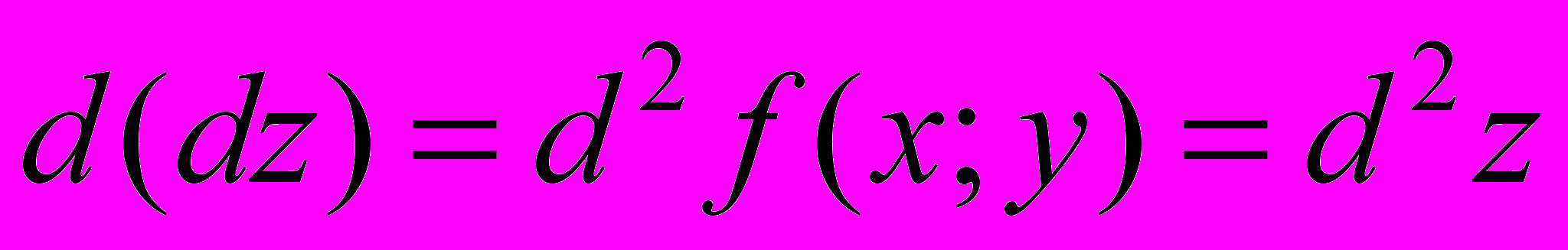. Аналогично вводится понятие дифференциала 3-го, …, п-го порядков. Дифференциалы 2-го и более высоких порядко называют дифференциалами высших порядков.

С помощью метода мат. индукции можно доказать формулу для вычисления дифференциалов высших порядков



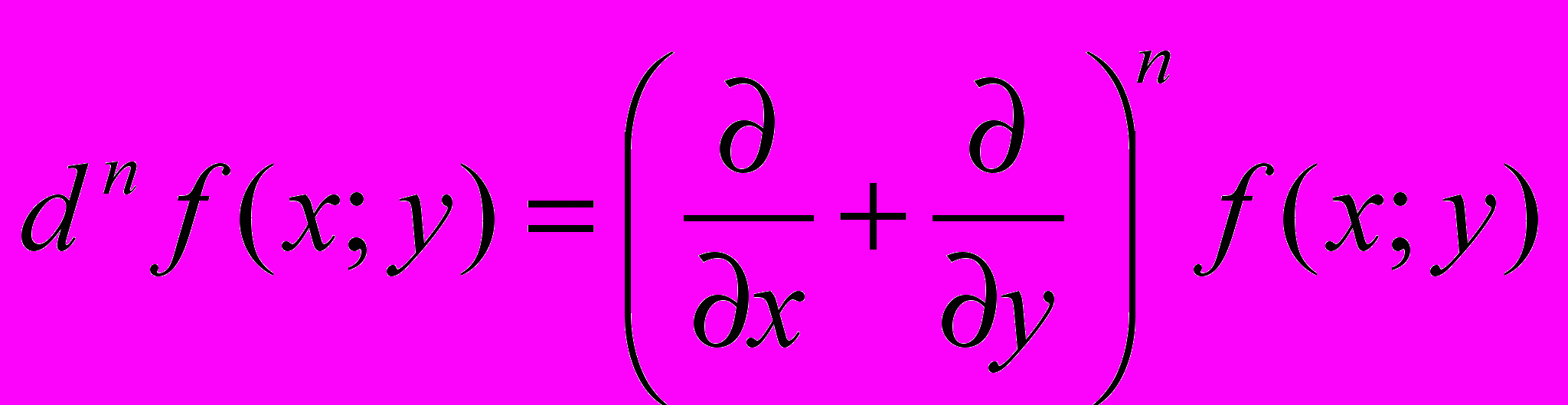
Проверим для п=2:


Как и для функции 1-ой переменной дифференциалы высших порядков не обладают свойством инвариантности формы записи. Покажем это на примере дифференциала 2-го порядка.


Замечание. Если функци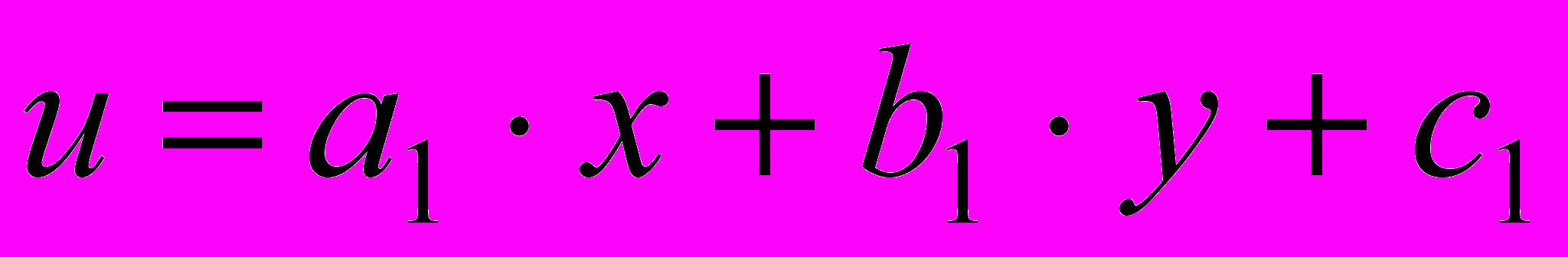и и 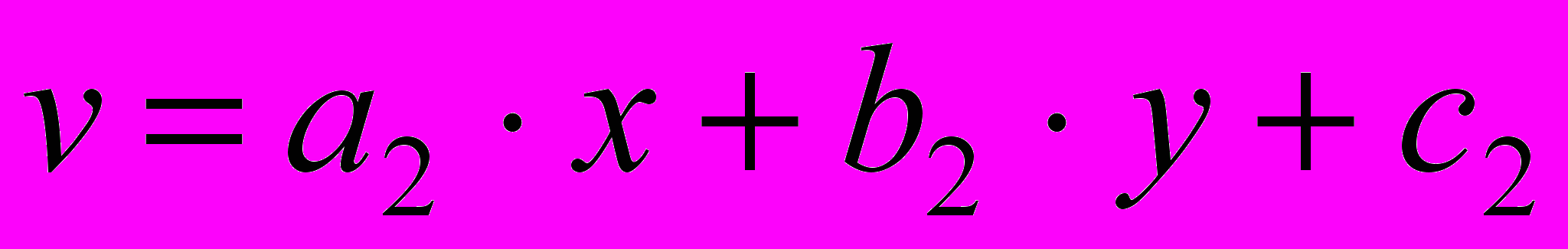являются линейными, то для дифференциалов высших порядков свойство инвариантности формы записи сохраняется, т.к. .


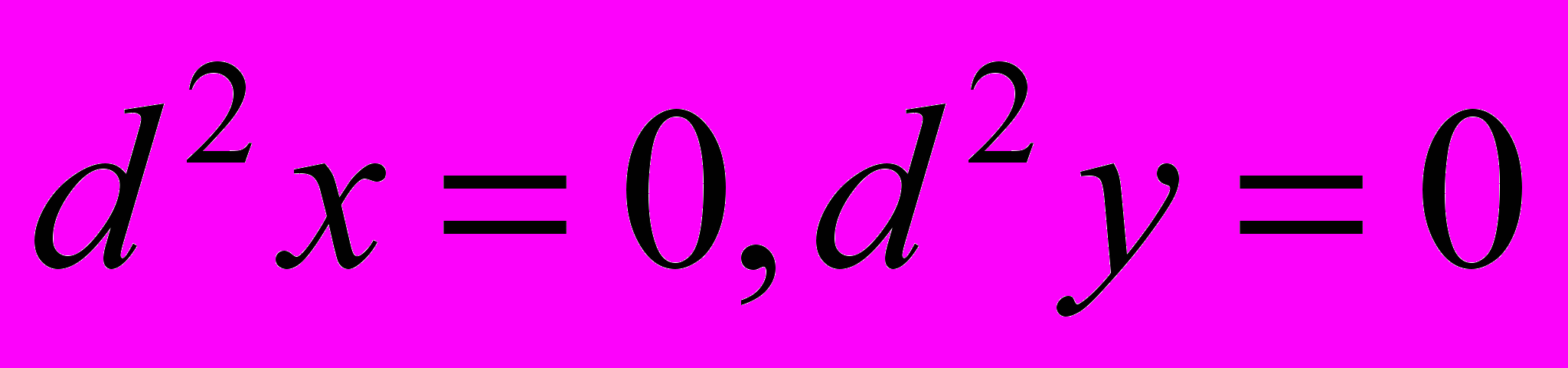§ 12. ФОРМУЛА ТЕЙЛОРА. КРИТЕРИЙ ПОСТОЯНСТВА ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

п.1. Формула Тейлора для ДФМП

Формула Тейлора для функции одной переменной имела вид

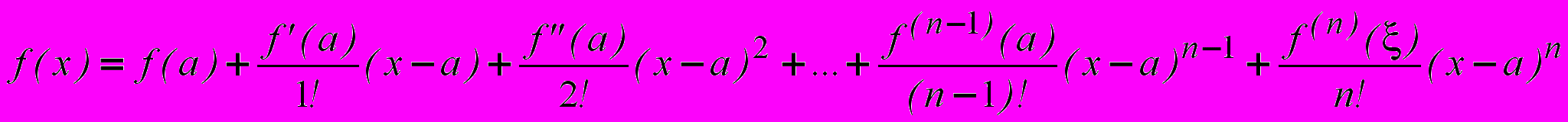, если перенести f(a) влево и считать x – a = ∆x, то тогда формулу Тейлора можно записать следующим образом

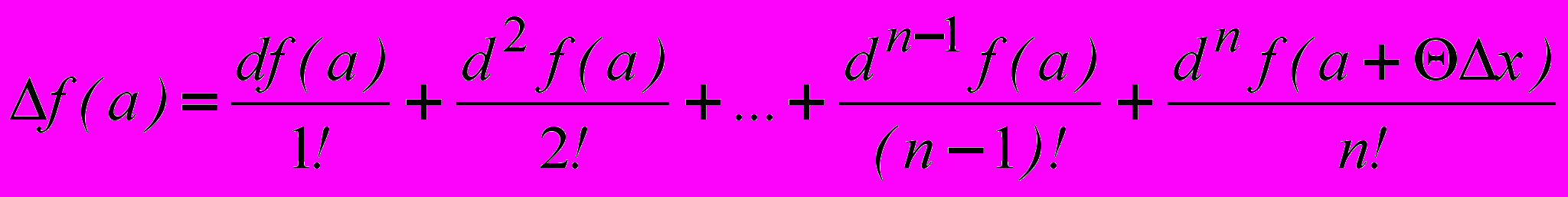, (1)

где f(x)-f(a)=∆f(a), f^(k)(a)·(x-a)^k= f^(k)(a)·∆x^k·=d^kf(a).

Для функции z=f(x,y) имеет место аналогичная формула

Теорема 1. Пусть функция z=f(x,y) n-раз непрерывно дифференцируемая в некоторой окрестности U(M₀;r) точки M₀(x₀,y₀), тогда справедлива формула

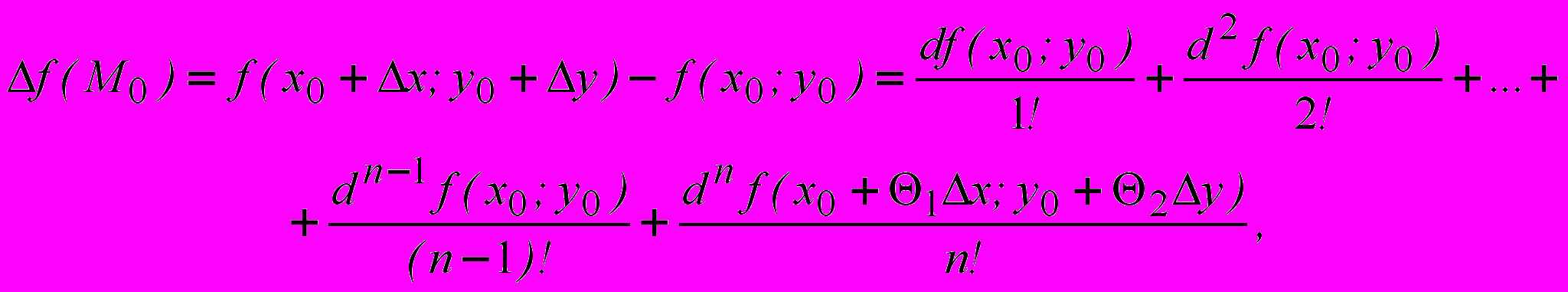(2)

где 0<Θ_i<1

Доказательство.

В данной δ -окрестности точки M₀(x₀,y₀) возьмем точку M(x₀+∆x, y₀+∆y). Пусть 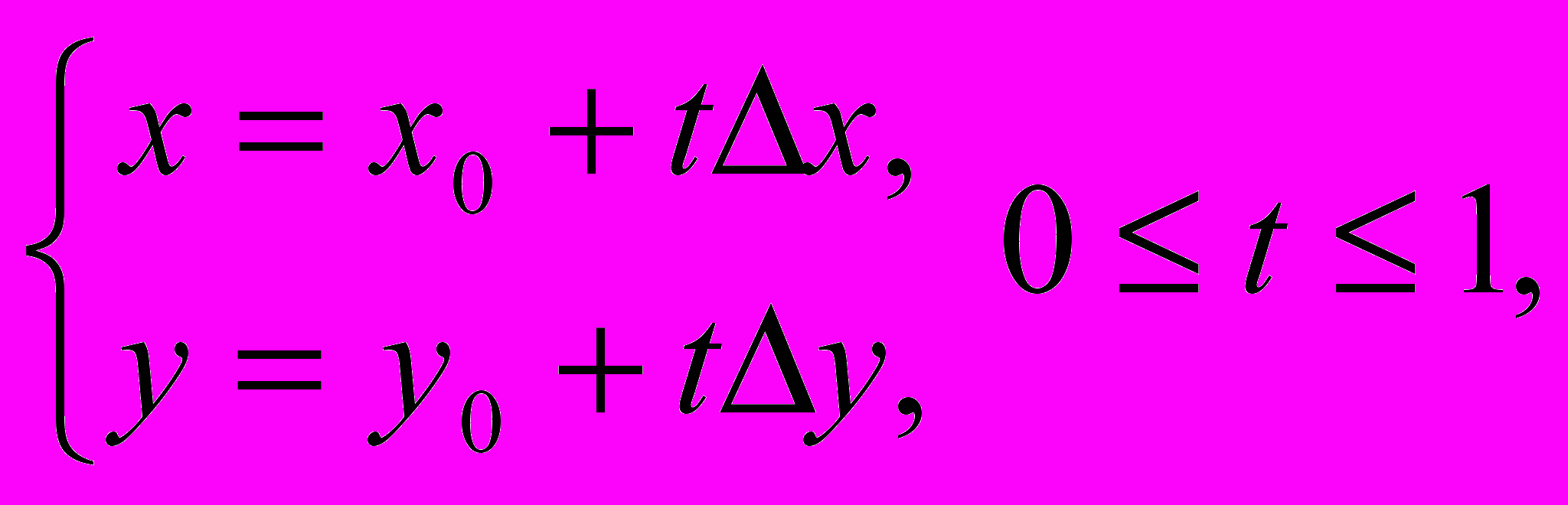тогда точка N(x,y)U(M₀;δ) и при t=0 получаем точку M₀ , а при t=1 получаем точку M. Падставим в z=f(x,y) выражения для x и y . В результате получим сложную функцию от одной переменной t:

.

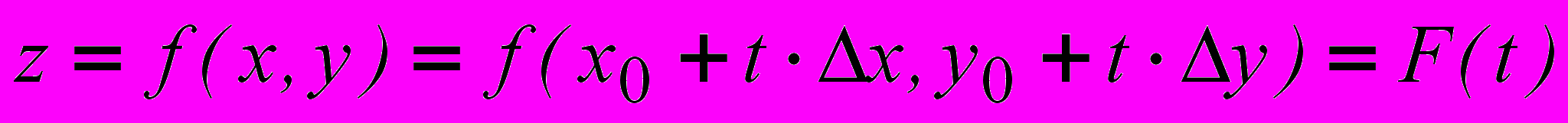Тогда прирощение функции ∆f(M₀)=F(1)-F(0)= ∆F(0) при ∆t=1 можно записать по формуле (1) следующим образом:



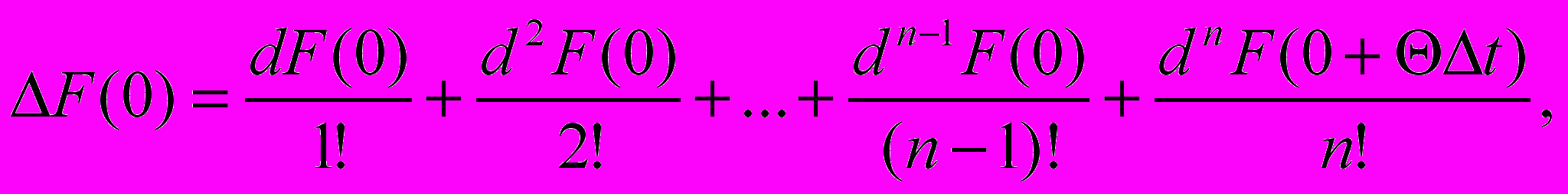
где 0<Θ<1. Вернемся в последнем равенстве к переменным x и y, так как x и y линейно зависят от t ,то инвариантность формы записи для ифференциалов высших порядков сохраняется (см замечание §11), значит имеет место формула (2).

п.2. Критерий постоянства функции 2-х переменных

Теорема 2. (критерий постоянства функции 2-х переменных) Для того, чтобы функция z=f(x,y) была постоянной в области D необходимо и достаточно, чтобы в этой области были равны 0 частные производные, или,что тоже, чтобы df(M)=0 .

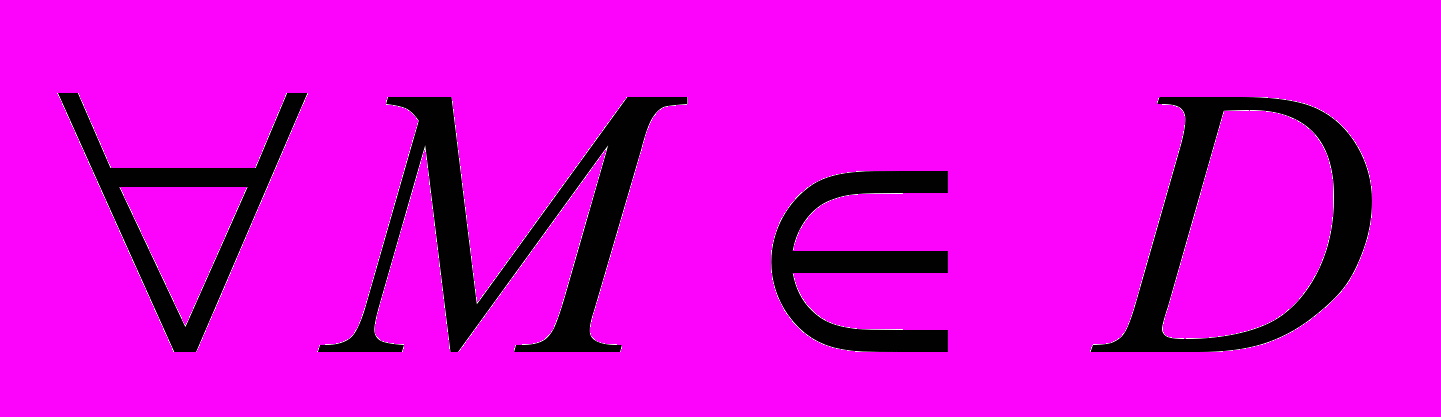Доказательство. Сначала докажем эквивалентность условий (А) и (В), где

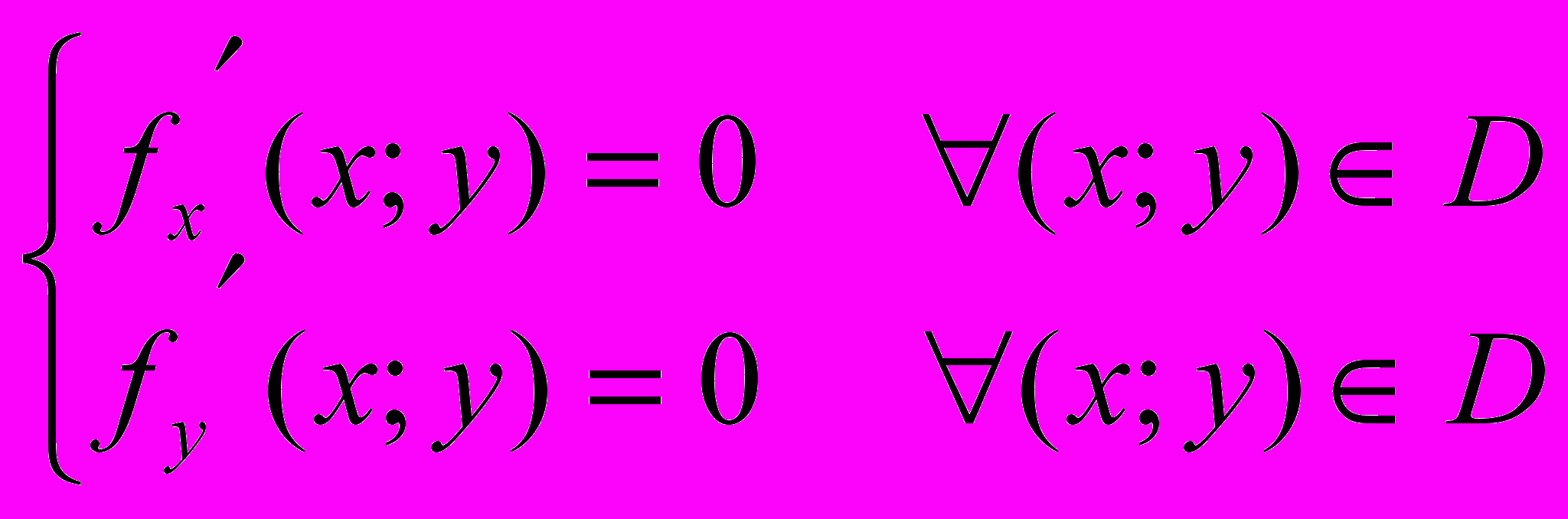
(А) (В) .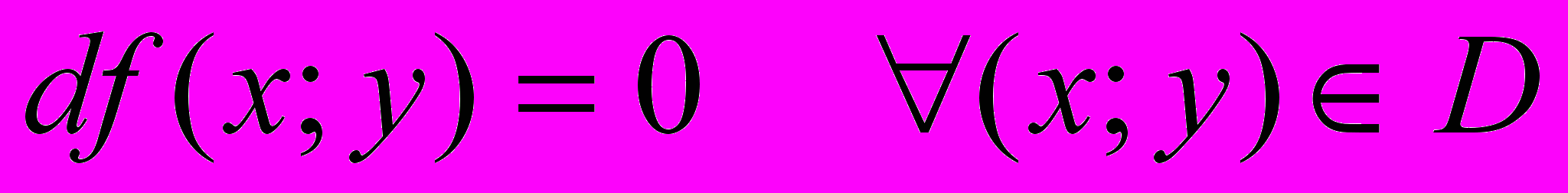

Известно, что 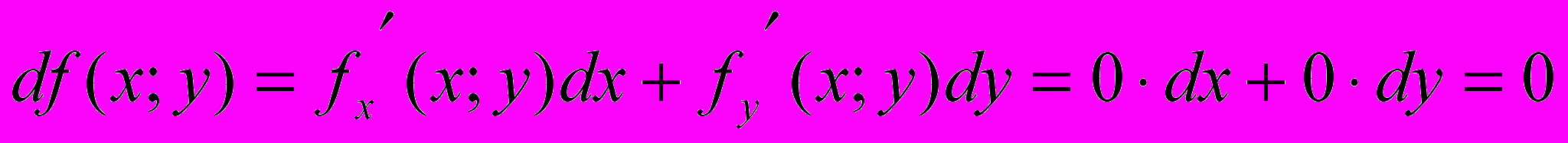. Значит из условия (А) условие (В).

Пусть выполняется условие (В), тогда 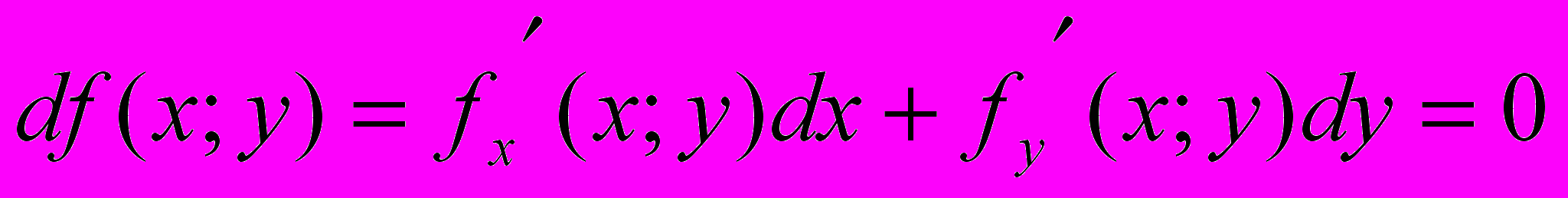.Сначала будем считать, что dy=∆y=0, dx=∆x≠0. Тогда 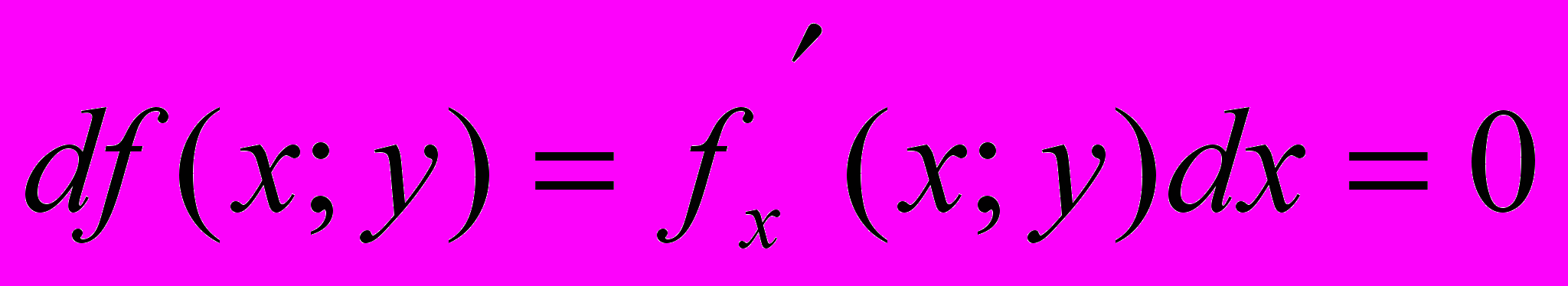, разделим на , dx≠0 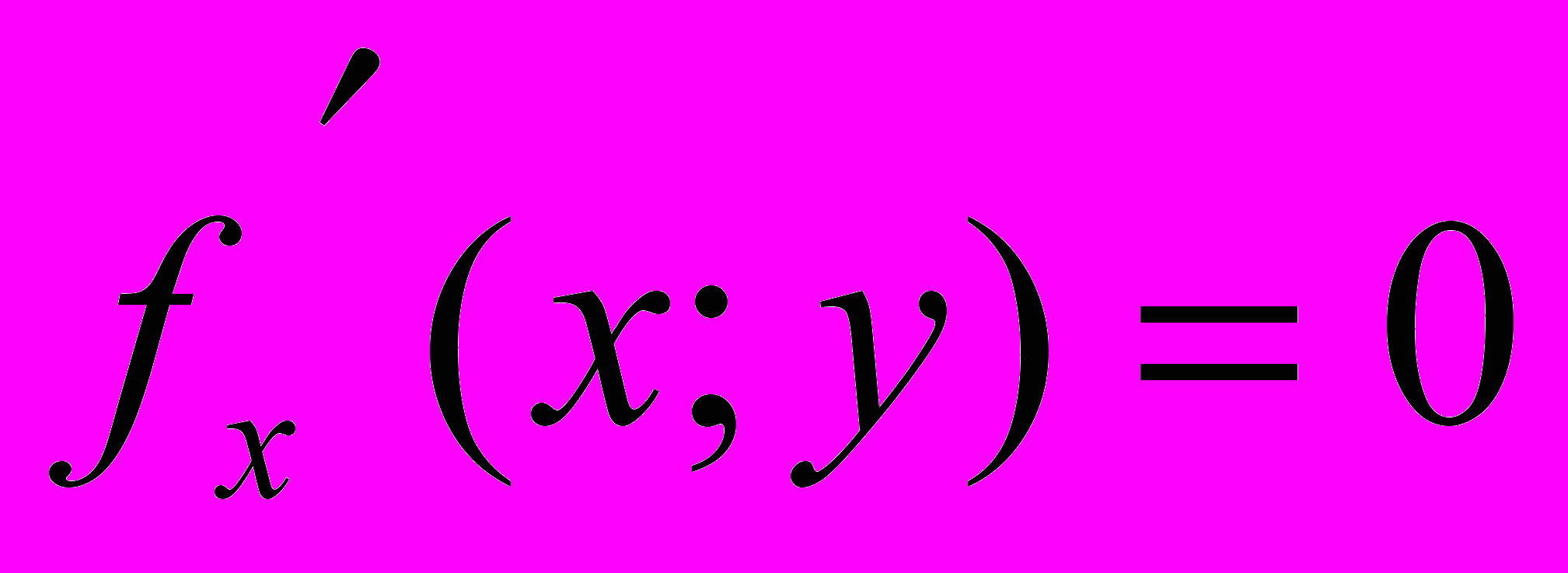. Аналогично доказывается, что .

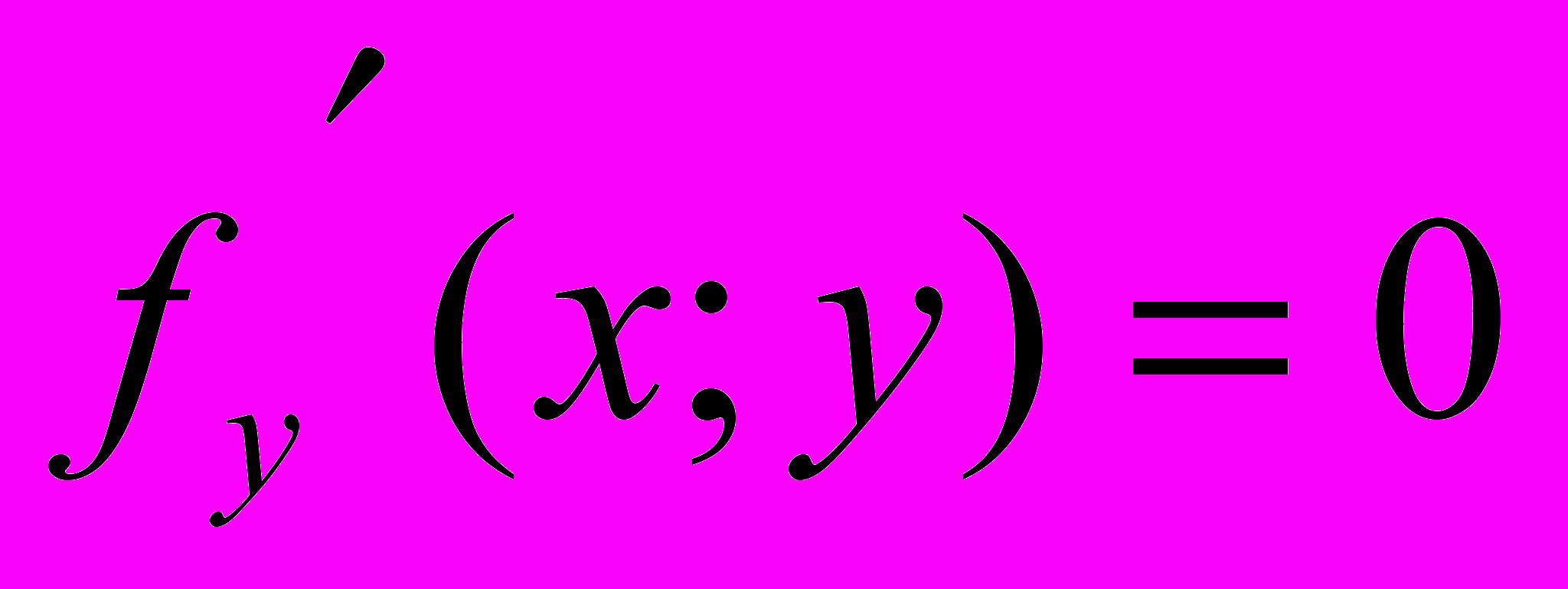Перейдем к доказательству теоремы.

Необходимость. Пусть f(x;y)=c – const 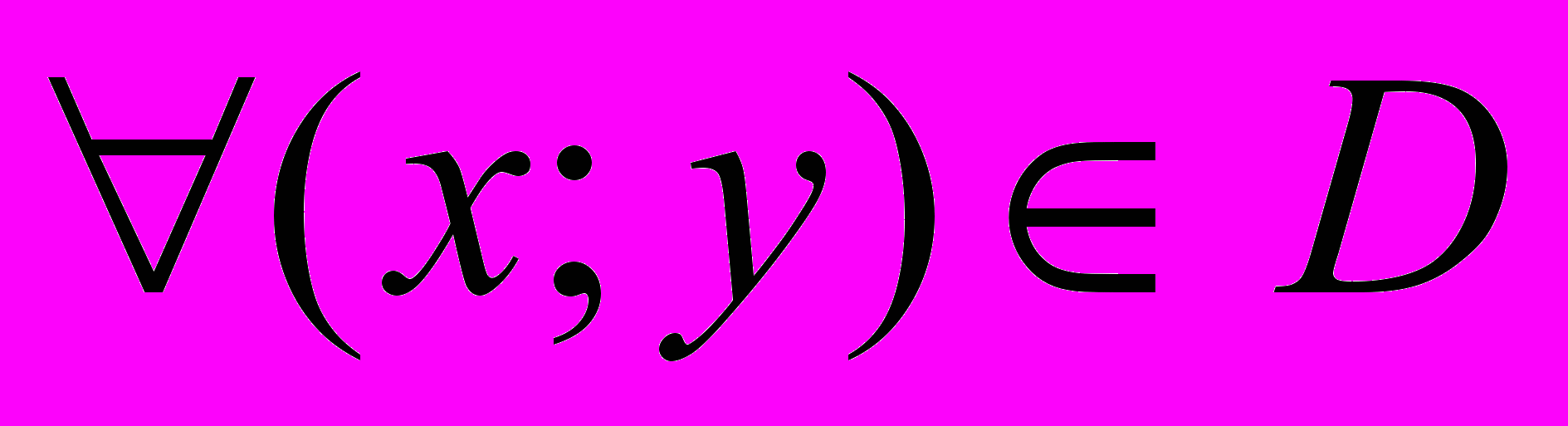тогда будут постоянными функции от одной переменной φ(x)=f(x;y₀) ( y₀ - фиксированное) и ψ(y)=f(x₀;y) (x₀ - фиксированное). Из критерия постоянства функции 1-й переменной получаем φ’(x)=f_x’(x;y)=0 и ψ(y)=f_ý’(x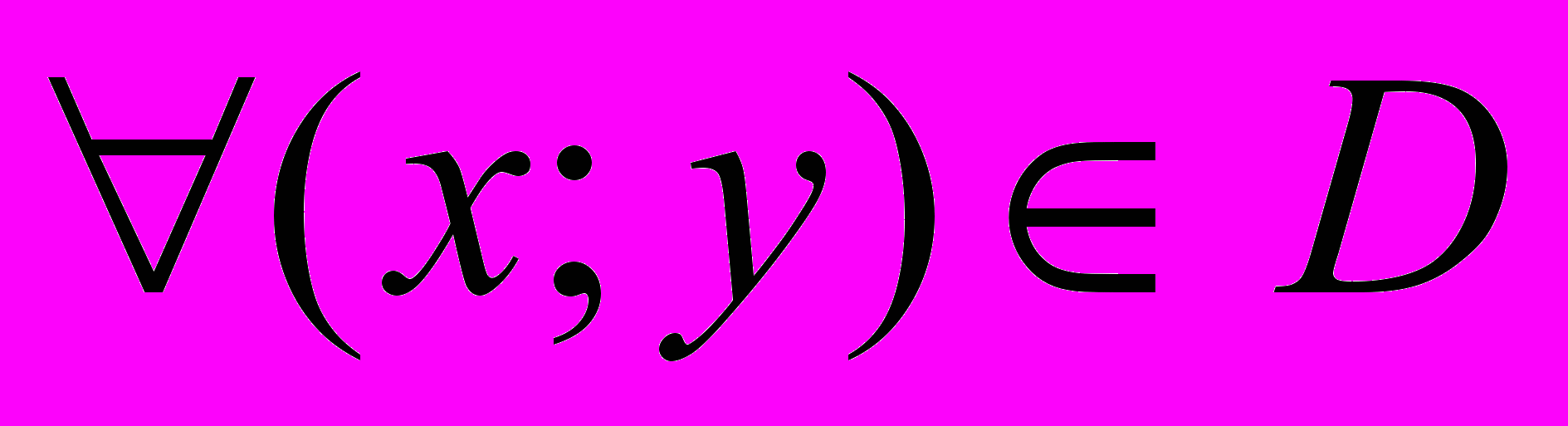,y)=0 df(x;y)=0.

Достаточность. Пусть f_x’(x;y)= f_ý’(x,y)=0 , тогда df(x;y)=0. По условию теоремы f(x;y) дифференцируемая функция в 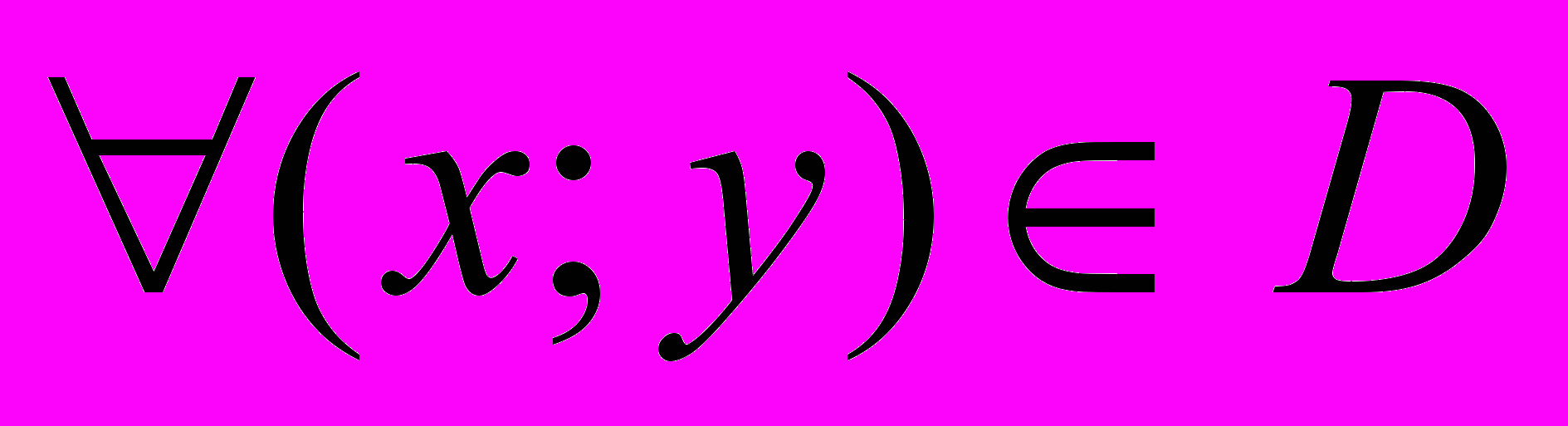, тогда для неё справедлива формула (2). При n=1, формула (2) примет вид ∆f(x₀;y₀)=f(x₀+∆x; y₀+∆y)-f(x;y)=df(x₀+Θ∆x;y₀+ Θ∆y) и точка (x₀+Θ∆x;y₀+ Θ∆y)D, поэтому ∆f(x₀;y₀)=0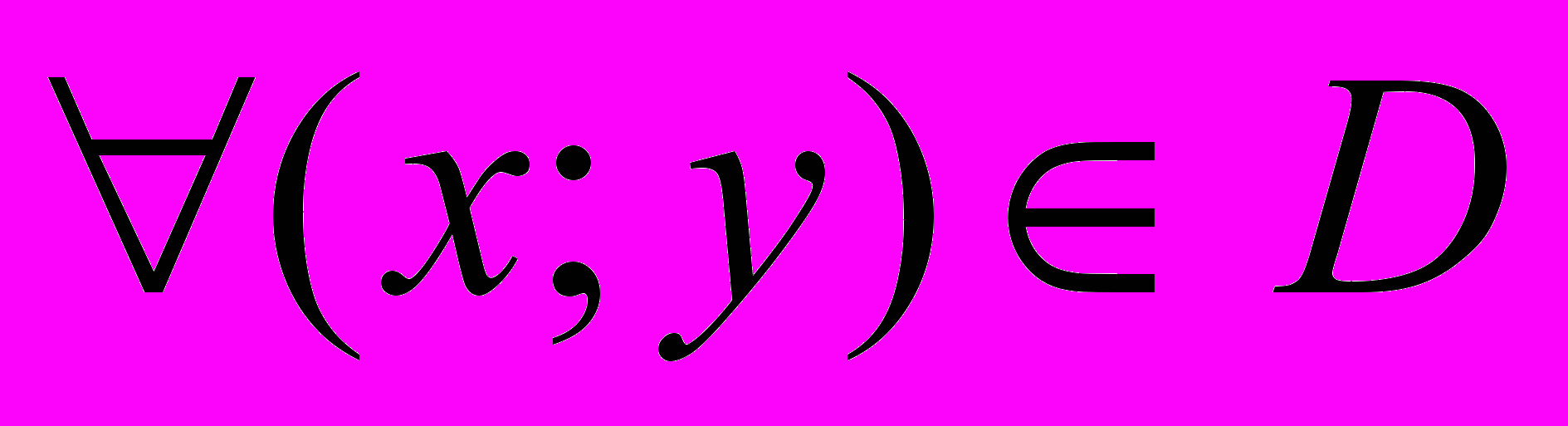 f(x;y) – постоянная.


§ 13. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

п.1. Точки экстремума. Необходимое условие экстремума

Пусть функция z=f(x,y) определена на множестве .

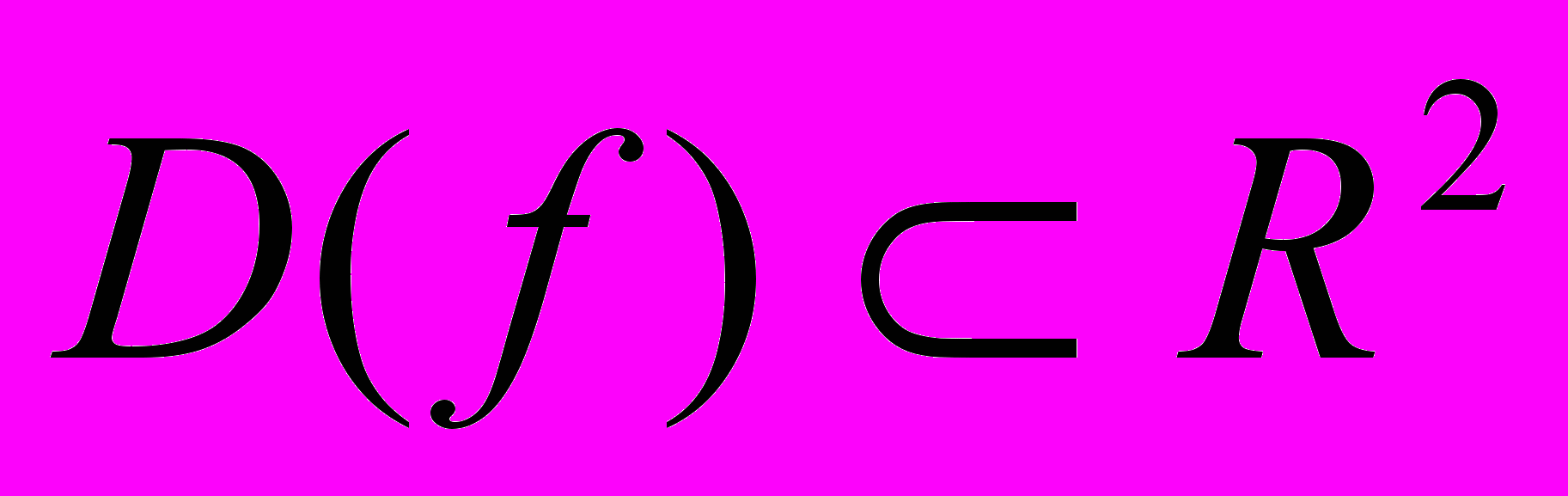Определение 1. Точка 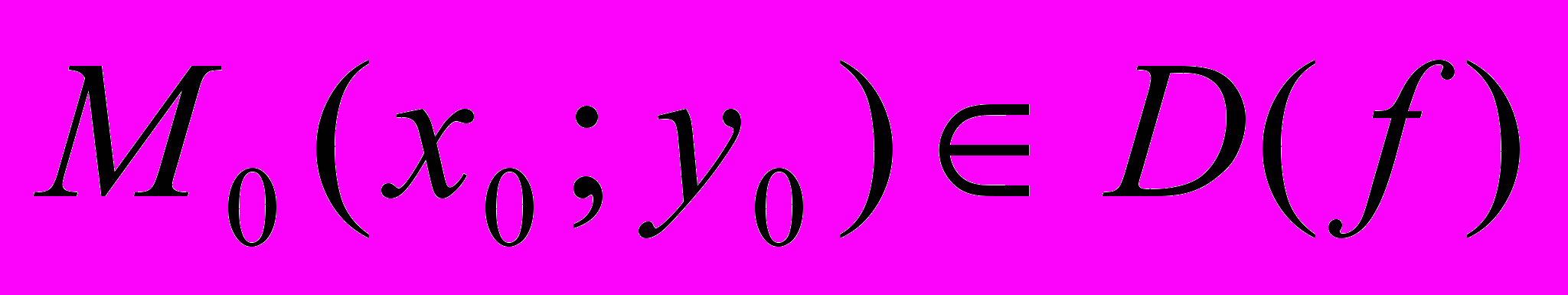называется точкой максимума (минимума) функции f , если существует окрестность точки 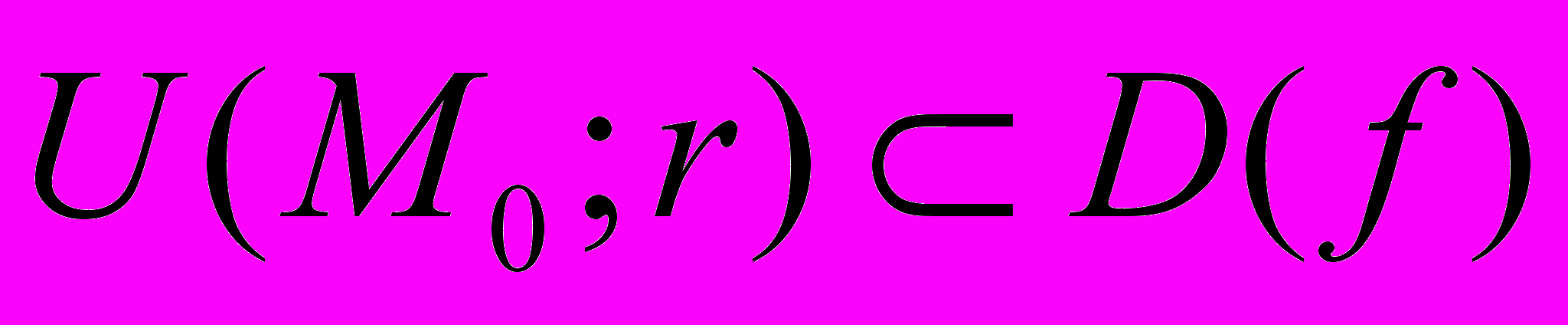такая, что 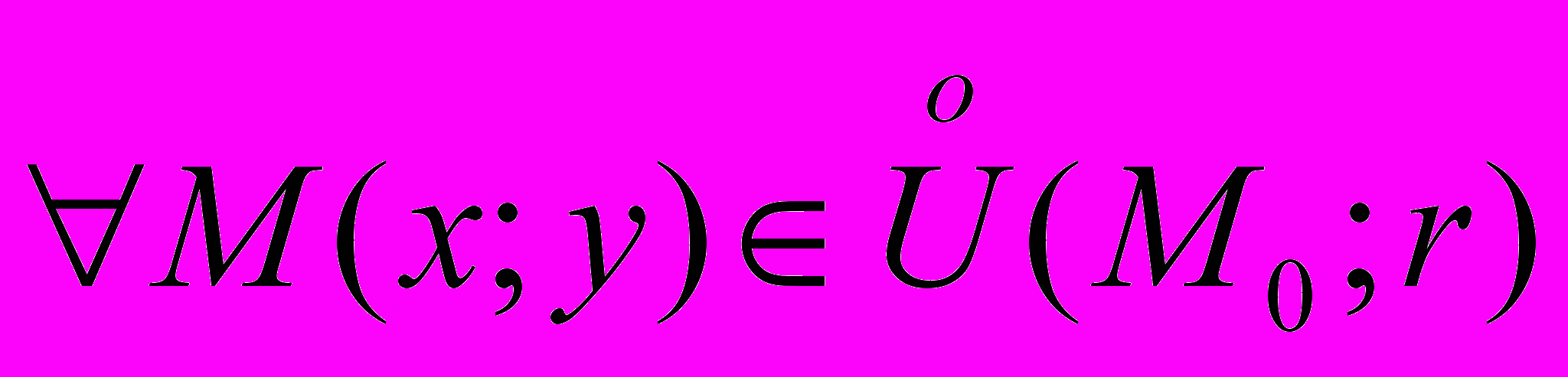выполняется неравенство

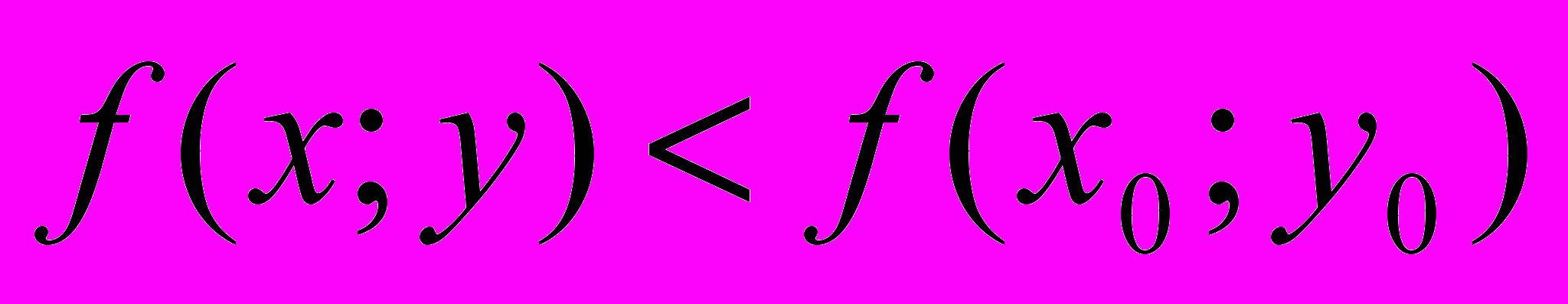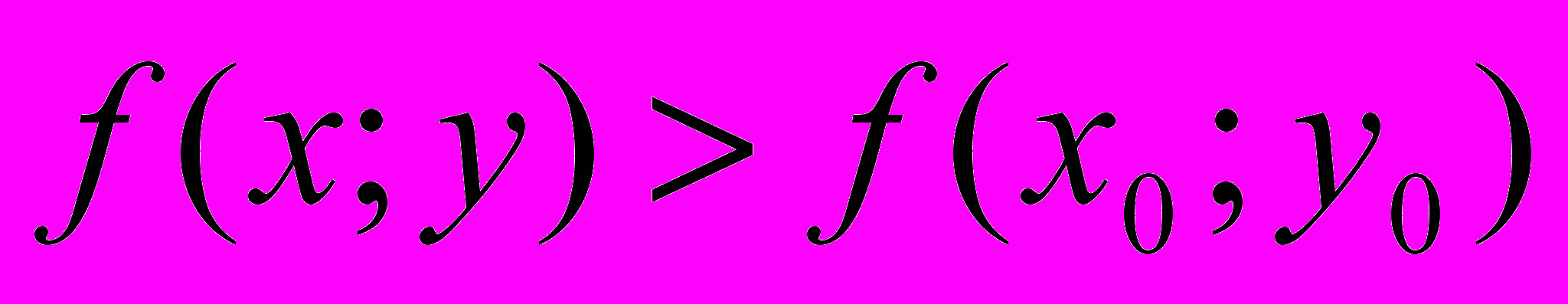(1) () (2)

Точки максимума и минимума называются точками экстремума.

Замечание 1. Неравенство (1) и (2) эквивалентны соответственно неравенствам

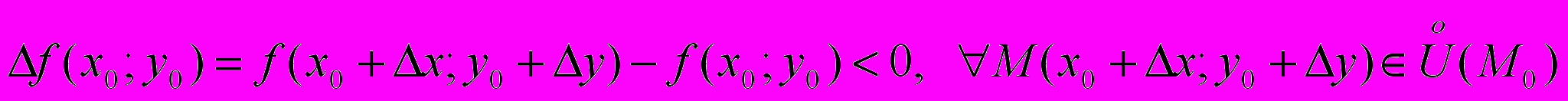(1')

(2')

Пример 1. а) для функции z = x² + y² точка (0;0) – точка минимума.

б) для функции 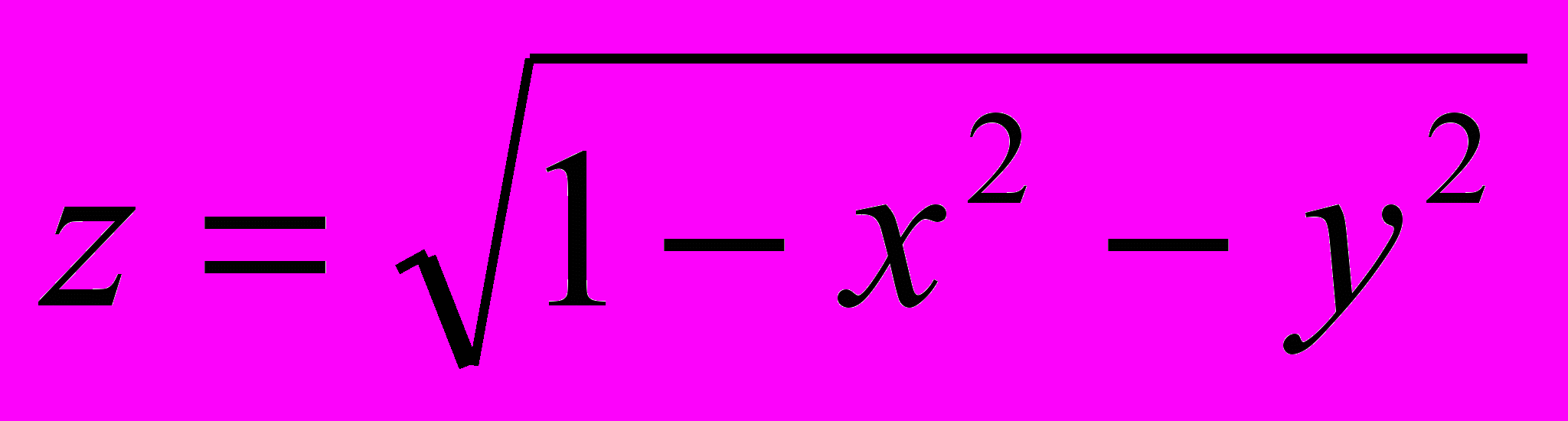точка (0;0) – точка максимума.

Теорема 1. (необходимое условие экстремума)

Если точка 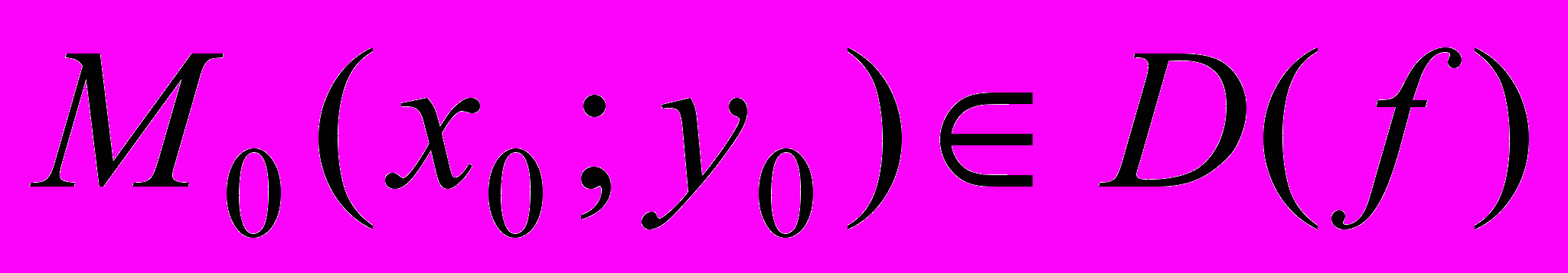является точкой экстремума функции f, и f – дифференцируемая в точке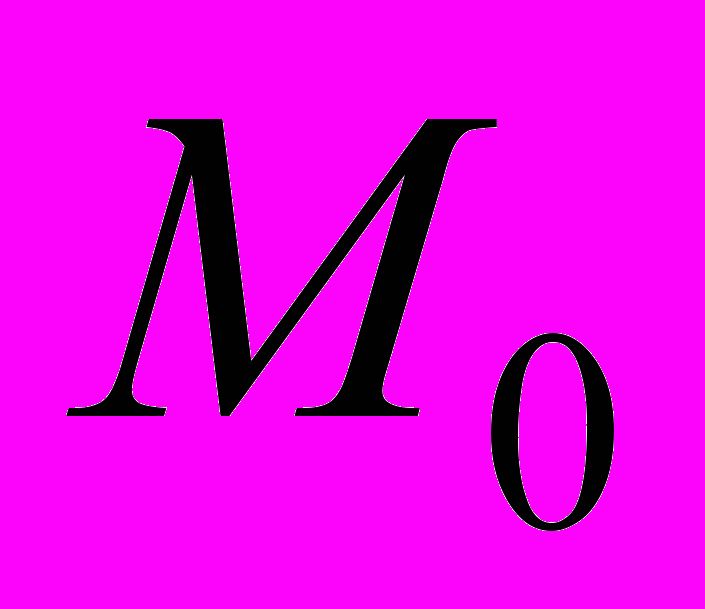, то все частные производные функции f в точке 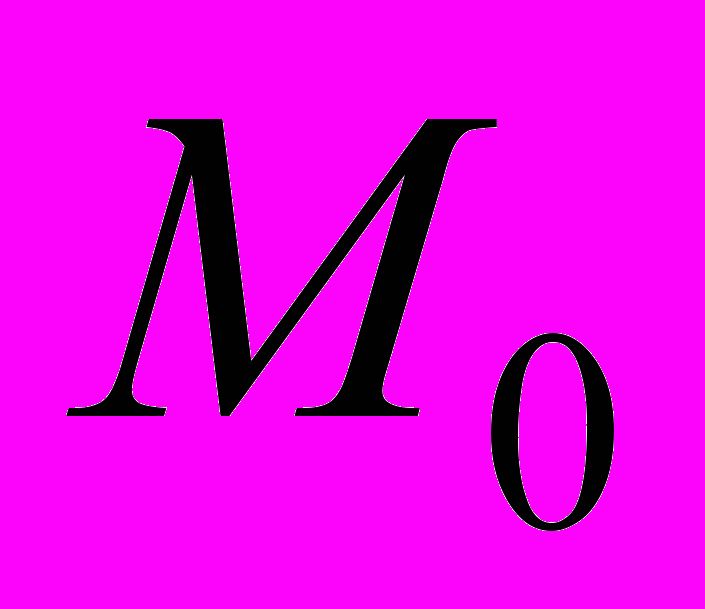равны нулю, т.е. .

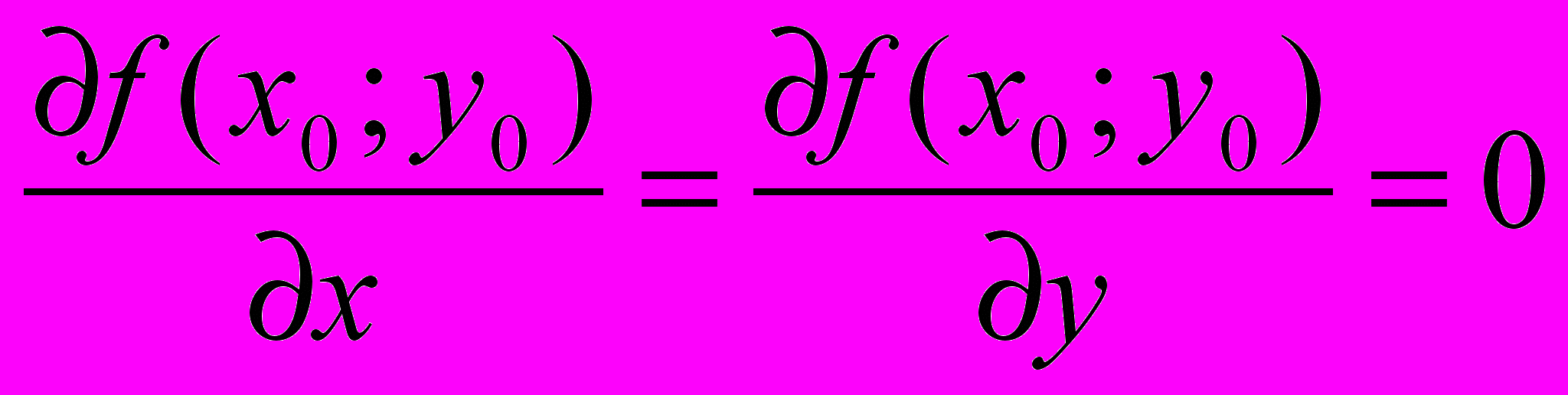Доказательство.


Замечание 2. Необходимое условие не является достаточным условием экстремума.

Пример 2. Для функции 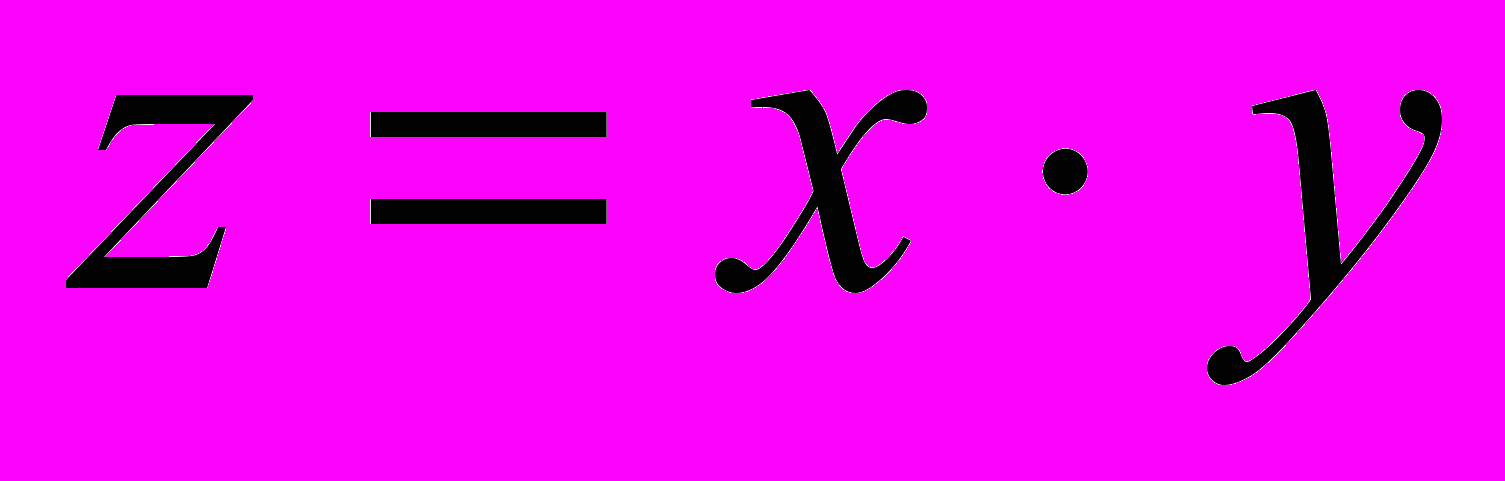частные производные

в точке (0;0) равны 0, но точка (0;0) не является точкой экстремума


Определение 2. Точки, в которых все частные производные равны нулю, называются стационарными точками.

Замечание 3. Точки экстремума будем искать среди стационарных точек и точек, в которых частные производные не существуют.

п.2. Достаточное условие экстремума

Теорема 2. (достаточное условие экстремума)

Пусть точка М₀(х₀,у₀) – стационарная точка функции z = f(x,y) и в некоторой окрестности точки М₀(х₀,у₀) функция f имеет непрерывные частные производные 2-го порядка. Обозначим через A = f' ''_xx (М₀), В = f ''_yy(М₀), C = f ''_xy(М₀), 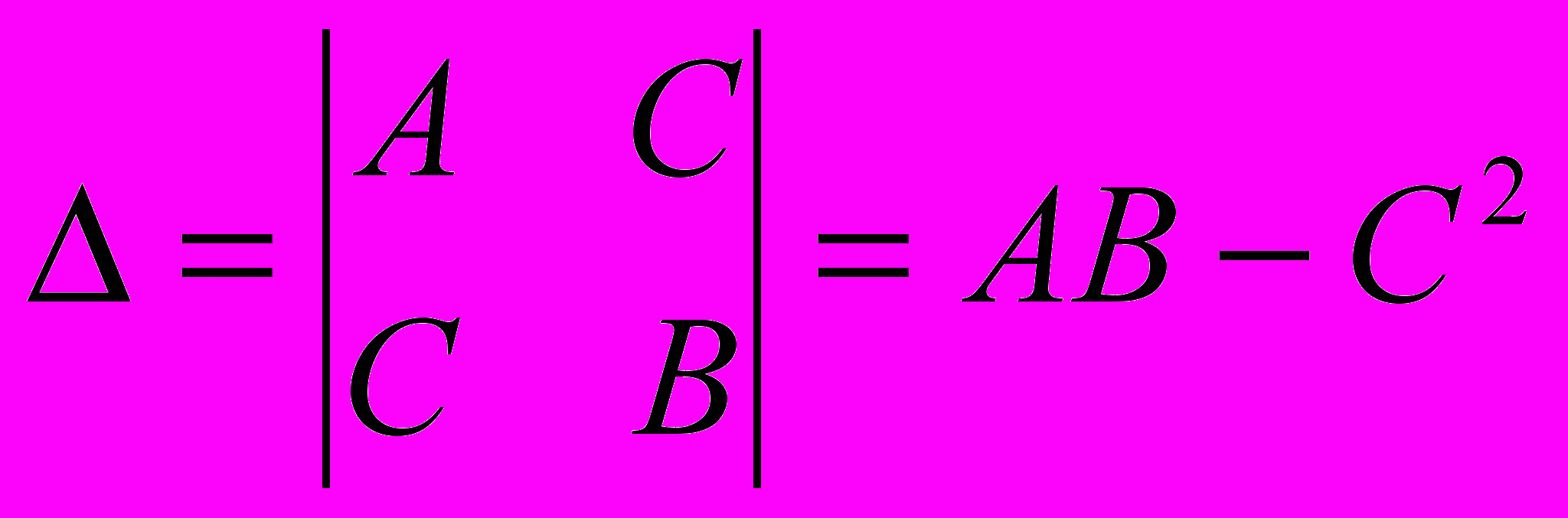. Тогда, если

1. >0, то М₀ – точка экстремума, причем
   

а) при А>0, М₀ – точка минимума;

б) при А<0, М₀ – точка макcимума;

2. <0, то М₀ точкой экстремума не является;
   
3. =0, то М₀ может быть, а может и не быть точкой экстремума, необходимо дополнительное исследование.
   

Доказательство. Так как по условию f(x,y) имеет непрерывные частные производные 2-го порядка в некоторой окрестности точки М₀(х₀,у₀), то f(x,y) – дважды дифференцируемая  справедлива формула Тейлора при п = 1:

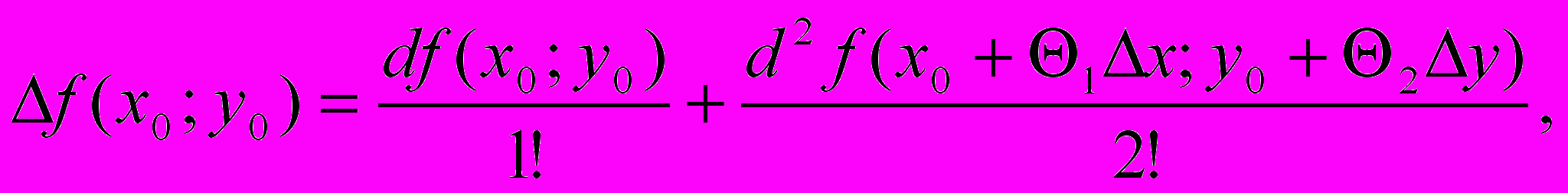(где 0<  <1)

По условию М₀(х₀,у₀) – стационарная точка  d f(x₀,y₀) = 0, поэтому



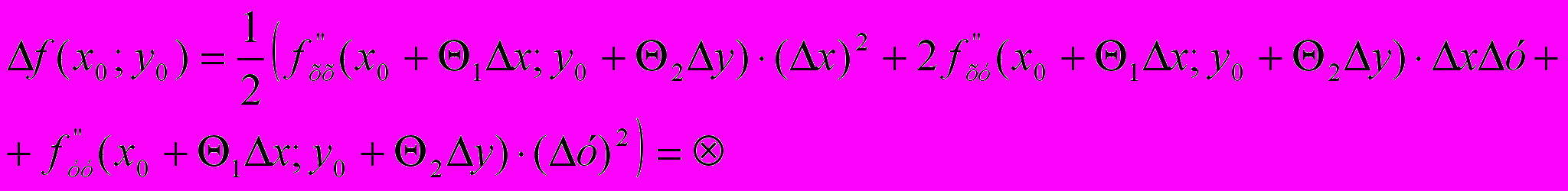
По условию частные производные 2-го порядка – непрерывные функции, тогда в окрестности точки М₀(х₀,у₀) их можно представить в виде



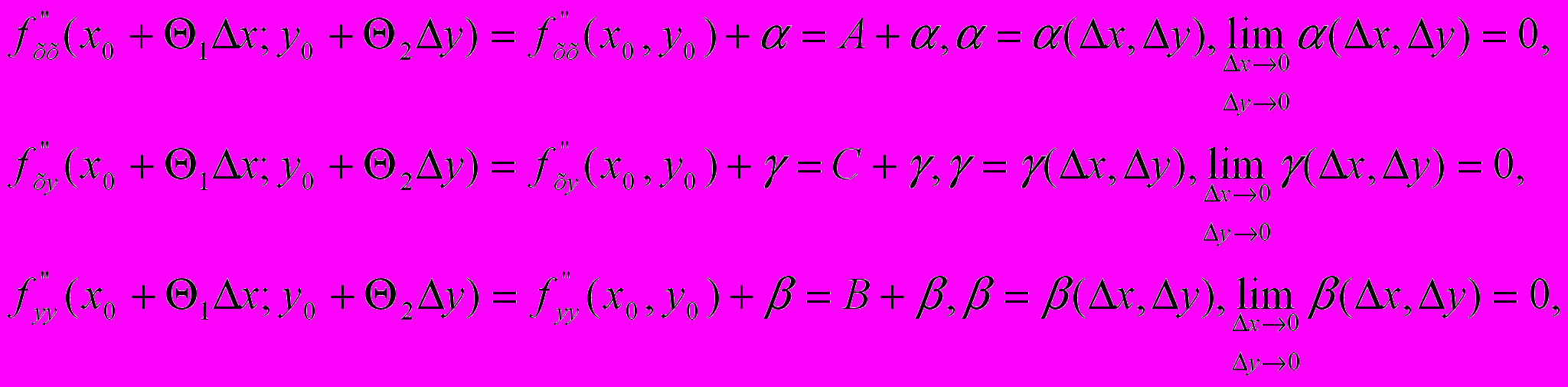
(воспользовались критерием непрерывности функции). Продолжим доказательство

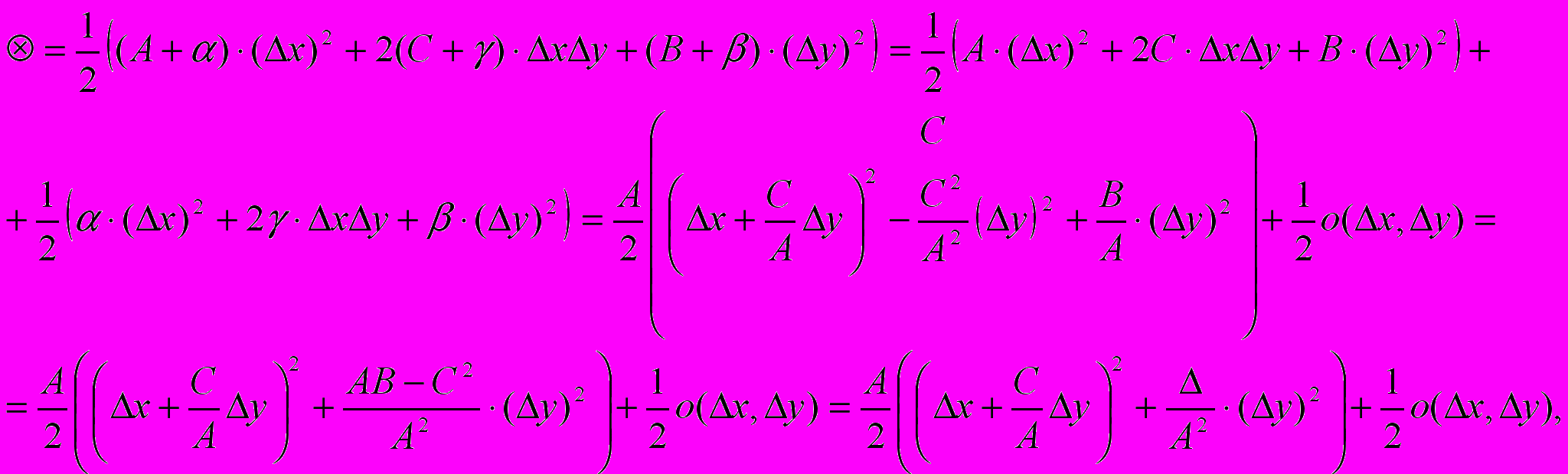где 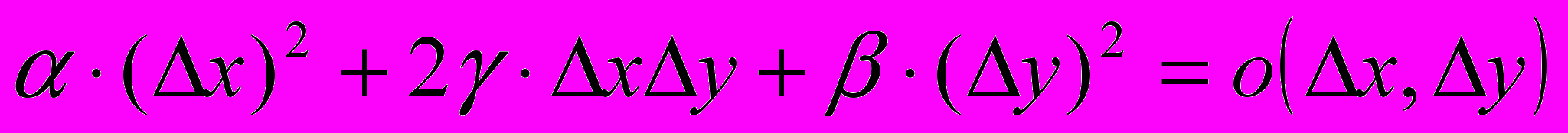– бесконечно малая функция более высокого порядка, чем функция, стоящая в скобках (при 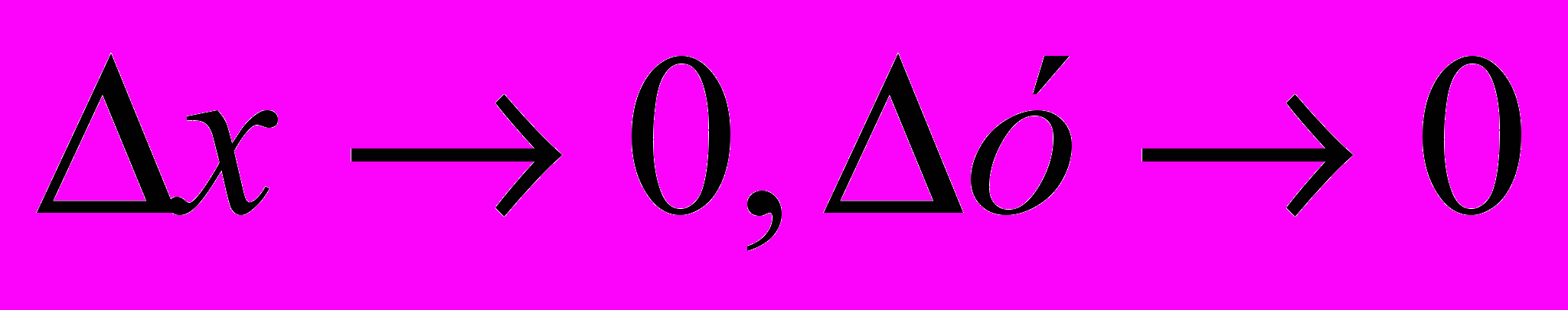). Поэтому знак  f(x₀,y₀) определяется знаком выражения 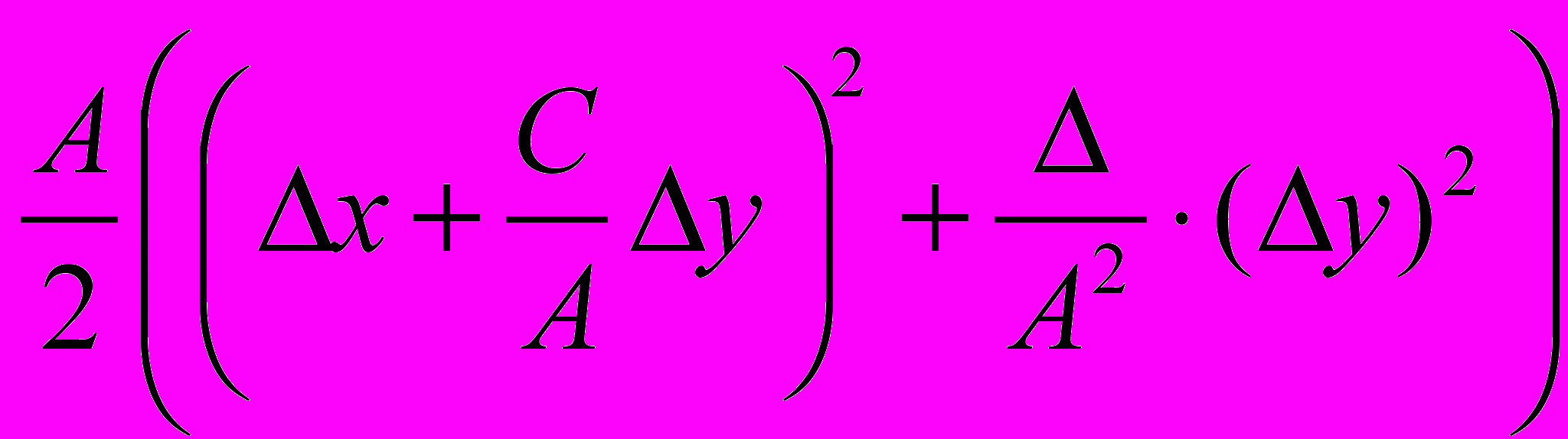. Найдём знак  f(x₀,y₀). Возможны случаи:

1. A>0, AB – C² = >0, то  f(x₀,y₀) > 0  М₀(x₀,y₀) – точка минимума;
   
2. A<0, AB – C² = >0, то  f(x₀,y₀) < 0  М₀(x₀,y₀) – точка максимума;
   
3. AB – C² = <0, то рассматриваемое выражение может быть как положительным, так и отрицательным, всё зависит от х и у   f(x₀,y₀) не имеет конкретного знака в окрестности точки М₀  М₀ точкой экстремума не является;
   
4. AB – C² = =0, то М₀ может быть, а может и не быть точкой экстремума (привести 2 примера, когда М₀ – точка экстремума и когда не является точкой экстремума).
   

п.3. Наибольшее и наименьшее значения функции многих переменных на компакте.

Напомним, что в Rⁿ любое замкнутое ограниченное множество является компактом. Пусть функция z=f(x,y) – непрерывная на компакте . Тогда по II Т. Вейерштрасса она принимает наибольшее и наименьшее значения на К.

Правило нахождения наибольшего и наименьшего значений на компакте К

Найти стационарные точки и точки, в которых не существуют частные производные z'_x , z'_y , принадлежащие К.

Найти значение функции в этих точках.

Найти наибольшее и наименьшее значения функции на границе компакта К.

Выбрать наибольшее и наименьшее значения среди значений пунктов 2 и 3.

п.4. Условный экстремум. Метод Лагранжа

Пусть функция z = f(x,y) определена на множестве X . Рассмотрим точки из множества X, удовлетворяющие дополнительному условию F(x;y;)=0, они образуют множество Е. Уравнение

F(x;y;)=0 (3)

называют уравнением связи. Точка М₀(x₀,y₀) называется точкой условного экстремума функции z = f(x,y) относительно уравнений связи (3), если она является точкой обычного экстремума функции z = f(x,y) на множестве E.

Возможны случаи:

1. Из уравнения (3) можно выразить явно y через x, т.е. y =g(x). Тогда нахождение условного экстремума сводится к нахождению экстремума функции z = f(x,y) = f(x, g(x)).

2. Из уравнения (3) нельзя выразить явно y через x., т.е. (3) задаёт неявно функцию y=y(x). В этом случае будем находить точки условного экстремума с помощью метода Лагранжа, т.е. используя

Теорема 3. (Необходимое условие условного экстремума)

Если точка М₀(x₀,y₀) – точка условного экстремума функции z = f(x,y) относительно уравнений связи (3), то найдется такое действительное число λR, что

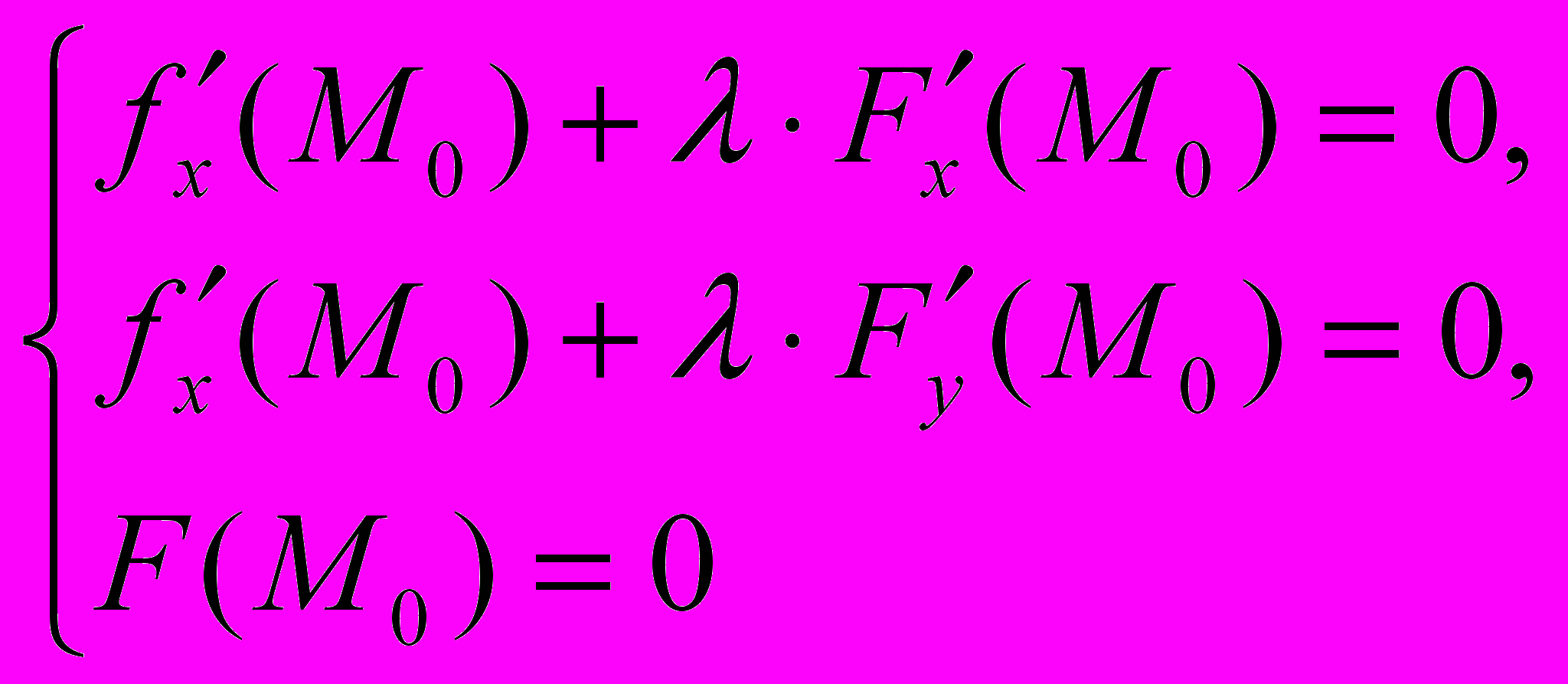(4)

Доказательство. Т.к. (3) задаёт неявно функцию y=y(x), то (по необходимому условию экстремума) в точке (x₀,y₀): 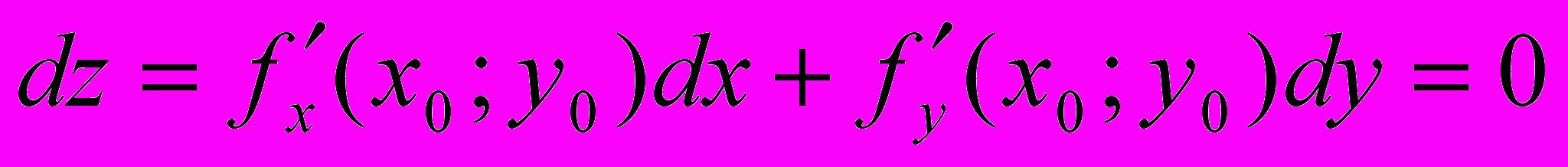, (5)

где dx – приращение аргумента, а dy – дифференциал неявной функции y=y(x). Подставим в уравнение связи (3) вместо y значение y(x), получим тождество F(x;y(х))0. Продифференцируем его и подставим x₀,y₀: 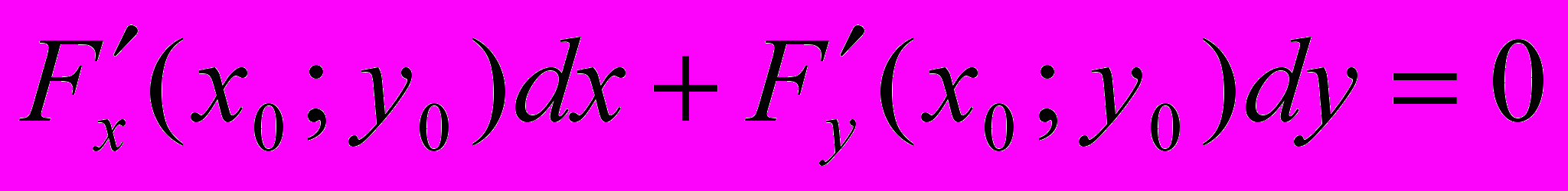. Умножим на λ и прибавим к (5):

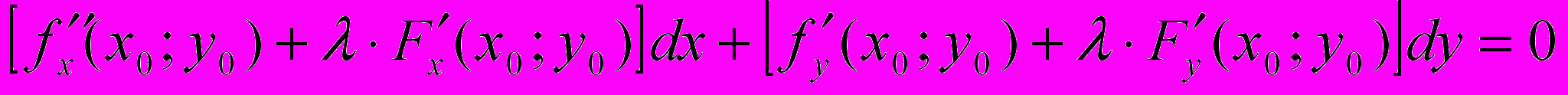. (6)

Выберем λ таким, чтобы 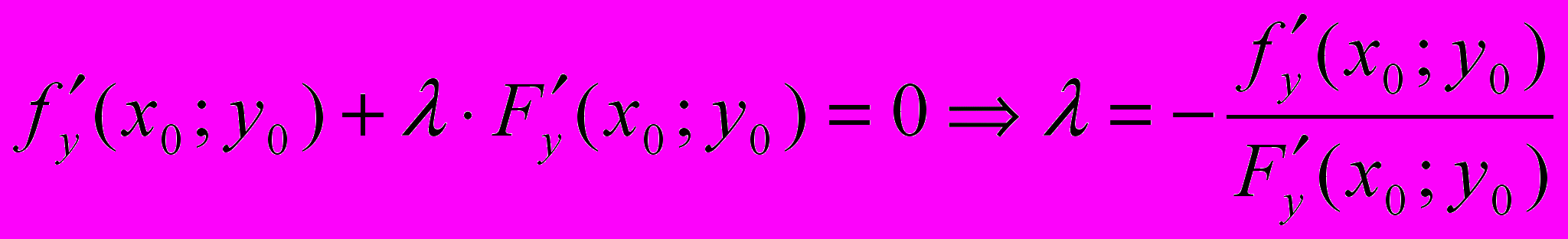. Тогда (6) верно для любых dx и dy , если выполняются два первых уравнения системы (4). Т.к. (x₀,y₀) удовлетворяют уравнению связи (3), то должно выполняться и третье уравнение системы (4). Т. о. получаем систему 3-х уравнений (4) с 3-мя неизвестными x, y,λ, её решение (x₀,y₀, λ₀), где λ₀ – вспомогательная величина , а пара (x₀,y₀) – координаты точки условного экстремума.

Замечание 4. Вместо системы (4) часто используют вспомогательную функцию Лагранжа

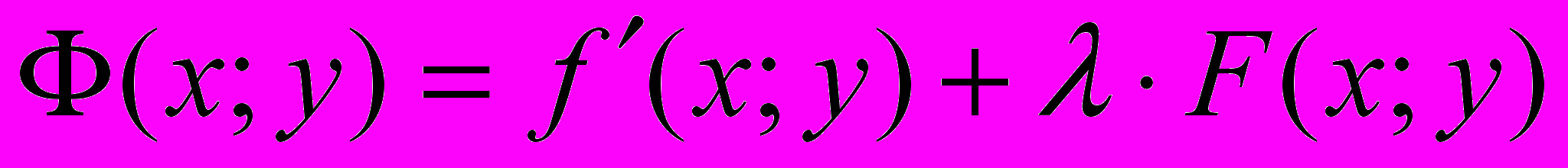(7)

Требуем, чтобы все частные производные (7) были равны нулю.

Замечание 5. Решение системы (4) – точки подозрительные на условный экстремум. Чтобы выяснить вопрос о существовании и характере экстремума, будем изучать знак 2-го дифференциала. Если

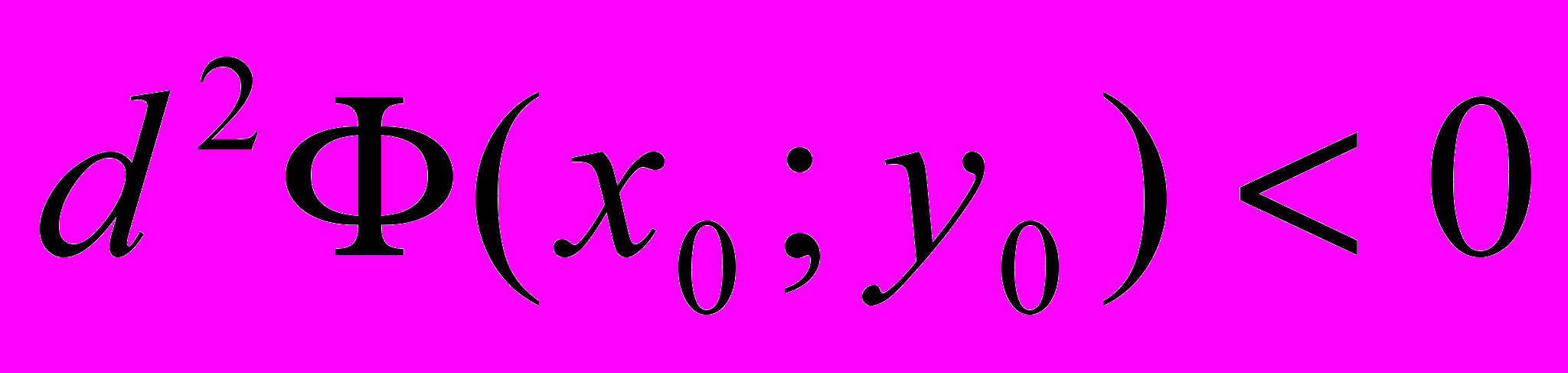, то (x₀,y₀) –точка условного максимума;

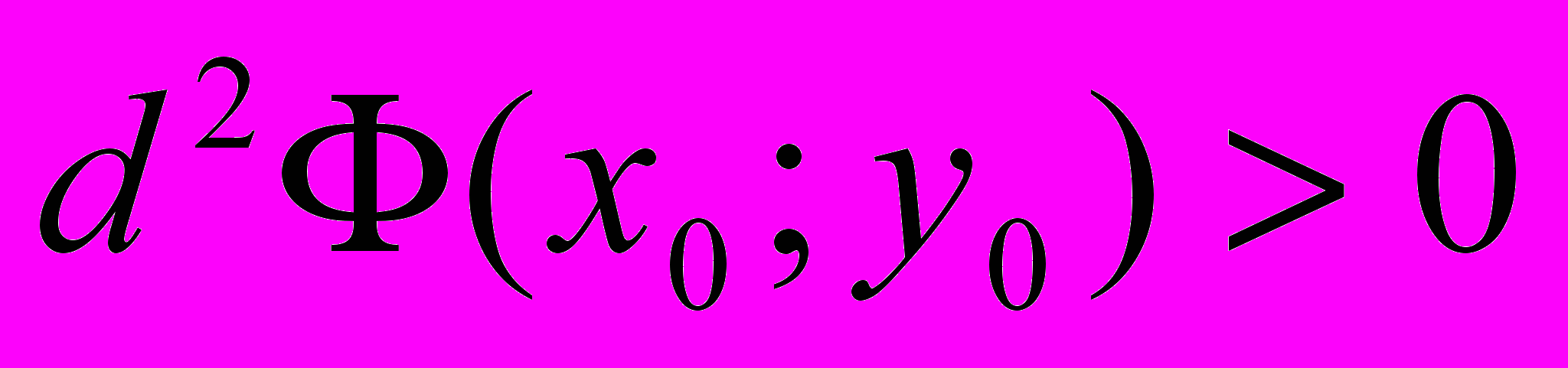, то (x₀,y₀) –точка условного минимума.

Пример 3. Найти условный экстремум функции 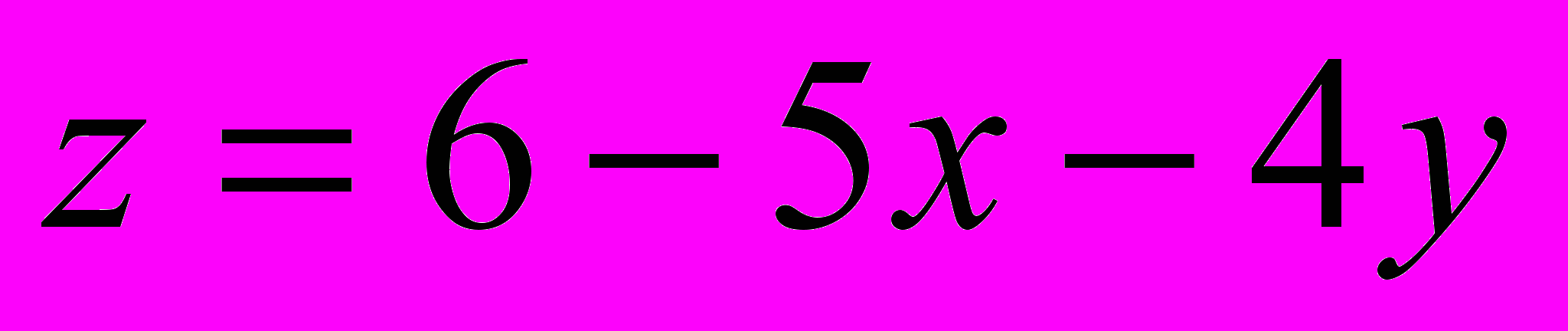относительно уравнения связи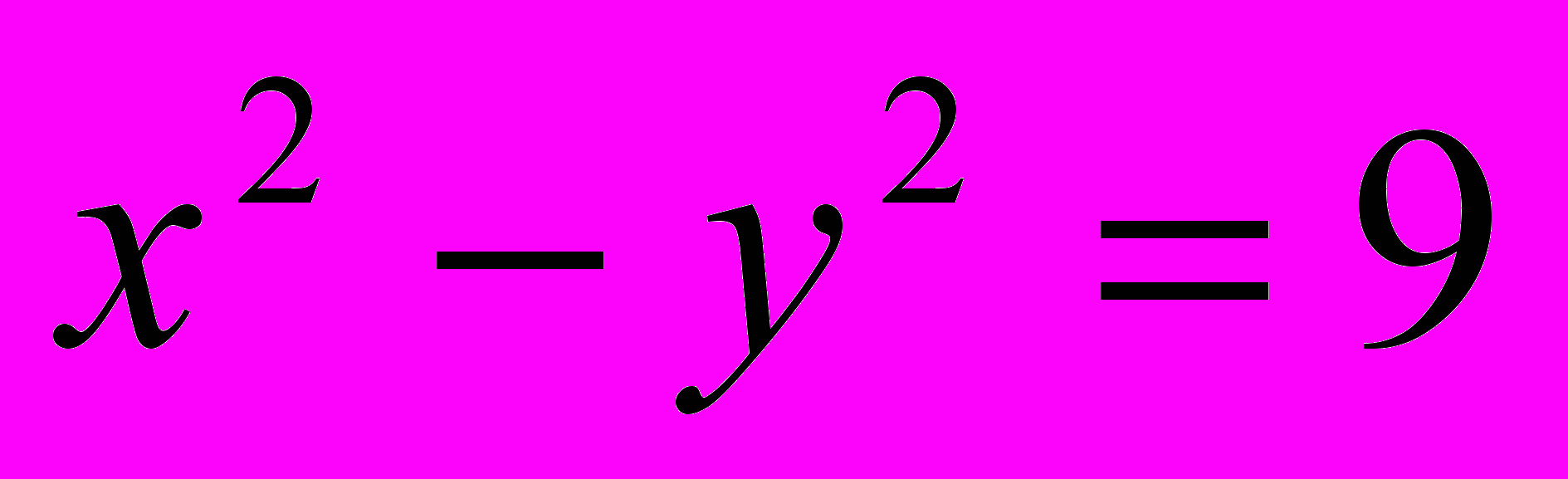

Решение.