Geum.ru

Программа-минимум кандидатского экзамена по специальности 01. 01. 01- математический анализ

Вид материалаПрограмма-минимум
Подобный материал:

ПРОГРАММА-МИНИМУМ

кандидатского экзамена по специальности

01.01.01- Математический анализ


Анализ I II (Математический анализ)

  1. Верхний и нижний пределы последовательности.
  2. Дифференцируемость в точке функции f: Rn Rm. Дифференциал и частные производные. Достаточные условия дифференцируемости.
  3. Кривая и критерий спрямляемости кривой. Длина непрерывно дифференцируемой кривой.
  4. Теорема существования и дифференцируемости неявной функции (F(x,y)=0, F: Rn Rm  Rm).
  5. Условный экстремум. Метод множителей Лагранжа.
  6. Почленное дифференцирование на отрезке функционального ряда.
  7. Формула замены переменных в кратном интеграле Римана (общая схема)


Анализ III (Мера и интеграл Лебега. Функциональный анализ)

  1. Теорема Кантора-Бернштейна. Сравнение мощностей любых множеств. Существование множества мощности большей, чем мощность данного множества.
  2. Продолжение мера с полукольца на порожденное им кольцо, с сохранением при этом -аддитивности.
  3. Лебегово продолжение меры, заданной на полукольце.
  4. Измеримые функции и действия над ними.
  5. Теорема Егорова.
  6. Теорема Лебега о сходимости по мере, сходящейся почти всюду последовательности.
  7. Теорема Ф. Рисса о сходимости почти всюду подпоследовательности сходящейся по мере последовательности.
  8. Теорема Лузина.
  9. Определение и основные свойства интеграла Лебега (аддитивность, монотонность, эквивалентность интегрируемости и абсолютной интегрируемости). Сравнение интеграла Лебега с интегралом Римана.
  10. Интегрируемость на ограниченном измеримом множестве ограниченной измеримой функции. Счетная аддитивность интеграла Лебега.
  11. Абсолютная непрерывность интеграла Лебега.
  12. Теорема Лебега о предельном переходе под знаком интеграла.
  13. Теорема Беппо-Леви.
  14. Лемма Фату.
  15. Произведение мер. Теорема Фубини.
  16. Функции с ограниченным изменением.
  17. Теорема Лебега о дифференцируемости монотонной функции.
  18. «Малая теорема Фубини».
  19. Производная неопределенного интеграла Лебега.
  20. Абсолютно непрерывные функции.
  21. Теорема Лебега о восстановление абсолютно непрерывной функции по её производной.
  22. Теорема Радона-Никодима.
  23. Интеграл Римана-Стильтьеса и интеграл Лебега-Стильтьеса.
  24. Банахово пространство Lp(a,b) (1p<).
  25. Банахово пространство существенно ограниченных измеримых функций L (a,b).
  26. Теорема о пополнении метрических пространств.
  27. Теорема Бэра-Хаусдорфа о категориях. Применение к существованию нигде не дифференцируемой непрерывной функции.
  28. Компактные, счетно-компактные, секвенциально -компактные, предкомпактные пространства. Компактное пространство, как пространство с непустым пересечением каждой замкнутой.
  29. Основная теорема о компактности метрических пространств(Теорема об эквивалентности, компактности, счётной компактности, секвенциальной компактности, полноты и полной ограниченности метрических пространств).
  30. Критерий предкомпактности множеств в полном метрическом пространстве. Теорема Арцела.
  31. Компактность ограниченных множеств, как характеристическое свойство конечномерности нормированного пространства.
  32. Топологические пространства. Различные способы задания топологии в пространстве.
  33. Полнота пространства линейных ограниченных операторов ζ(NB) относительно сходимости по норме.

Функциональный анализ
  1. Принцип равномерной ограниченности (теорема Банаха-Штейнгауза).
  2. Теорема Банаха об обратном операторе. Принцип открытости отображения.
  3. Теорема Банаха о замкнутом графике.
  4. Принцип продолжения Хана-Банаха.
  5. Полнота пространств линейных ограниченных операторов ζ(BB) относительно поточечной сходимости. Критерий поточечной сходимости АnA.
  6. Общий вид линейных функционалов в С[0,1] (теорема Ф. Рисса).
  7. Общий вид линейных функционалов в Lp(0,1).
  8. Общий вид линейных функционалов в гильбертовом пространстве (теорема Ф. Рисса).
  9. Сопряженные пространства. Рефлексивные пространства. С[0,1] как пример нерефлексивные пространства.
  10. Слабая сходимость и слабая топология в нормированном пространстве. Единственность слабого предела. Ограниченность норм слабо сходящейся последовательности.
  11. Слабая топология и слабая сходимость в сопряженном пространстве.
  12. Слабая компактность шара из пространства, сопряженное к сепарабельному.
  13. Ортогональные разложения в гильбертовом пространстве.
  14. Базисы в гильбертовом пространстве, ортогонализация. Полнота и замкнутость.
  15. Теорема Рисса-Фишера. Теорема об изоморфизме сепарабельных гильбертовых пространств.
  16. Ортогональные системы функций в L2. Условие Дини сходимости тригонометрического ряда Фурье-Лебега в точке.
  17. Интегральная формула Фурье. Преобразование Фурье и формула обращения. Условие Дини.
  18. Обобщенные функции. Дифференциальные уравнения с обобщенными функциями.
  19. Вполне непрерывные операторы.
  20. Абсолютная норма оператора. Класс Шмидта. Интегральные операторы Гильберта-Шмидта.
  21. Альтернатива Фредгольма.
  22. Проектирующие операторы. Свойства.
  23. Спектр оператора. Резольвента.
  24. Симметрические операторы (действительность собственных значений, ортогональность собственных элементов, отношение порядка между симметрическими операторами, существование предела монотонной последовательности).
  25. Спектральная теорема для симметрического вполне непрерывного оператора.
  26. Спектральная теорема для симметрического ограниченного оператора.
  27. Спектральная теорема для унитарного оператора.
  28. Спектр симметрического ограниченного оператора.
  29. Спектр и резольвента неограниченных операторов.


Анализ IV (Теория функций комплексного переменного)

  1. Пути и кривые. Основные свойства: Жордановые, непрерывно-дифференцируемые, гладкие, спрямляемые. Достаточное условие спрямляемости кривой.
  2. Области. Лемма о том, что любые две точки области можно соединить ломанной. Теорема Жордана (без доказательства). Классификация областей на основе теоремы Жордана.
  3. Дифференцируемость комплекснозначной функции. Условие Коши-Римана. Аналитические функции.
  4. Интеграл. Основные свойства интеграла: линейность, инвариантность относительно замены параметра, ориентированность, оценка интеграла и почленное интегрирование функциональных рядов.
  5. Теорема Коши для односвязной области. Обобщение теоремы Коши на случай не односвязных областей.
  6. Интегральная теорема Коши. Следствия: теорема о среднем.
  7. Теорема о представлении голоморфных функций в виде степенного ряда(Тейлора). Следствия: неравенство для коэффициентов ряда Тейлора, теорема Лиувилля.
  8. Степенной ряд. Формула Коши-Адамара. Голоморфность суммы степенного ряда в круге его сходимости.
  9. Гомоморфность производной голоморфной функции. Следствия: бесконечная дифференцируемость голоморфной функции, формулы для коэффициентов ряда Тейлора(через производную и через интеграл).
  10. Теорема Морера. Три эквивалентных определения голоморфных функций.
  11. Теорема единственности
  12. Теорема Вейерштрасса о почленном дифференцировании рядов.
  13. Ряды Лорана.Изолированные особые точки и их классификация на основе рядов Лорана.
  14. Вычеты. Теорема Коши о вычетах, вычисление вычетов в полюсах, применение вычетов к вычислению интегралов.
  15. Аналитический элемент. Продолжение аналитических элементов. Конкретизация продолжения. Продолжение вдоль пути.
  16. Аналитическая функция, ветви аналитической функции. Равенство аналитических функций и действия над аналитическими функциями. Выделение ветвей аналитических функций. Выделение ветвей аналитических функций.
  17. Принцип аргумента. Следствие: теорема Рунге, основная теорема алгебры.
  18. Принцип максимума модуля и лемма Шварца.
  19. Конформное отображение. Конформное отображение элементарными функциями



Литература




  1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа.
  2. Иосида К., Функциональный анализ.
  3. Садовничий В.А., Теория операторов.
  4. Люстерник Л.А., Соболев В.И., Элементы функционального анализа.
  5. Натансон И.П., Теория функций вещественной переменной.
  6. Рудин У., Основы математического анализа.
  7. Шабат, «Теория функций комплексного переменного».
  8. Маркушевич А.И. Курс аналитических функций. Том 1,2.
  9. Дьяченко М.И., Ульянов П.Л. Мера и интеграл. М., 1998.


Дополнительные вопросы

к кандидатскому минимуму по специальности 01.01.01 –

математический анализ

  1. Существование в любом банаховом пространстве функции с наперед заданной произвольной последовательностью наилучших приближений относительно замкнутой счетной системы [1, стр.50-53].
  2. Прямые (типа Джексона [2, стр.287-292], [3, стр.117]) и обратные (типа Бернштейна [2, стр.344-346]) теоремы теории приближений (в разных метриках соответственно [4]) относительно тригонометрической системы. Теорема Зигмунда ([2, стр.142], [1, стр.346], [3, стр.883]).
  3. Пространства функций с доминирующей смешанной производной Никольского-Бесова-Аманова: эквивалентные нормировки и теоремы вложения. Теоремы вложения Т.И.Аманова [4, 11].
  4. Обобщенные производные в смысле Соболева. Пространства Соболева ([5]). Теоремы вложения Соболева ([5]).
  5. Интерполяционные теоремы Рисса-Торина, Марцинкевича ([6,7]).
  6. Максимальная функция Харди-Литтлвуда ([6,7]).
  7. Тригонометрическая система: ядра Дирихле, оценки коэффициентов Фурье через интегральный модуль непрерывности [8, стр.124-129]. Небазисность тригонометрической системы в С 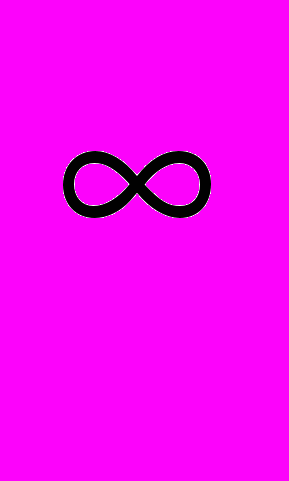= Lи L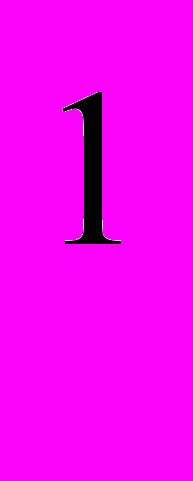. Средние Фейера и средние Валле-Пуссена [8, стр.129-136]. Сходимость тригонометрических рядов в L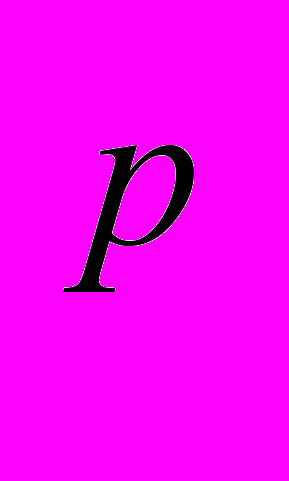(1
    ) - теорема М. Рисса ([8]).
  8. Система Хаара. Теорема о равномерной сходимости ряда Фурье-Хаара непрерывной функции к ней самой [8, стр.76-82].
  9. Система Уолша, свойства. Ядро Дирихле по системе Уолша. Свойства частичных сумм ряда Фурье-Уолша ([8])

.
  1. О дискретности спектра полуограниченного оператора Штурма-Лиувилля ([10]).



Л И Т Е Р А Т У Р А
  1. Тиман А.Ф. Теория приближений функций действительного переменного. М.: Физматгиз, 1960.
  2. Натансон И.П. Конструктивная теория функций. М.: Гостехиздат, 1949.

3. Бари Н.К. Тригонометрические ряды. М.: ФМ, 1961.
  1. Аманов Т.И. Пространства дифференцируемых функций с доминирующей смешанной производной. Алма-Ата:

Fылым, 1976.
  1. Соболев С.Л., Некоторые применения функционального анализа в математической физике. Ленинград: изд. ЛГУ,1950г (Новосибирск, 1962).
  1. Берг Й., Лефстрем И. Интерполяционные пространства. М.:Мир, 1980.
  2. СтейнИ., Вейс Г. Введение в гармонический анализ на евклидовых пространствах. М. Мир, 1974.
  3. Кашин Б.С., Саакян А.А. Ортогональные ряды. М.: Наука, 1981.
  4. Мынбаев К.Т., Отелбаев М.О. Весовые функциональные пространства и спектр дифференциальных операторов. М., Наука, 1988.
  5. Отелбаев М.О. Оценки спектра оператора Штурма-Лиувилля. Алма-Ата, Fылым, 1990.
  6. Никольский С.М. Приближение функций многих переменных и теорема вложения. М.: Наука, 1969 (в 1977 году вышло 2-е издание).



программа – минимум


кандидатского экзамена

по специальности 01.01.02 – дифференциальные уравнения

и математическая физика


  1. Теоремы существования и единственности решения задачи Коши для линейных и нелинейных систем первого порядка ([1], § 3, 21).
  2. Линейные уравнения и системы с постоянными коэффициентами и специальными правыми частями ([1], § 7,8,10,12,14).
  3. Линейные уравнения и системы с переменными коэффициентами. Многообразие решений. Формула Лиувилля-Остроградского ([1], § 14,17,18, 21).
  4. Теоремы о выпрямлении векторного поля, о непрерывной зависимости решения от начальных условий и от параметров ([1], § 2,3; [10], § 7, 22).
  5. Гладкость решения по начальным данным и параметрам ([1], § 24).
  6. Автономные системы, Классификация особых точек. Теоремы об индексе. Теорема Пуанкаре-Бендиксона ([1], § 15,16; гл.VII § 1-4).
  7. Устойчивость по Ляпунову. Теорема Ляпунова об устойчивости по первому приближению ([1], § 26).
  8. Предельные циклы ([1], § 28).
  9. Дифференциальные уравнения в частных производных первого порядка ([2], часть 2, гл. 1, § 1).
  10. Элементы вариационного исчисления. Функция Лагранжа (лагранжиан). Условия экстремума. Уравнения Эйлера-Лагранжа. Импульс. Гамильтониан. Уравнения Гамильтона-Якоби ([2], часть 1, гл. 2; [3], гл.1; [9], часть 1, гл.5, § 31-36, гл.6, § 37-38).
  11. Задачи оптимального управления. Принцип максимума Понтрягина ([3], гл.I).
  12. Теоремы Фредгольма для интегральных уравнений второго рода ([4], часть 4, § 17-18; [7], гл.II § 4).
  13. Интегральные уравнения с эрмитовым ядром; теорема Гильберта-Шмидта ([4], гл. 4, § 19-22; [7], гл.II § 5).
  14. Понятие о характеристиках уравнений в частных производных. Задача Коши; теорема Ковалевской. Классификация уравнений в частных производных ([4], гл.1, § 3; [6], гл.1, § 2,3; [7], гл.1, § 1,2).
  15. Физические задачи, приводящие к эллиптическим уравнениям. Свойства гармонических функций (гладкость, теоремы о среднем, принцип максимума, теорема об устранении особенности, теорема Лиувилля). Фундаментальное решение уравнения Лапласа ([4], гл.1, § 2; гл.5, § 24,27; [5], гл.4, § 1,2; [6], гл.3, § 27-30; [7], гл.1, § 3).
  16. Решение краевых задач для уравнения Лапласа методом потенциалов ([4], гл.5, § 27,28,31; [5], гл.4, § 5; дополнение 1, § 3; [6], гл.3, § 31-36).
  17. Обобщенные решения основных краевых задач для эллиптического уравнения второго порядка. Разрешимость краевых задач и гладкость обобщенных решений ([7], гл.6, § 1,2; [8], гл.2).
  18. Вариационный метод решения краевых задач для эллиптического уравнения второго порядка. Метод Ритца ([7], гл.4, § 1).
  19. Задача на собственные значения. Разложение в ряды по собственным функциям ([4], гл.5, § 21,22; [7], гл.4, § 1, п.3-5; [8], гл.2, § 4).
  20. Свойства решений однородного уравнения теплопроводности (гладкость, принцип максимума). Фундаментальное решение. Задача Коши ([4], гл.1, § 2; гл.3, § 11,16; [5], гл.3, § 1; гл.4, § 1; [6], гл.3, § 38-40; [7], гл.6, § 1; [8], гл. 3).
  21. Основные смешанные задачи для уравнения теплопроводности; классические и обобщенные решения смешанных задач ([4], гл.6, § 34; [5], дополнение 1, § 2; [7], гл.5, § 1; [8], гл.3).
  22. Конечная гладкость решения уравнения. Фундаментальное решение. Задача Коши ([4], гл.1, § 2; гл.3, § 12-14; [5], гл.2, § 2, гл.5, § 1,2; [6], гл.2, § 11-13; [7], гл.5, § 1; [8], гл.4).
  23. Основные смешанные задачи для волнового уравнения. Метод Фурье решения смешанных задач. Метод Галеркина решения смешанных задач для волнового уравнения ([4], гл.6, § 33; гл.2, § 3; гл.5, § 3; [6], гл.2, § 17-23; [7], гл.5, § 2; [8], гл.4).
  24. Обобщенные функции. Свертка обобщенных функций. Обобщенные функции медленного роста; преобразование Фурье обобщенных функций медленного роста ([4], гл.2, § 5-9; гл.3, § 11).
  25. Пространства дифференцируемых функций, эквивалентные нормировки пространств H21 и W1. Вложение пространства Wk в Wl ([2], часть 1, гл.3, § 3-6; [8], § 1-7).
  26. Дробные пространства Соболева. Теоремы о следах (прямые и обратные) ([9], часть 3, гл.1,2).


ЛИТЕРАТУРА

  1. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974.
  2. Смирнов В.И. Курс высшей математики. Т.4, ч.1,2. М.: Наука, 1981.
  3. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М.: Наука, 1979.
  4. Владимиров В.С. Уравнения математической физики. М.: Наука, 1084.
  5. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1981.
  6. Петровский И.Г. Лекции об уравнениях с частными производными. М.: Физматгиз, 1961.
  7. Михайлов В.П. Дифференциальные уравнения в частных производных. М.: Наука, 1983.
  8. Ладыженская О.А. Краевые задачи математической физики. М.:Наука, 1973.
  9. Избранные главы анализа и высшей алгебры. Л.: ЛГУ. 1981.
  10. Арнольд В.М. Обыкновенные дифференциальные уравнения. М.: Наука,1971.
  11. Хартман Ф. Обыкновенные дифференциальные уравнения. М.:Мир,1970.


Дополнительные вопросы к кандидатскому минимуму

по специальности 01.01.02 – дифференциальные уравнения и математическая физика

  1. Вырождающиеся эллиптические уравнения. Задача Дирихле для вырождающихся эллиптических уравнений ([1]).
  2. Уравнения смешанного типа. Задача Дирихле для уравнения смешанного типа. Спектральные вопросы дифференциальных уравнений смешанного типа в неограниченной области ([2], [3]).
  3. Достаточное условие разделимости нелинейного уравнения Штурма-Лиувилля ([4]).
  4. Метод компактности для нелинейных дифференциальных уравнений ([5], [6]).
  5. Существование обобщенного решения симметричной гиперболической системы дифференциальных уравнений в частных производных ([7]).
  6. Метод Титчмарша доказательства существования решения сингулярного уравнения Штурма – Лиувилля ([8], §1,2).
  7. Обобщенные решения краевых задач для эллиптических уравнений, существование, единственность и гладкость обобщенных решений ([9], гл.4).
  8. Существование и единственность обобщенного решения смешанной задачи для гиперболического уравнения ([9], гл.5).
  9. Существование и гладкость обобщенного решения для параболического уравнения ([9], гл.6 ).
  10. Метод Галеркина доказательства существования обобщенного решения смешанной задачи для гиперболического уравнения ([9]).
  11. Краевая задача для обыкновенного дифференциального уравнения второго порядка ([10], гл.7).
  12. Обобщенная формула Бореля-Помпею ([11], [12]).
  13. Интегральная формула Коши ([11]).
  14. Условие Коши-Римана для аналитических функций ([11]).
  15. Задача Римана-Гильберта для обобщенных аналитических функций ([12], [13]
  16. Задача сопряжения для аналитических функций ([13]).


Литература

  1. Смирнов М.М. Вырождающиеся эллиптические и гиперболические уравнения. М., 1966.
  2. Бицадзе А.В. Уравнения смешанного типа. М.,1959.
  3. Кальменов Т.Ш, Муратбеков М.Б. Спектральные свойства оператора смешанного типа. Шымкент:Гылым, 1997.
  4. Мынбаев К.Т. Отелбаев М.О Весовые функциональные пространства и cпектр дифференциальных операторов. М:Наука, 1988.
  5. Лионс Ж.Л. Некоторые методы решения нелинейных краевых задач. М.:Мир, 1972.
  6. Куфнер А., Фучик С. Нелинейные дифференциальные уравнения. М.:Наука, 1988.
  7. Нагумо М. Лекций по современной теории уравнений в частных производных. М.: Мир, 1967.
  8. Отелбаев М.О. Оценки спектра оператора Штурма–Лиувилля. Алматы:Гылым, 1990.
  9. Михайлов В.П. Дифференциальные уравнения в частных производных. М.:Наука, 1983.
  10. Лизоркин П.И. Курс дифференциальных и интегральных уравнений с дополнительными главами анализа. М.:Наука, 1981.
  11. Бицадзе А.В. Методы теории функций комплексного переменного. М., 1974.
  12. Векуа И.Н. Обобщенные аналитические функций. М., 1959.
  13. Гахов Ф.Д. Краевые задачи. М., 1961.




i-bin/footer.php"; ?>