Определители 2-го и 3-го порядков: определения и применение к решению систем линейных уравнений методом Крамера
| Вид материала | Документы |
- Лекции по предмету "аналитическая геометрия и линейная алгебра", 82.08kb.
- Контрольная работа по курсу «Линейной алгебры и математического программирования», 99.84kb.
- Решение систем линейных уравнений методом крамера, 19.06kb.
- Неравенств и, если «да», то найдите общее решение и частное решение двумя способами:, 11.47kb.
- Вопросы к экзамену по курсу «Высшая математика часть, 14.58kb.
- Тематическийпла н, 46.68kb.
- Элемен ты линейной и векторной алгебры, 26.56kb.
- Тематика курсовых работ по линейной алгебре Матрицы и определители: реализация основных, 8.06kb.
- Вопросы к экзамену 1 семестр, 56.89kb.
- «Численные методы», 64.5kb.
- Определители 2-го и 3-го порядков: определения и применение к решению систем линейных уравнений методом Крамера.
- Свойства определителей 2-го и 3-го порядков. Разложение определителя 3-го порядка по элементам строк и столбцов. Способы вычисления определителей 3-го порядка.
- Определитель n-го порядка: определение, свойства, вычисление и применения.
- Обратная матрица: определение, вычисление и применение.
- Матрицы и линейные операции над ними.
- Умножение матриц и его применение.
- Ранг матрицы: определения, вычисление и применение.
- Система линейных уравнений: основные определения и задачи.
- Теорема Кронекера – Капели и её применение.
- Метод Крамера.
- Система линейных однородных уравнений: свойства её решений и фундаментальная система решений.
- Метод Гаусса и его матричная схема.
- Векторы: основные определения, ориентация, умножение на числа и сложение.
- Векторный базис на прямой, на плоскости и в пространстве. Координаты вектора.
- Основная теорема векторной алгебры (с доказательством).
- Ортогональная проекция вектора на ось и её применение. Основные задачи векторной алгебры и их решения методами систем линейных уравнений.
- Скалярное произведение векторов: определение, свойства и применение. Направляющие косинусы вектора.
- Векторное произведение векторов: определение, свойства и применение.
- Смешанное произведение векторов: определение, свойства и применение. Двойное векторное произведение: определение и способы вычисления.
- Система координат на прямой, на плоскости и в пространстве. Координаты точки.
- Деление отрезка в данном отношении. Вычисление площадей и расстояния между двумя точками.
- Общее уравнение плоскости: определение и исследование. Задача о нормальном векторе плоскости.
- Общее уравнение прямой на плоскости: определение и исследование.
- Связь между различными заданиями прямой на плоскости.
- Взаимное расположение двух прямых на плоскости.
- Взаимное расположение двух прямых в пространстве.
- Взаимное расположение прямой и плоскости в пространстве.
- Параметрическое задание прямой на плоскости в пространстве.
- Взаимное расположение двух и трех плоскостей в пространстве.
- Параметрическое задание плоскости в пространстве.
- Определение расстояний: 1) от точки до прямой на плоскости и в пространстве; 2) от точки до плоскости; 3) между двумя скрещивающимися прямыми.
- Кривые второго порядка на плоскости: свойства, построение.
- Поверхности второго порядка в пространстве: свойства, построение.
- Функция одного вещественного аргумента: определения, области определения и значений, график и способы задания.
- Пределы функции: определения (на языке “ε-δ”и теоретическое), свойства, левый и правые пределы.
- Основная теорема пределов (с доказательством).
- Точки разрыва функции и их классификация.
- Непрерывность функции: определение, свойства. Свойства функций, непрерывных на замкнутом ограниченном отрезке.
- Непрерывность функции на языке приращений ( с доказательством).
- Бесконечно большие и бесконечно малые величины и связь между ними, их применение.
- Эквивалентные бесконечно малые величины и их применение.
- Сравнение бесконечно малых величин.
- Замечательные пределы и их доказательство методом Лопиталя.
- Производная функции: определение, свойства, геометрический смысл.
- Связь производной с непрерывностью (с доказательством).
- Производные от обратной и параметрических функций.
- Производные от сложной и неявной функций.
- Таблица производных от тригонометрических функций (с доказательством).
- Производная от показательно-степенной функции (с доказательством).
- Таблица производных от логарифмической функции и от функций, производные которых получены с применением логарифмической функции.
- Дифференциал функции: определение, свойства, геометрический смысл и применение.
- Производные и дифференциалы высших порядков. Формулы Тейлора и Маклорена и их применение.
- Теорема Коши: формулировка и доказательство и применение.
- Теорема Лагранжа: формулировка, доказательство, геометрический смысл и применение.
- Теорема Ролля: формулировка, доказательство, геометрический смысл и применение.
- Теорема Лопиталя: формулировка, доказательство и применение к вычислению пределов.
- Возрастание и убывание функции.
- Экстремум функции: определения, необходимые условия существования по первой производной (с доказательством).
- Экстремум функции: определения, достаточные условия существования по первой производной (с доказательством).
- Экстремум функции: определения, достаточные условия существования по второй производной (с доказательством).
- Наибольшее и наименьшее значения функции на замкнутом ограниченном интервале.
- Выпуклость и вогнутость графика функции: определения и условия существования.
- Точки перегиба графика функции: определение и условия существования.
- Поведение функции в бесконечности. Асимптоты графика функции.
- Исследование функций и построение их графиков.
ВАРИАНТ 27
Найти уравнения касательной и нормали к кривой y = 3t2 + 7, x = t –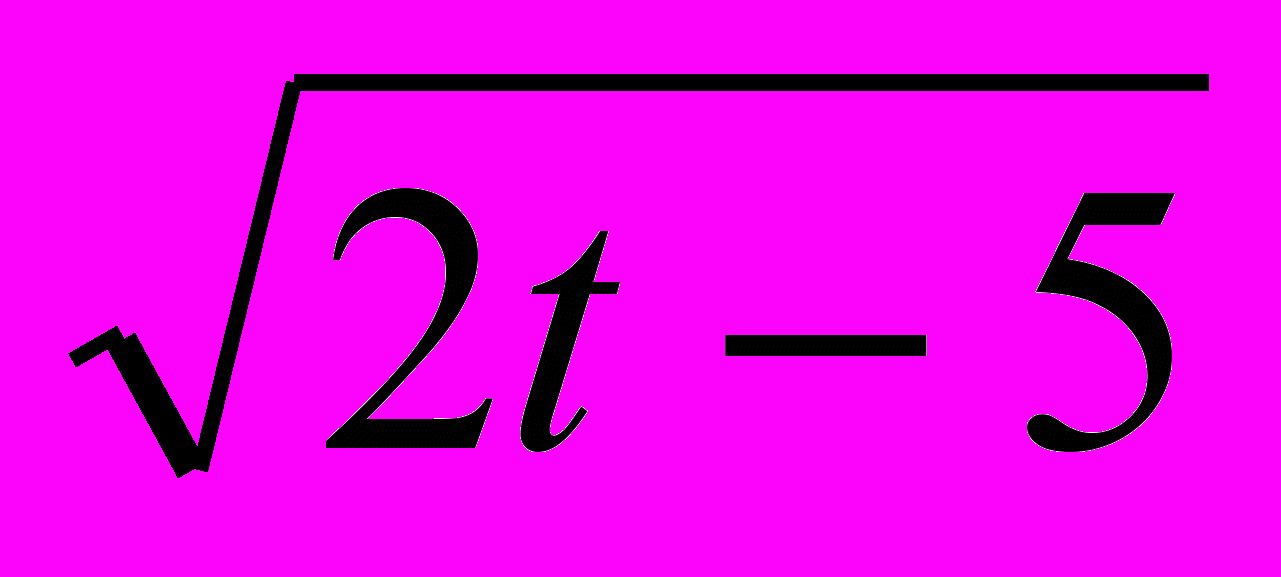
в точке t = 6.
- Используя правило Лопиталя, вычислить пределы.
; 
; 
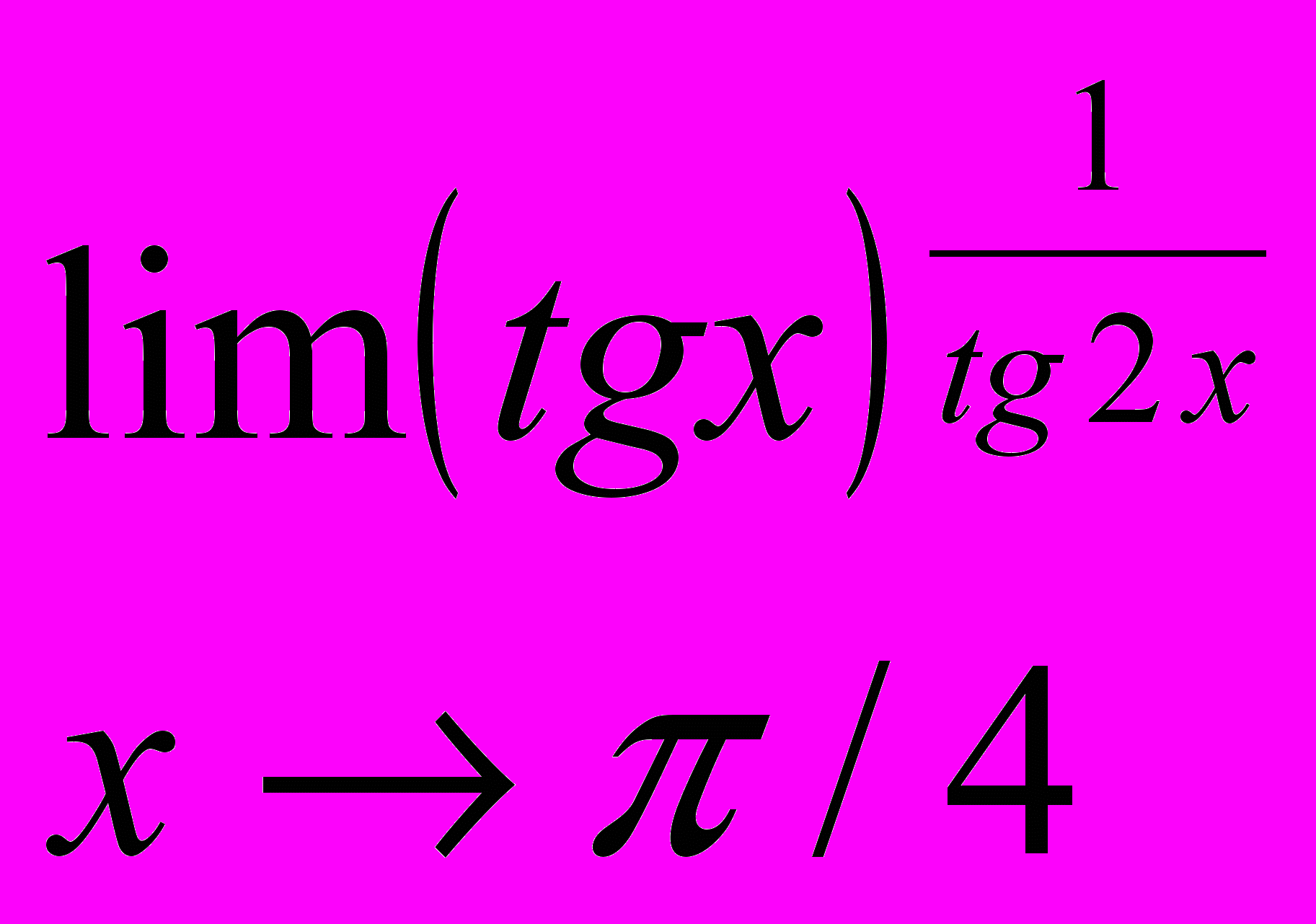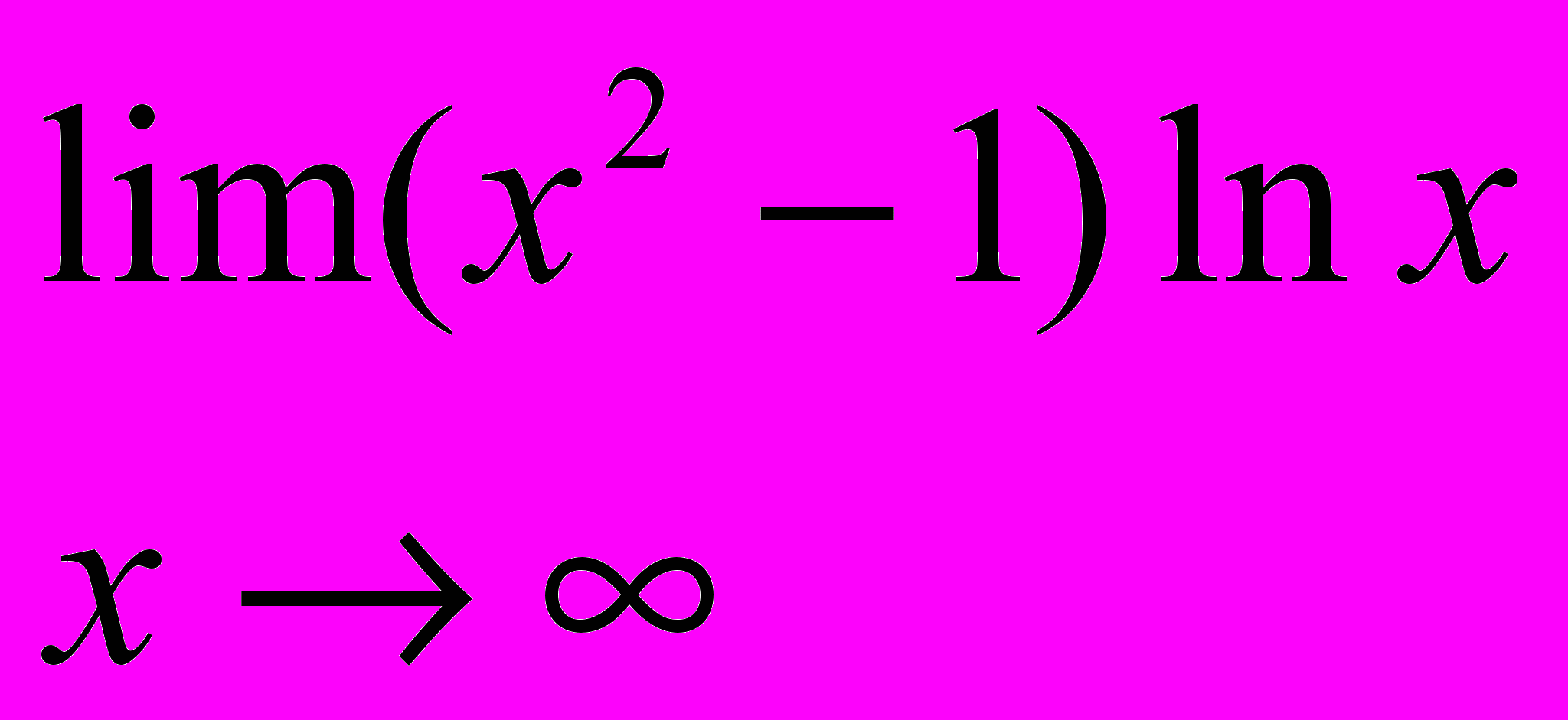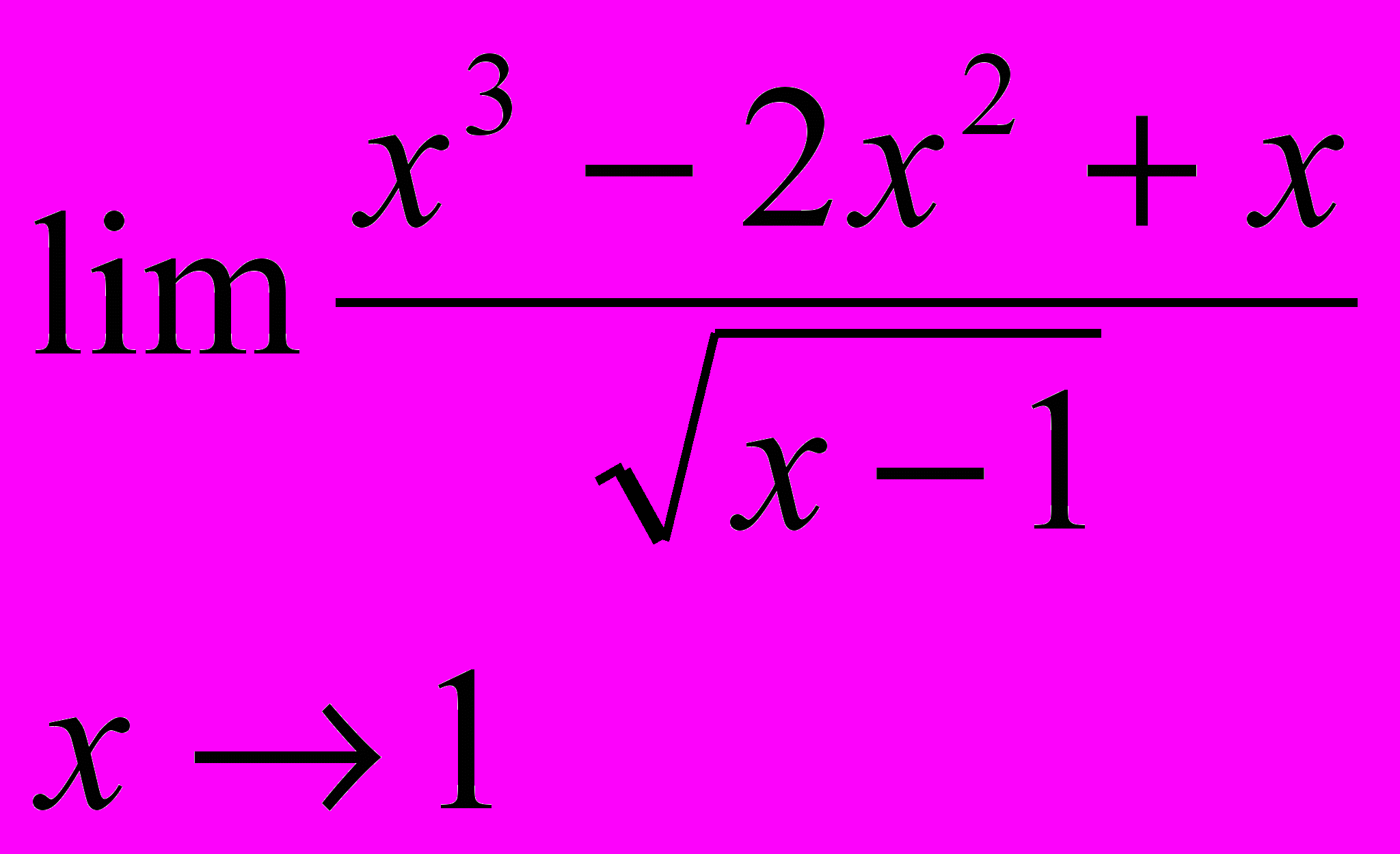
Найдите наибольшее, наименьшее значения и экстремумы функции у(х) на отрезке [0; 4], y(x) = x +2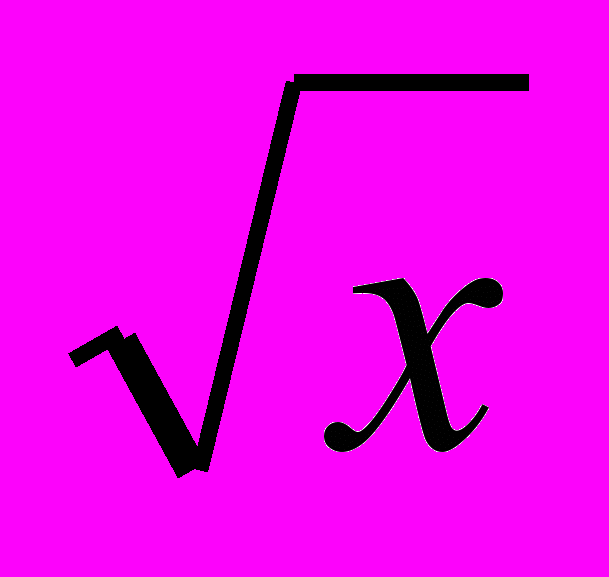
.
4. f(x) = 3x6 + x2 + 2. Посчитайте приближенно f(1,03).
5. Провести полное исследование функции и построить её график.
