Элемен ты линейной и векторной алгебры

Вид материала

Документы

Содержание Разложение определителя по элементам строки или столбца

Подобный материал:

• Рабочая программа курса «высшая математика (элементы аналитической геометрии и линейной, 67.54kb.
• Тема: «теория матриц» Основная задача линейной алгебры, 28.88kb.
• Некоммутативная геометрия, 36.84kb.
• Рабочая программа дисциплины электричество, магнетизм, колебания и волны (эмв) направление, 394.49kb.
• Задачи дискретного программирования Постановка проблемы, 14.8kb.
• Задачи математического программирования Методы принятия решений, 37.8kb.
• «Решение задач линейной алгебры. Операции с матрицами», 20.33kb.
• Содержание глав (модулей) и тем по курсу высшей математики, 46.76kb.
• Контрольная работа по курсу «Линейной алгебры и математического программирования», 99.84kb.
• " Геометрия и топология "(010500) Общая трудоемкость, 12.81kb.

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ

1. Определители и их свойства. Вычисление определителей.
   
2. Матрицы и операции над ними.
   
3. Системы линейных уравнений. Метод Гаусса, правило Крамера, матричный метод решения систем.
   
4. Векторы, операции над векторами.
   
5. Скалярное, векторное и смешанное произведение векторов, их свойства и приложения.
   

Определители и их свойства

Определение: Определителем n – го порядка называется квадратная таблица чисел, состоящая из n строк и n столбцов.

det A=

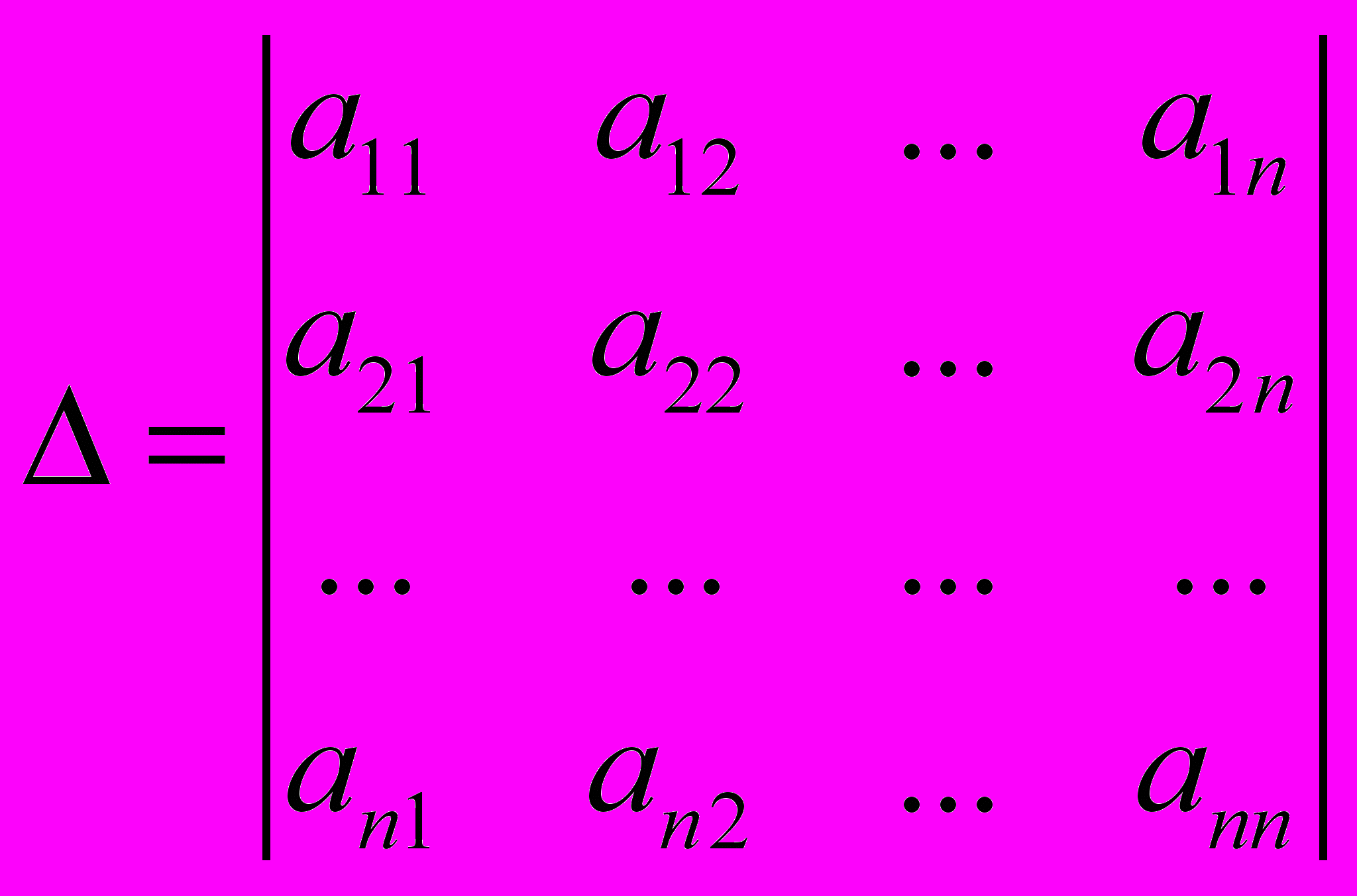
- элементы определителя, где i – номер строки, а j – номер столбца,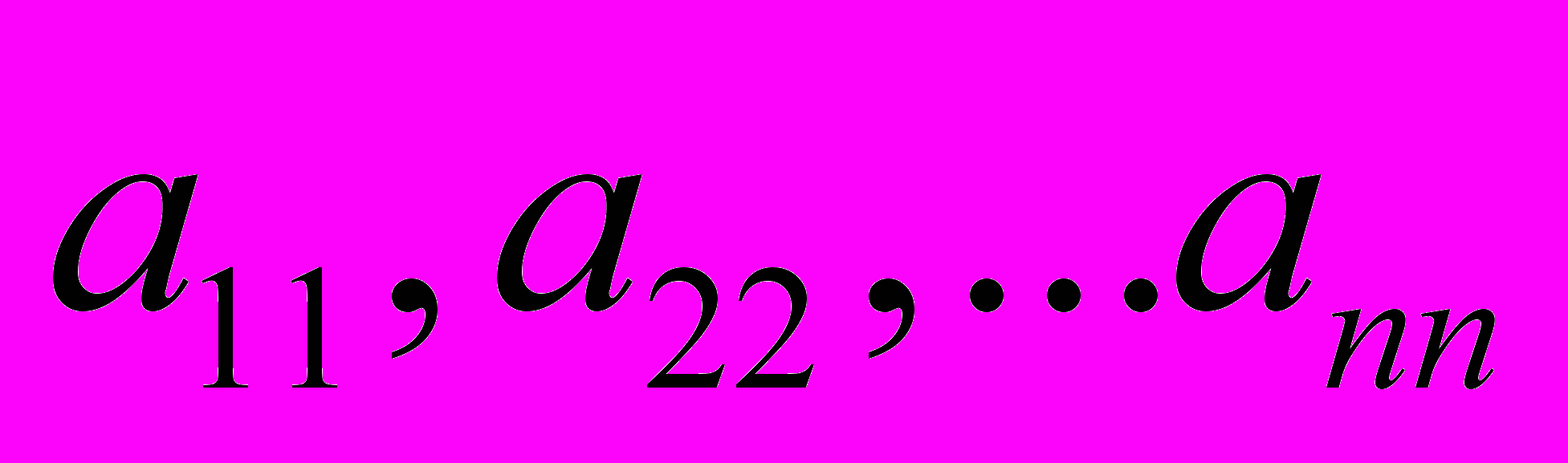

- элементы главной диагонали

Побочная диагональ идет из левого нижнего угла в правый верхний.

Определение: Определителем второго порядка называется число, определяемое для чисел 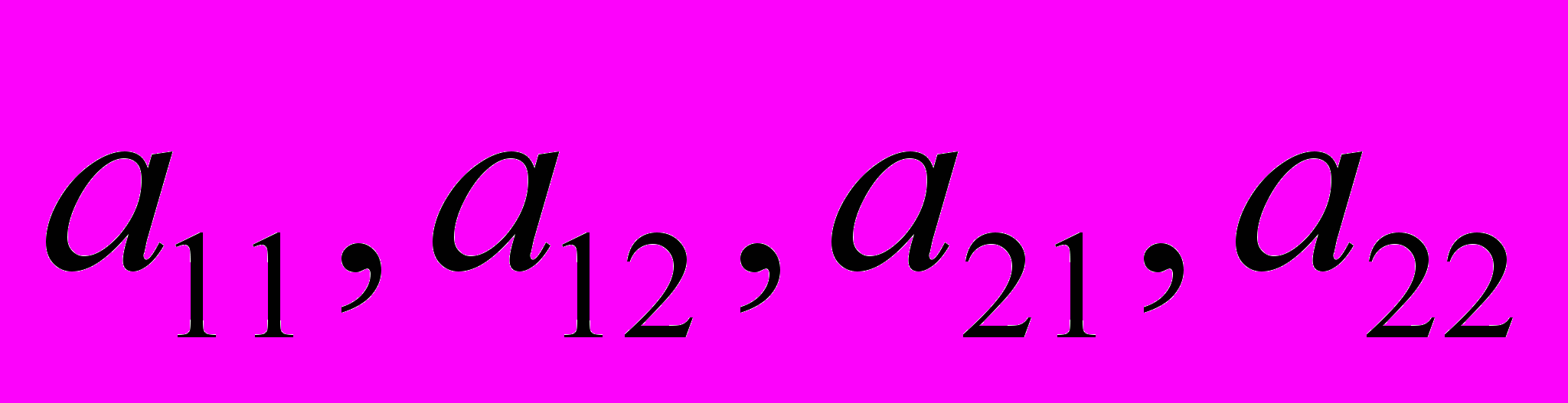по следующему правилу: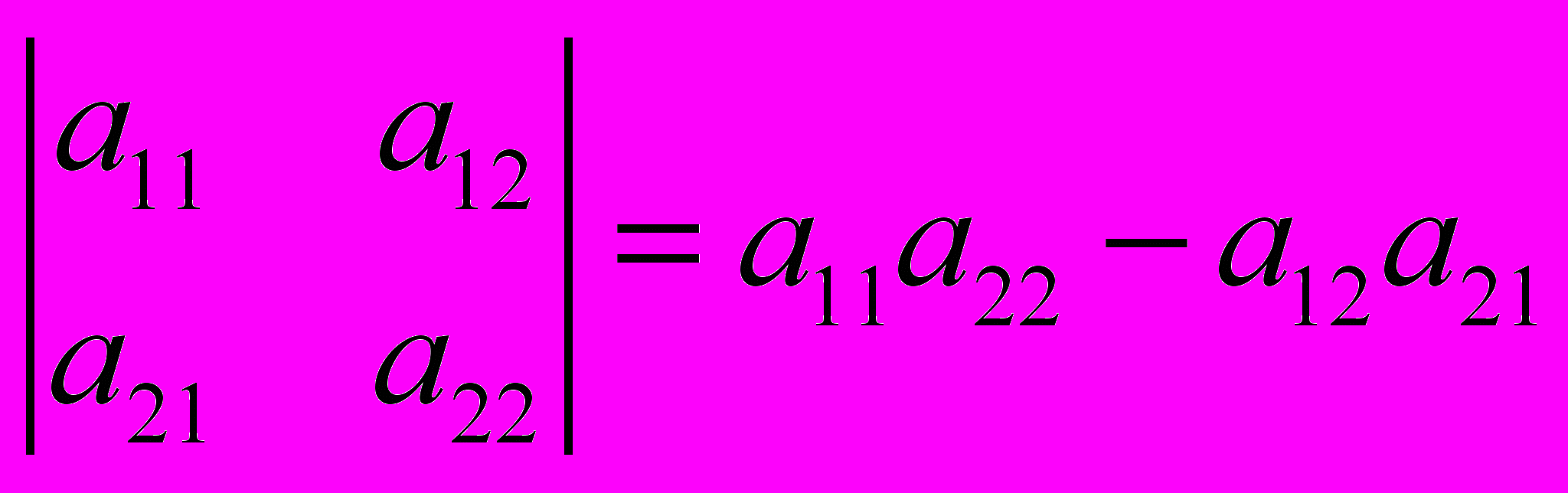



Пример:.



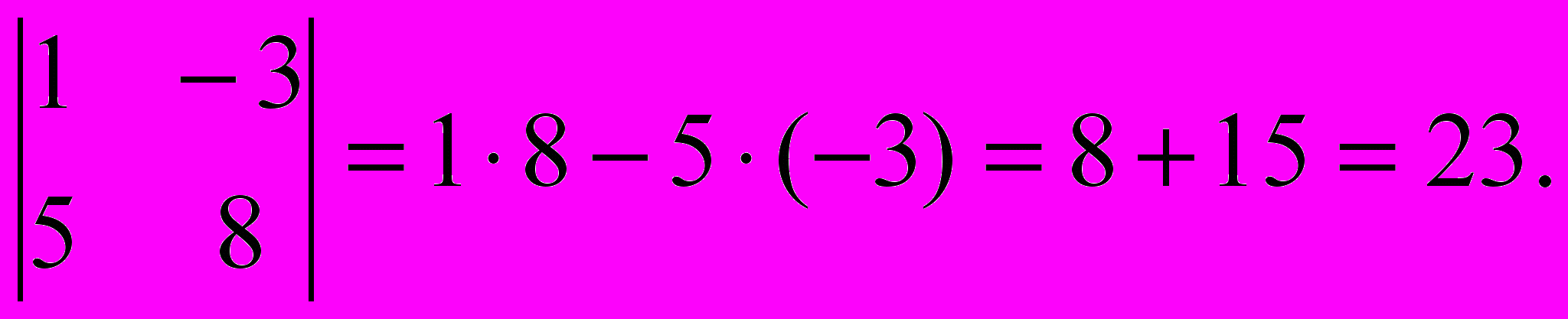
Определение: Определителем третьего порядка называется число, определяемое девятью числами по правилу треугольника (звезда):



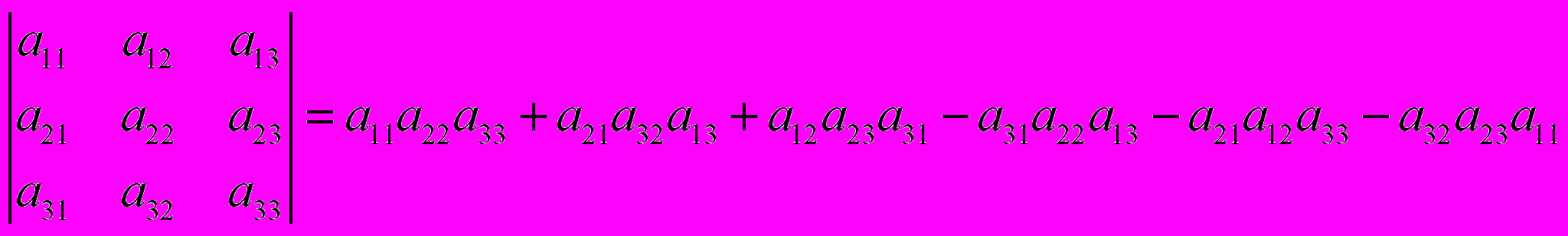
Только для определителей третьего порядка существуют более наглядные правила вычисления определителя. Полезно пользоваться правилом треугольника.



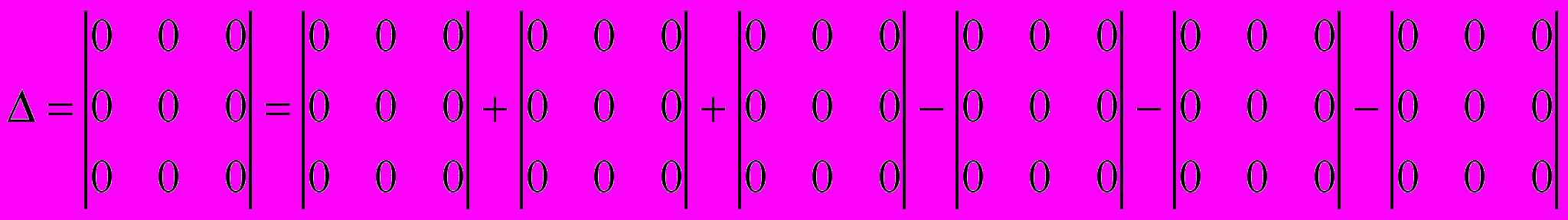
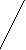
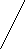
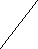
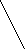
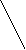
Пример:



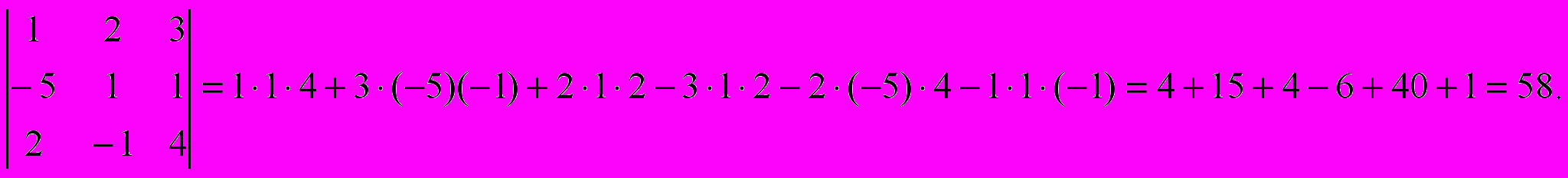
Свойства определителей:

Свойство 1. Определитель не изменяется при транспонировании, т.е.



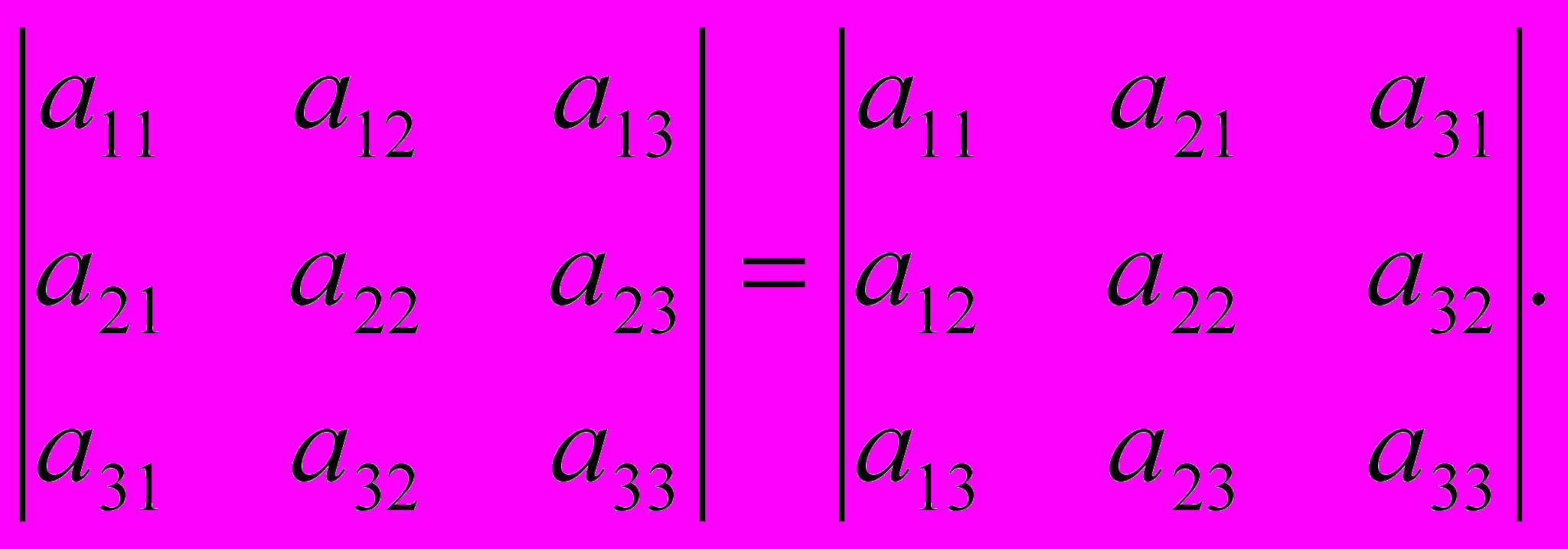
Свойство 2. Если все элементы столбца (строки) равны нулю, то определитель равен нулю.

Свойство 3. Постоянный множитель всех элементов некоторой строки (или столбца) выносится за знак определителя.

Свойство 4. Если поменять местами какие-либо две строки (или столбца), то определитель изменит знак, не изменившись по абсолютной величине.

Свойство 5. Определитель, имеющий две равные строки (или столбца), равен 0.

Свойство 6. Если соответствующие элементы двух столбцов (строк) определителя пропорциональны, то величина определителя равна нулю.

Свойство 7. Определитель не изменится, если к элементам некоторого столбца (строки) прибавить (вычесть) элементы другого столбца (строки), умноженные на одно и то же число, не равное нулю.


Разложение определителя по элементам строки или столбца

Определение: Минором M_ij элемента a_ij определителя называется определитель, полученный вычеркиванием i - той строки и j – го столбца, на пересечении которых расположен этот элемент.

Определение: Алгебраическим дополнением A_ij элемента a_ij называется минор этого элемента M_ij умноженный на (-1)^i+j, т.е.

A_ij = (-1)^i+j M_ij,

Пример: .

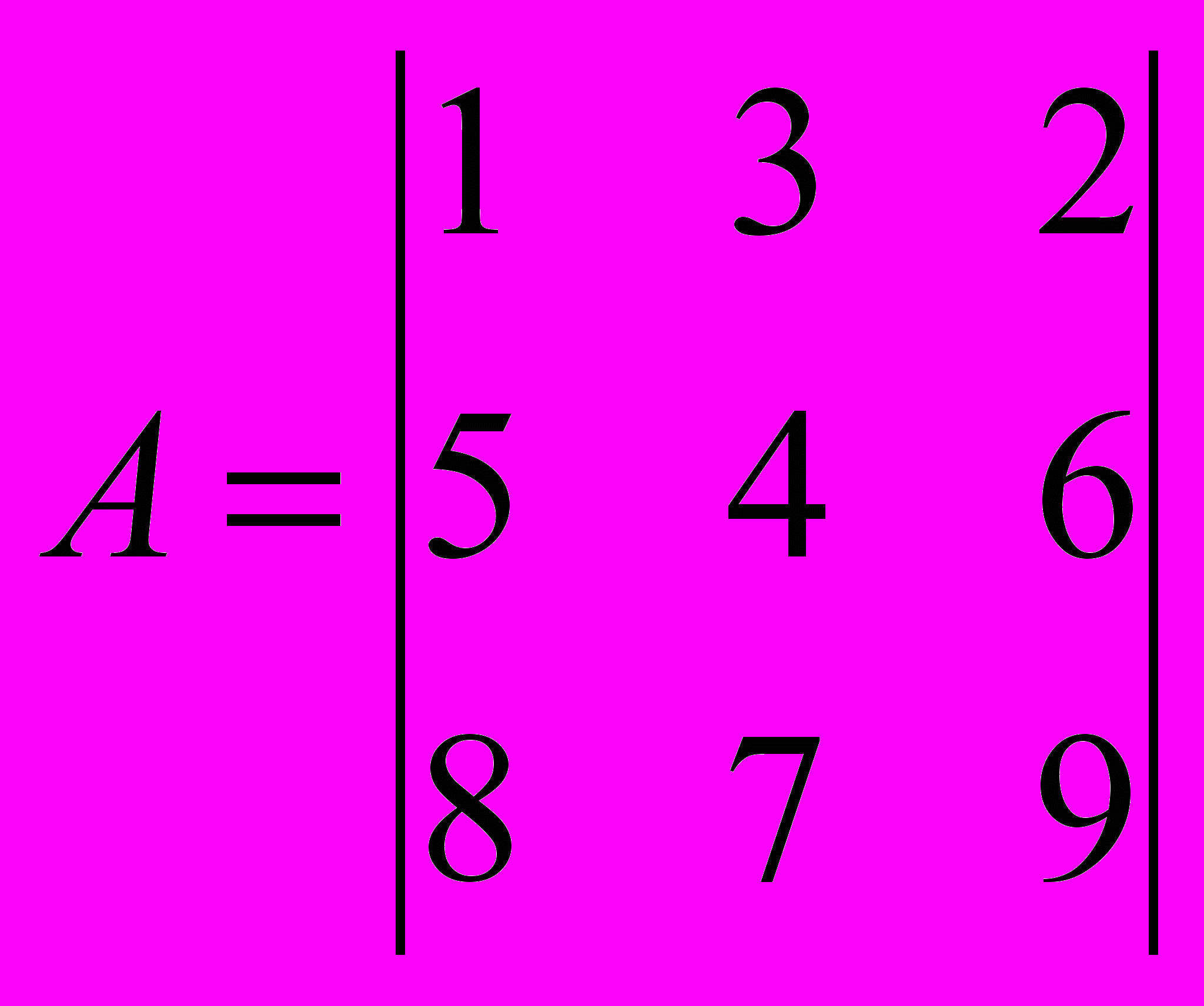Минор М₁₂ = . (вычеркнули первую строку и второй столбец) = -3.

Минор М₂₃ = 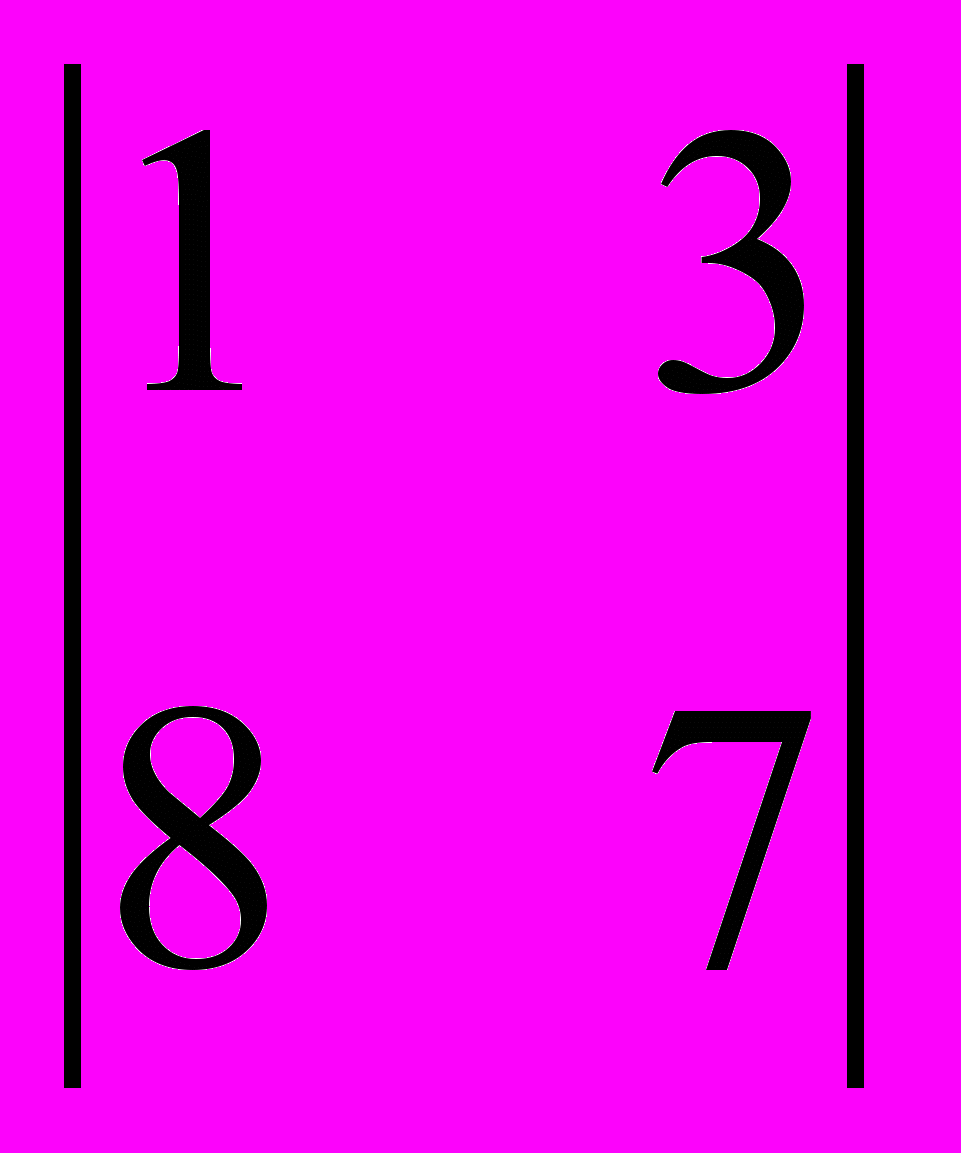. (вычеркнули вторую строку и третий столбец) = -17.

Определитель равен сумме произведений элементов какого-нибудь столбца (строки) на их алгебраические дополнения.

Запишем разложение определителя по первой строке:



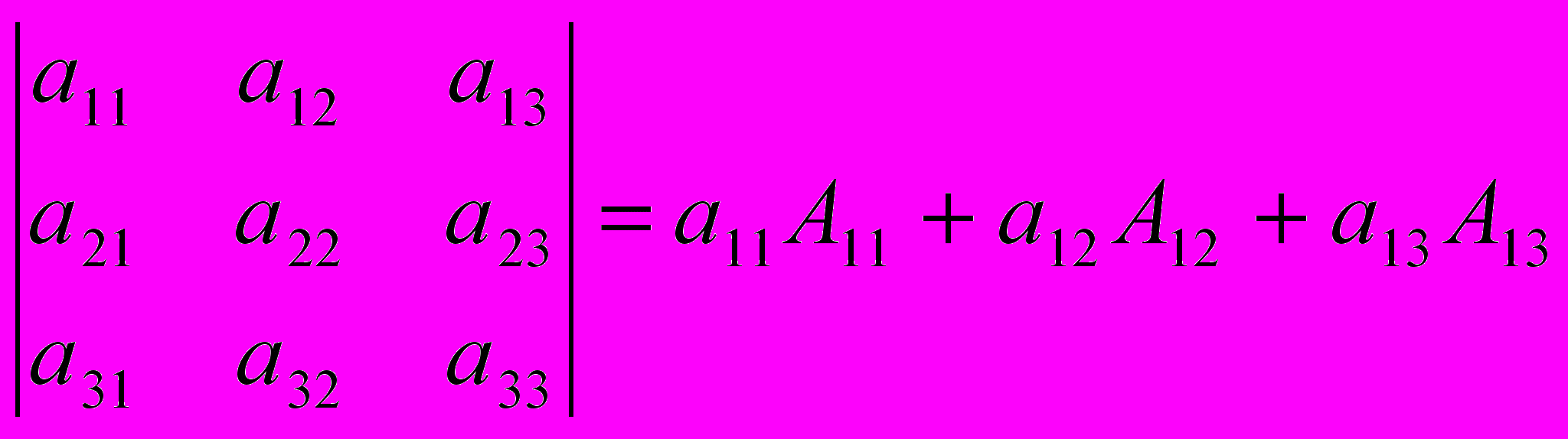
Пример: Вычислить определитель А = 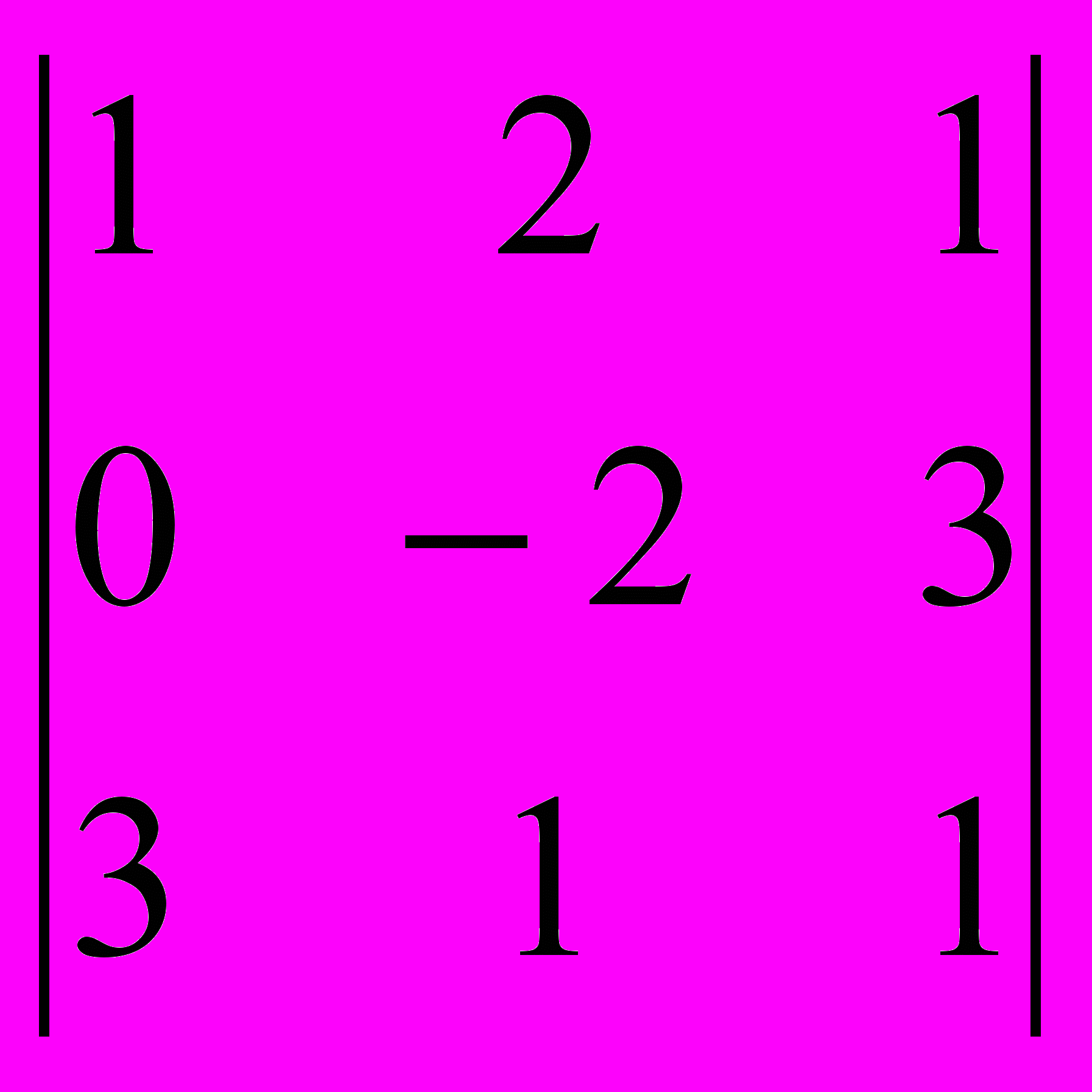, разлагая его по первой строке.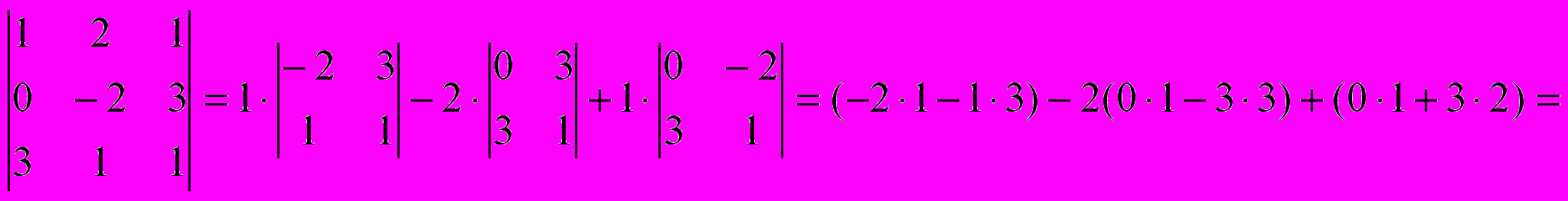




= -5 + 18 + 6 = 19.