Некоммутативная геометрия

Вид материала

Документы

Содержание 2. Элементы теории операторных алгебр и модулей. 3. Операторная теория. 4. Циклические (ко)гомологии. 5. Эллиптические операторы и теоремы об индексе. 6. Приложения некоммутативной геометрии к задачам топологии и геометрии.

Подобный материал:

• Урок по теме «Первый признак равенства треугольников», 38.38kb.
• Программа разработана на основе авторской программы Белошистой А. В. Пояснительная, 96.55kb.
• Шихаб геометрия тензора конгармонической кривизны приближенно келеровых многообразий, 138.61kb.
• Рабочей программы учебной дисциплины геометрия уровень основной образовательной программы, 74.17kb.
• Рабочая учебная программа дисциплины (модуля) Алгебра и геометрия, 207.66kb.
• Геометрия на сфере, 236.78kb.
• Методика проектирования инструмента. Содержание рабочего чертежа на него. Формы, геометрия, 172.74kb.
• Учебно-методический комплекс по дисциплине опд. Ф. 01. 01 «Начертательная геометрия., 480.75kb.
• Экспериментальная программа дисциплины «Начертательная геометрия», 93.2kb.
• Программа «Живая геометрия», 88.49kb.

НЕКОММУТАТИВНАЯ ГЕОМЕТРИЯ

доц. В.М. Мануйлов, проф. А.С. Мищенко, проф. Е.В. Троицкий

1. Элементы теории векторных расслоений и топологической 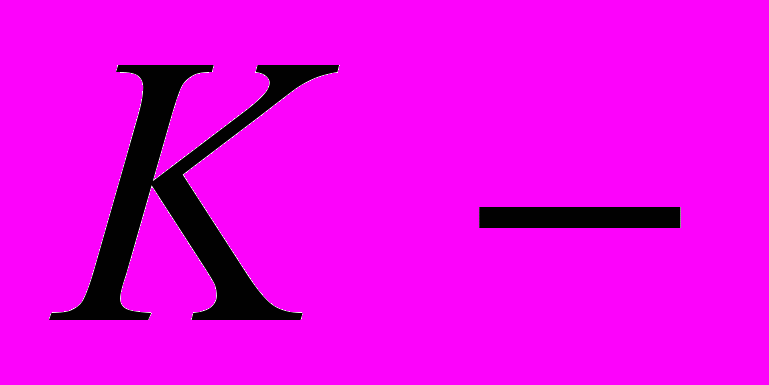теории.

1. Векторные расслоения.

2. Гомотопическая теория векторных расслоений.

3. 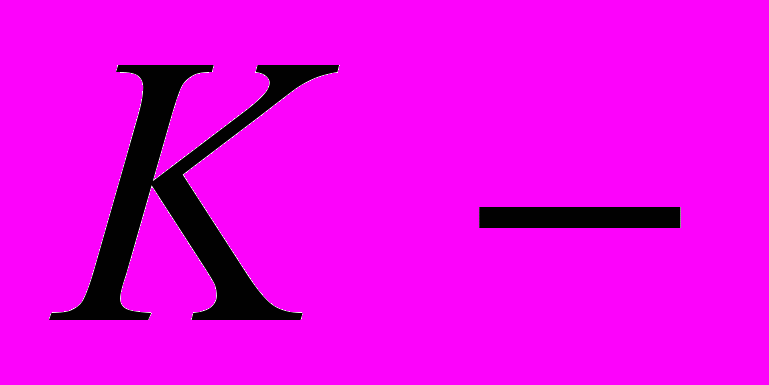группы.

4. Периодичность Ботта в 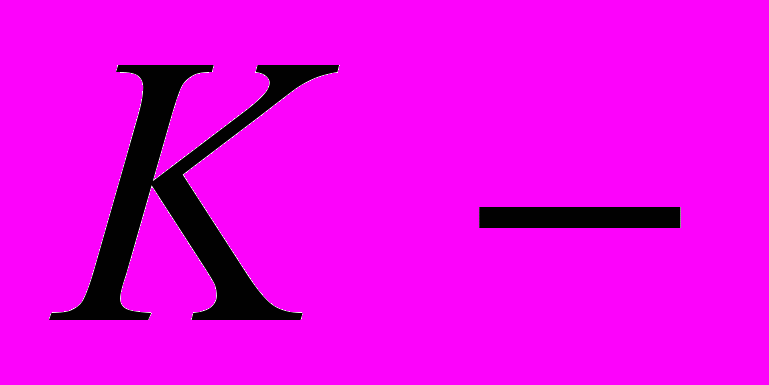теории.

5. Изоморфизм Тома.

6. Характеристические классы и характер Чженя.

7. Вычислительные методы 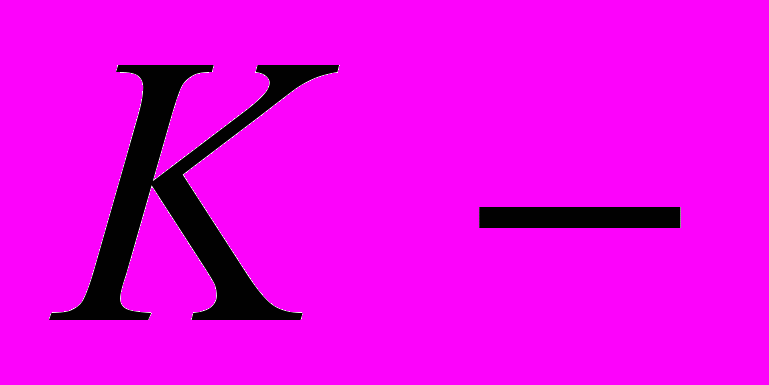теории.

^ 2. Элементы теории операторных алгебр и модулей.

1.  Элементы теории 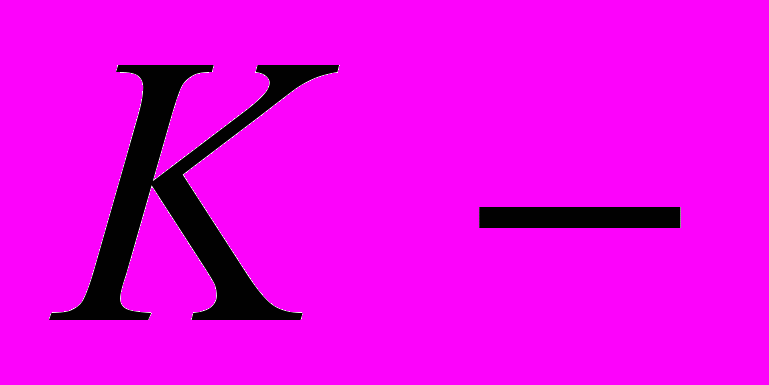алгебр.

2. 1-я и 2-я теоремы Гельфанда-Наймарка. Формулировка спектраль­ной теоремы.

3. Основные классы и примеры 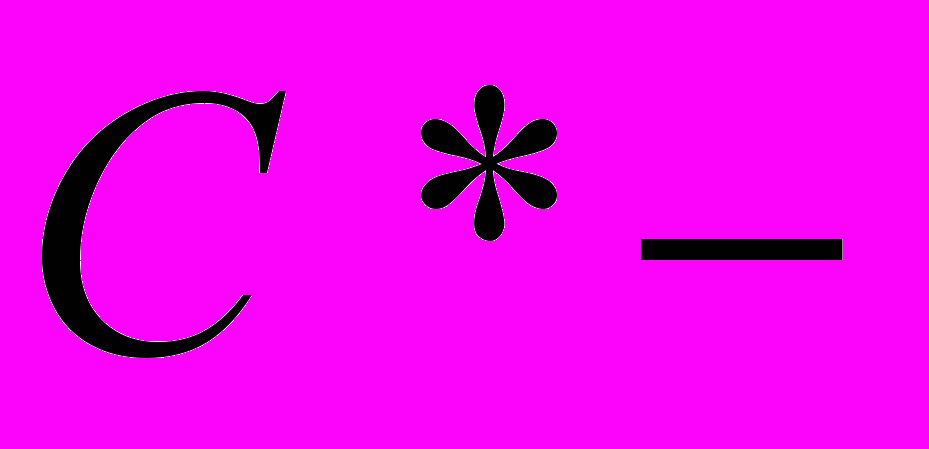алгебр (групповые 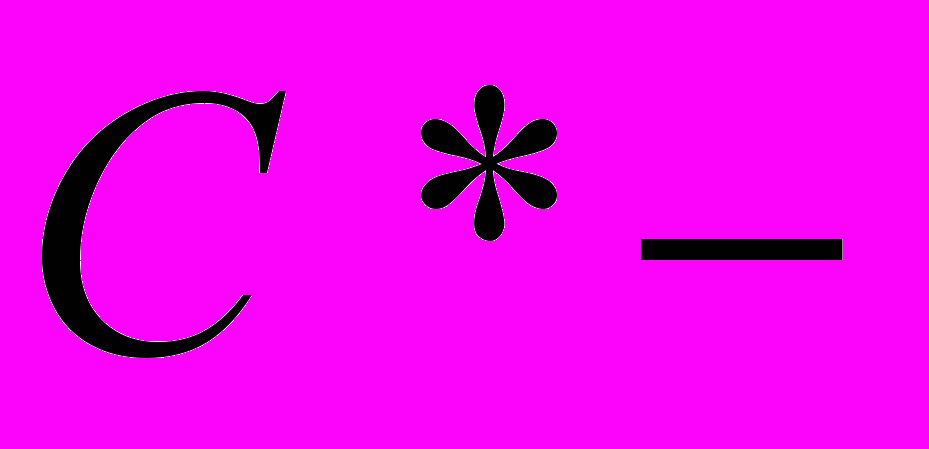алгебры локально компактных групп, 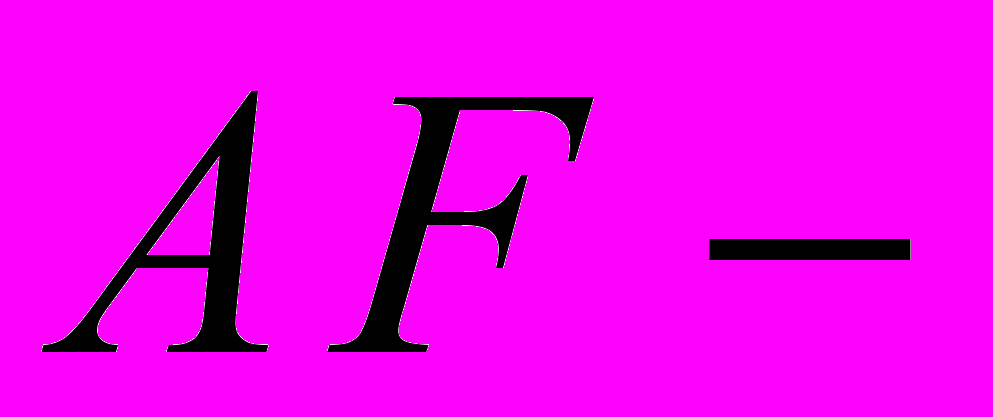алгебры, алгебра Калкина, алгебры иррационального вращения, алгебры Кунца, алгебры фон Неймана, факторы, (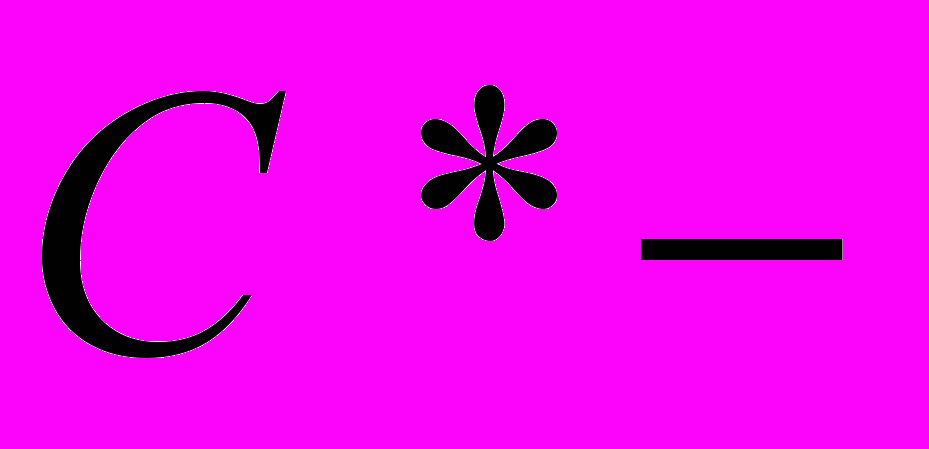алгебры слоения, 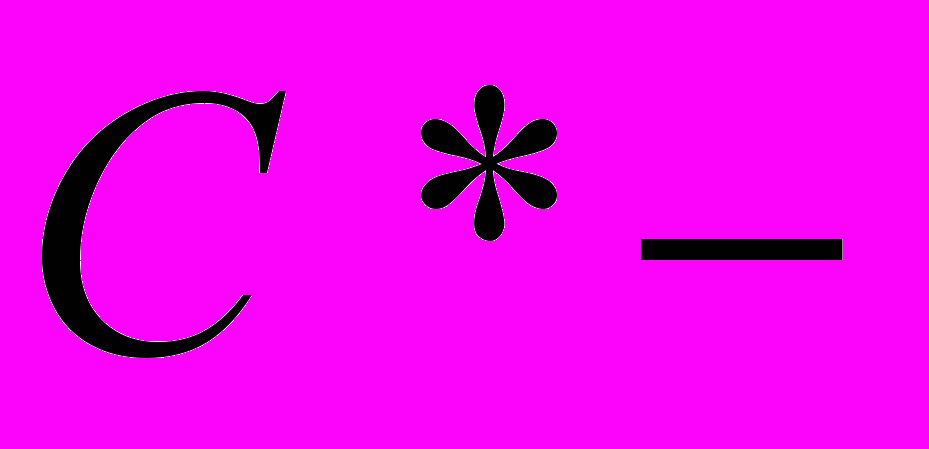алгебра группоидов, простран­ства с особенностями и их 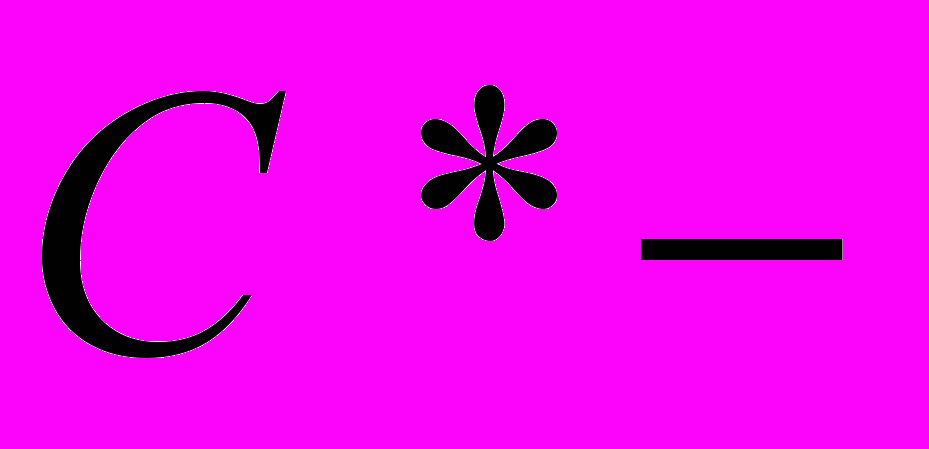алгебры).

4. Гильбертовы модули и операторы в них.

5. Теорема Каспарова о стабилизации.

6. Алгебры операторов в гильбертовых модулях. Мультипликаторы.

7. Теория гомотопий в категории 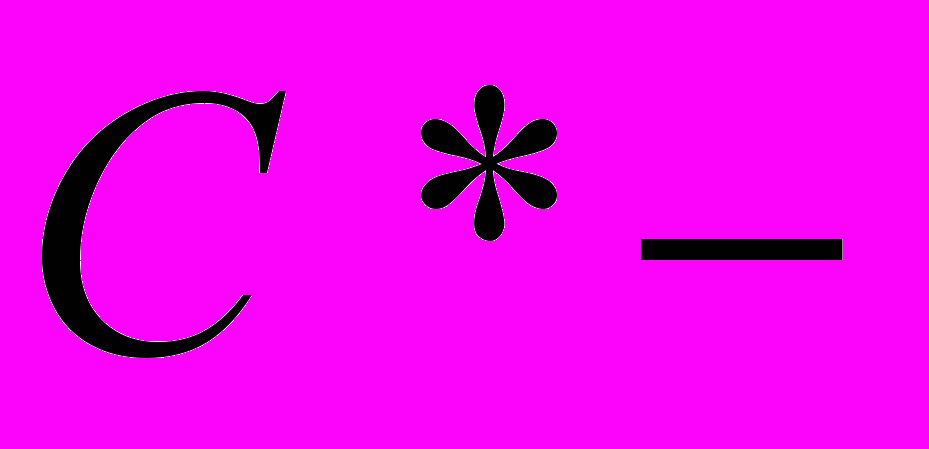алгебр.

8. Вычисление 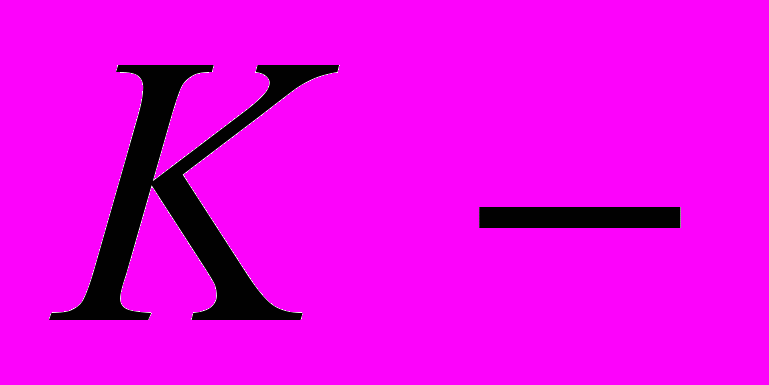групп для основных классов 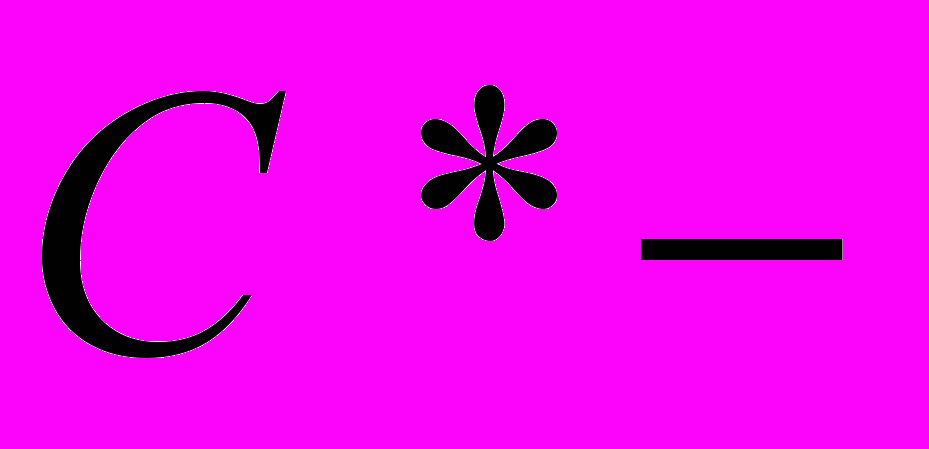алгебр.

^ 3. Операторная 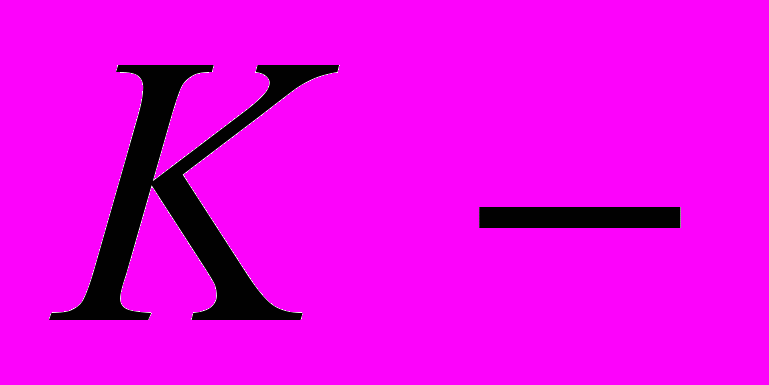теория.

1. Фредгольмовы представления и 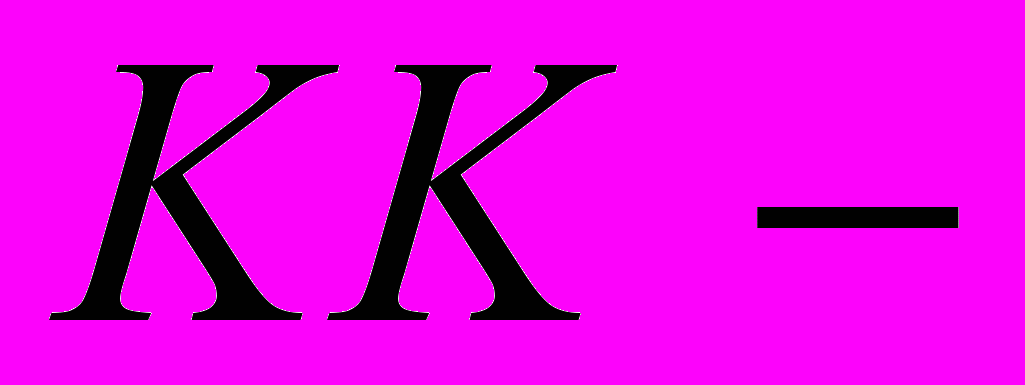функтор Каспарова. Определе­ние и основные свойства.

2. Эквивалентность различных определений 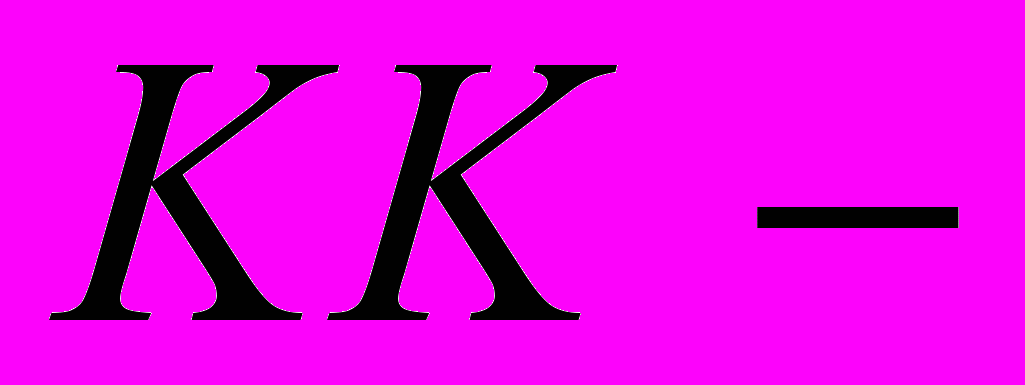функтора (гомотопии и опера­тор­ные гомотопии).

3. Техническая теорема Каспарова. Произведение-пересечение.

4. Описание Кунца для 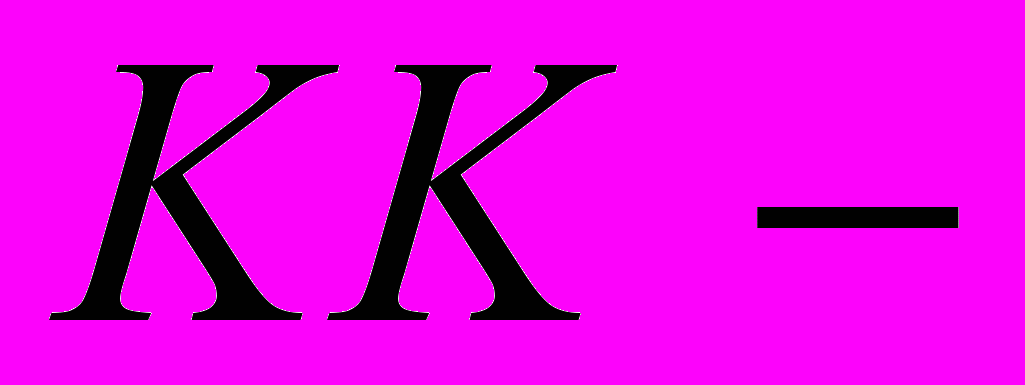теории.

5. Неточность 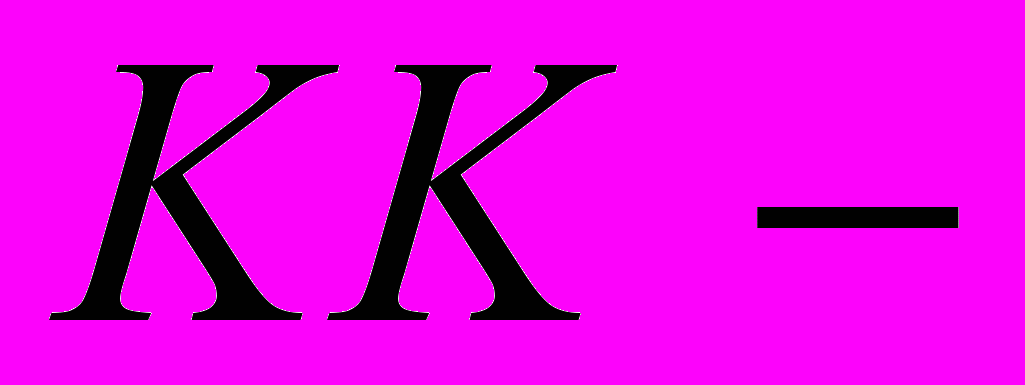функтора,. Контрпример Скандалиса.

6. Асимптотические гомоморфизмы 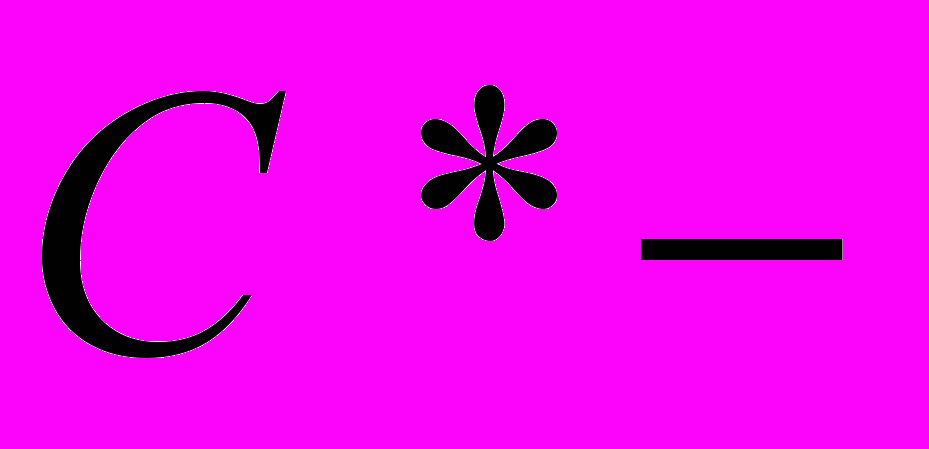алгебр. Пример матриц Войкулеску.

7. Определение 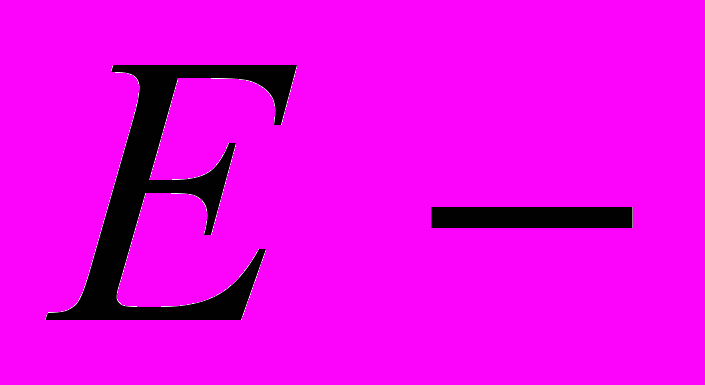теории Конна-Хигсона. Связь ее с 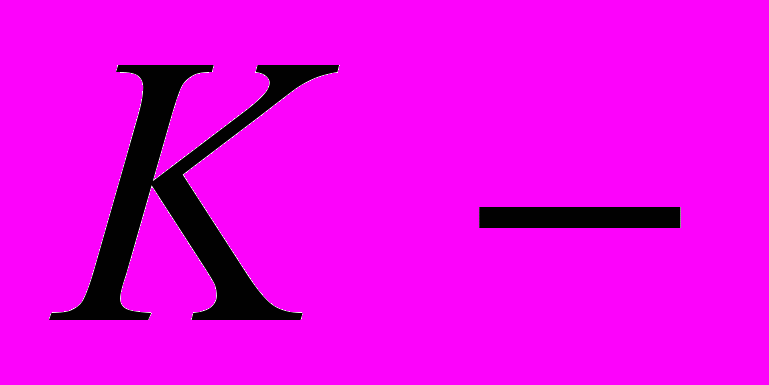и 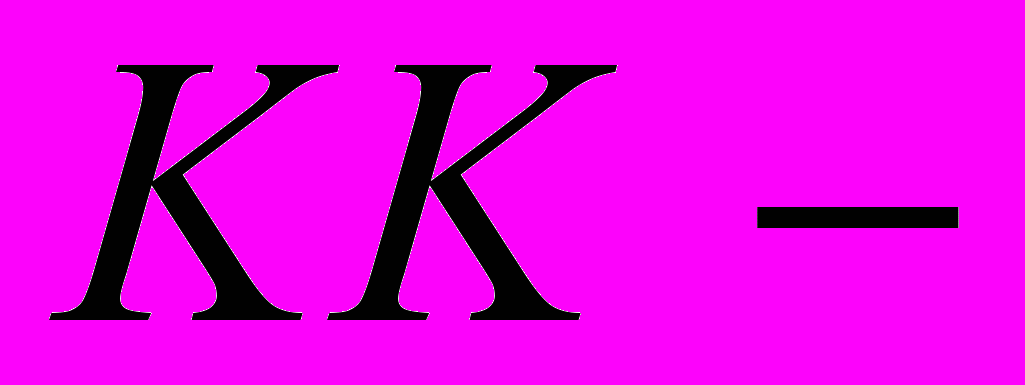теорией.

8. Точность и периодичность Ботта для 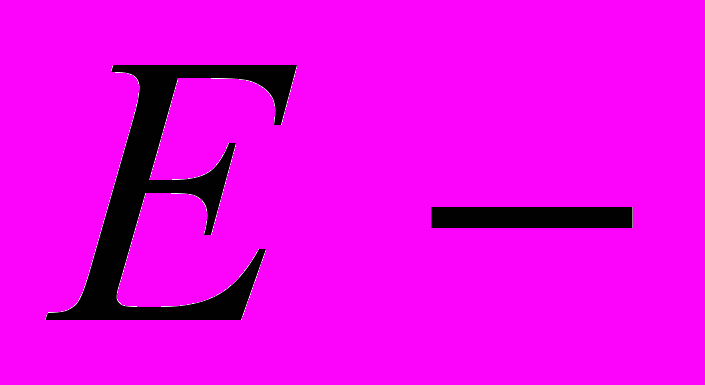теории.

^ 4. Циклические (ко)гомологии.

1. Определение, основные свойства, бикомплексы.

2. (Ко)гомологии де Рама топологических алгебр. Связность на гиль­бертовом модуле. Связь с классической дифференциальной геоме­трией.

3. Гомологии с внутренними симметриями.

4. Характер Чженя.

^ 5. Эллиптические операторы и теоремы об индексе.

1. Струи, дифференциальные операторы.

2. Пространства Соболева, теоремы вложения.

3. Алгебра Сили, псевдодифференциальные операторы.

4. Изоморфизм Тома.

5. Аналитический и топологический индекс.

6. Аксиоматический подход.

7. Примеры: операторы Лапласа, Хирцебруха, Дирака.

8. Теорема об индексе.

9. 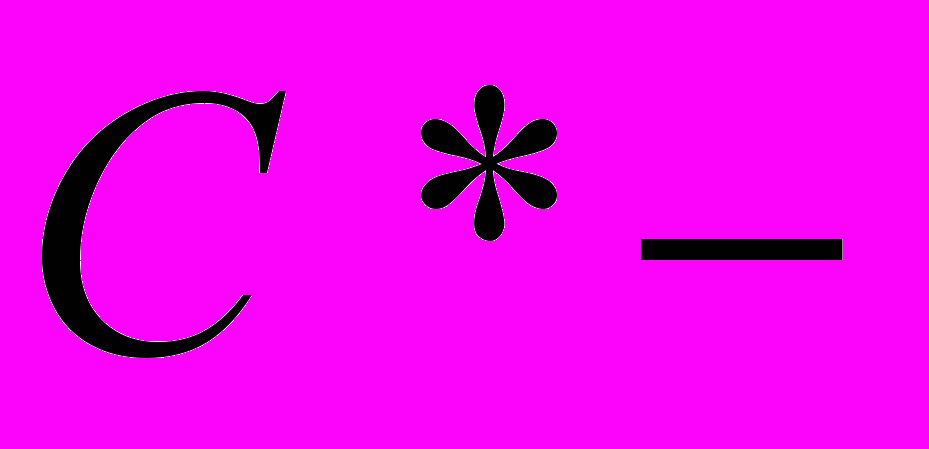теорема об индексе.

10. Изоморфизм Тома-Конна-Фака-Скандалиса. 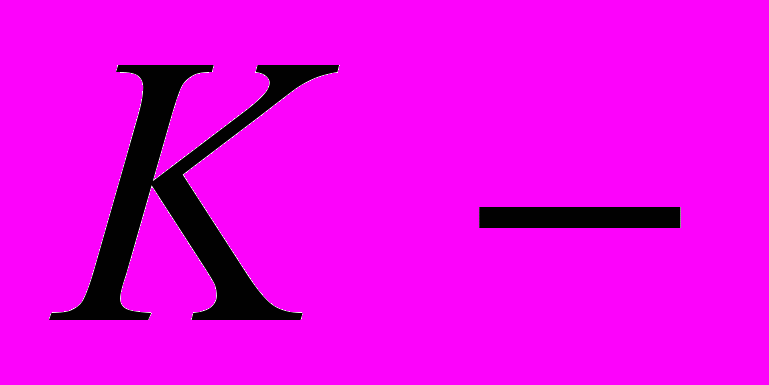гомологическая теорема об индексе.

11. Алгебраическая теорема об индексе.

^ 6. Приложения некоммутативной геометрии к задачам топологии и геометрии.

1. Фундаментальная группа и инварианты многообразий, связанные с фундаментальной группой. Алгебраические комплексы Пуанкаре.

2. Высшие сигнатуры. Каноническое расслоение Мищенко как элемент 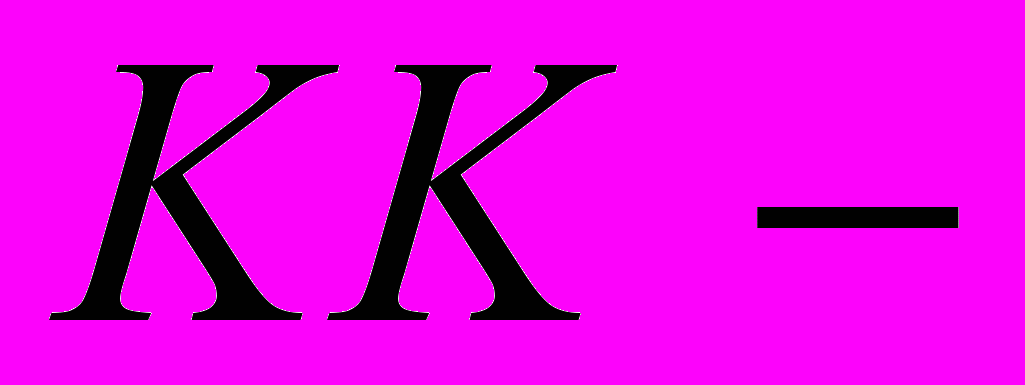группы. Гипотеза Новикова.

3. Аменабельные и гиперболические группы.

4. Теорема Конна-Московичи.

5. Кривизна и гипотеза Громова-Лоусона-Розенберга.

6. Гипотеза Баума-Конна.

7. 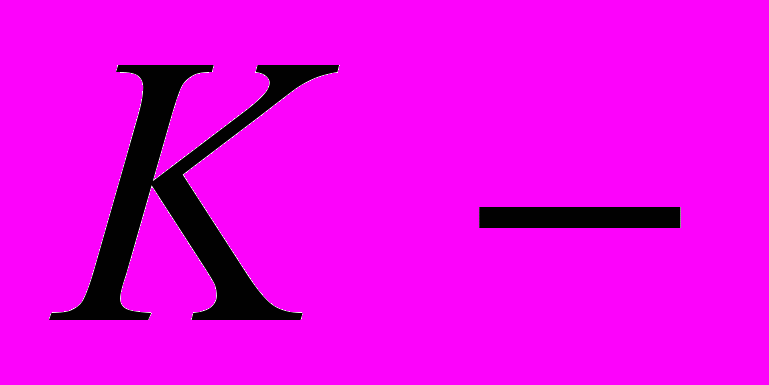аменабельность и другие свойства.

8. Структура орбит и модули.

9. Некоммутативный гармонический анализ и числа Раидемайстера.

10. Расширения 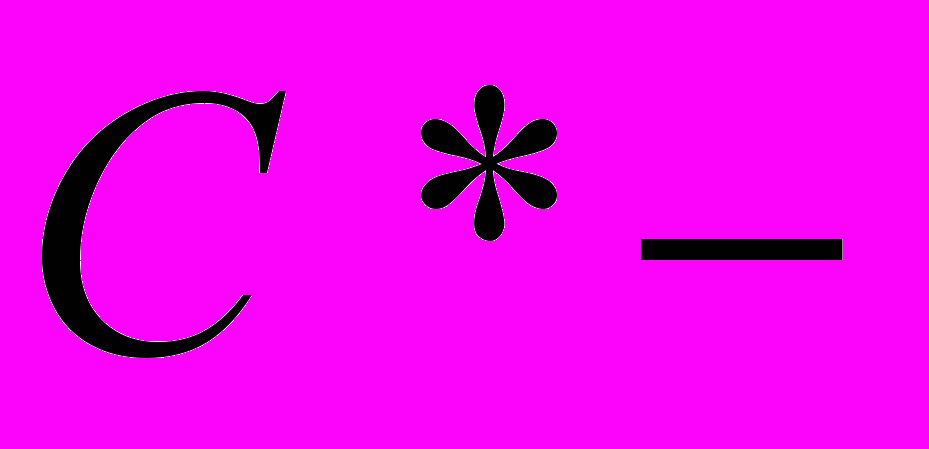алгебр. Теорема Брауна-Дагласа-Филлмора.

11. Классификация расширений 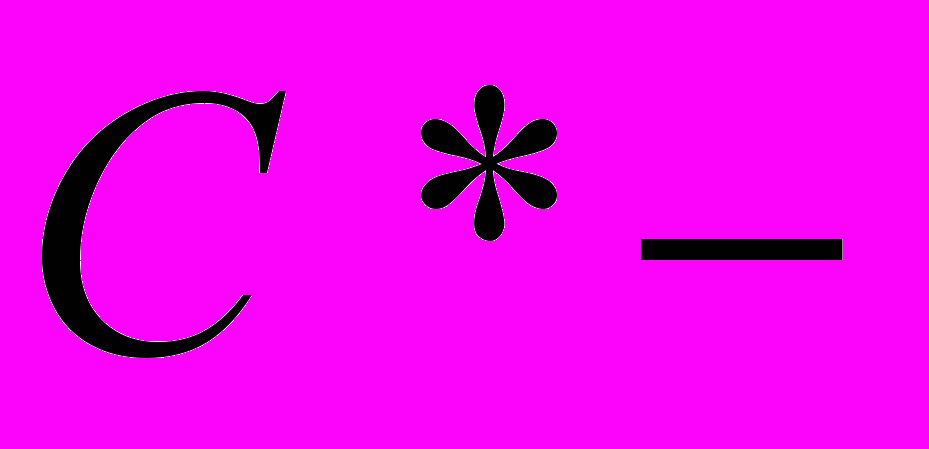алгебр.


Литература

1. Атья М. Лекции по 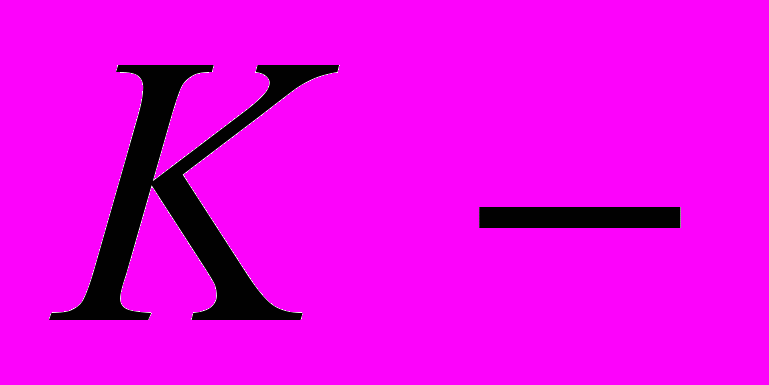теории. М., Мир, 1967.

2. Каруби М. 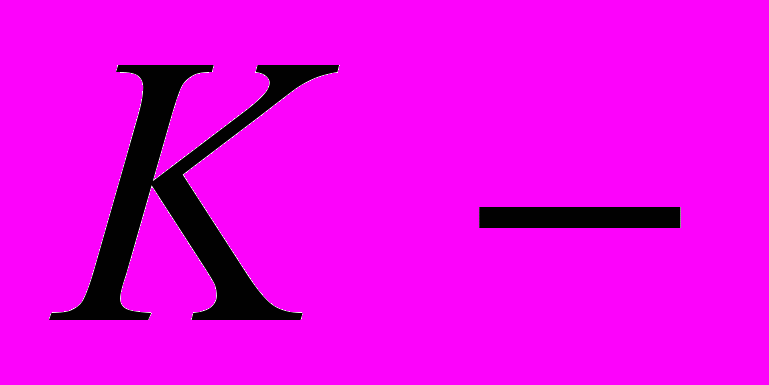теория. М., Мир, 1981.

3. Мануйлов В.М., Троицкий Е.В. 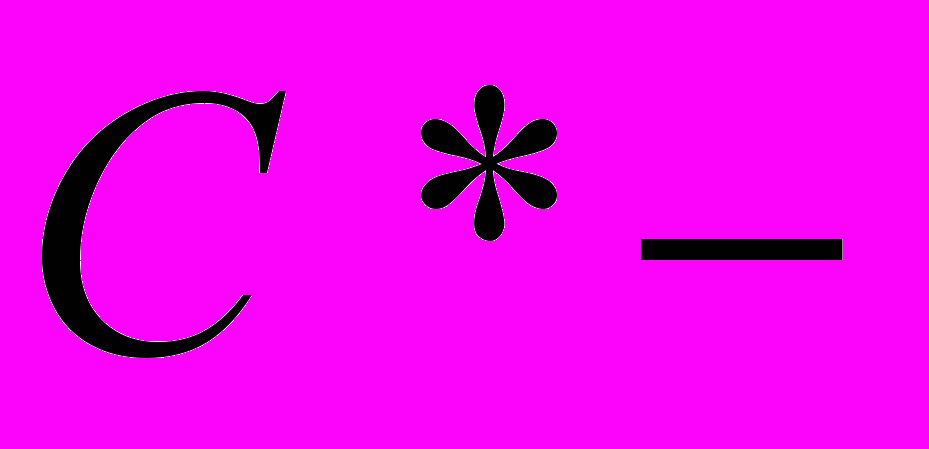гильбертовы модули. М., Факториал, 2001.

4. Мищенко А.С. Векторные расслоения и их применения. М., Мир, 1984.

5. Соловьев Ю.П., Троицкий Е.В. 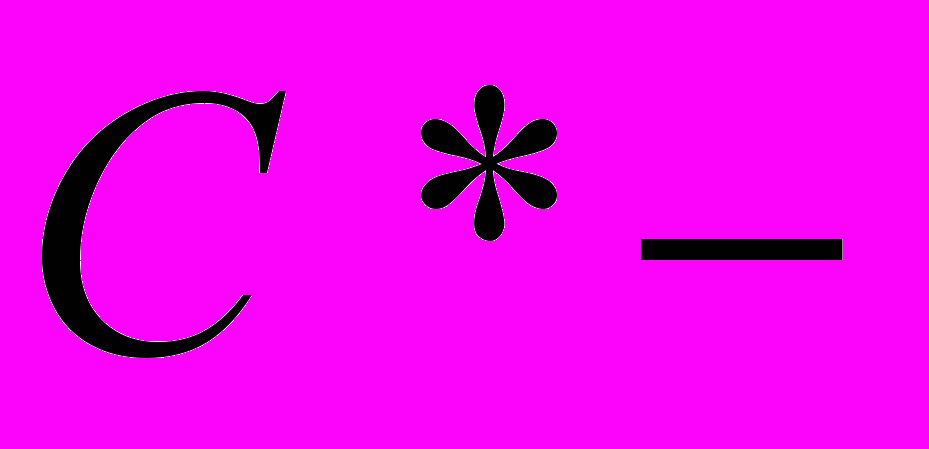алгебры и эллиптические операторы в дифференциальной топологии. М., Факториал, 1996.

6. Хьюзмоллер Д. Расслоенные пространства. М., Мир, 1970.

7. Loday J.-L. Cyclic homology. Springer, Berlin, 1992.

8. Connes A. Noncommutative Geometry. Academic Press, 1994.

9. Karoubi M. Homologie cychque et 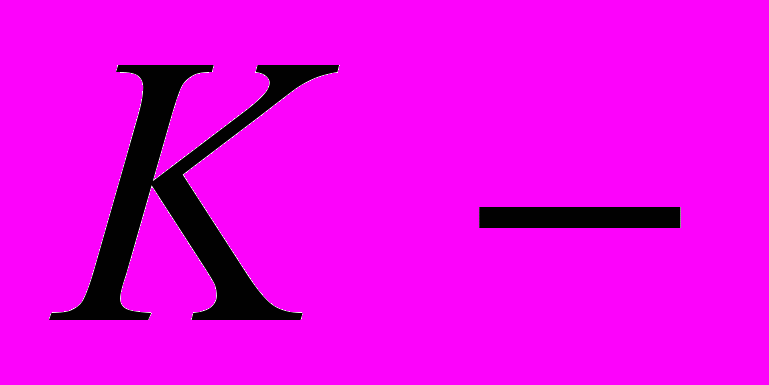théorie. Astérisque № 149, 1987.

10. Jensen, Thomsen K. Elements of 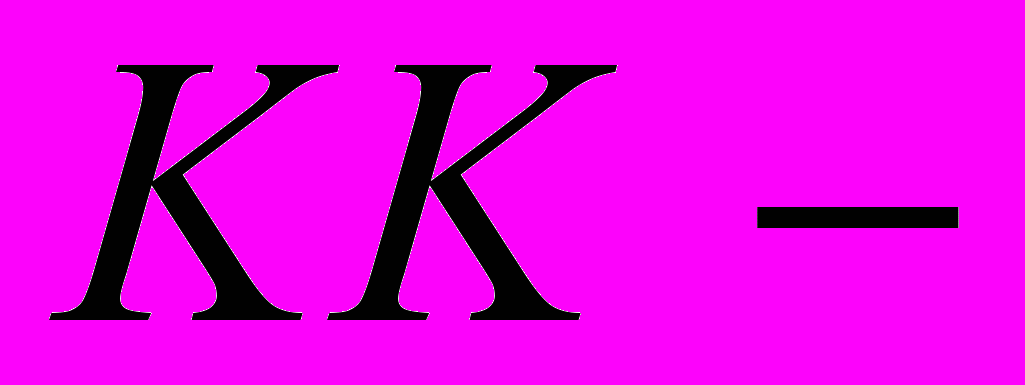theory.