Geum.ru

Программа «Живая геометрия»

Вид материалаПрограмма

Содержание


Точка готовальни (рис. 1) строится три произвольные точки. С помощью инструмента Текст
Подобный материал:
ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ «ЖИВАЯ ГЕОМЕТРИЯ» ПРИ ДОКАЗАТЕЛЬСТВЕ ТЕОРЕМ

Программа «Живая геометрия» является электронным аналогом готовальни с дополнительными динамическими возможностями и со стандартными компьютерными функциями типа редактирования, каталогизирования и т.п. Эта компьютерная среда предоставляет пользователю и другие, непривычные пока возможности (например, озвучивание чертежей), которые еще не вошли в педагогическую практику; однако представляются весьма перспективными. «Живая геометрия» позволяет создавать красочные, варьируемые и редактируемые чертежи, осуществлять операции над ними, а также проводить все необходимые измерения. Чертежи можно компоновать в сценарии и своеобразные геометрические мультфильмы.

Программа обеспечивает деятельность учащихся в области анализа, исследования, построений, доказательств, решения задач, головоломок и даже рисования; позволяет обнаруживать закономерности в наблюдаемых геометрических явлениях, формулировать теоремы для последующего доказательства, подтверждать уже доказанные теоремы и развивать их понимание.



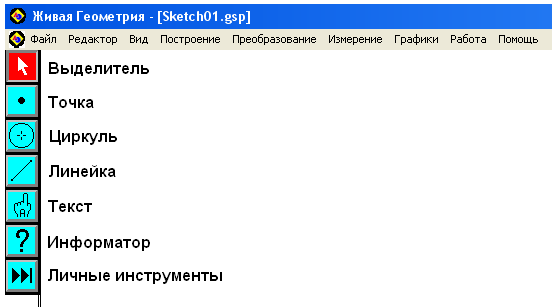
Рис. 1. Готовальня и меню программы «Живая геометрия»

Основные инструменты собраны в готовальне, которая появляется каждый раз с новым чертежом (рис. 1). Это: выделитель, точка, циркуль, линейка, текст, информатор, личные инструменты. Может показаться, что их очень мало, ведь даже в графической панели инструментов текстового редактора MS Word готовых геометрических фигур во много раз больше. Но, с одной стороны, эти инструменты дополняют меню Построение и Преобразование, а с другой, папка личных инструментов каждым пользователем может пополняться своими заготовками: параллелограмм, правильный треугольник, квадрат, серединный перпендикуляр и т.д. Вместе с программой распространяется очень подробное электронное пособие [1] с описанием всех основных возможностей программы, которое позволяет любому пользователю, знакомому с приемами работы в операционной системе Windows разобраться с выполнением необходимых чертежей.

Рассмотрим использование программы «Живая геометрия» при объяснении нового материала, в частности, при рассмотрении теорем. При изучении темы «Задачи на построение» по учебнику А.В. Погорелова [2] второй темой является «Окружность, описанная около треугольника». В рамках данного параграфа рассматривается теорема: «Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон». Т.е. рассматривается одна из так называемых замечательных точек треугольника – точка пересечения серединных перпендикуляров к сторонам треугольника.

Чертеж, иллюстрирующий условие теоремы можно выполнить следующим образом.

С помощью инструмента Точка готовальни (рис. 1) строится три произвольные точки. С помощью инструмента Текст точки обозначаются буквами. Для этого надо просто выполнить щелчок по точке. Для корректировки обозначения можно выполнить двойной щелчок по букве и появится диалоговое окно Переименовать, в котором вводится необходимое обозначение. При этом допускаются обозначения с индексами. Попарно выделяя точки (для этого выполняется щелчок по одной точке и, удерживая клавишу Shift, выполняется щелчок по второй точке; если необходимо снять выделение, то необходимо выполнить щелчок на пустом месте рабочей области программы), в меню Построение выбираем команду Отрезок. Получаем произвольный треугольник АВС (рис. 2).


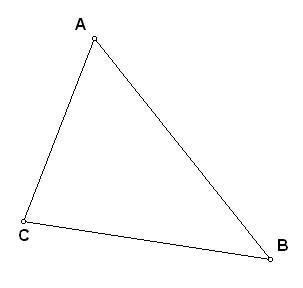Рис. 2.
Рис. 3.


Далее необходимо построить серединные перпендикуляры. Сделать это можно следующим образом. Выделяем отрезок АВ и в меню Построение выбираем команду Точка посередине, затем выделяем построенную середину и отрезок АВ и в меню Построение выбираем команду Перпендикуляр. Аналогично строятся серединные перпендикуляры к остальным сторонам треугольника (рис. 3).

Для достижения цели – построения окружности, описанной около треугольника достаточно построить два перпендикуляра, но построение третьего перпендикуляра позволяет учащимся наглядно убедиться в том, что все три серединных перпендикуляра пересекаются в одной точке. Дополнить эту иллюстрацию можно, перемещая вершины треугольника, – в любом положении вершин серединные перпендикуляры пересекаются в одной точке. После такого наглядного эксперимента у учащихся не останется сомнений в истинности существования рассматриваемой замечательной точки треугольника. Останется только доказать это строго, чему также может способствовать использование «подвижного» чертежа в программе. Ниже мы рассмотрим эту ситуацию подробнее.

С методической точки зрения возникает вопрос, когда целесообразно выполнять это построение: прямо на уроке на глазах учащихся или заблаговременно перед уроком? Очевидно, что первый вариант произведет больше положительного воздействия на учащихся, но если не будет потрачено неоправданно много времени, поэтому предварительно нужно потренироваться (выполнить построение до указанного этапа можно за 1 минуту, т.е. это время сравнимо со временем выполнения чертежа на доске). Но для подстраховки от непредвиденных ситуаций, желательно иметь готовый чертеж и выбор осуществить непосредственно на занятии в зависимости от сложившейся педагогической ситуации.

Развивая идеи наглядного построения в программе можно предложить следующие эксперименты с чертежом:

– переместить вершину А так, чтобы точка пересечения серединных перпендикуляров находилась вне треугольника (рис. 4);

– перемещать вершину А дальше, пока она не попадет на прямую ВС и точка пересечения пропадет – серединные перпендикуляры будут параллельны, но и треугольника не будет – вырожденный случай (рис. 5);


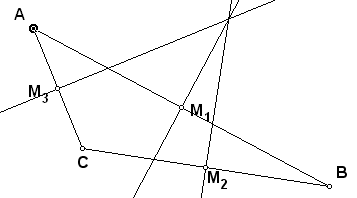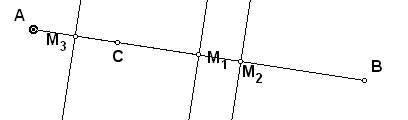Рис. 4.
Рис. 5.

– перемещать вершину А дальше и получить точку пересечения с другой стороны треугольника (рис. 6).

При выполнении этих манипуляций рекомендуется сохранять разные версии-состояния чертежа, чтобы можно было в любой момент времени открыть удобный для экспериментов вариант или начинать каждый новый эксперимент «сначала». Так рекомендуется сохранить вариант, изображенный на рис. 3.


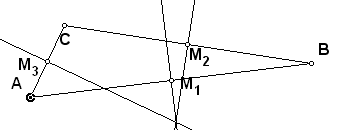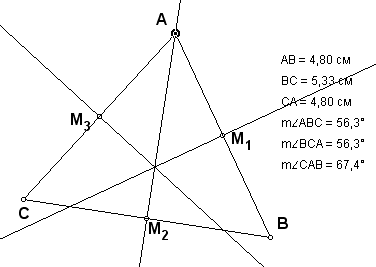Рис. 6.
Рис. 7


Для дальнейших манипуляций с чертежом можно использовать возможность выполнения программой измерений расстояний между точками, определение градусной меры углов и т.п.

Определим размеры сторон треугольника и величины его углов. Для этого выделим точки А и В, в меню Измерение выберем пункт Расстояние. Появится текст АВ = 6,03 см (на самом деле для каждого чертежа эта величина будет своя, такой размер отрезка получился у автора). Этот текст можно расположить в удобном месте окна. Аналогично предлагается определить размеры остальных сторон треугольника. Далее определим размеры углов. Для этого последовательно выделяем точки С, А, В и в меню Измерение выбираем команду Угол. Появится текст с величиной угла. Аналогично выделяем остальные углы треугольника и определяем их градусные меры. Хочется отметить, что обозначение угла происходит по правилам принятым в геометрии, т.е. если выбираем угол А и хотим его обозначить тремя точками, то буква А должна располагаться посередине. Если просто выделить точку А, то команда Угол меню Измерение будет недоступна.

После этого можно продолжить эксперименты с чертежом и рассмотреть некоторые частные случаи расположения точек, которые позволят повторить некоторый геометрический материал и провести пропедевтику некоторых свойств треугольника. Можно предложить следующие эксперименты с чертежом:

– помещаем точку А на серединный перпендикуляр к стороне ВС (рис. 7); получится равнобедренный треугольник и это наглядно видно по размерам сторон АВ и СА; можно задать школьникам вопросы: «какой треугольник получился?», «какое свойство равнобедренного треугольника объясняет такую ситуацию?», «как нужно перемещать вершины исходного треугольника, чтобы получился равнобедренный треугольник?», «что будет, если вершину В поместить на серединный перпендикуляр к стороне АС?»;

– помещаем вершину В на серединный перпендикуляр к стороне АС (рис. 8); точно это сделать достаточно сложно при описанном способе выполнения чертежа, но хорошее приближение получить не трудно; учащиеся увидят, что все стороны примерно равны и все углы примерно равны 600; недостаток приближенного равенства оправдан выполнением манипуляций именно на уроке – чтобы не тратить время урока на «прицеливание»; если быть предусмотрительным, то можно соответствующее положение чертежа подготовить заранее и учащимся показать готовое, с точным равенством всех элементов треугольника;


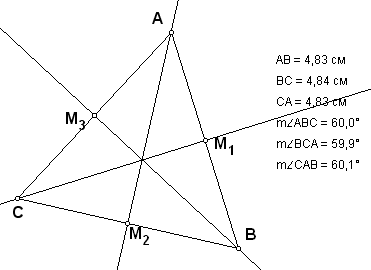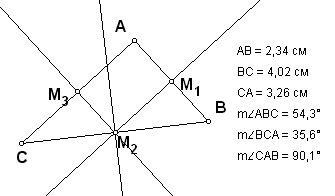Рис. 8
Рис. 9


– перемещаем вершину А так, чтобы точка пересечения перпендикуляров совпала с серединой стороны ВС – точкой М2 (рис. 9); в этом случае имеем прямоугольный треугольник, что видно по измерению угла САВ; примерное равенство объясняется также как и в предыдущем случае; здесь можно обратить внимание школьников на технические детали выполнения этой процедуры: можно ли добиться совпадения точек перемещая одну вершину, или необходимо манипулировать несколькими вершинами? Ответ на этот вопрос связан с существенным свойством прямоугольного треугольника, объясняющим этот факт – в прямоугольном треугольнике с любой гипотенузой центр описанной окружности совпадает с серединой гипотенузы.

После таких манипуляций необходимо вернуться к содержанию рассматриваемой теоремы и построению чертежа до конца. Надо отметить, что выполнение всех описанных выше процедур с чертежом зависит от педагогической ситуации и является необязательным, главный критерий – время, которое согласно плана урока можно потратить на работу с этим чертежом не в ущерб достижения дидактических целей занятия, ну а также обращать внимание на то, как реагирует аудитория. Мало того, описанные эксперименты с чертежом можно проводить в любом месте занятия – например, если осталось время в конце урока, а может быть после разбора теоремы.

Для продолжения работы целесообразно открыть чертеж, изображенный на рисунке 3 (ранее было рекомендовано его сохранить). Это лишний раз подчеркивает определенную независимость описанных выше экспериментов с чертежом от содержания теоремы.

Теперь можно сообщить школьникам, что для построения описанной около треугольника окружности достаточно двух серединных перпендикуляров, ведь они однозначно определяют центр описанной окружности. Поэтому один перпендикуляр на чертеже можно скрыть. Для этого выделяем перпендикуляр к АС и в меню Вид выбираем пункт Спрятать Линия (или нажать Ctrl + H). Точно также можно скрыть точку М3. Далее необходимо изобразить центр описанной окружности: выделяем перпендикуляры и в меню Построение выбираем команду Точка на пересечении. С помощью инструмента Текст обозначим ее О (см. рис. 10). Осталось построить окружность: выделяем точку О и одну из вершин треугольника, например, А, в меню Построение выбираем команду Окружность по центру и точке.





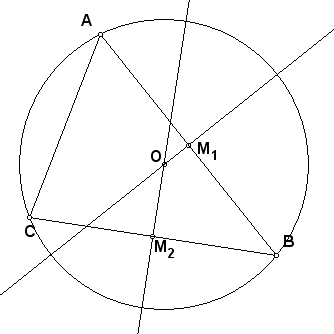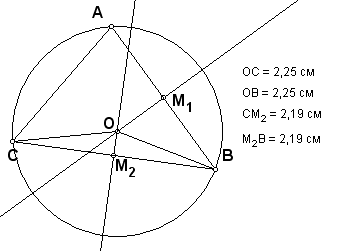Рис. 10
Рис. 11


Для разбора доказательства теоремы следует акцентировать внимание учащихся на том, что посылкой теоремы является данный центр описанной окружности и нужно доказать, что через него проходят серединные перпендикуляры к сторонам. Ведь после выполнения построения некоторым учащимся будет казаться, что имеем дело с обратной теоремой: строили серединные перпендикуляры, получили точку пересечения, надо доказать, что это точка – центр описанной окружности. Здесь также уместно перемещая элементы чертежа обратить внимание школьников на то, что окружность в любом случае проходит через вершины треугольника.

Для изложения идеи доказательства можно изобразить радиусы окружности ОВ и ОС, вынести на экран их размеры, а также вынести на экран размеры отрезков СМ2 и М2В (рис. 11). Таким образом, на чертеже наглядно видно (благодаря измерениям), что ОСВ – равнобедренный и что М2 – середина отрезка ВС, т.е. ОМ2 – медиана, а в равнобедренном треугольнике она является высотой. Такие рассуждения помогают «принять» учащимися доказательство теоремы – увидеть его, ведь, как известно «лучше один раз увидеть, чем сто раз услышать». После этого доказательство можно изложить строго, опираясь на готовый чертеж (рис. 11). Чтобы логика рассуждений не потерялась можно доказательство записать схематично:

1) дан АВС, О – центр описанной окружности;

2) ОСВ – равнобедренный, т.к. ОС = ОВ как радиусы;

3) строим М2 – середину ВС; строим ОМ2;

4) ОМ2 – высота, по свойству равнобедренного треугольника;

5) аналогично для ОМ1.

Такую схему или более подробное изложение может быть предложено самыми разными способами – например, в готовом виде на слайде и т.д. После описанной работы с чертежом готовое доказательство не будет казаться учащимся взятым «с потолка».

Литература:

1. Живая геометрия. Учебно-методическое пособие / Под ред. Шабат Г.Б. – М.: Институт новых технологий образования, 2001. – 239 с.

2. Погорелов А.В. Геометрия: Учеб. для 7-11 кл. сред. шк. – М.: Просвещение, 1992. – 383 с.