«Решение задач линейной алгебры. Операции с матрицами»
| Вид материала | Решение |
СодержаниеФункции для работы с матрицами. |
- Операции с матрицами Решение систем линейных уравнений с помощью матриц Операции, 131.32kb.
- Тема: «теория матриц» Основная задача линейной алгебры, 28.88kb.
- Рабочая программа курса «высшая математика (элементы аналитической геометрии и линейной, 67.54kb.
- I. Решение логических задач средствами алгебры логики 22 >II. Решение логических задач, 486.64kb.
- Конспект открытого урока по теме: "Решение логических задач средствами алгебры логики", 93.45kb.
- Тематическийпла н, 46.68kb.
- Аналитическая геометрия с элементами линейной алгебры, 54.48kb.
- Аналитическая геометрия с элементами линейной алгебры, 44.1kb.
- Некоммутативная геометрия, 36.84kb.
- Урока алгебры и информатики «система счисления. Решение задач с помощью квадратных, 98.53kb.
Тема: «Решение задач линейной алгебры. Операции с матрицами».
Matrix – функция для задания матриц
Синтаксис: matrix([17,3],[-8,11]);
Для применения основных операций с матрицами нужно задать две матрицы:

- Поэлементное сложение матриц.
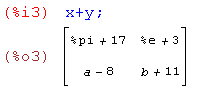
- Поэлементное вычитание матриц.
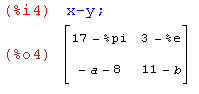
- Поэлементное умножение матриц.

- Поэлементное деление матриц.
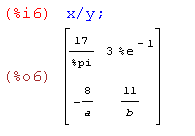
- Поэлементное возведение в степень.
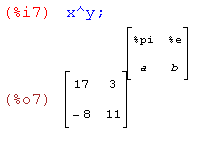
Функции для работы с матрицами.
determinant – нахождение определителя матрицы

eigenvalues – нахождение собственных значений матрицы
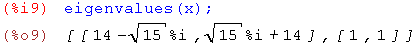
invert – получение обратной матрицы
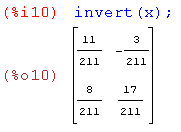
minor – определяет минор матрицы. Первый аргумент - матрица, второй и третий – индексы строки и столбца соответственно

rank – ранг матрицы

submatrix – возвращает матрицу полученную из исходной удалением соответствующих строк и (или) столбцов. В качестве параметров следуют номера удаляемых строк, исходная матрица, номера удаляемых столбцов.

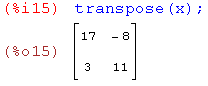
transpose – транспонирование матрицы