Тема: «теория матриц» Основная задача линейной алгебры

Вид материала

Задача

Содержание Элементарными преобразованиями

Подобный материал:

• Рабочая программа курса «высшая математика (элементы аналитической геометрии и линейной, 67.54kb.
• Лабораторная работа 1 Методы решения задач линейной алгебры, 32.21kb.
• Ускорение решения задачи оптимизации дозового распределения при лучевой терапии с применением, 29.69kb.
• Тема: Массивы, 422.12kb.
• Некоммутативная геометрия, 36.84kb.
• Тема Метод Гаусса, 94.48kb.
• Программа школы-конференции «алгебры ли, алгебраические группы и теория, 53.74kb.
• Календарный план учебных занятий по дисциплине "Высшая алгебра и аналитическая геометрия", 94.97kb.
• Теоретический материал дисциплинарного экзамена (бакалавры), 215.88kb.
• Задачи дискретного программирования Постановка проблемы, 14.8kb.

Тема: «ТЕОРИЯ МАТРИЦ»


Основная задача линейной алгебры - решение систем линейных алгебраических уравнений (СЛАУ). Методы решения разнообразны и используют такие понятия, как матрица, определитель и другие. Познакомимся с ними.

Опр. Квадратной матрицей порядка n наз. таблица чисел, состоящая из n строк и n столбцов

= ||a_{i k}|| = A ( 1 )

где 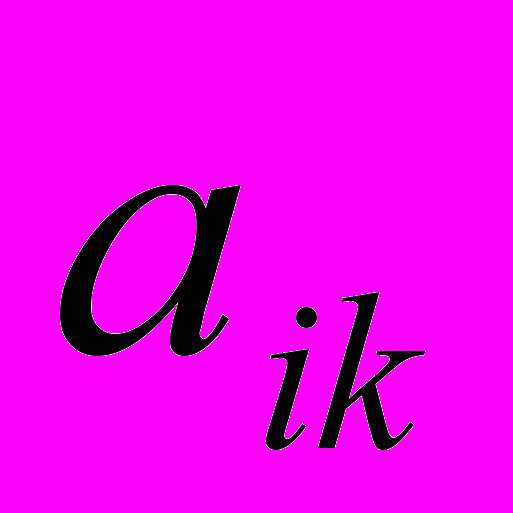- элемент матрицы, индекс i - номер строки, индекс k - номер столбца. Элементы 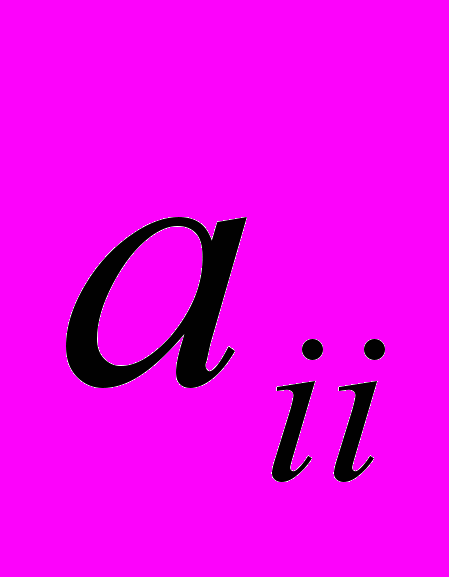наз. диагональными.


Действия над матрицами.

Равенство матриц. Две матрицы одного порядка А = ||а_{i j} || и В = || b_{i j} || равны между собой, если равны их соответствующие элементы а_{i j} = b_{i j} .

Сложение матриц. Суммой матриц одинаковой размерности А = ||а_{i j} || и В = ||b_{i j} || наз. матрица C = || a_{i j} + b_{i j} ||.

Пр. + =

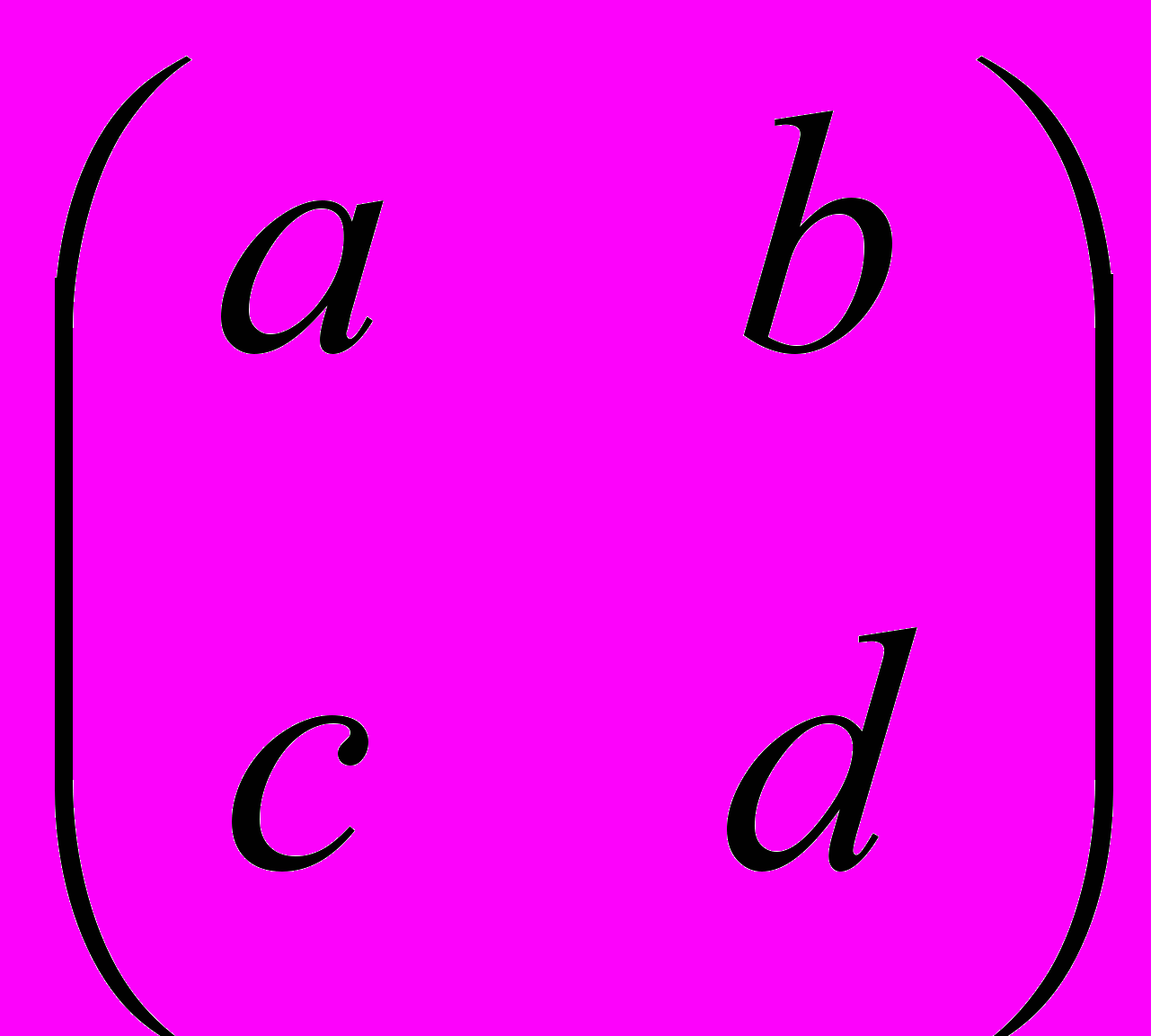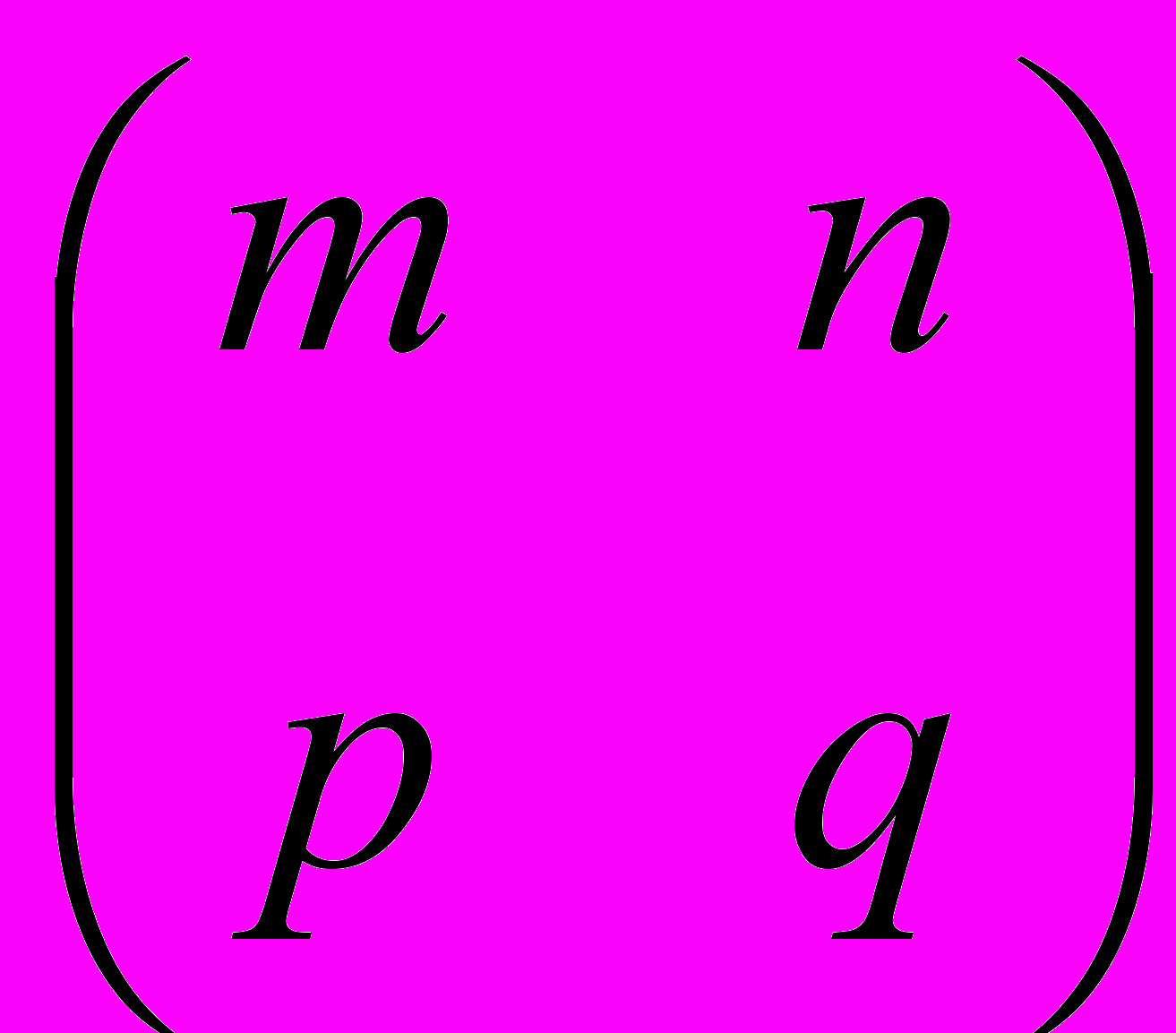Умножение матрицы на число. Произведением матрицы А на число 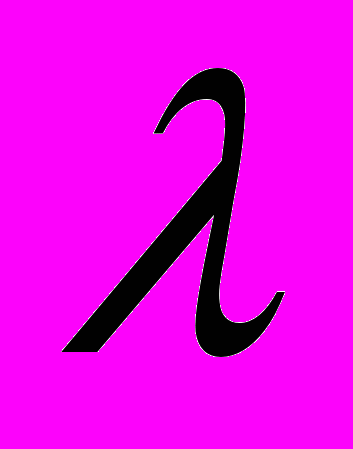наз. матрица

В = 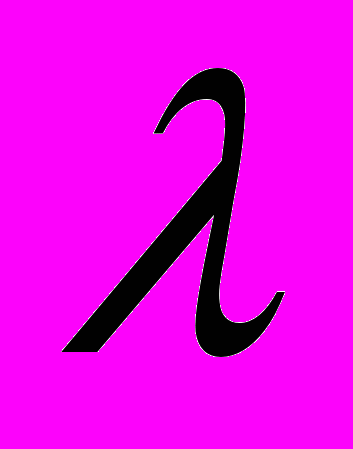А = ||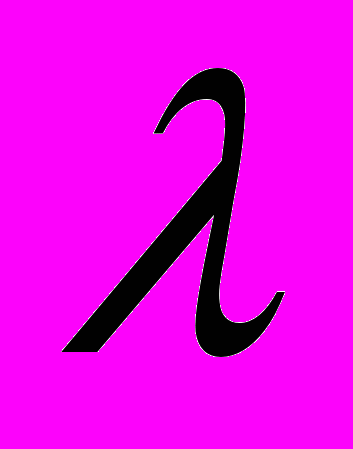а_{i j} ||.

Пр. =

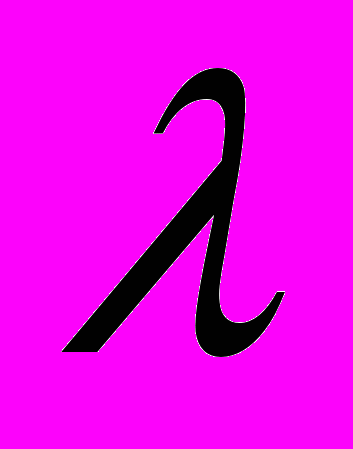
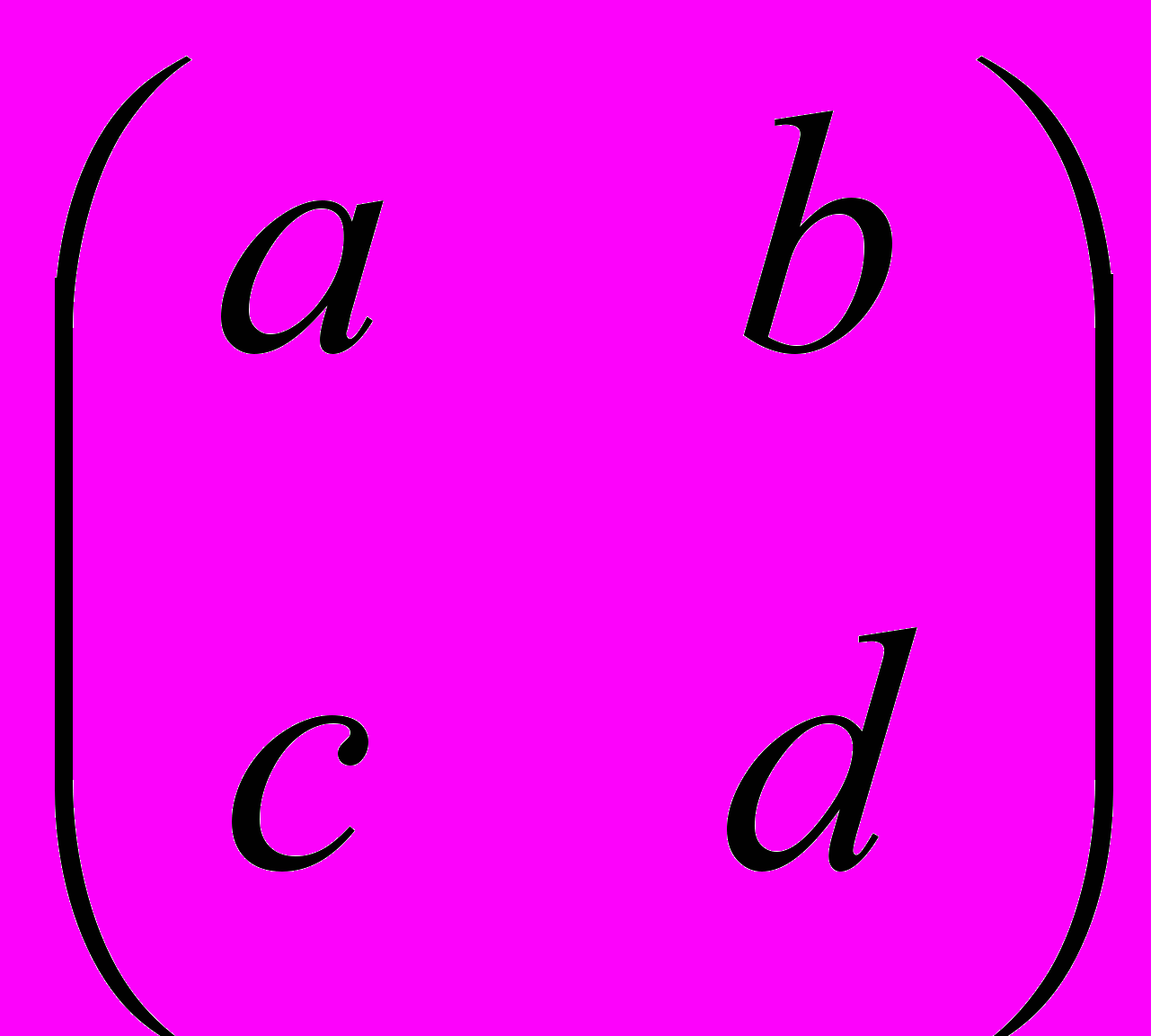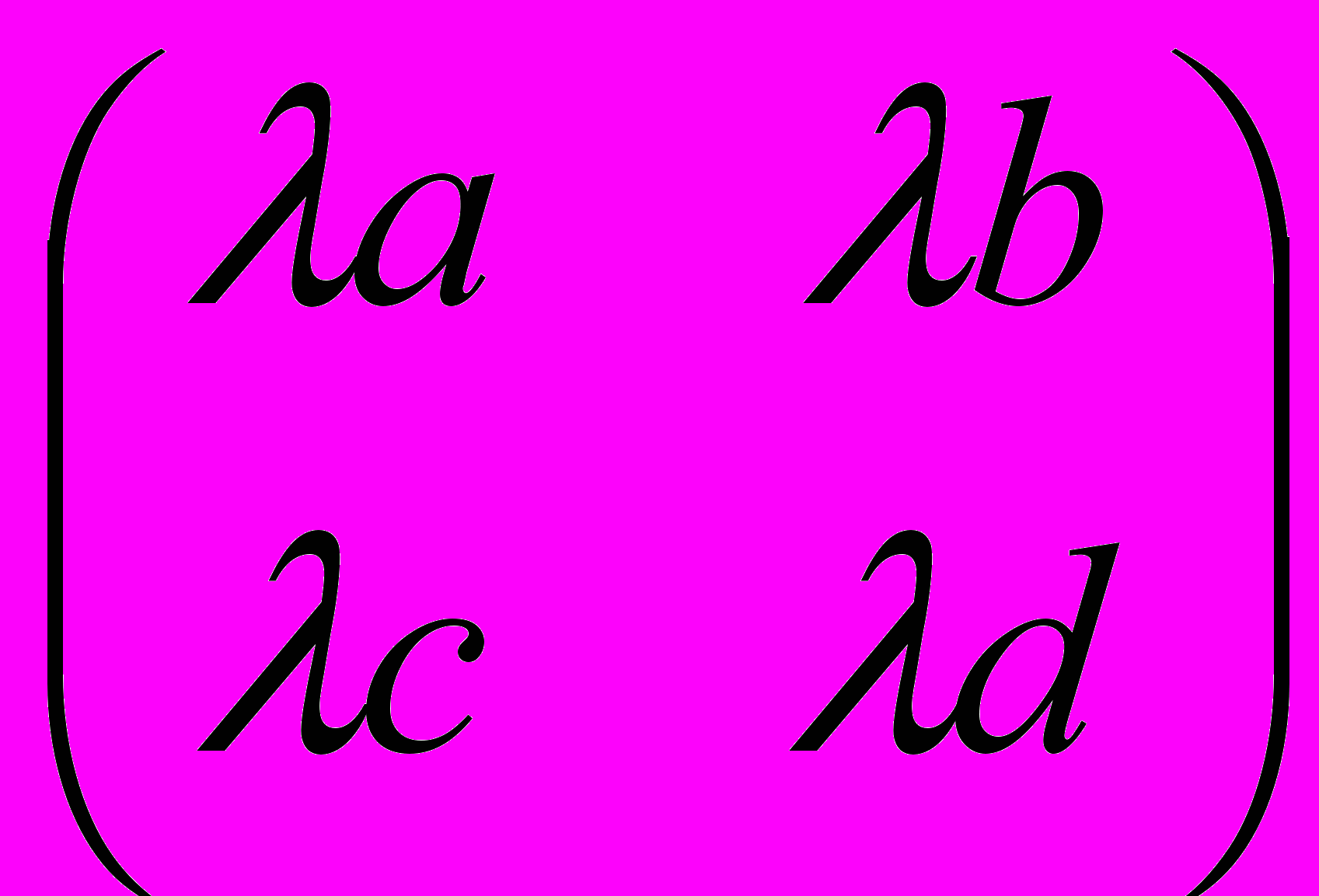
Свойства операции умножения на число.

Пусть А, В – матрицы, ,  – числа.

а) (А + В) = А + В.

б) ( + )А = А + А.

в) ()А = (А).

Умножение матриц одной размерности А и В производится по принципу

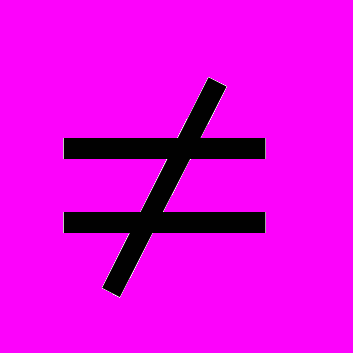«строка на столбец» С = А В = ||a_{i k} b_{k j} ||. Причем, A B B A

Пр. =

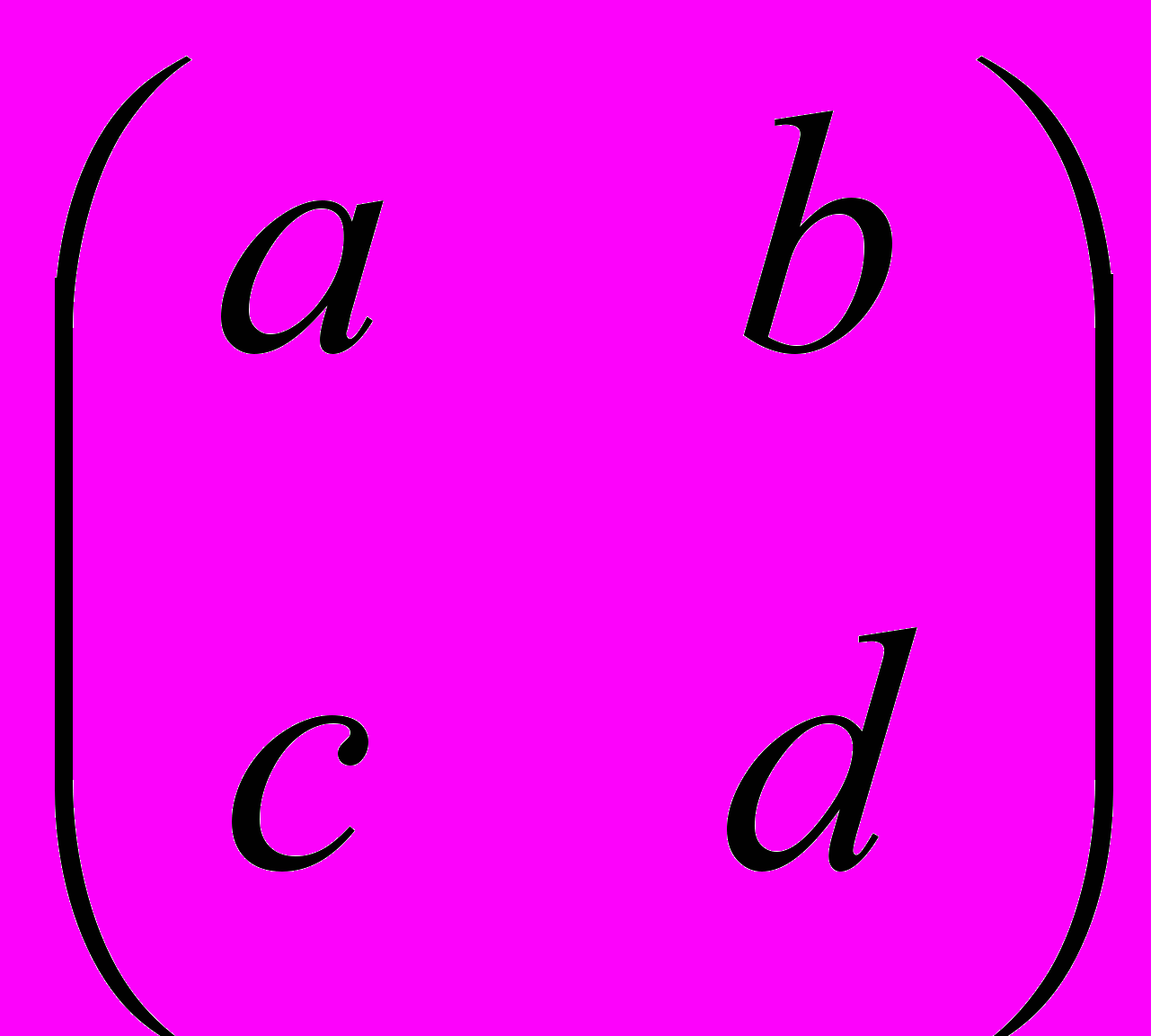
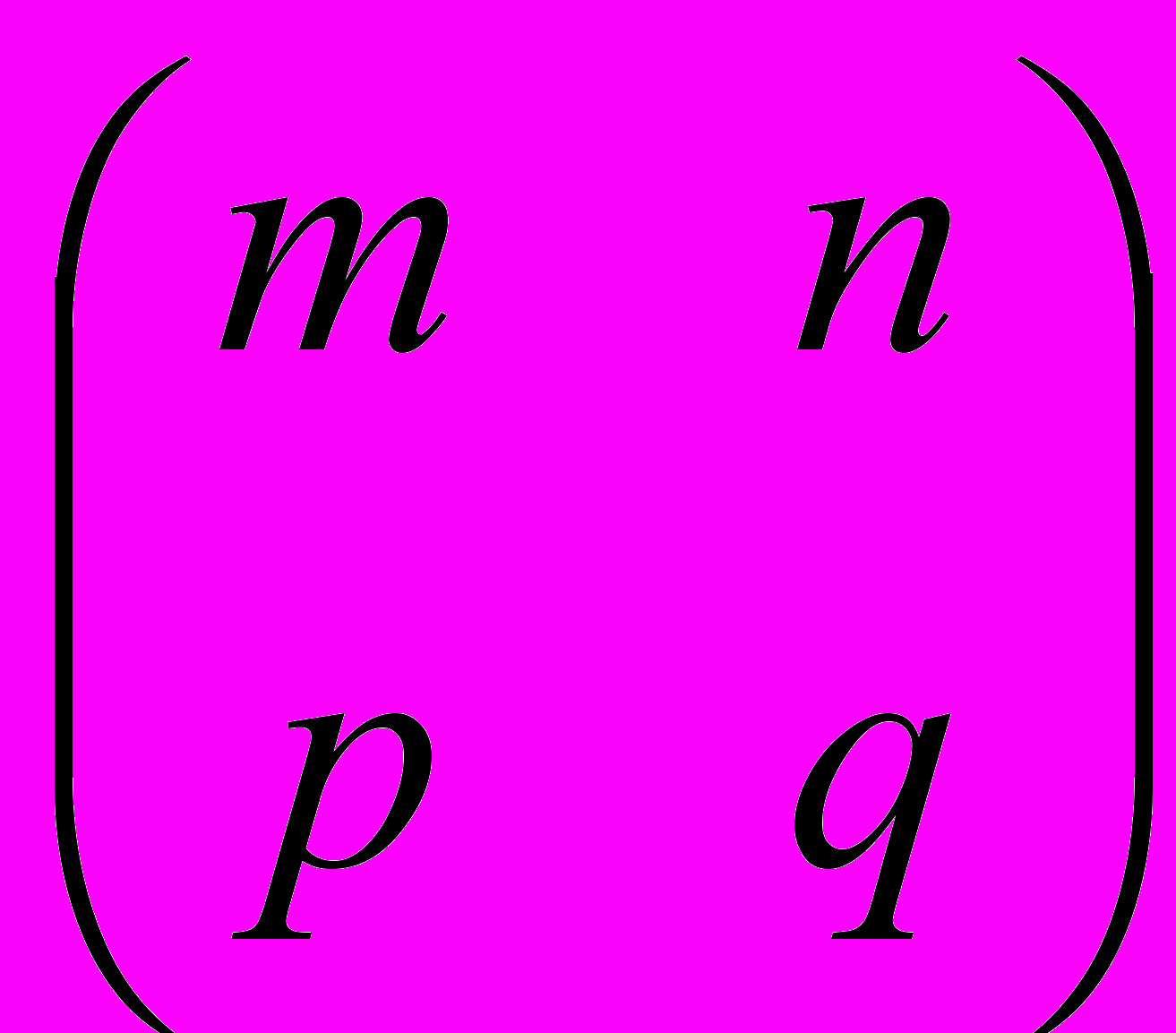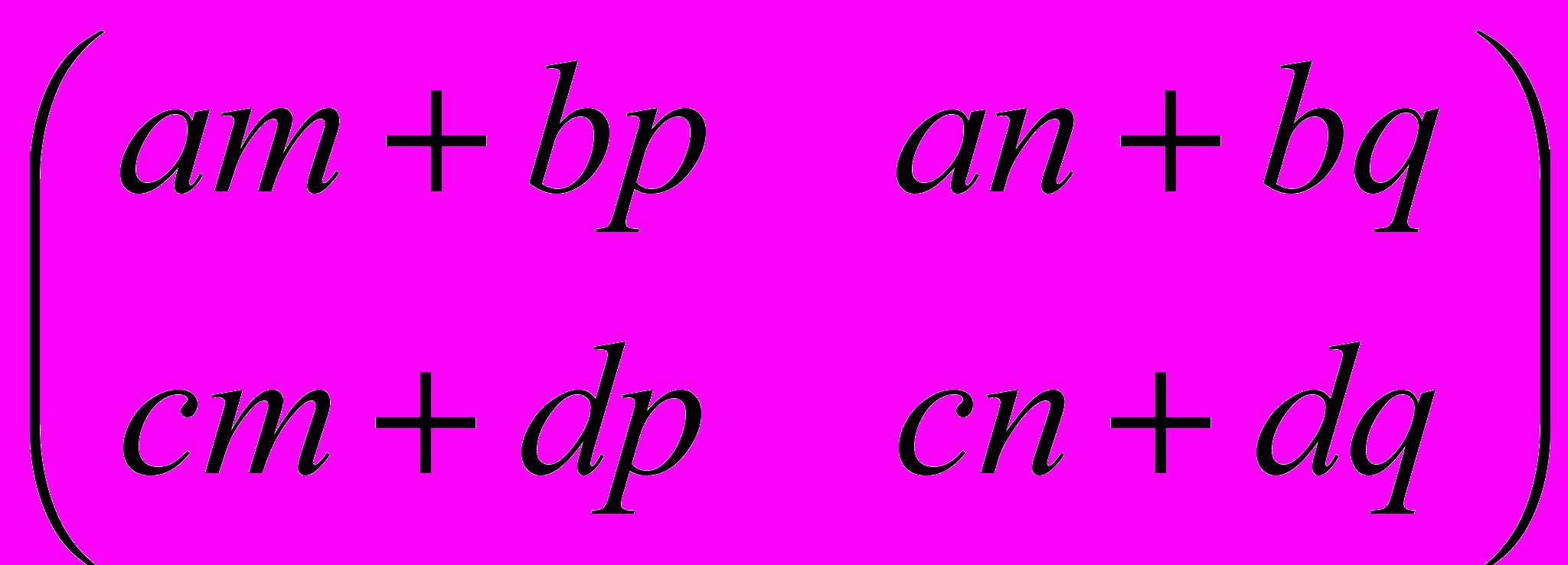
Свойства операции умножения матриц.

а) А0 = 0А = 0.

б) АЕ = ЕА = А.

в) (А+В)С = АС + ВС.

г) А(В + С) = АВ + АС.

д) (АВ)С = А(ВС).


Вектор столбец А и Вектор строка В имеют вид : A = ; B =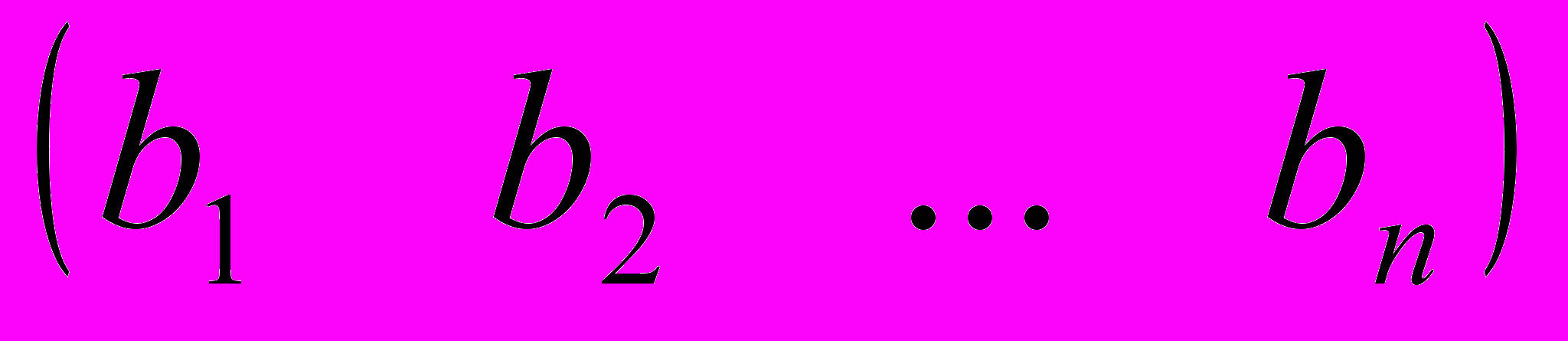

Умножение матрицы А на вектор столбец В порождает новый вектор столбец С и идет по правилу «строка на столбец» ||с_{i ||} = ||a_{i k} b_k ||.

Пр. =


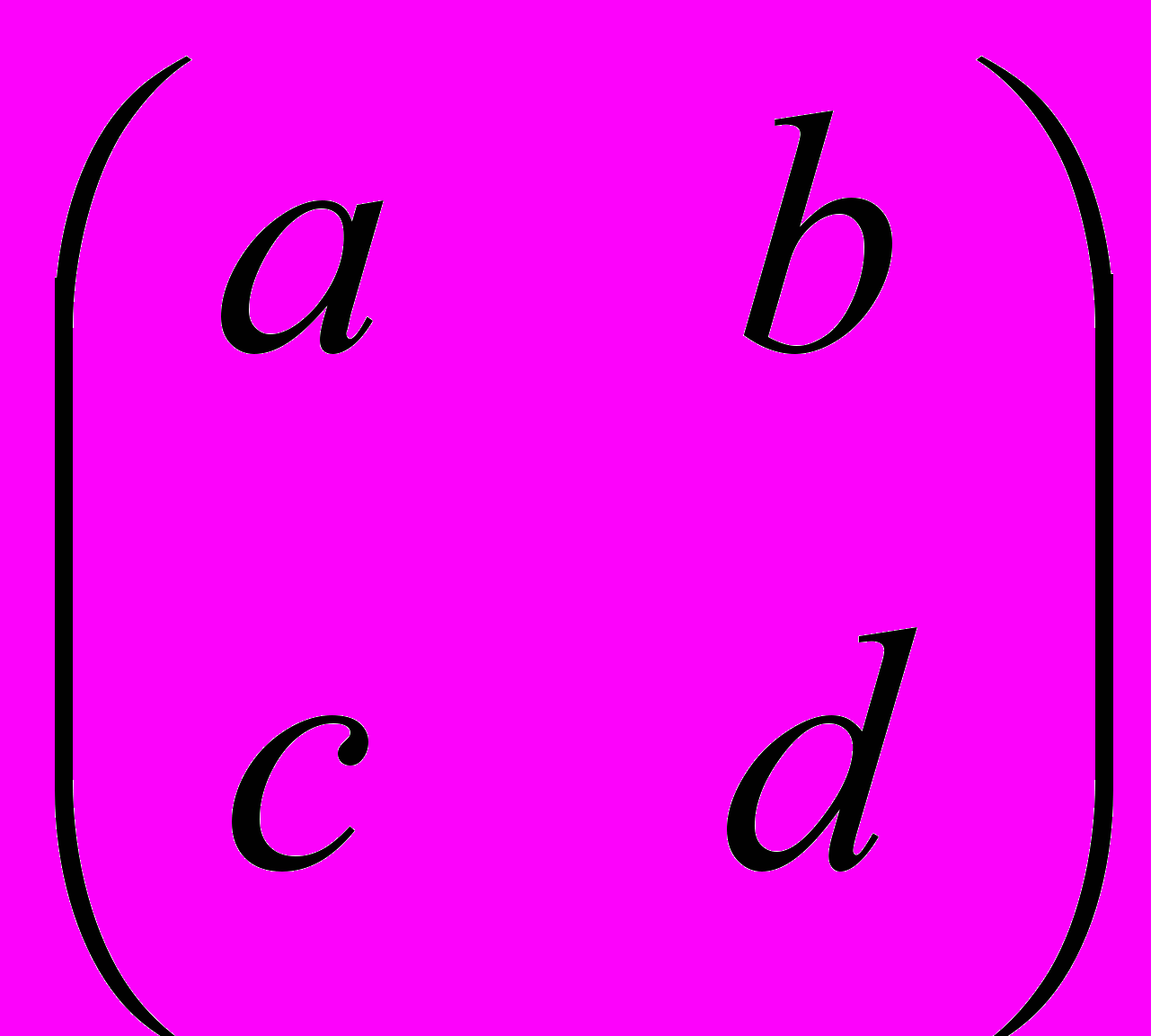
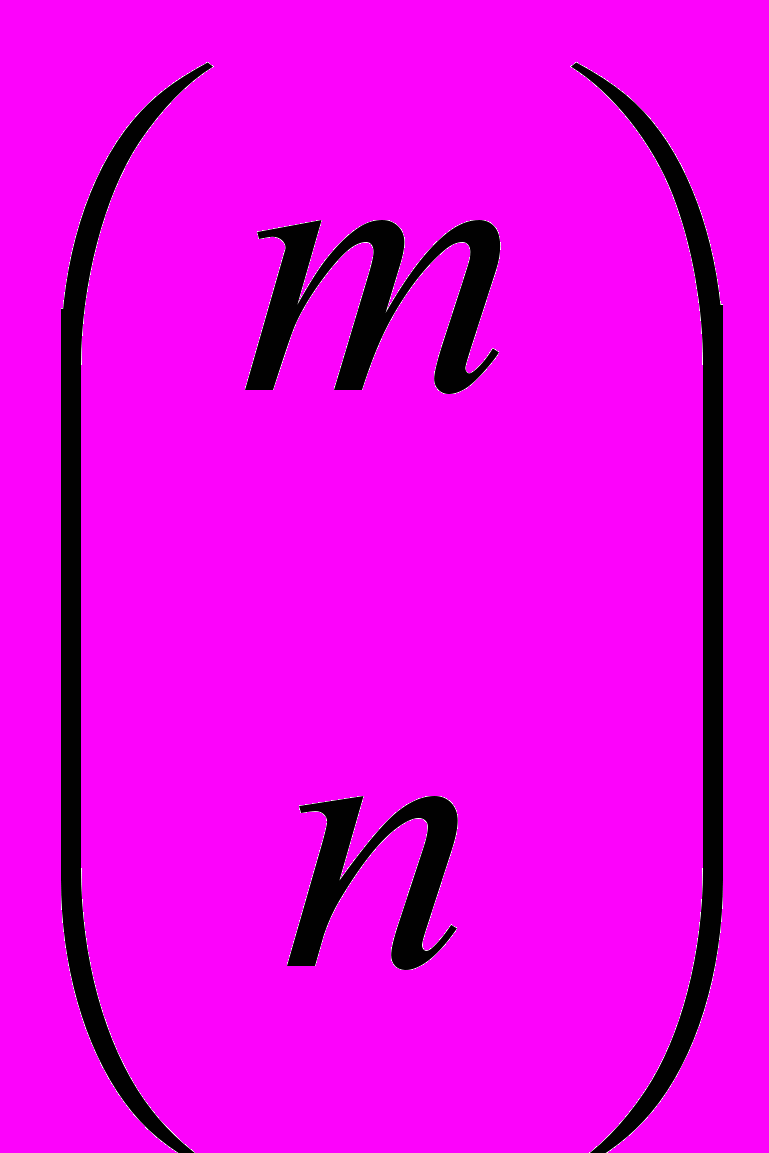Ноль матрица включает только нулевые элементы О = (0).


Единичная матрица Е включает 1 по главной диагонали и 0 в остальных местах.

A E = E A = A . Пр. = =

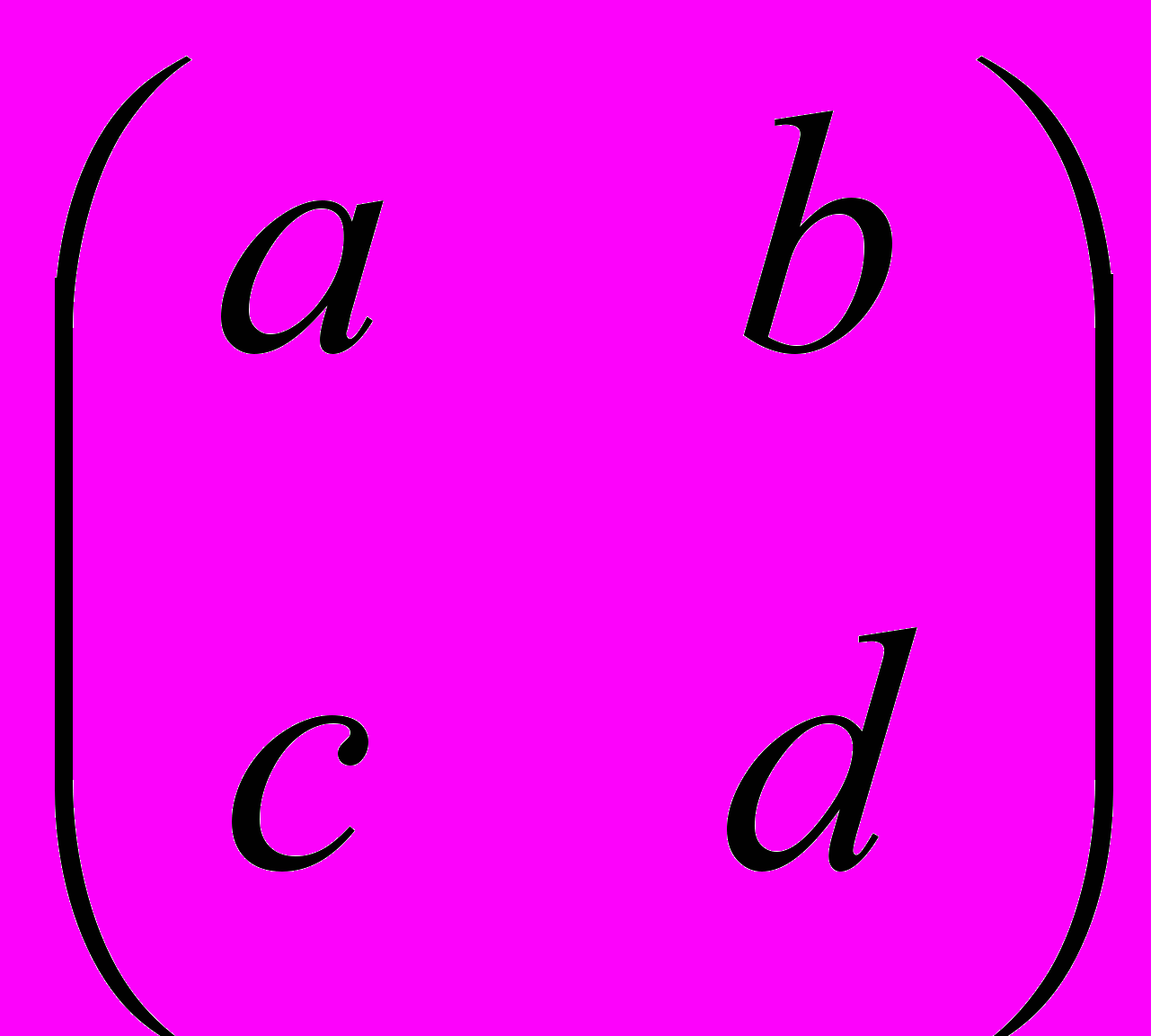
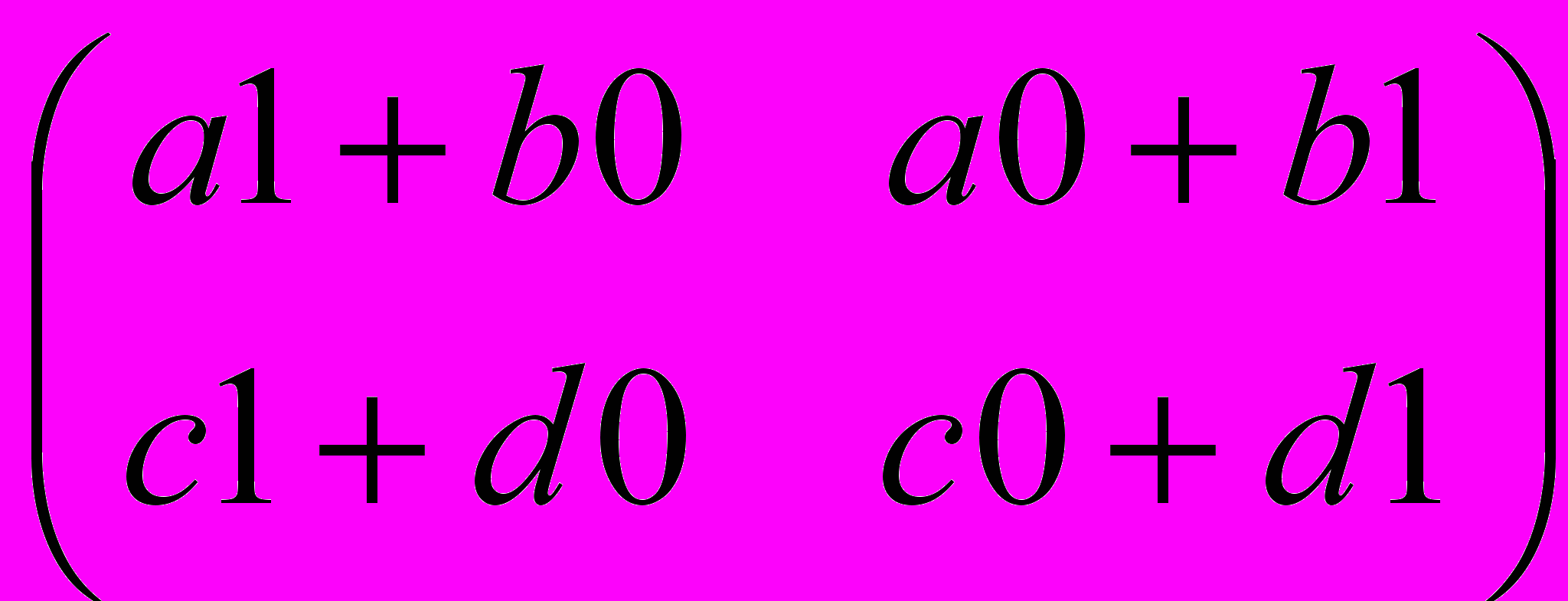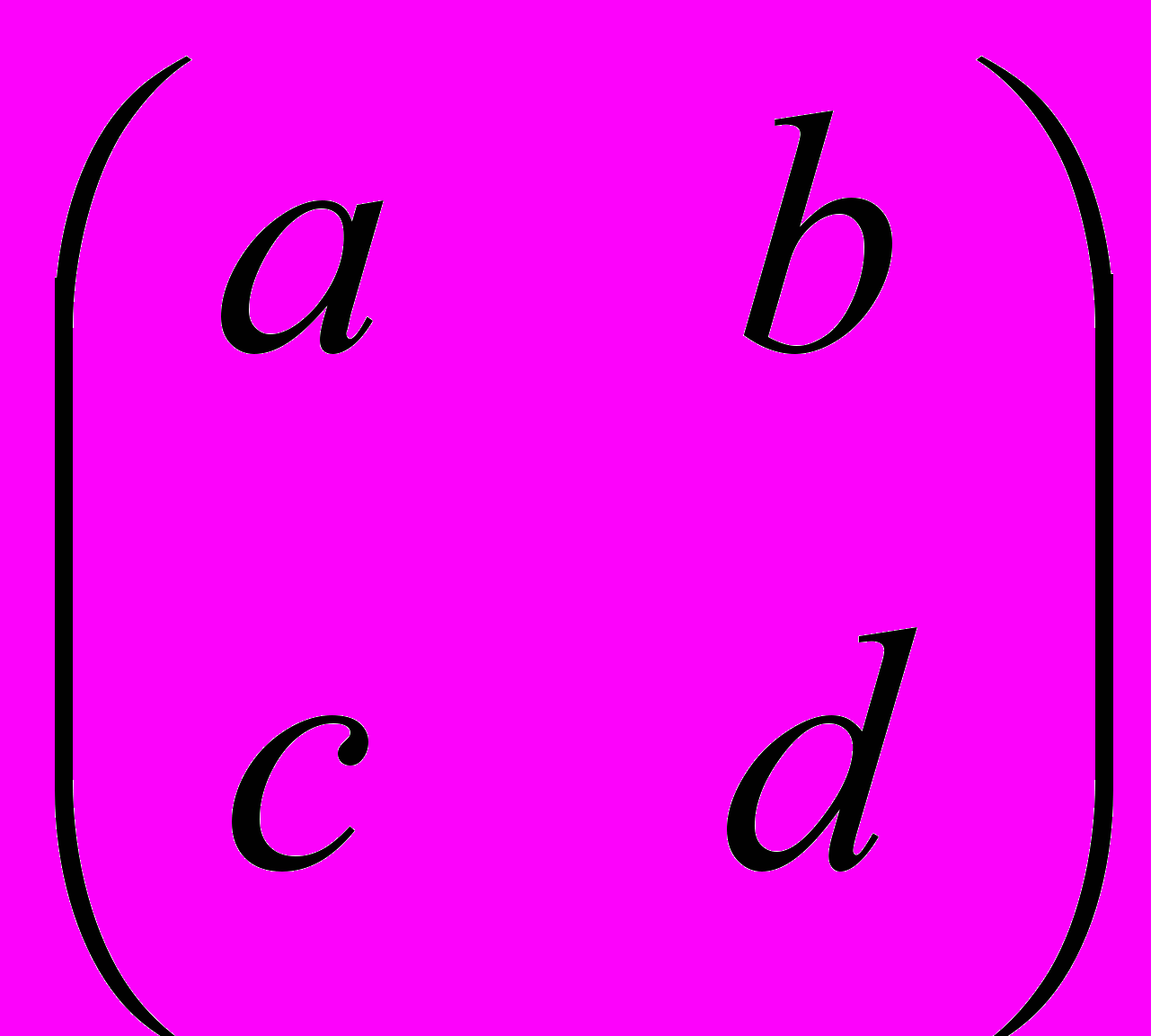
Транспонированая матрица.

Транспонированной матрицей называется матрица, у которой строки заменены соответствующими столбцами. Такая матрица обозначается А^Т. Итак, если А = (a_ij)_mn, то A^T = (a_ji)_nm.

Операция транспонирования обладает свойствами:

а) (А^Т)^Т = А

б) (А + В)^Т = А^Т + В^Т

в) (А)^Т = А^Т, где  – число

г) (АВ)^Т = В^ТА^Т.


Элементарными преобразованиями матрицы называют следующие операции: 1) перестановка строк, 2) умножение любой строки на число, отличное от нуля, 3) сложение строк, 4)отбрасывание нулевых строк, 5) аналогичные операции со столбцами.

Две матрицы будем называть эквивалентными, если они могут быть получены одна из другой элементарными преобразованиями. Справедлива следующая теорема.

Элементарные преобразования не меняют ранга матрицы. Для нахождения ранга матрицы ее приводят с помощью элементарных преобразований к ступенчатому виду, тогда ранг исходной матрицы равен рангу эквивалентной ей ступенчатой матрицы. При этом рекомендуется приводить элементарные преобразования исключительно со строками, в особенности, если это касается решения систем линейных уравнений