Geum.ru

«Численные методы»

Вид материалаРеферат
Подобный материал:



РОСЖЕЛДОР

Государственное образовательное учреждение высшего профессионального образования

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (СГУПС)


Кафедра «Информационные технологии транспорта»


Реферат


§по дисциплине «Численные методы»





Краткая рецензия:

_____________________________________________________________________________

_____________________________________________________________________________

_____________________________________________________________________________


________________________________

(запись о допуске к защите)


________________________________

(оценка по результатам защиты)


___________ Э.А. Усова

(подпись)


__________________

(дата защиты)


Новосибирск

2010



План:
  1. Введение.
  2. Теория.
  3. Системные требования.
  4. Код программы.



Введение.


Данная работа выполнялась с применением всех моих знаний полученных в ходе прослушивания курса предмета – “Численные методы”. Данная программа была разработана в среде Delphi. Программа предназначена для решения систем линейных уравнений методом Гаусса.


Теория.

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.


Пусть исходная система выглядит следующим образом:





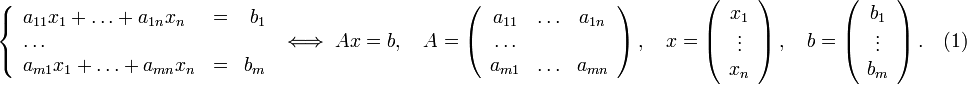
Матрица A называется основной матрицей системы, b — столбцом свободных членов.


Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):





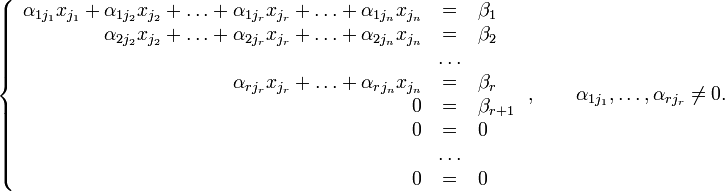
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных [3].


Тогда переменные называются главными переменными. Все остальные называются свободными.


Если хотя бы одно число , где i > r, то рассматриваемая система несовместна.


Пусть, что для любых i > r.


Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где — номер строки):





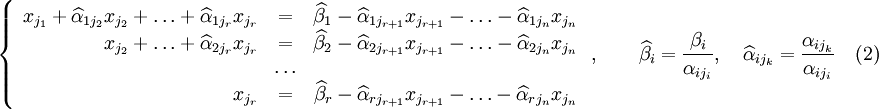
где


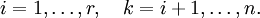
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.


Условие совместности


Упомянутое выше условие для всех может быть сформулировано в качестве необходимого и достаточного условия совместности:


Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).


Алгоритм

[править]

Описание


Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получавшуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.


Метод Гаусса требует порядка O(n3) действий.


Этот метод опирается на:


Простейший случай


В простейшем случае алгоритм выглядит так:





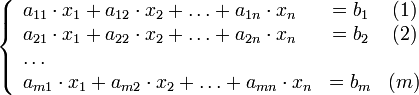
Прямой ход:




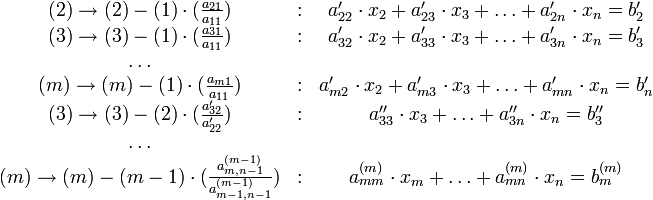
Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.


Пример


Покажем, как методом Гаусса можно решить следующую систему




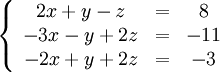
Обнулим коэффициенты при X во второй и третьей строчках. Для этого домножим их на 2\3 и 1 соответственно и сложим с первой строкой:




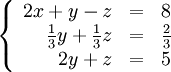
Теперь обнулим коэффициент при Y в третьей строке, домножив вторую строку на 6 и вычитая из неё третью:



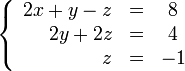
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.


На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

Z= -1 из третьего;

Y= 3 из второго, подставив полученное

X = 2 из первого, подставив полученные и .


Таким образом исходная система решена.


В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.


Системные требования:

ОС: Windows 95 и выше.

Процессор: Pentium 120Мгц и выше.

ОЗУ: 16мб и выше.

Место на HDD: 20мб.


Код программы:


uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, Grids, StdCtrls;


const MaxDimension = 10;


type


Vector = array[1..MaxDimension] of Double;

Matrix = array[1..MaxDimension] of Vector;


TForm3 = class(TForm)

Edit1: TEdit;

StringGrid1: TStringGrid;

StringGrid2: TStringGrid;

Button1: TButton;

Label2: TLabel;

Label3: TLabel;

ListBox1: TListBox;

Label4: TLabel;

Label1: TLabel;

Label5: TLabel;

Button2: TButton;

procedure Edit1Change(Sender: TObject);

procedure Button1Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure Button2Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;


var

Form3: TForm3;


implementation


{$R *.dfm}


procedure TForm3.Button1Click(Sender: TObject);

var a: Matrix;

b,x: Vector;

h: Double;

i,j,k,n:integer;

begin

//Ввод данных

//Размерность системы

n := StrToIntDef(Text, StringGrid1.ColCount);

//Коэффициенты

for j := 0 to n - 1 do

for i := 0 to n - 1 do

a[i + 1, j + 1] := StrToFloatDef(StringGrid1.Cells[j, i], 0);

//Правая часть уравнения

for I := 0 to n - 1 do b[i + 1] := StrToFloatDef(StringGrid2.Cells[0, i], 0);

//Прямой ход - исключение переменных

for i:=1 to n-1 do

for j:=i+1 to n do

begin

a[j,i]:=-a[j,i]/a[i,i];

for k:=i+1 to n do

a[j,k]:=a[j,k]+a[j,i]*a[i,k];

b[j]:=b[j]+a[j,i]*b[i]

end;

x[n]:=b[n]/a[n,n];

//Обратный ход - нахождение корней

for i:=n-1 downto 1 do

begin

h:=b[i];

for j:=i+1 to n do h:=h-x[j]*a[i,j];

x[i]:=h/a[i,i]

end;

//Вывод результата

for i:=1 to n do ListBox1.Items.Append('x(' + IntToStr(i) + ')=' + FloatToStr(x[i]));

end;

procedure TForm3.Edit1Change(Sender: TObject);

begin

with StringGrid1, Edit1 do

begin

ColCount := StrToIntDef(Text, 3);

RowCount := StrToIntDef(Text, 3);

end;

with StringGrid2, Edit1 do

RowCount := StrToIntDef(Text, 3)

end;


procedure TForm3.FormCreate(Sender: TObject);

var i, j: integer;

begin

//Заполнить коэф уравнения

Randomize;

for I := 0 to StrToIntDef(Text, StringGrid1.ColCount) - 1 do

for J := 0 to StrToIntDef(Text, StringGrid1.RowCount) - 1 do

StringGrid1.Cells[I, J] := IntToStr(Random(100));

for I := 0 to StrToIntDef(Text, StringGrid2.RowCount) - 1 do

StringGrid2.Cells[0, I] := IntToStr(Random(100))

end;


//кнопка выхода

procedure TForm3.Button2Click(Sender: TObject);

begin

close;

end;


end.