Geum.ru

Рабочая программа учебной дисциплины численные методы Направление подготовки 210400 Радиотехника

Вид материалаРабочая программа

Содержание


Радиотехнические средства приема, передачи и обработки сигналов
1. Цели и задачи учебной дисциплины
2. Место учебной дисциплины в структуре ООП.
3. Требования к результатам освоения дисциплины
4. Образовательные технологии
5. Структура учебной дисциплины (модуля)
5.1 Содержание учебной дисциплины. Объем дисциплины и виды учебных занятий
Самостоятельная работа (всего)
И(или) другие виды самостоятельной работы
5.2. Содержание разделов учебной дисциплины
5.3 Разделы учебной дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
5.4 Разделы дисциплин и виды занятий
6. Лабораторный практикум
9. Учебно-методическое и информационное обеспечение учебной дисциплины
10. Материально-техническое обеспечение дисциплины
Подобный материал:
Министерство образования и науки Российской Федерации

ГОУВПО «Мордовский государственный университет им. Н.П.Огарёва»

Институт физики и химии


Кафедра систем автоматизированного проектирования



«УТВЕРЖДАЮ»

_____________________

_____________________

«______»__________201_ г.



РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

Численные методы


Направление подготовки

210400 Радиотехника


Профиль подготовки

Радиотехнические средства приема, передачи и обработки сигналов


Квалификация (степень) выпускника

Бакалавр


Форма обучения

очная


г. Саранск

2011 г.

1. Цели и задачи учебной дисциплины:

Целью освоения курса «Численные методы» является знание основных численных методов, применяемых для решения задач физики и радиотехники.

В процессе изучения дисциплины решаются следующие задачи:

– овладение математической и алгоритмической составляющей численных методов, применяемых при решении научно-технических задач;

– формирование устойчивых навыков применения компьютерных технологий для реализации численных методов, научном анализе ситуаций, возникающих в ходе создания новой техники и новых технологий;

– умение отбирать наиболее эффективные численные методы решения конкретной задачи, учитывая такие факторы, как: алгоритмическую простоту метода, точность вычислений, быстроту сходимости, наличие дополнительных условий для применения метода, устойчивость метода;

– умение интерпретировать результаты расчетов, полученных численными методами.


2. Место учебной дисциплины в структуре ООП.

Дисциплина «Численные методы» относится к вариативной части естественно-научного цикла.

Перед изучением дисциплины у студента должны быть сформированы следующие компетенции:

– владеет культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения (ОК–1);

– умеет логически верно, аргументированно и ясно строить устную и письменную речь (ОК-2);

    – владеет основными методами, способами и средствами получения, хранения, переработки информации, имеет навыки работы с компьютером, как средством управления информацией (ОК-12);

    – способен работать с информацией в глобальных компьютерных сетях (ОК-13).

Необходимыми для изучения данной дисциплины являются знания математики и информатики в следующем объеме:

    – математика: дифференциальное и интегральное исчисление, аналитическая геометрия на плоскости, линейная алгебра, обыкновенные дифференциальные уравнения, уравнения математической физики;

    – информатика: алгоритмы, языки программирования, электронные таблицы;

    – физика: основные законы механики, термодинамики, электродинамики.

Помимо самостоятельного значения курс является предшествующей дисциплиной для многих общепрофессиональных дисциплин, использующих компьютерные технологии и численные методы для решения профессиональных задач.


3. Требования к результатам освоения дисциплины

Процесс изучения дисциплины направлен на формирование следующих компетенций:

– использует основные законы естественнонаучных дисциплин в профессиональной деятельности, применяет методы математического анализа и моделирования, теоретического и экспериментального исследования (ОК-10);

– представляет адекватную современному уровню знаний научную картину мира на основе знания основных положений, законов и методов естественных наук и математики (ПК-1);

– способен выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, привлекать для их решения соответствующий физико-математический аппарат (ПК-2);

– владеет основными приемами обработки и представления экспериментальных данных (ПК-5).

В результате изучения дисциплины студент должен:

    Знать: математическую основу наиболее распространенных численных методов решения физических задач;

    Уметь:

– приводить анализ типовых математических моделей физических процессов или явлений;

– разрабатывать алгоритмы базовых численных методов и выбирать наиболее рациональную форму представления исходных данных и полученных результатов;

    Владеть: современными методами реализации построенной модели с применением электронных таблиц или языка программирования высокого уровня.



4. Образовательные технологии

    Изучение дисциплины предполагает использование традиционных способов коллективного обучения – лекций, лабораторных занятий, индивидуальных заданий с последующей отчетностью. Применяемые информационные технологии: лекции в форме презентаций, обучающие и тестирующие программы, электронные учебники

5. Структура учебной дисциплины (модуля)



№ п/п
Раздел учебной дисциплины
Курс
Семестр
Неделя семестра
Виды учебной работы, в т.ч. СРС и трудоёмкость (в часах)
Формы текущего

контроля

успеваемости

(по неделям семестра)
Форма

промежуточной

аттестации

лекции
Лабораторные занятия
СРС

1.
Решение нелинейных уравнений
2
4
1
1
2
4
Отчет по лр№1



2.
Вычисление определенных интегралов
2
4
2
1
2
4
Отчет по лр№2



3.
Решение систем линейных уравнений
2
4
3-4
2
4
8
Отчет по лр№3-4



4.
Вычисление обратных матриц и определителей
2
4
5
1
2
4
Отчет по лр№5



5.
Решение систем нелинейных уравнений
2
4
6
1
2
4
Отчет по лр№6



6.
Интерполяция функций
2
4
7-8
2
4
4
Отчет по лр№7-8



7.
Аппроксимация функций
2
4
9-10
2
4
8
Отчет по лр№9-10



8.
Решение обыкновенных дифференциальных уравнений
2
4
11-13
2
8
6
Отчет по лр№11-13



9.
Решение дифференциальных уравнений в частных производных
2
4
14
2



4
Отчет по теме лекции



10.
Оптимизация функций
2
4
15-18
4
8
8
Отчет по лр№14-17
Зачет



5.1 Содержание учебной дисциплины. Объем дисциплины и виды учебных занятий

Вид учебной работы
Всего

часов
Семестры

4

Аудиторные занятия (всего)
54
54

В том числе:






Лекции
18
18

Практические занятия (ПЗ)






Семинары (С)






Лабораторные работы (ЛР)
36
36

Самостоятельная работа (всего)
54
54

В том числе:






Курсовая работа






Расчетно-графические работы






Реферат






И(или) другие виды самостоятельной работы:
54
54

Подготовка к лабораторным работам
46
46

Подготовка к зачету
8
8

Вид текущего контроля успеваемости






Вид промежуточной аттестации




зач.

Общая трудоемкость дисциплины Час.

Зач. ед.
108

3
108

3


5.2. Содержание разделов учебной дисциплины

№ п/п
Наименование раздела дисциплины
Содержание раздела
Формы текущего контроля успеваемости
(по неделям семестра)

1
2
3
4

1.
Решение нелинейных уравнений
Метод половинного деления. Метод Ньютона. Метод хорд.
ИДЗ №1
Отчет по ЛР№1
(1 неделя)

2.
Вычисление определенных интегралов
Метод прямоугольников. Метод трапеций. Метод Симпсона
ИДЗ №2

Отчет по ЛР№2
(2 неделя)

3
Решение систем линейных уравнений
Прямые методы: метод Гаусса. Итерационные методы: метод простой итерации, метод Зейделя; условия сходимости.
ИДЗ №3-5

Отчет по ЛР№3-5 (3-5 недели)

4
Вычисление обратных матриц и определителей
Метод Гаусса вычисления обратной матрицы и определителя
ИДЗ №6

Отчет по ЛР№6
(6 неделя)

5
Решение систем нелинейных уравнений
Метод Ньютона решения систем нелинейных уравнений
ИДЗ №7

Отчет по ЛР№7
(7 неделя)

6.
Интерполяция функций
Полином Лагранжа. Схема Эйткена
ИДЗ №8

Отчет по ЛР№8
(8 неделя)

7.
Аппроксимация функций
Метод наименьших квадратов
ИДЗ №9

Отчет по ЛР№9
(9 неделя)

8.
Решение обыкновенных дифференциальных уравнений
Метод Эйлера, модифицированный метод Эйлера, метод Эйлера с итерациями, метод Рунге-Кутта
ИДЗ №10-13

Отчет по ЛР№10-13 (10-13 недели)

1
2
3
4

9.
Решение дифференциальных уравнений в частных производных
Замена производных конечными разностями. Стационарные уравнения. Нестационарные уравнения: уравнение теплопроводности.
Отчет по теме лекции (14 недели)

10
Оптимизация функций
Оптимизация без ограничений: метод Нелдера-Мида. Оптимизация с ограничениями: метод множителей Лагранжа, комплексный метод. Задачи линейного программирования. Задачи многокритериальной оптимизации
ИДЗ №14-17

Отчет по ЛР№14-17
(15-18 недели)


5.3 Разделы учебной дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами

№ п/п
Наименование обеспечиваемых (последующих) дисциплин
№ № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин

1
2
3
4
5
6
7
8
9
10

1
Основы схемотехнического моделирования
+



+
+
+



+



+



2
Метрология и радиоизмерения
+
+
+



+
+
+



+



3
Радиотехнические цепи и сигналы



+
+



+
+
+
+



+

4
Основы компьютерного проектирования РЭС
+



+
+
+



+






+

5
Схемотехника аналоговых электронных устройств



+
+



+



+



+



6
Цифровые устройства и микропроцессоры
+



+
+
+



+
+



+

7
Цифровая обработка сигналов
+
+
+



+
+
+










5.4 Разделы дисциплин и виды занятий

№ п/п
Наименование раздела дисциплины
Лекц.
Практ.

зан.
Лаб.

зан.
Семин.
СРС
Всего

час.

1.
Решение нелинейных уравнений
1



2



4
7

2.
Вычисление определенных интегралов
1



2



4
7

3.
Решение систем линейных уравнений
2



4



8
14

4.
Вычисление обратных матриц и определителей
1



2



4
7

5.
Решение систем нелинейных уравнений
1



2



4
7

6
Интерполяция функций
2



4



4
10

7
Аппроксимация функций
2



4



8
14

8
Решение обыкновенных дифференциальных уравнений
2



8



6
16

9
Решение дифференциальных уравнений в частных производных
2









4
6

10
Оптимизация функций
4



8



8
20

6. Лабораторный практикум


№ п/п
№ раздела дисциплины
Наименования лабораторных работ
Трудо­емкость (час.)

1
1
Метод половинного деления. Метод Ньютона. Метод хорд.
2

2
2
Метод прямоугольников. Метод трапеций. Метод Симпсона
2

3
3
Решение систем линейных уравнений: прямые методы- метод Гаусса. Итерационные методы: метод простой итерации, метод Зейделя; условия сходимости.
4

4
4
Метод Гаусса вычисления обратной матрицы и определителя
2

5
5
Метод Ньютона решения систем нелинейных уравнений
2

6
6
Полином Лагранжа. Схема Эйткена
4

7
7
Метод наименьших квадратов
4

8
8
Метод Эйлера, модифицированный метод Эйлера, метод Эйлера с итерациями, метод Рунге-Кутта
8

9
10
Оптимизация без ограничений: метод Нелдера-Мида Задачи линейного программирования.
8


8. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов

Формой текущего контроля знаний студентов является контроль правильности выполнения и оформления лабораторных и самостоятельных работ.

Формой промежуточного контроля знаний студентов является зачет.

Перечень индивидуальных заданий для проведения текущего контроля представлен в Приложении 1.


9. Учебно-методическое и информационное обеспечение учебной дисциплины:

а) основная литература
  1. Дьяконов В.П. Справочник по алгоритмам и программам для ПВМ -М.: Наука, 1987.
  2. Воробьев Г.Н.,Дашкова А.Н. Практикум по вычислительной математике. –М.:Высш.шк.1990-208 с.
  3. Шуп Т.Е. Прикладные численные методы в физике и технике. - М. Высш. шк.1990, 255 с.
  4. Банди Б. Методы оптимизации. М: Радио и связь, 1988-188 с.
  5. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах.- М.:Высшая школа, 2005, 544 с.

б) дополнительная литература
  1. Баутин Н.Н. Леонтович Е.А. Методы и приемы исследования динамических систем на плоскости –М: Наука,1989,438 с.,
  2. Шуп Т.Е.Решение инженерных задач на ЭВМ. - М.: Мир.1989, 238 с.
  3. Пономарев К.К. Составление и решение дифференциальных уравнений инженерно-технических задач. –М.: Наука, 1962, 267 с.
  4. Васильев А.Н. Научные вычисления в MICROSOFT EXCEL.- М.:Вильямс,2004, 512 с.

в) программное обеспечение и Интернет- ресурсы

Пакеты прикладных программ
  1. Microsoft Office (2003-2007) – (комплекс программ обработки текстовой, числовой и графической информации, обеспечивающий разностороннюю работу с наборами различных данных).


10. Материально-техническое обеспечение дисциплины:
  1. Аудитория для проведения лекционных занятий, имеющая необходимое количество посадочных мест (для занятий с группой из 30 студентов) и оснащенная оборудованием для проведения презентаций (ноутбук, проектор);
  2. Аудитория с персональными компьютерами для проведения лабораторных занятий, имеющая необходимое количество рабочих мест (для занятий с подгруппой из 12-15 студентов), оборудованная персональными компьютерами на базе процессора Intel Pentium II или выше, оснащенных необходимым системным и прикладным программным обеспечением.



Авторы (разработчики):

кафедра САПР



Доцент



Рябухина Е.А.

Программа одобрена на заседании

(Наименование уполномоченного органа вуза (УМК, НМС, Ученый совет)
от года, протокол № .

Приложение 1

Задания к методу Гаусса, методу Зейделя и методу простой итерации (варианты)


Вариант 1 Вариант 2




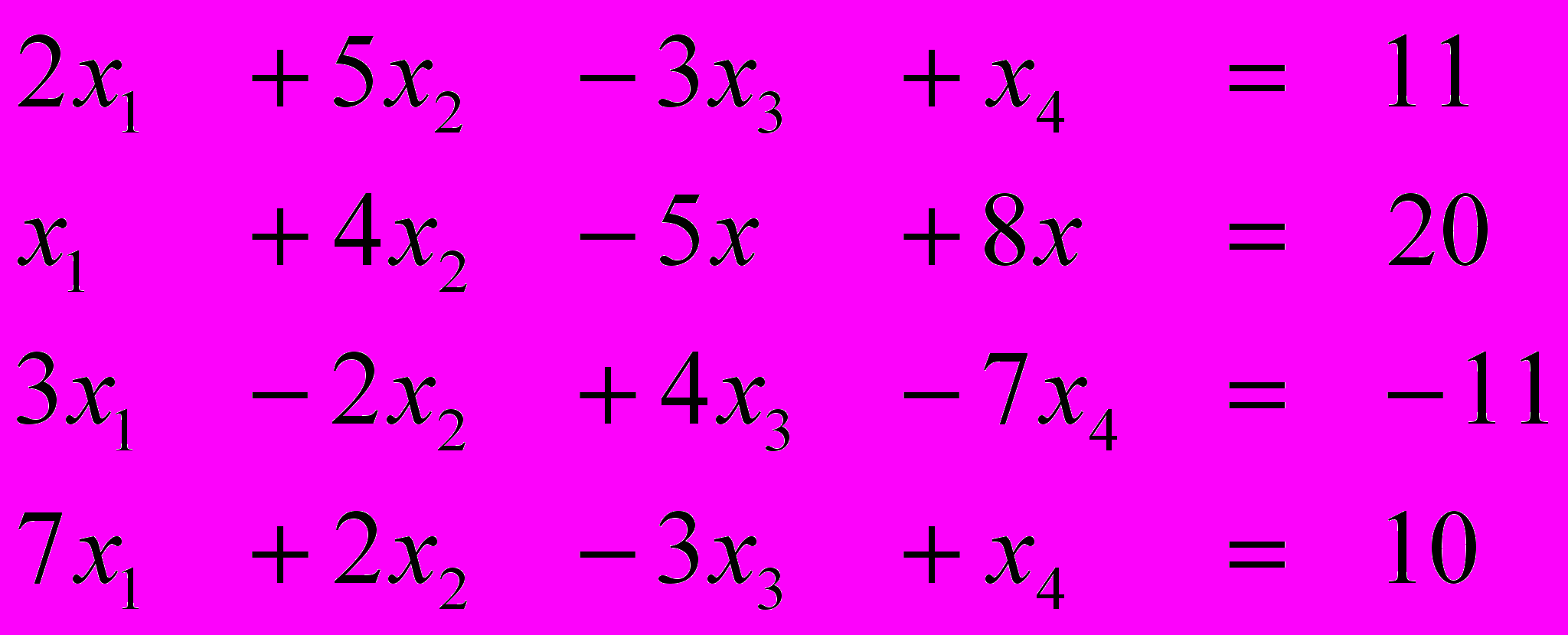
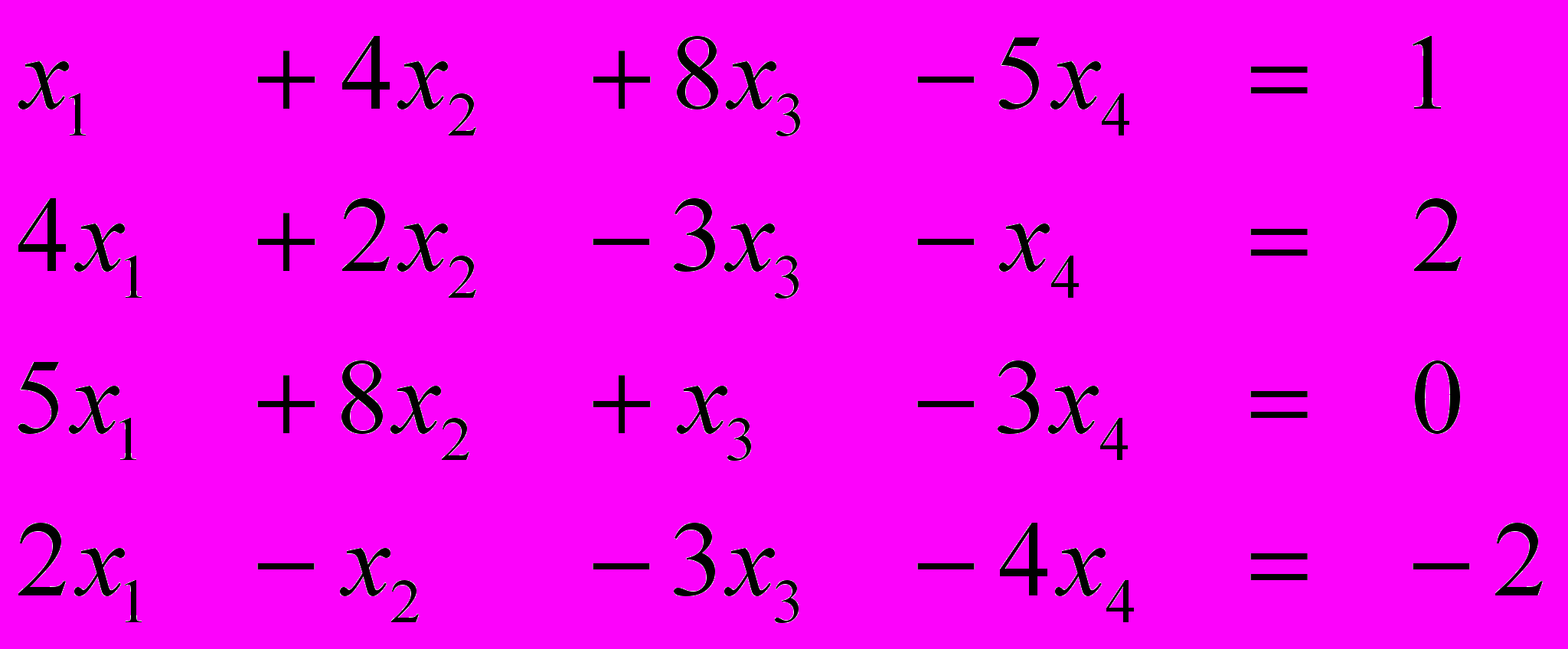
Ответ (1; 2; 1; 2) Ответ (2; -1; 1; 1)


Вариант 3 Вариант 4




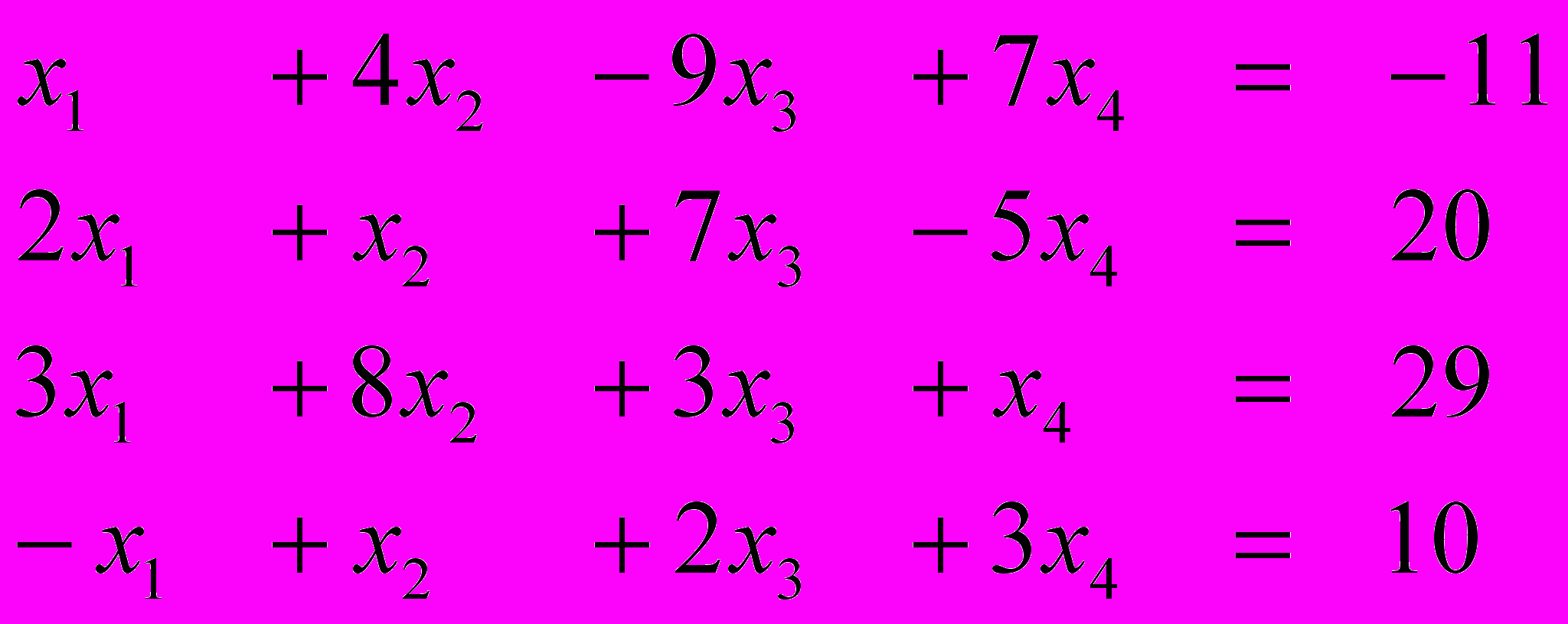
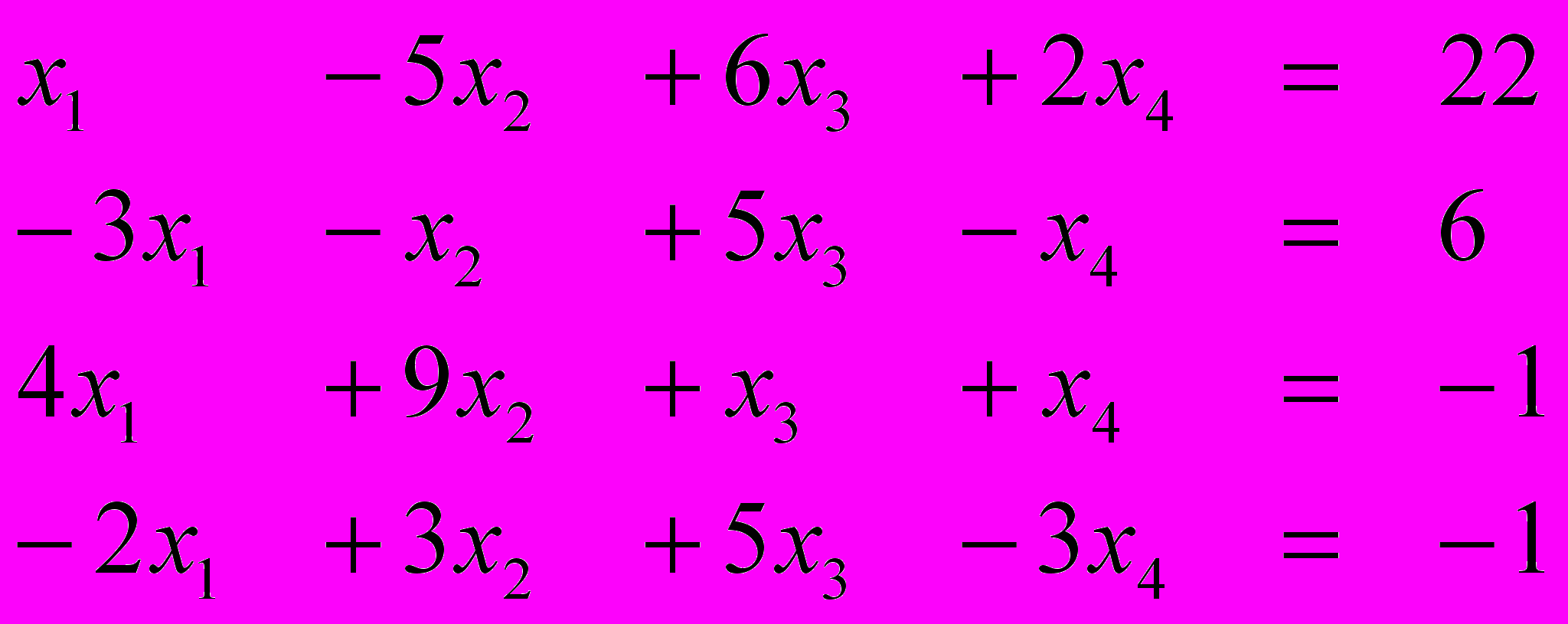
Ответ (1; 2; 3; 1) Ответ (1; -1; 2; 2)


Вариант 5 Вариант 6




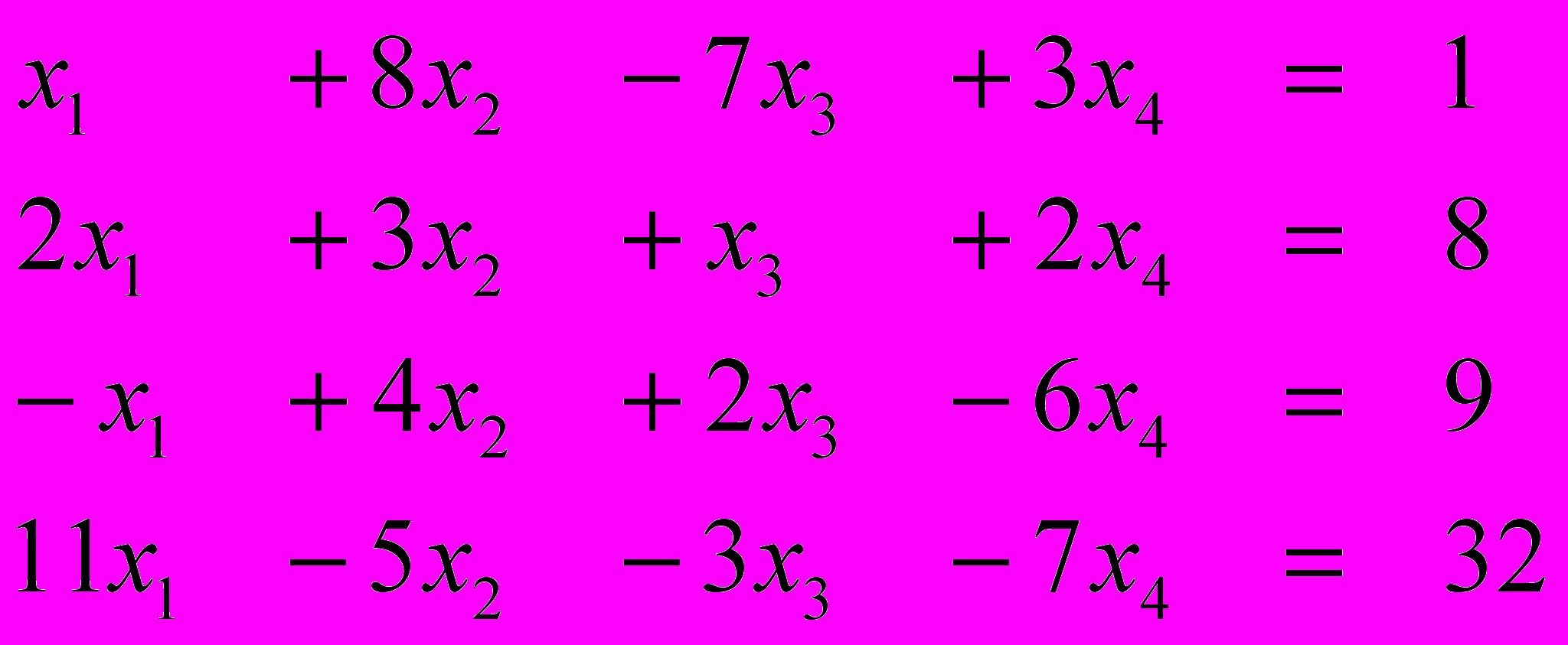
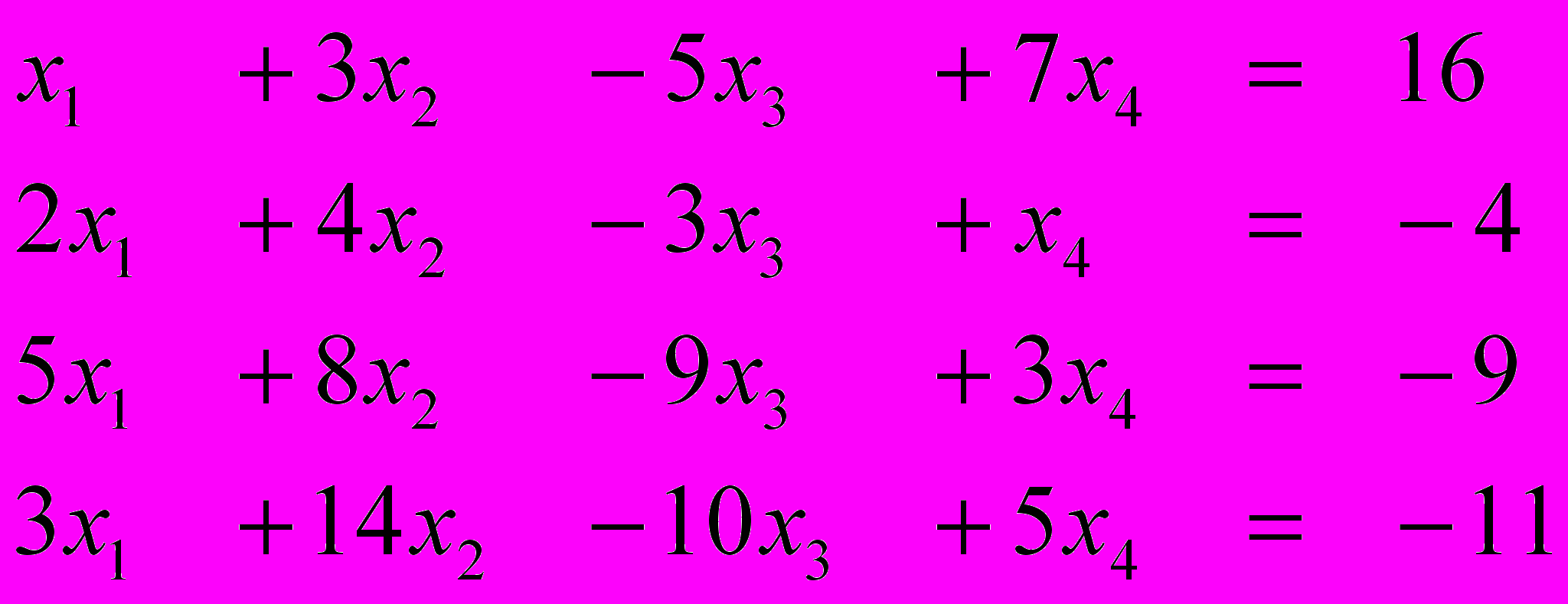
Ответ (3; 1; 1; -1) Ответ (1; -1; 2; 4)


Вариант 7 Вариант 8




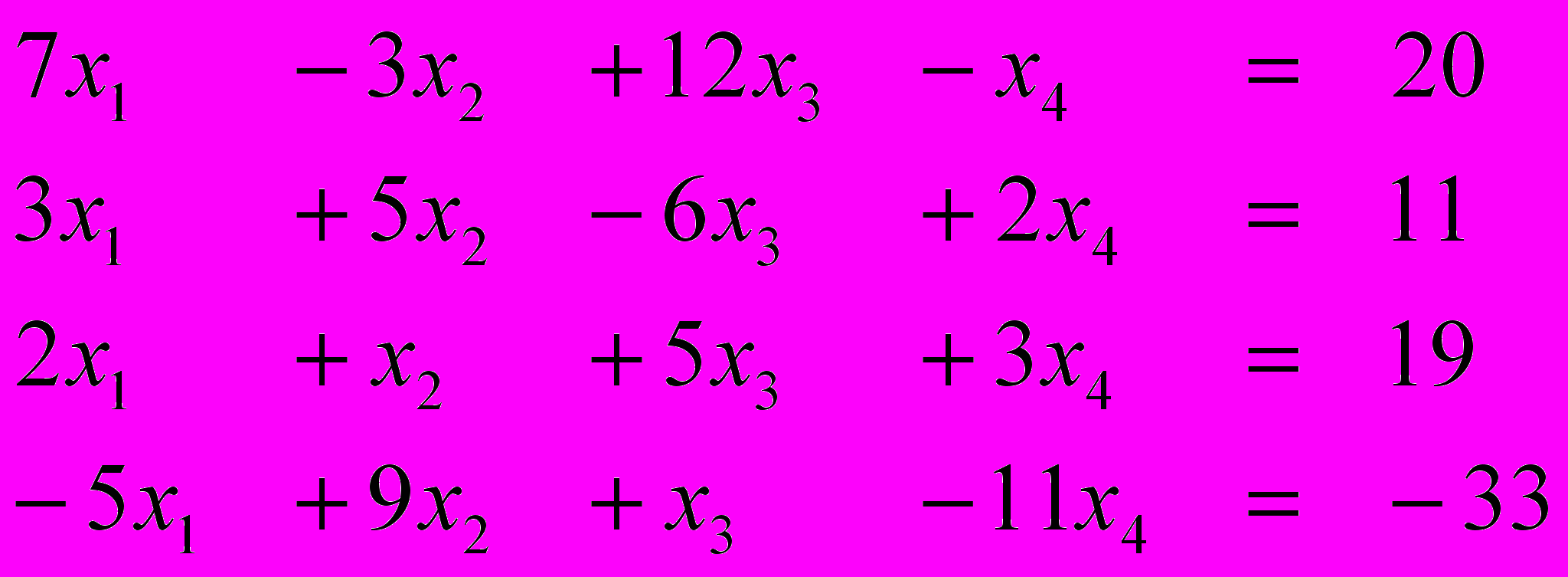
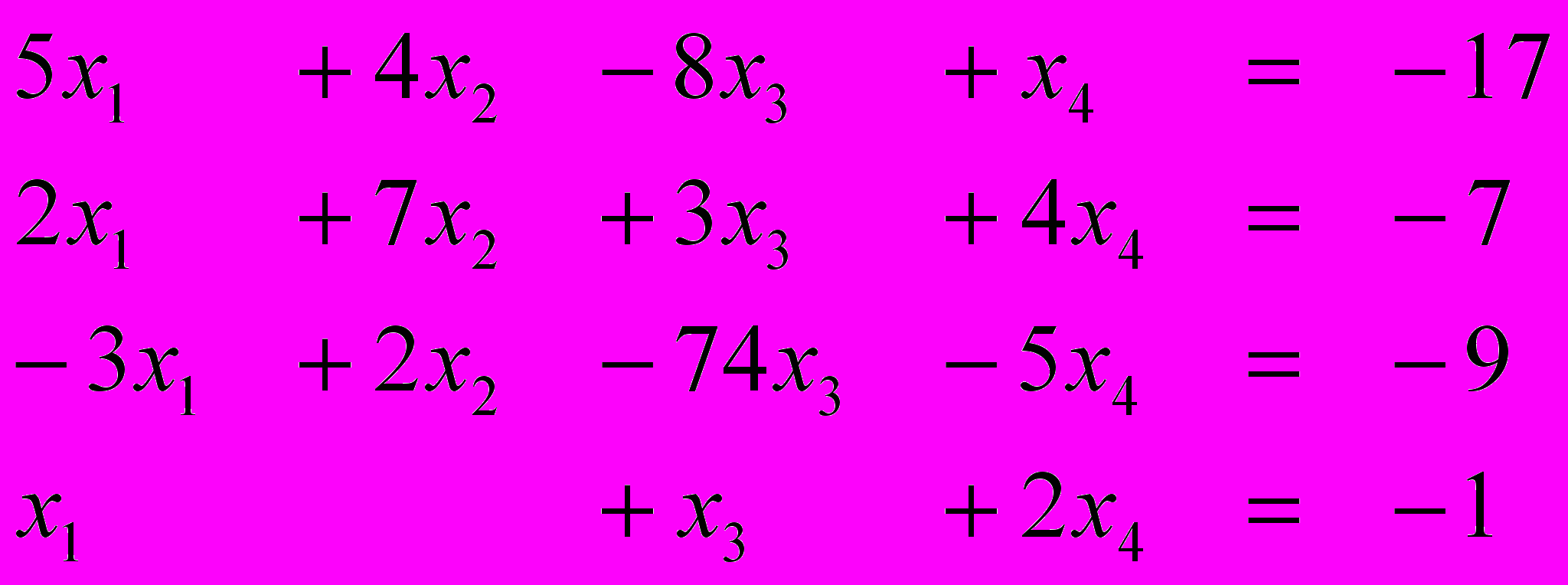
Ответ (2; 1; 1; 3) Ответ (1; -1; 2; -2)


Вариант 9 Вариант 10



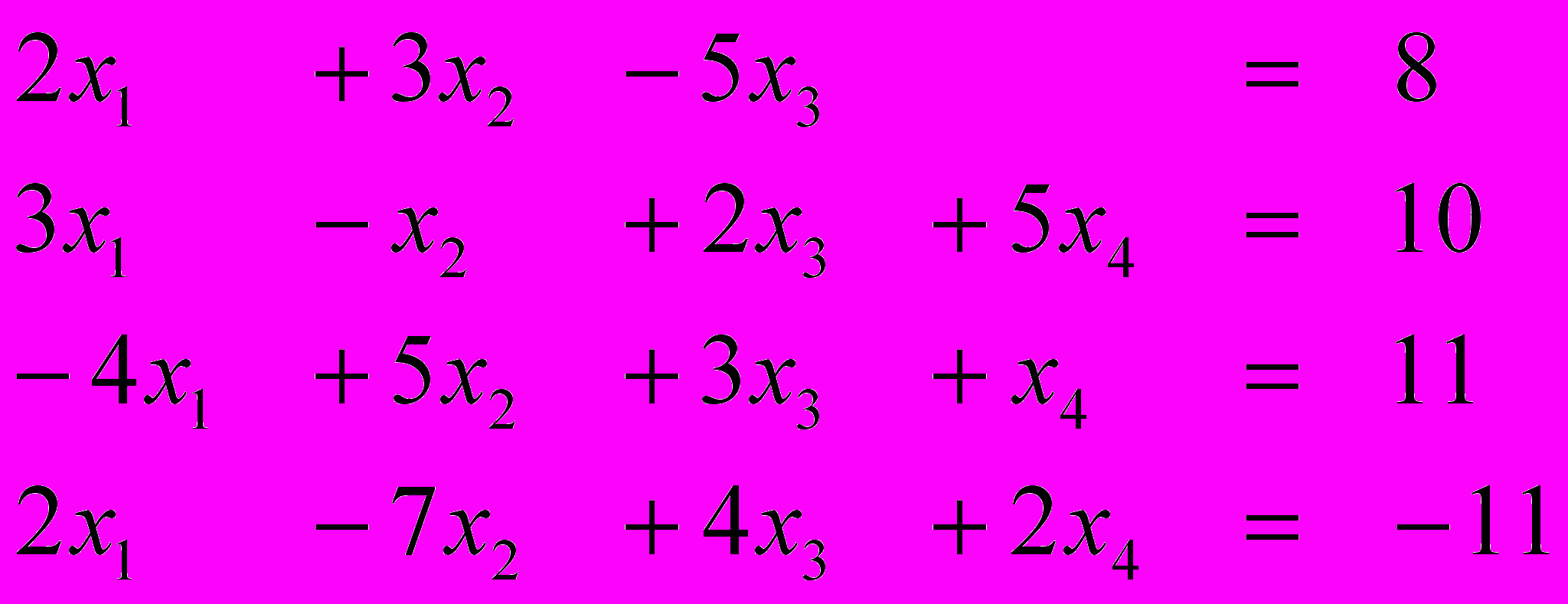
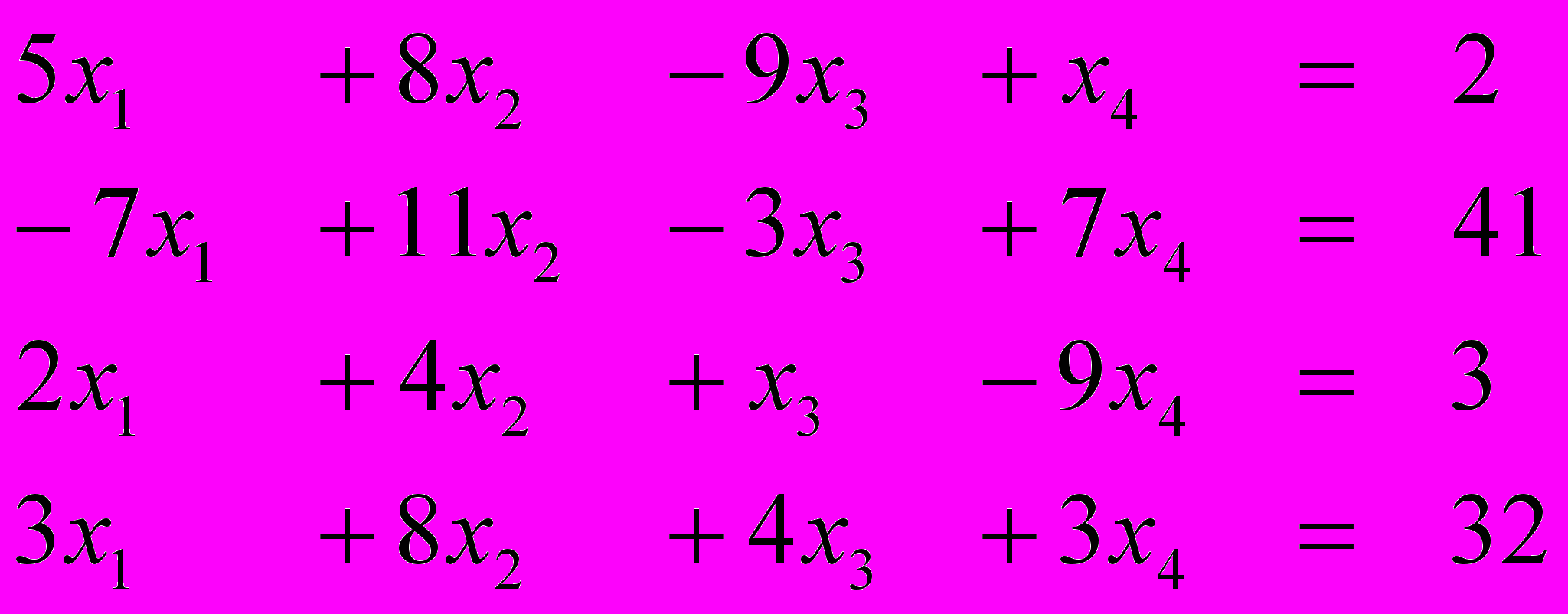
Ответ (2; 3; 1; 1) Ответ (-1; 3; 2; 1)

Вариант 11 Вариант 12




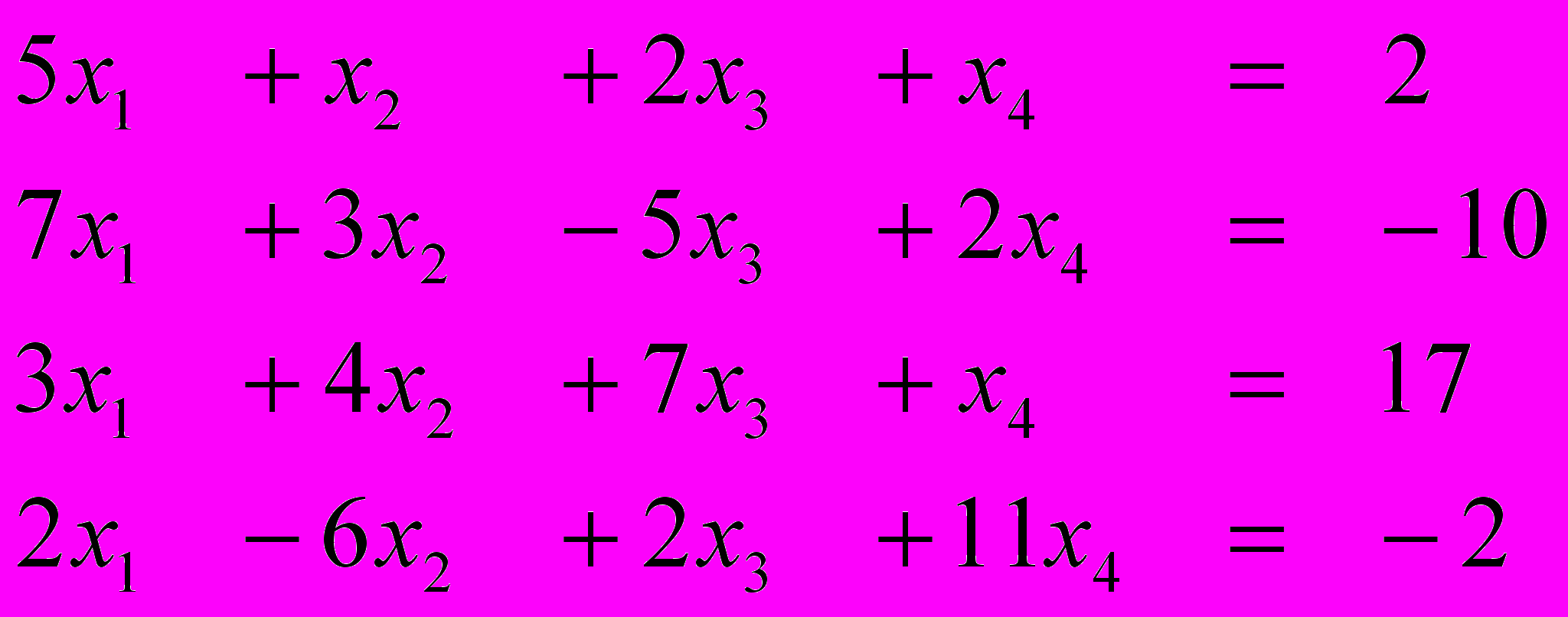
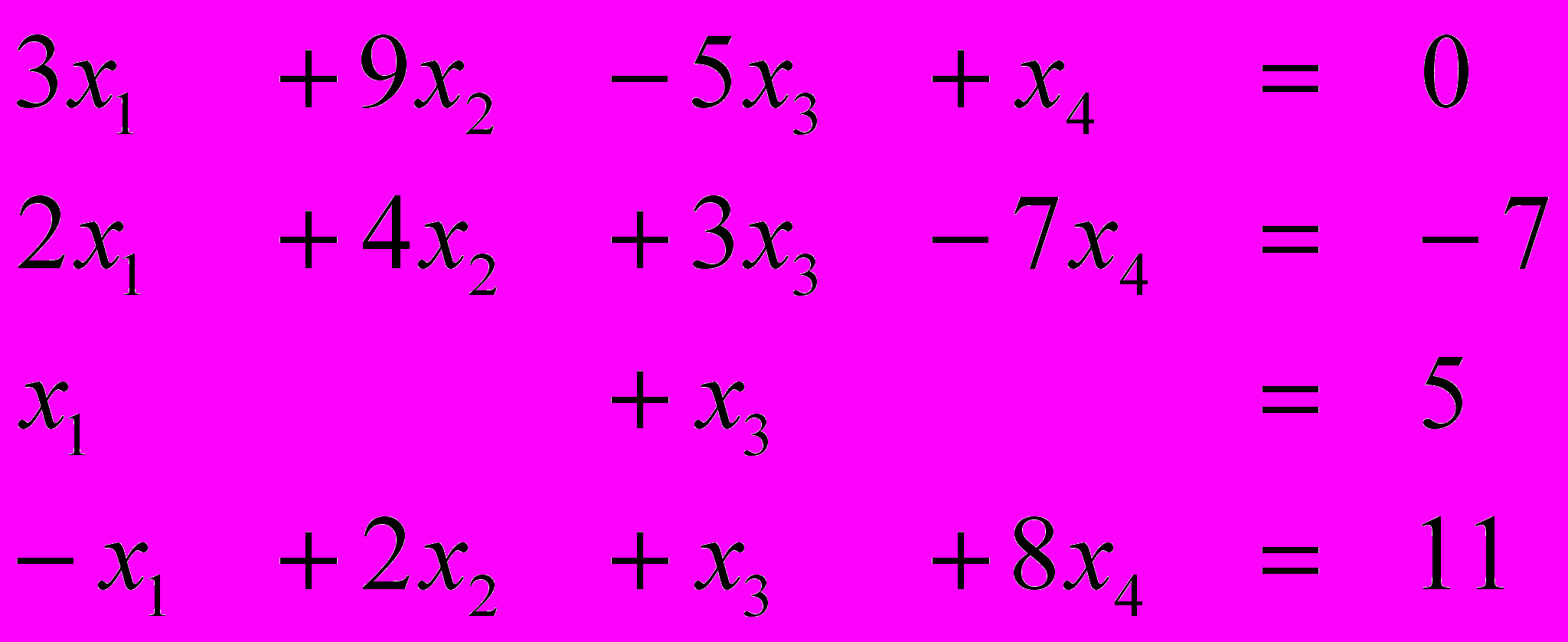
Ответ (-1; 1; 2; 2) Ответ (4; -1; 1; 2)


Вариант 13 Вариант 14




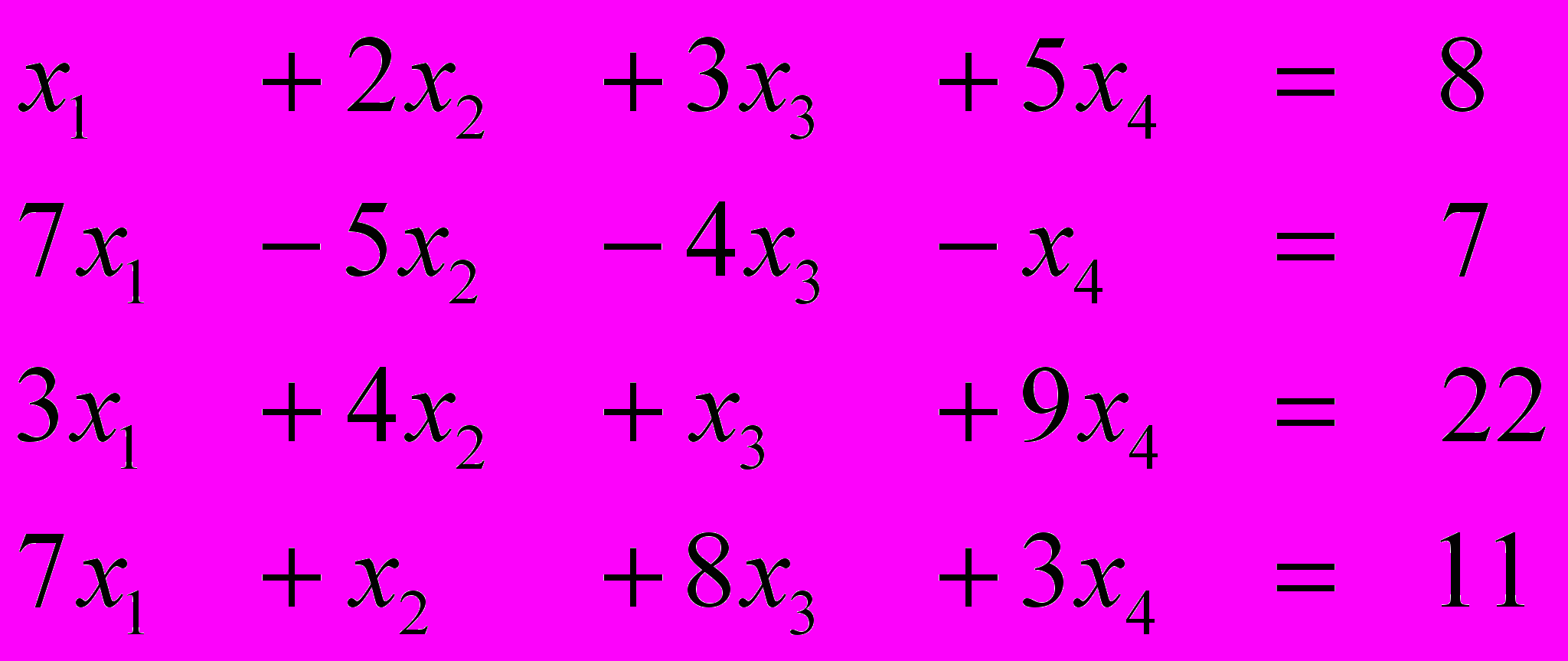
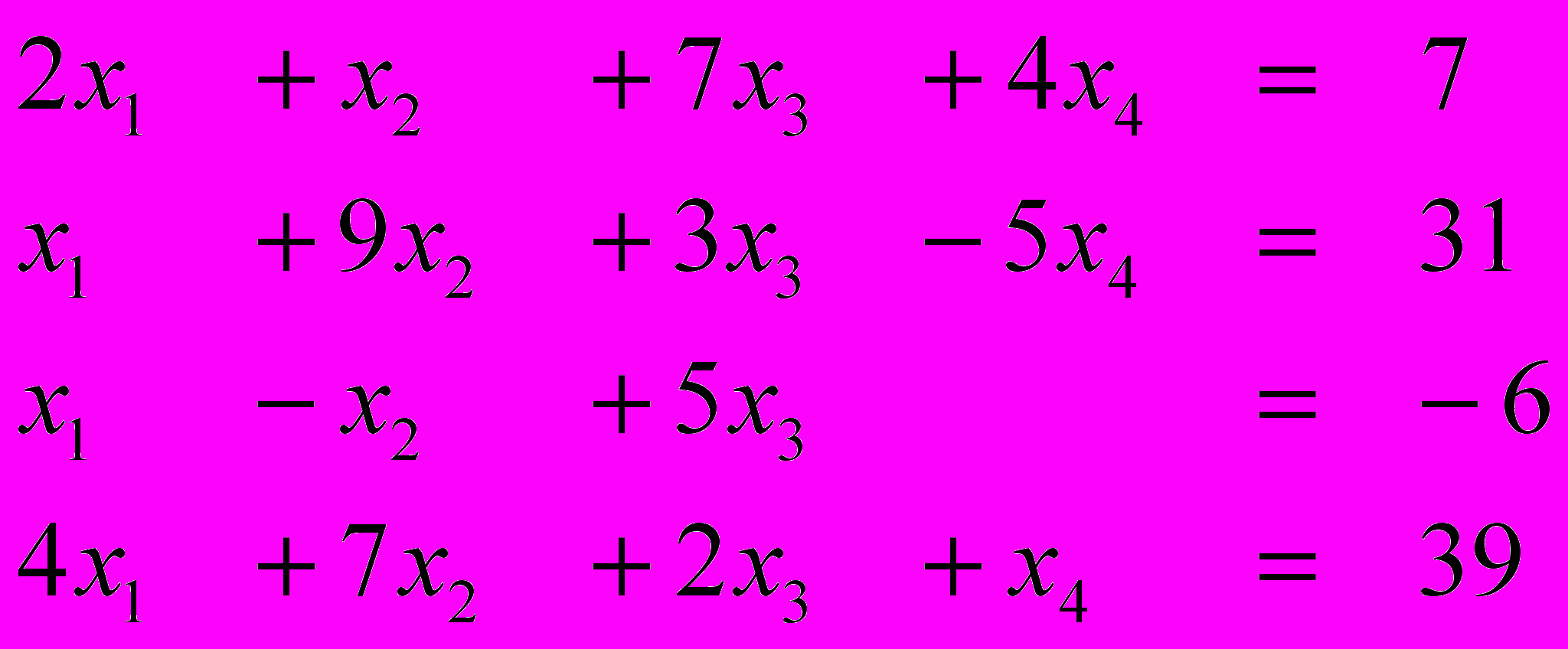
Ответ (2; 2; -1; 1) Ответ (3; 4; -1; 1)


Вариант 15 Вариант 16




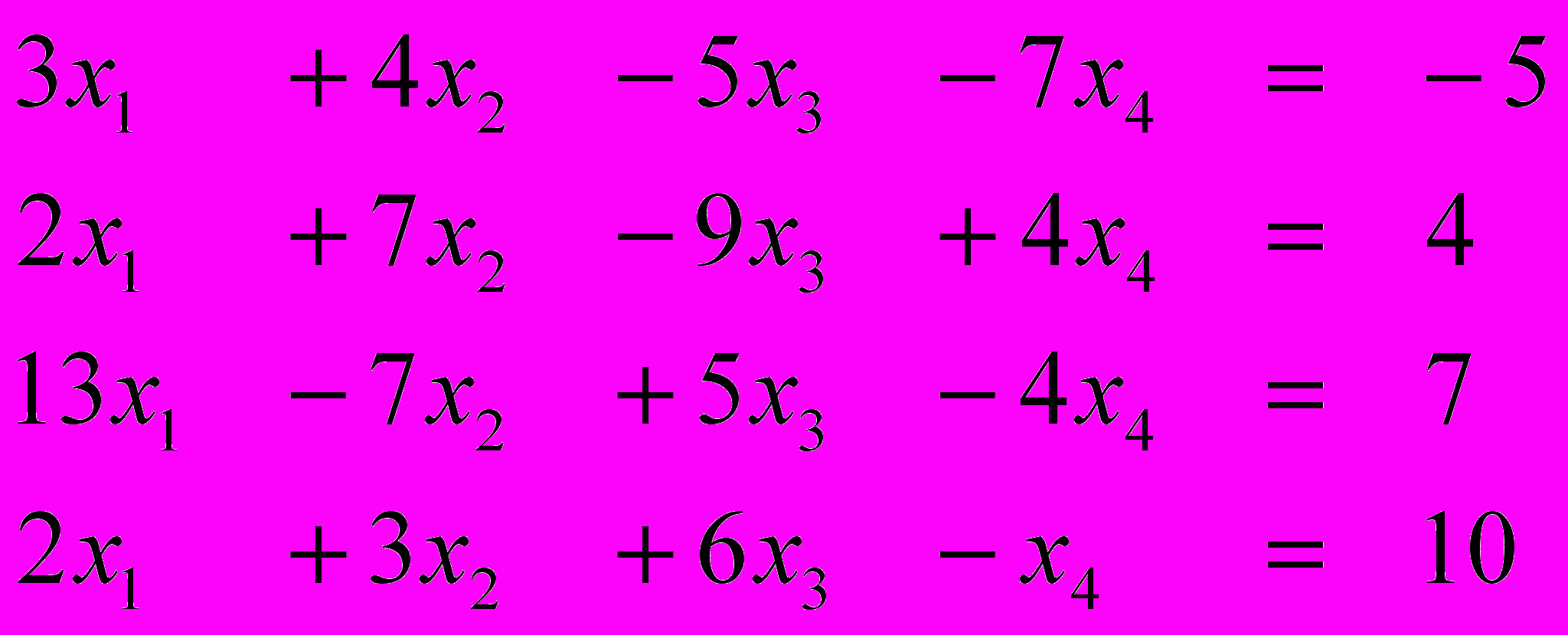
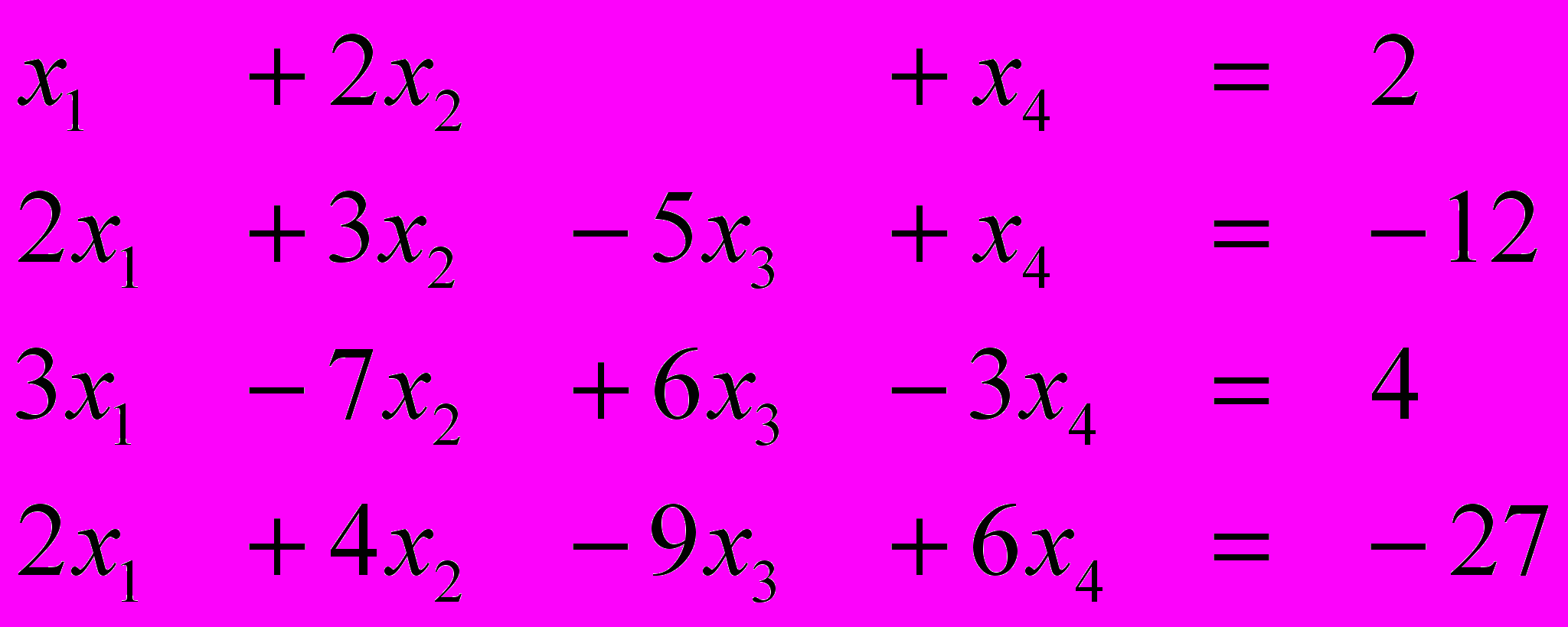
Ответ (1; 1; 1; 1) Ответ (-1; 2; 3; -1)


Задание к схеме Эйткена и полиному Лагранжа

x
y
№ варианта
x*
x
y
№ варианта
x*

0,2050
0,207921
1
0,2064
0,8902
1,23510
2
0,8942

0,2052
0,208130
5
0,2073
0,8909
1,23687
6
0,8973

0,2060
0,208964
9
0,2082
0,8919
1,23941
10
0,8958

0,2065
0,209486
13
0,2079
0,8940
1,24475
14
0,8948

0,2069
0,209904
17
0,2088
0,8944
1,24577
18
0,8934

0,2075
0,210530






0,8955
1,24858






0,2085
0,211575






0,8965
1,25114






0,2090
0,212097






0,8975
1,25371






0,2096
0,212724






0,9010
1,26275






0,2100
0,213142






0,9026
1,26691






x
y
№ варианта
x*
x
y
№ варианта
x*

0,6100
1,83781
3
0,6120
0,5400
1,66825
4
0,5415

0,6104
1,83686
7
0,6124
0,5405
1,66636
8
0,5424

0,6118
1,83354
11
0,6142
0,5410
1,66448
12
0,5436

0,6139
1,82860
15
0,6163
0,5420
1,66071
16
0,5442

0,6145
1,82720
19
0,6182
0,5429
1,65734
20
0,5451

0,6158
1,82416






0,5440
1,65322






0,6167
1,82207






0,5449
1,64987






0,6185
1,81791






0,5455
1,64764






0,6200
1,81446






0,5465
1,64393






0,6225
1,80876






0,5473
1,64097








Задания к методу Эйлера и методу Рунге-Кутта

№ варианта
Уравнение
Начальное приближение y0

Отрезок интегрирования

1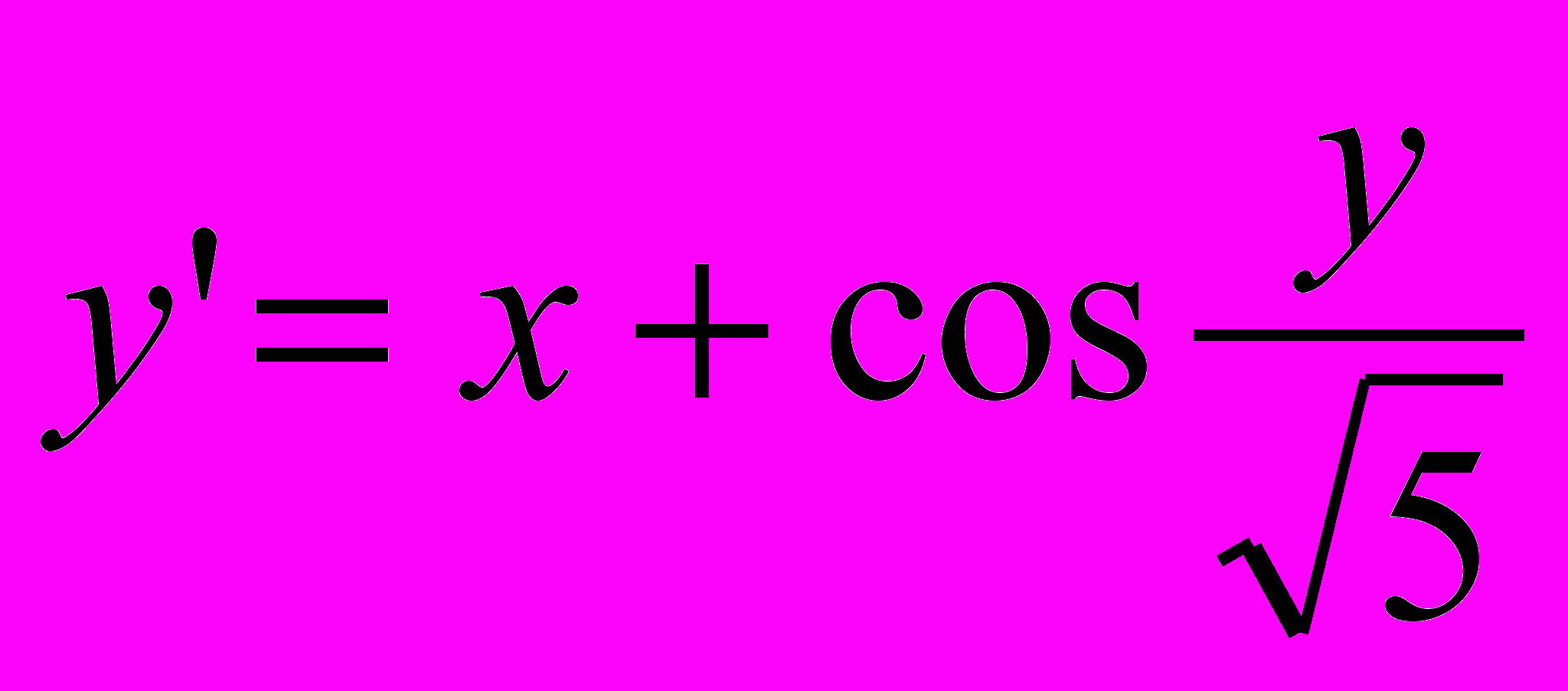


y0(1,8)=2,6
[1,8;2,8]

2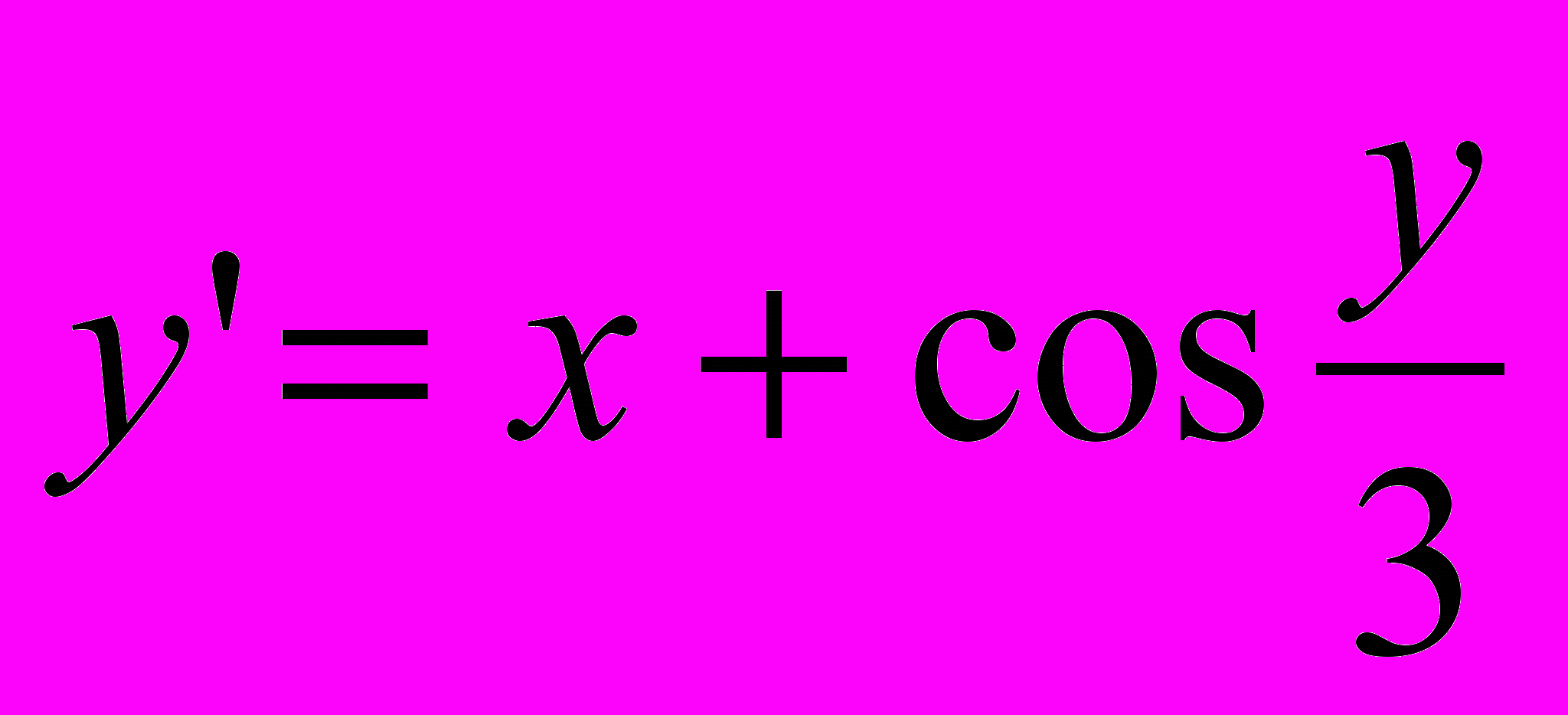


y0(1,6)=4,6
[1,6;2,6]

3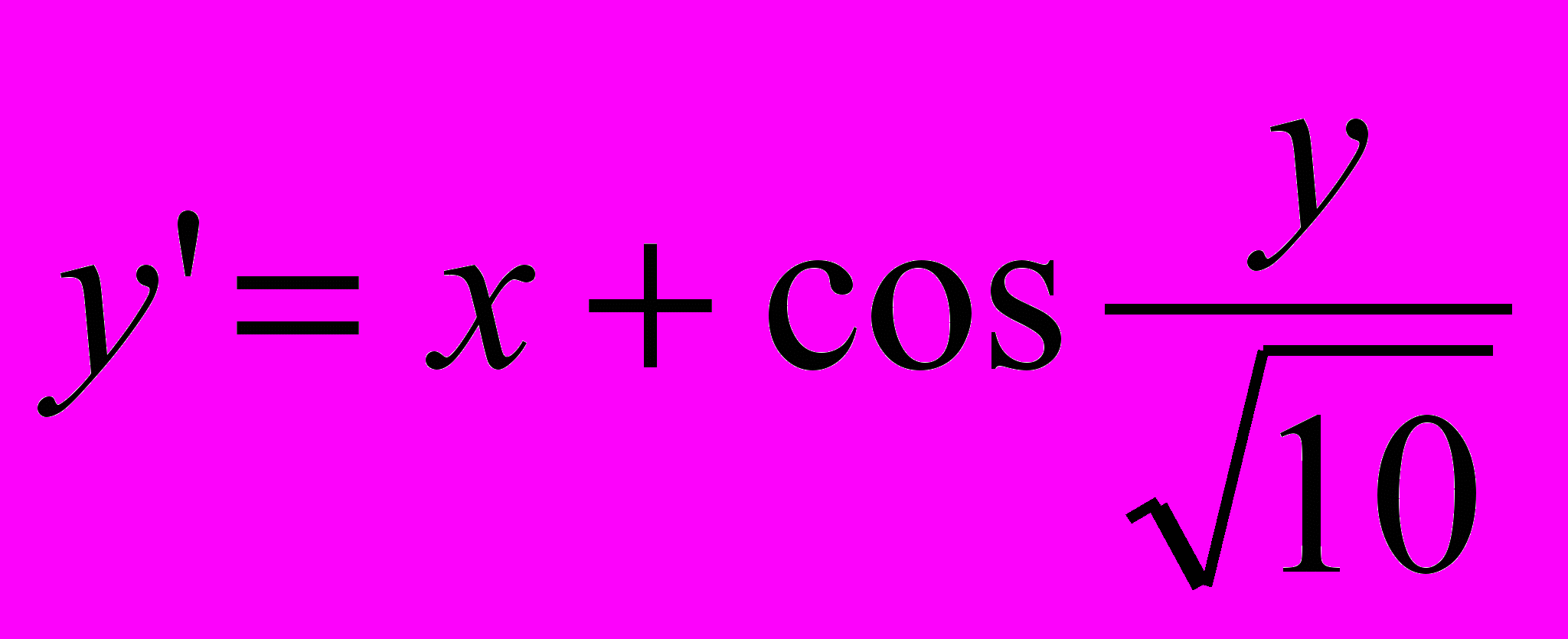


y0(0,6)=0,8
[0,6;1,6]

4


y0(0,5)=0,6
[0,5;1,5]

5


y0(1,7)=5,3
[1,7;2,7]

6


y0(1,4)=2,2
[1,4;2,4]

7


y0(1,4)=2,5
[1,4;2,4]

8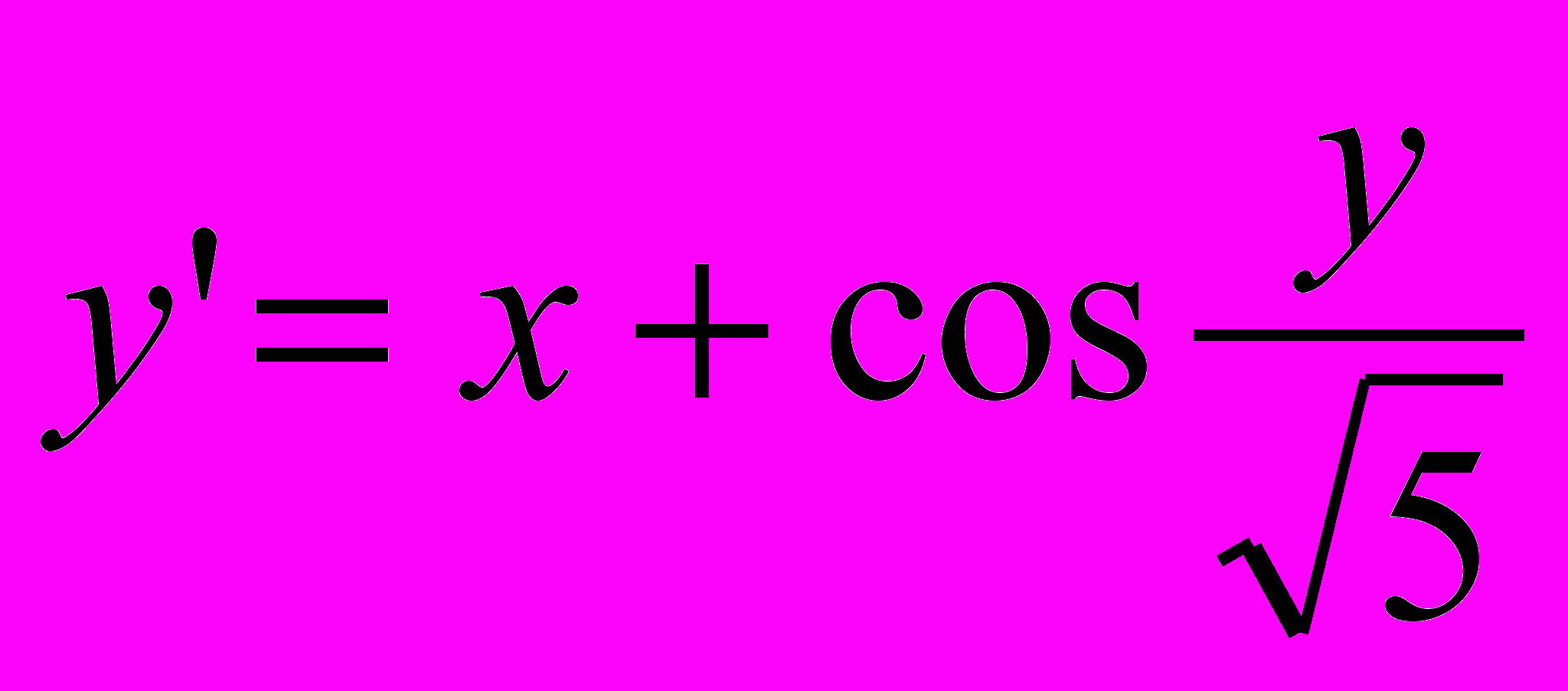


y0(0,8)=1,4
[0,8;2,8]

9


y0(1,2)=2,1
[1,2;2,2]

10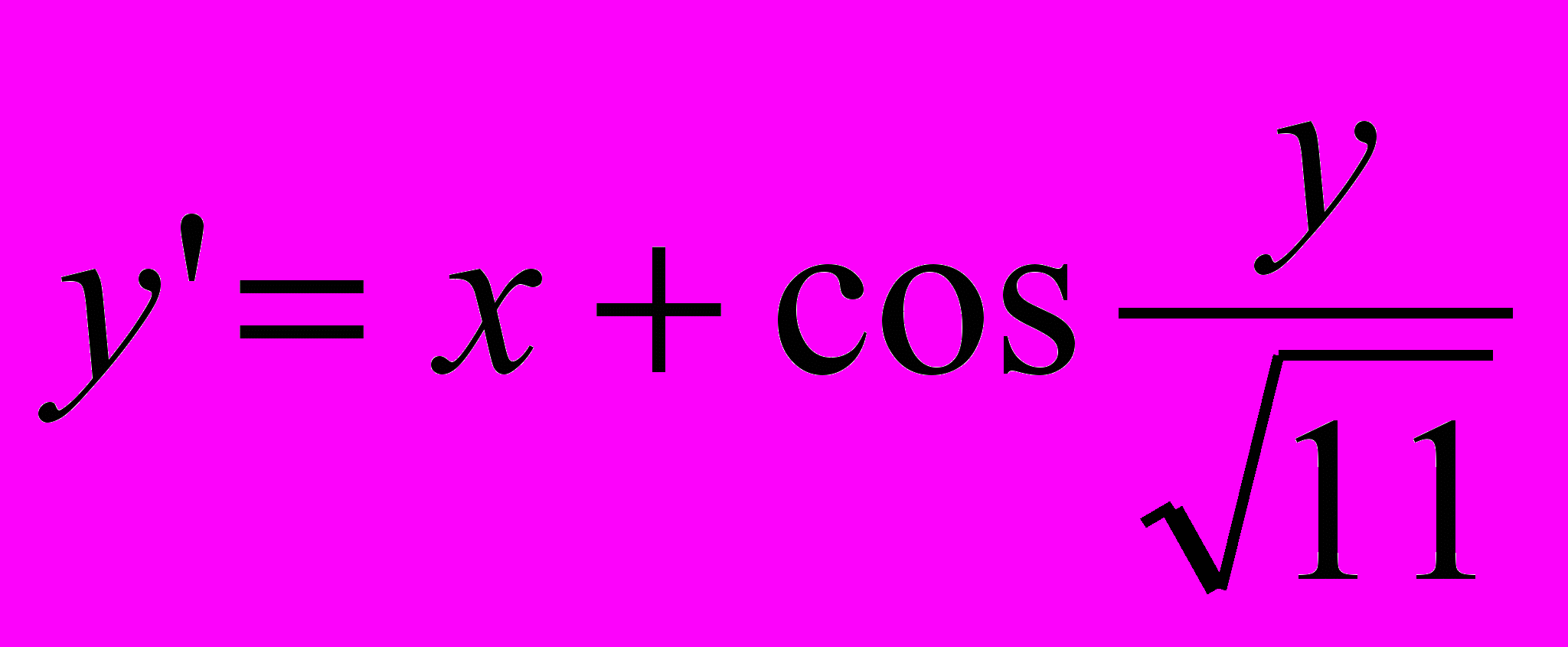


y0(2,1)=2,5
[2,1;3,1]

11


y0(1,8)=2,6
[1,8;2,8]

12


y0(1,6)=4,6
[1,6;2,6]

13


y0(0,6)=0,8
[0,6;1,6]

14


y0(0,5)=0,6
[0,5;1,5]

15


y0(1,7)=5,3
[1,7;2,7]

16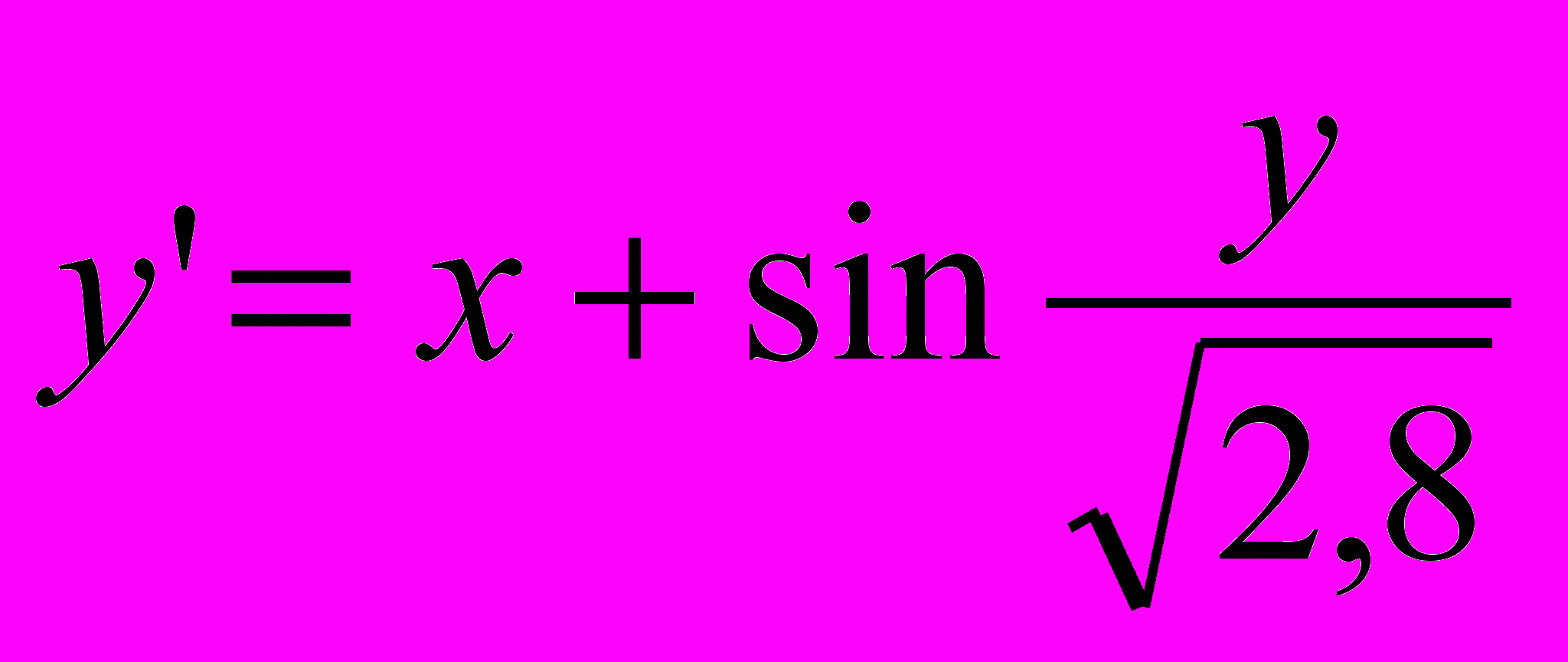


y0(1,4)=2,2
[1,4;2,4]

17


y0(0,8)=1,3
[0,8;2,8]

18


y0(1,1)=1,5
[1,1;2,1]

19


y0(0,6)=1,2
[0,6;1,6]

20


y0(0,5)=1,8
[1,8;2,8]