Метод сеток для приближенного решения задачи Дирихле

Вид материала

Документы

Подобный материал:

• Практических: 0 Лабораторных:, 21.53kb.
• Построение структурных сеток трёхмерных геологических сред произвольной топологии для, 27.27kb.
• Линейных алгебраических уравнений ax=B, где, 66.22kb.
• Метод прогонки решения краевой задачи для обыкновенного дифференциального уравнения, 49.69kb.
• Задачи и их решение Стандартные и нестандартные задачи Задачи «на работу» Задачи «на, 157.13kb.
• Решение уравнения теплопроводности Постановка задачи, 83.2kb.
• Темы курсовых работ по курсу «Программирование» для студентов группы биб-11-1 (2011-2012, 85.51kb.
• Тема курсовой работы, 36.24kb.
• Рабочей программы учебной дисциплины в. 3 Численные методы Уровень основной образовательной, 51.78kb.
• Рабочей программы учебной дисциплины в. 8 Численные методы Уровень основной образовательной, 55.63kb.

Тема5

Метод сеток для приближенного решения задачи Дирихле


Пусть - открытый прямоугольник на плоскости Oxy: x, y0
некоторые положительные числа.

Обозначим через  границу . Пусть в  функция u(x, y) непрерывна по совокупности переменных x, y и имеет в  непрерывные частные производные до второго порядка включительно.

Рассмотрим линейный дифференциальный оператор второго порядка

и применим его в  к функции u(x, y).

Как мы уже знаем, уравнение u=0 называется уравнением Лапласа. Если функция u(x, y) в области  удовлетворяет уравнению Лапласа, то эта функция называется функцией, гармонической в . Пусть точка

M(x, y). Поставим краевую задачу:



Будем считать, что f(P)- некоторая известная функция, непрерывная на . Поставленная краевая задача называется задачей Дирихле (или первой краевой задачей) для уравнения Лапласа.

Чтобы изложить суть метода сеток, сначала разобьем отрезок [0, a] точками на m частей, а отрезок [0, b] точками на n частей так, что каждый из участков разбиения имеет заданную длину h, 0i проведем прямые, параллельные оси Oy, а через точки y_j- прямые, параллельные оси Ox, так, чтобы весь прямоугольник  покрылся квадратами со стороной h. Эти прямые образуют сетку: x=lh, l=1,…,m, y=sh,s=1,…,n. Число h называется шагом этой сетки.

Точки пересечения прямых x=lh и y=sh называются узлами построенной сетки. В дальнейшем узлы сетки мы разделим на граничные, регулярные и нерегулярные. Наша цель- определить приближенные значения функции u(x, y) в узлах, находящихся на . Мы сделаем это, используя метод сеток (или метод конечных разностей), который состоит в следующем. Область непрерывного изменения аргументов x, y

(в нашем случае прямоугольник ) заменяется конечным (дискретным) множеством точек (узлов). Вместо функции u(x, y) непрерывно меняющихся аргументов x, y рассматривается функция u_h дискретного аргумента, определенная в узлах сетки. u_h называется сеточной функцией. Производные, входящие в уравнение Лапласа, заменяются (аппроксимируются) при помощи соответствующих разностных соотношений, т.е. линейных комбинаций значений сеточной функции в нескольких узлах сетки (ниже мы разъясним, как это делается). Дифференциальное уравнение u=0 при этом заменяется системой алгебраических уравнений (разностными уравнениями). Краевые условия заменяются разностными краевыми условиями для сеточной функции.

Рассмотрим конкретные значения чисел a, b и конкретную функцию f(P). Пусть a=3, b=2. Представим  как объединение четырех отрезков



Возьмем



(Задача. Проверить, что f(P) является на  непрерывной функцией.)


Зададим шаг сетки: h=0,6.


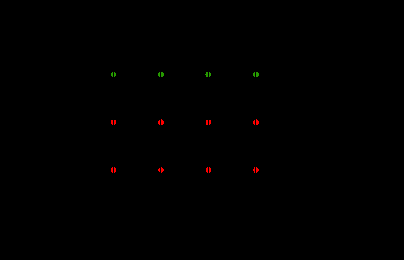Рис.1

Рассмотрим пятиточечный шаблон Ш («крест»):






Рис.2

Каждый из узлов (x-h, y), (x+h, y), (x, y-h), (x,y+h) называется соседним для узла (x, y).

Узел (x, y) построенной нами сетки называется регулярным, если все его соседние узлы принадлежат . Если хотя бы один из соседних для (x, y) узлов не принадлежит , то узел (x, y) называется нерегулярным. Точки пересечения сетки с границей  называются граничными узлами.

Занумеруем узлы сетки так, как это показано на рисунке 1.

Множество граничных узлов обозначим через ,

регулярных - R,

нерегулярных - NR.

В нашем случае имеем: узлы



Значения сеточной функции определим в узлах сетки по-разному в точках, принадлежащих R, NR. Положим



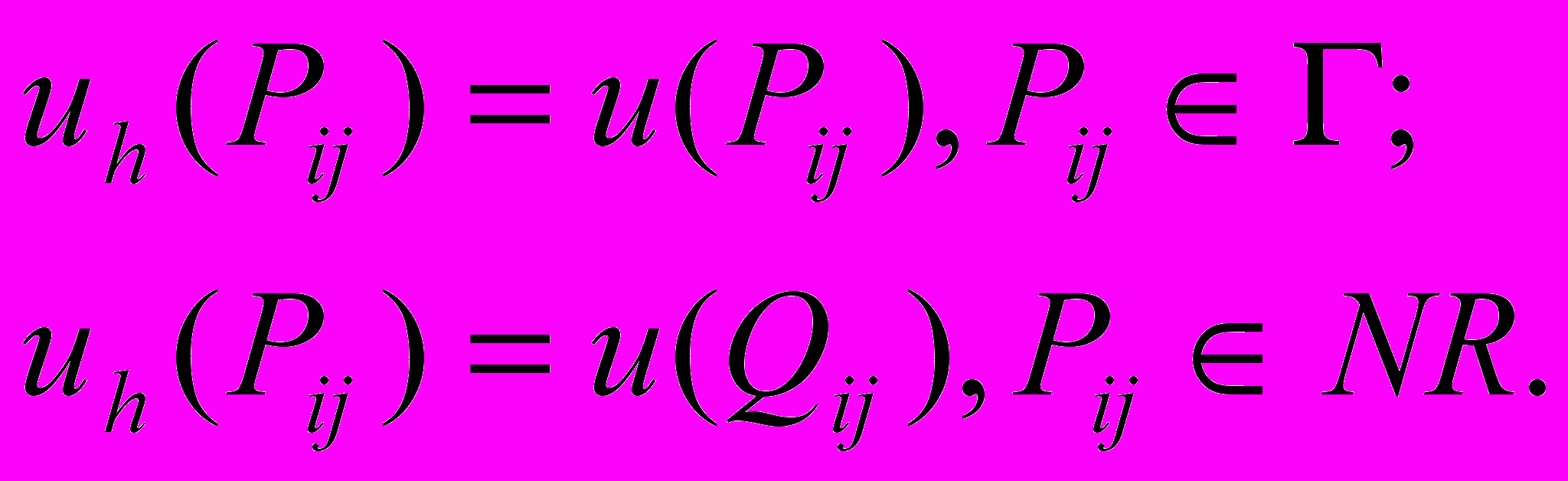
Значения u_h в регулярных узлах будут найдены из системы алгебраических уравнений, которую мы сейчас составим, и которая заменит собой дифференциальное уравнение Лапласа. Чтобы составить эту систему, воспользуемся указанным на рисунке 2 шаблоном Ш. Сначала составим, так называемые, восходящие и нисходящие разности, опираясь на определения частных производных 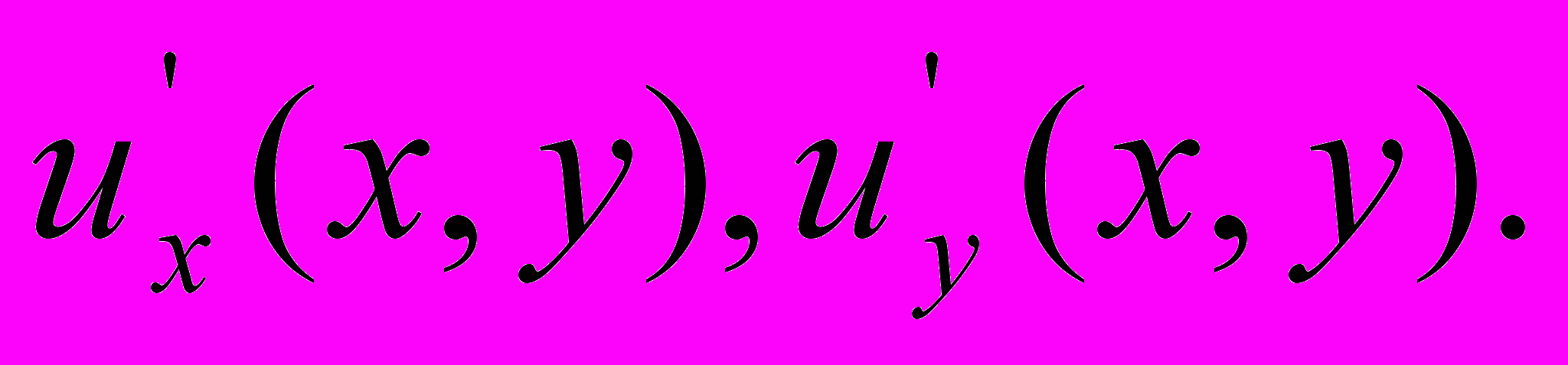Определим

восходящие разности;

нисходящие разности.

По определению частных производных имеем:



Воспользуемся нисходящими разностями и положим



Имеем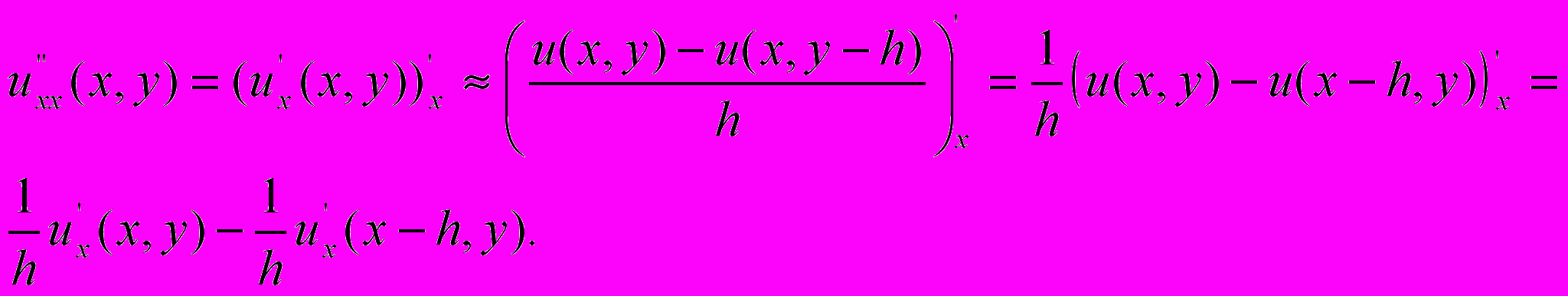



Воспользуемся восходящей разностью и положим теперь

так что



Аналогично полагаем, что



Таким образом, каждая из производных 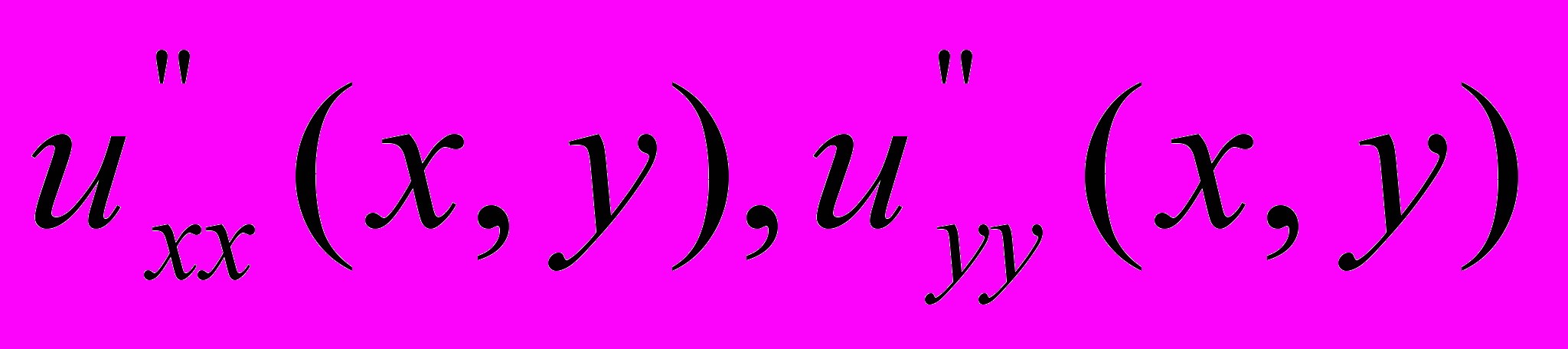приближенно равна линейной комбинации значений самой функции в узлах (x, y) и в соседних к ней узлах.

В уравнении Лапласа u=0 заменим частные производные второго порядка этими линейными комбинациями и получим, что



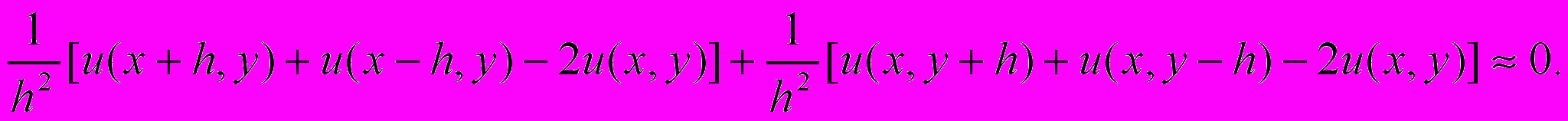
Отсюда получаем уравнение Лапласа в конечных разностях:

u(x+ h, y)+u(x-h, y)+u(x, y+ h)+u(x, y-h)-4u(x, y)=0.

Запишем это уравнение для каждого из узлов P_ijR. Сначала укажем координаты каждого из регулярных узлов:



Для точки P₁₁ имеем:



Для Р₂₁, Р₃₁, Р₄₁, соответственно, имеем:



Для Р₁₂, Р₃₂, Р₄₂, соответственно:



В полученной системе 8 линейных уравнений с 8 неизвестными (значениями u в регулярных узлах) заменим значения u в граничных и нерегулярных узлах по правилу, введенному ранее:



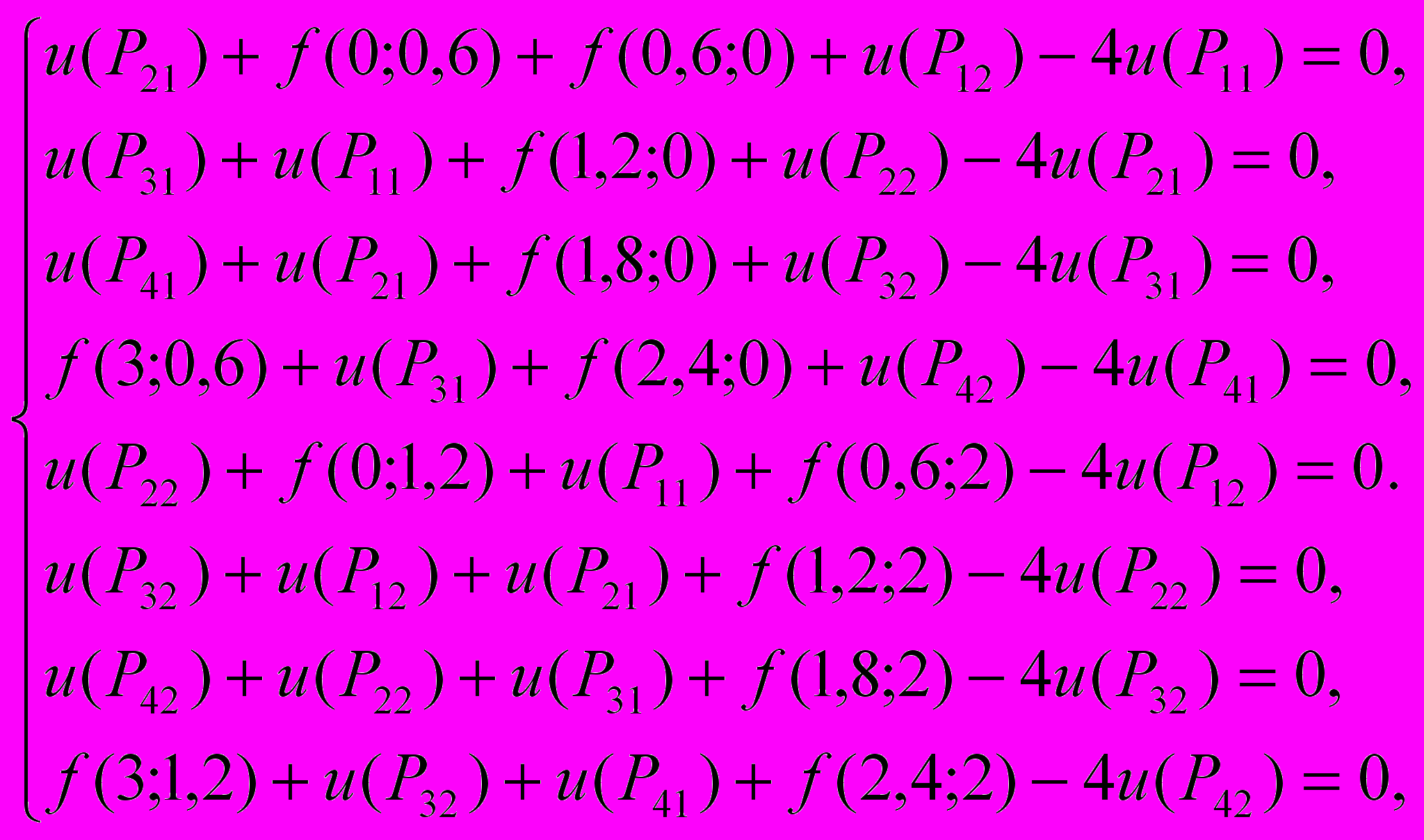
или



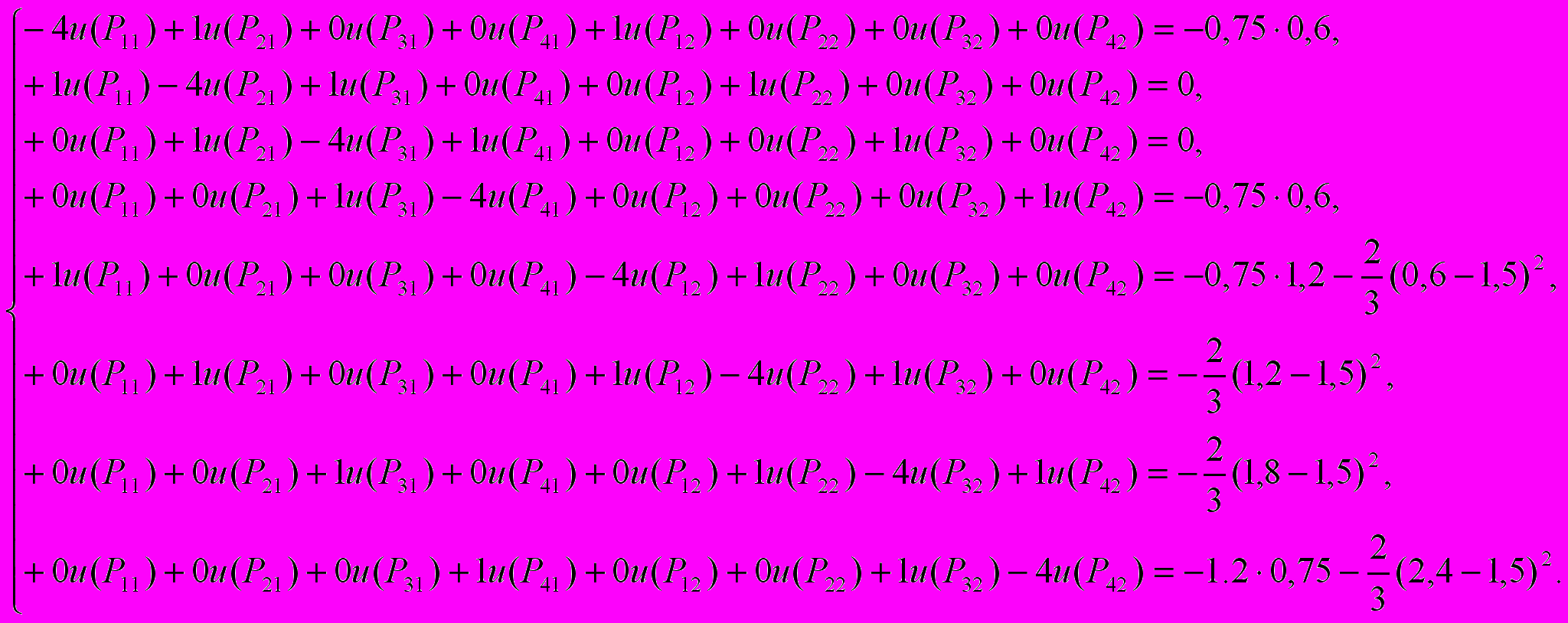
Запишем основную матрицу этой алгебраической системы:



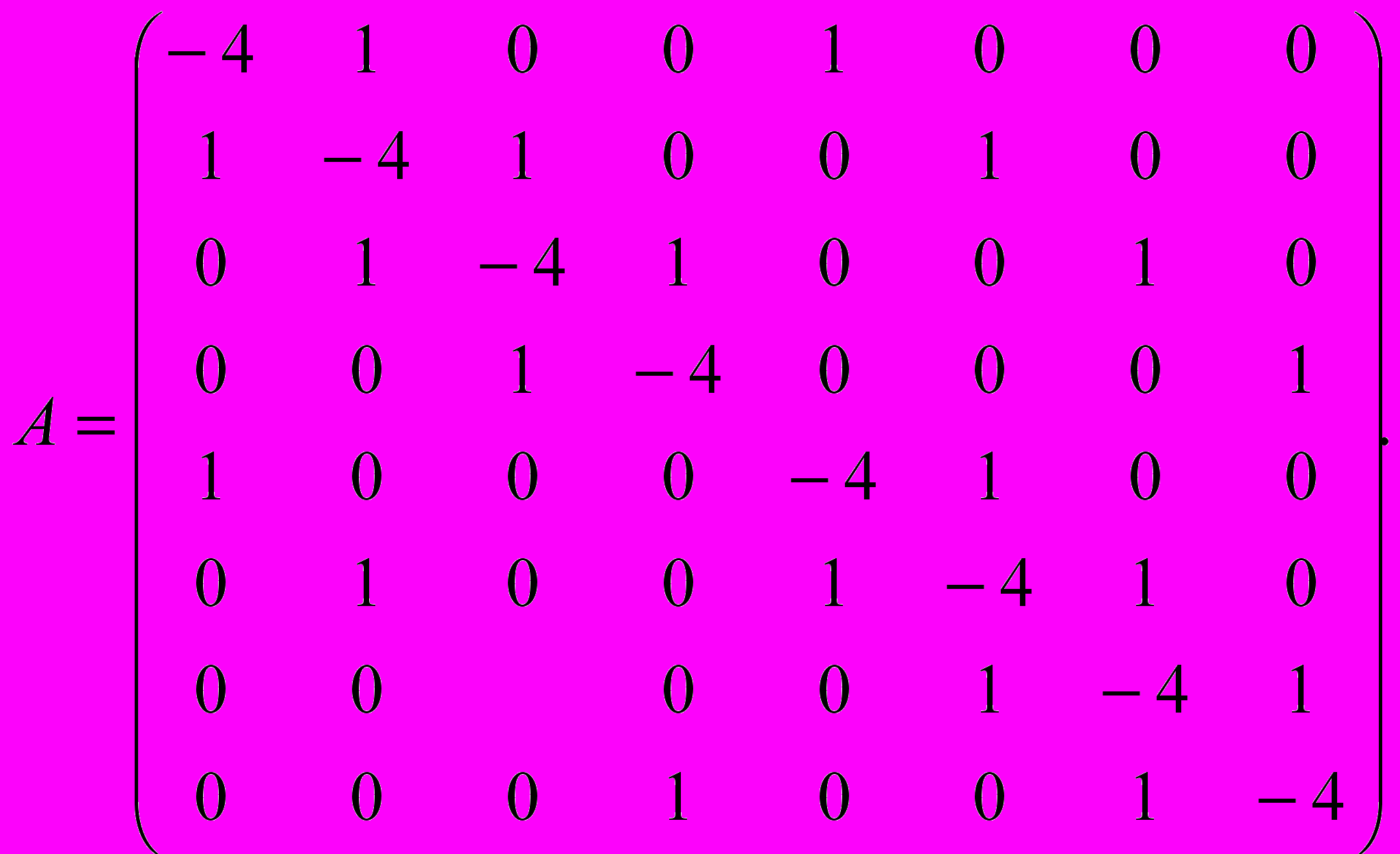
Столбец из свободных членов:



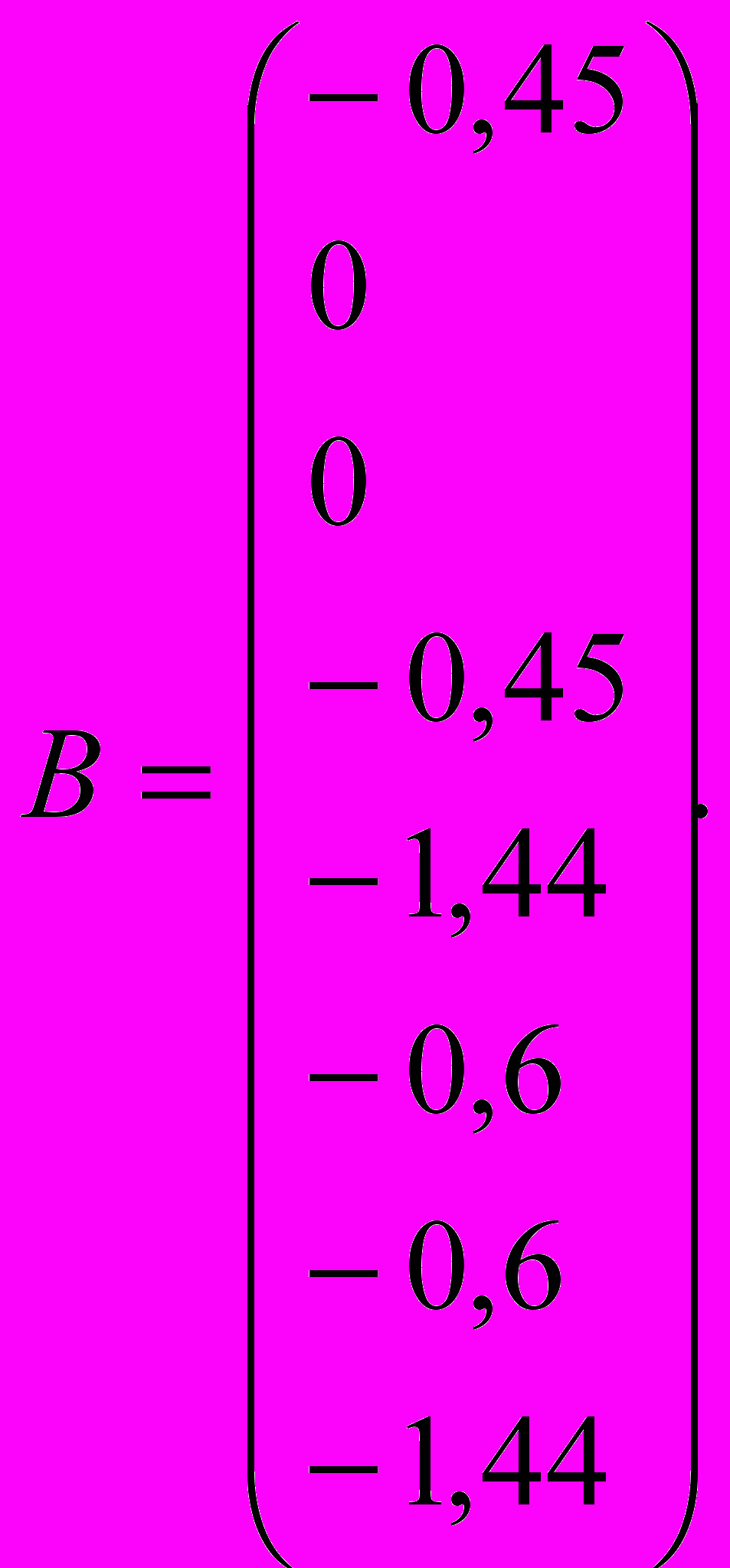
Рис.3

Решая систему с помощью указанной на рисунке 3 (или другой) программы, получим ее решение:

u(P₁₁)=0,278, u(P₂₁)=0,173, u(P₃₁)=0,173, u(P₄₁)=0,278, u(P₁₂)=0,490, u(P₂₂)=0,241, u(P₃₂)=0,241, u(P₄₂)=0,490.


Замечание. Для упрощения записи в системе значения сеточной функции мы обозначали через u, опустив индекс h.


Литература та же, что в теме 1.