Метод прогонки решения краевой задачи для обыкновенного дифференциального уравнения второго порядка c:\users\group\nof\lab11. mcd

Вид материала

Лабораторная работа

Подобный материал:

• Экзаменационные вопросы по курсу "Численные методы математической физики", 57.77kb.
• Задача Коши для неоднородного уравнения с однородными граничными условиями, 80.58kb.
• Решение дифференциального уравнения первого и второго порядка методом Рунге-Кутта 4-го, 55.71kb.
• Численное решение обыкновенных дифференциальных уравнений, 10.66kb.
• Вопросы к экзамену по учебной дисциплине «Дифференциальные уравнения», 32.43kb.
• Экзаменационные вопросы по курсу «Высшая математика, часть 6» для студентов второго, 21.39kb.
• Линейных алгебраических уравнений ax=B, где, 66.22kb.
• Программа курса лекций по методам математической физики, физико-химический факультет, 40.42kb.
• Программа курса лекций по методам математической физики, физико-химический факультет, 35.72kb.
• Задача Коши для квазилинейных дифференциальных уравнений в частных производных первого, 30.67kb.

Лабораторная работа №11


МЕТОД ПРОГОНКИ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ

ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО

ПОРЯДКА


C:\USERS\GROUP\NOF\lab11.mcd


11.1. Цель работы. Освоить метод прогонки решения краевой задачи для дифференциального уравнения второго порядка.


11.2. Справочный материал. При применении метода конечных разностей к крае­вым задачам для уравнений второго порядка получается “трехчленная система” линейных алгебраических уравнений, каждое из которых содержит три соседних неизвестных. Для решения такой системы разработан специальный метод, называемый методом прогонки. Рассмотрим линейное дифференциальное уравнение





на интервале [a,b] с условиями на границе





От уравнения (11.1) перейдем к конечно-разностному. Для этого:

1. Дискретизируем задачу, т.е. вводим сетку по переменной x:





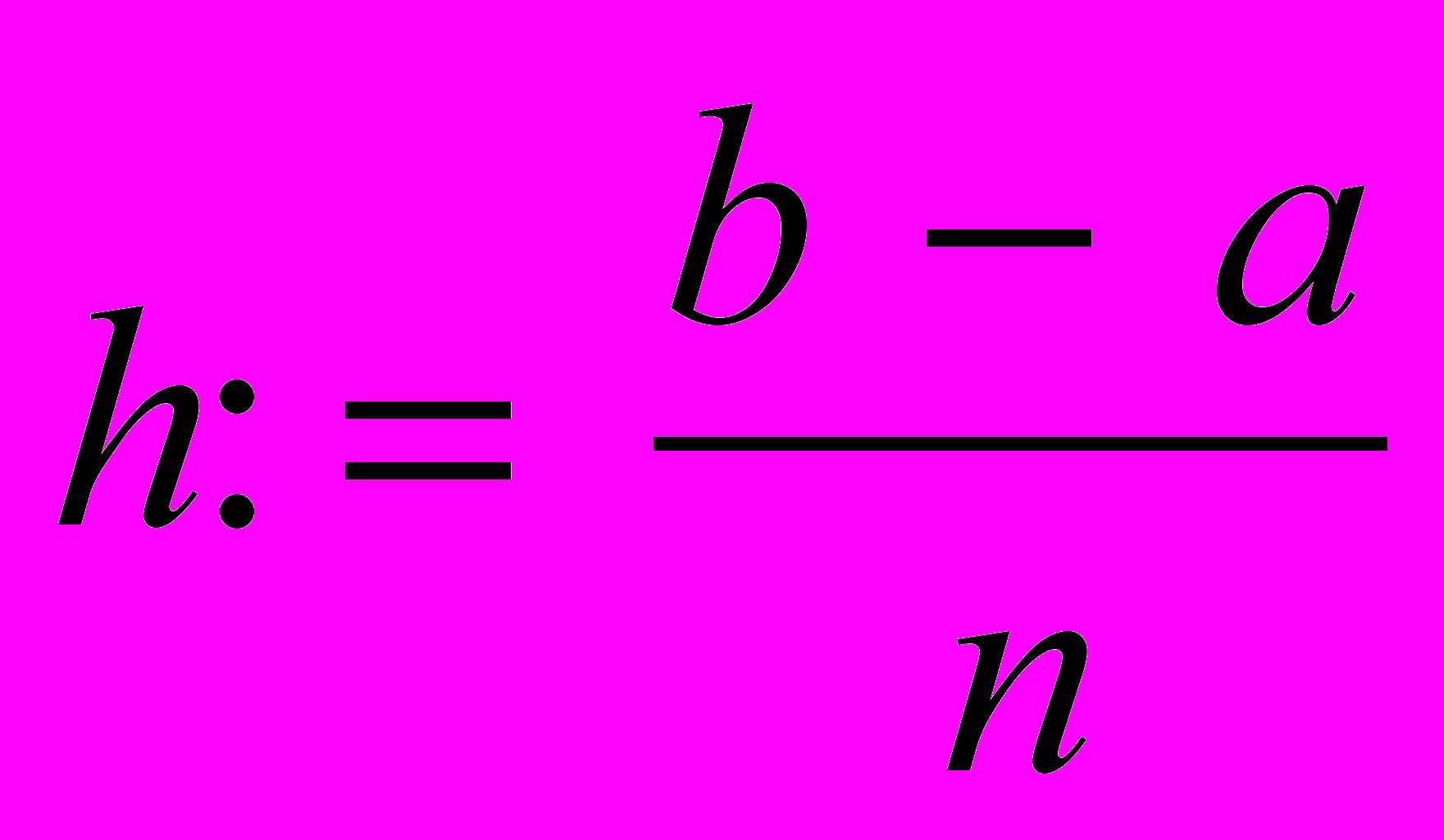
i:=0... n








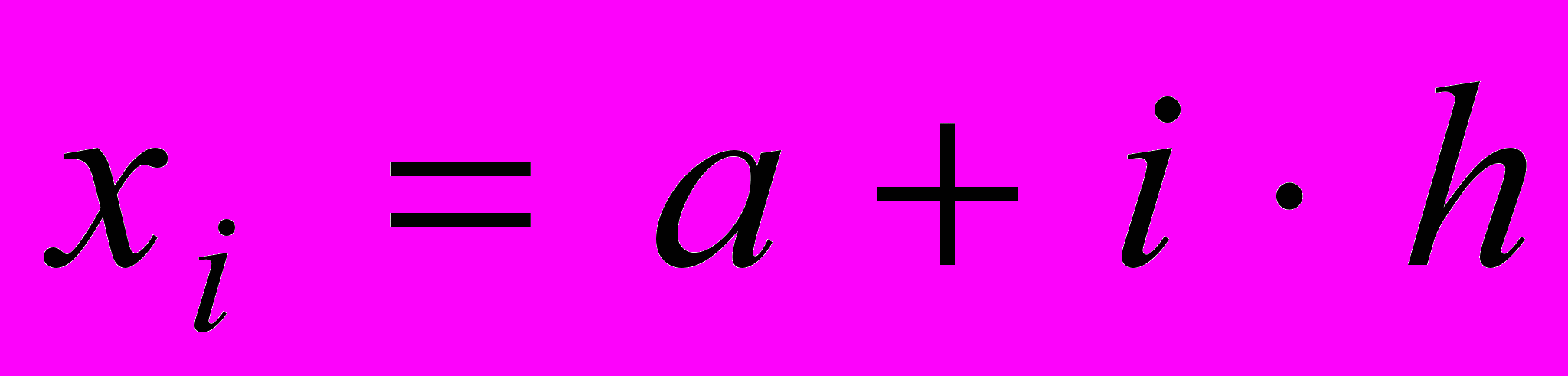
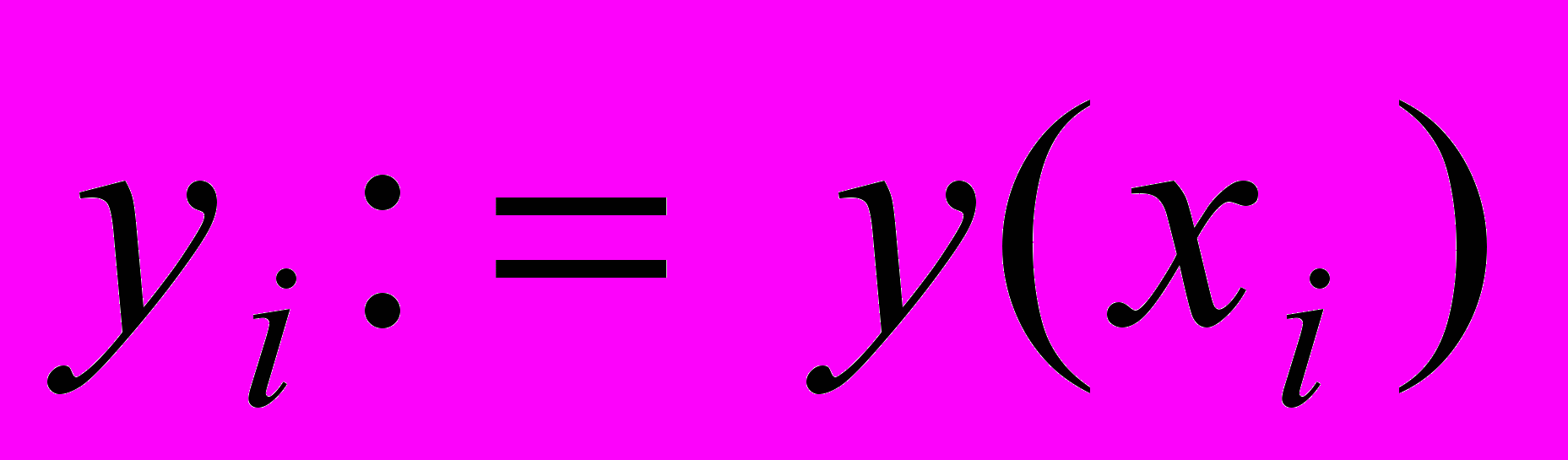
2. Заменяем исходное уравнение (11.1) конечно-разностным во внутренних узлах:




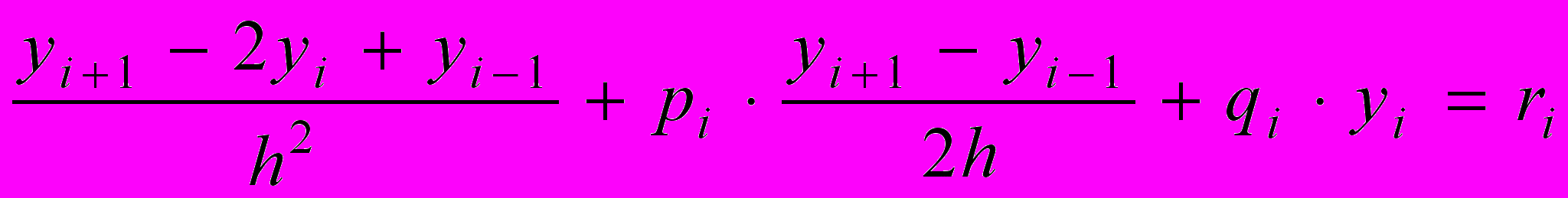
Это уравнение приводим к каноническому трехдиагональному виду





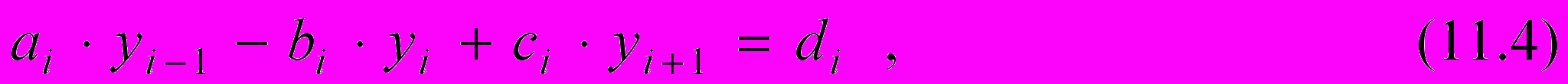
где




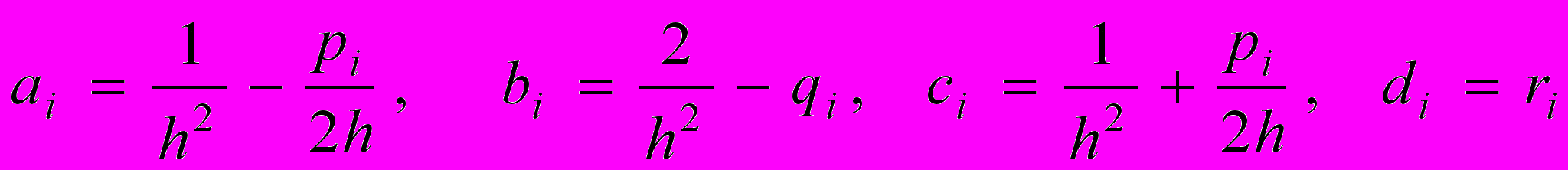
Линейную систему (11.4) можно решать обычным способом, однако более короткий путь - использовать метод прогонки. В этом случае решение ищется в виде



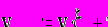
j = n, n - 1,...2 (11.5)

где x_j , h_j - прогоночные коэффициенты, которые необходимо предварительно вычислить. Решение реализуется в два этапа.


1. Прямой ход – от левого края заданного интервала [a,b] до правого в узлах сетки вычисляются x_j , h_j , j = 1, . . .,n

2. Обратный ход – от правого края до левого по формуле (11.5) в тех же узлах находится искомое решение.

Прямой ход реализуется рекуррентными формулами для прогоночных коэффициентов, которые получаются из (11.4) и (11.5) при k=1..n-1:


,


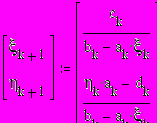Начальные значения коэффициентов для этих рекуррентных формул можно найти из (11.5) и левого краевого условия (11.2):




После того как получены прогоночные коэффициенты, можно приступать к обратному ходу по формуле (11.5), но предварительно необходимо найти значение 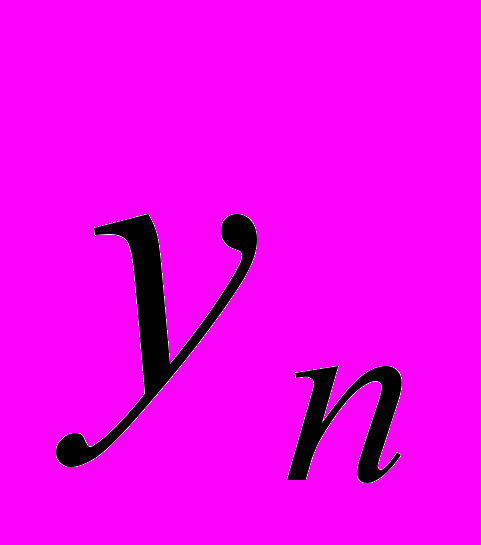. Из (11.5) и правого краевого условия (11.3) получаем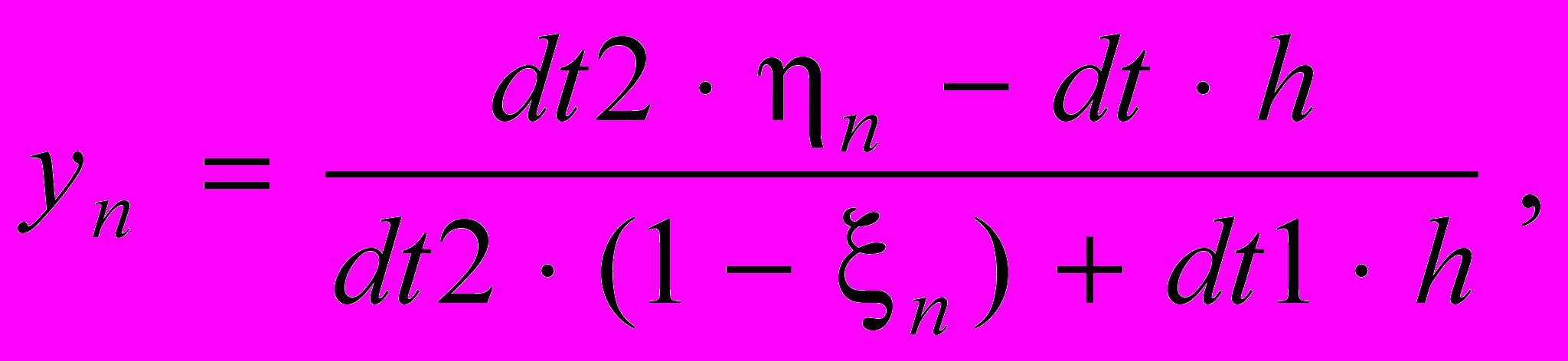



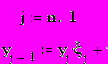а, теперь, собственно обратный ход - искомую функцию находим по рекуррентной формуле


11.3. Пример. Использование этого метода рассмотрим на примере краевой задачи для уравнения



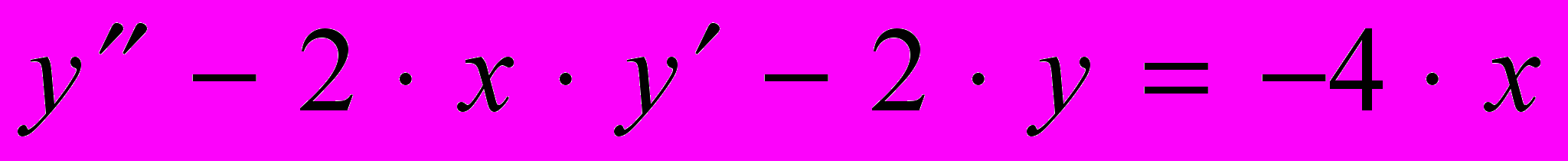
на интервале [0,1] с граничными условиями





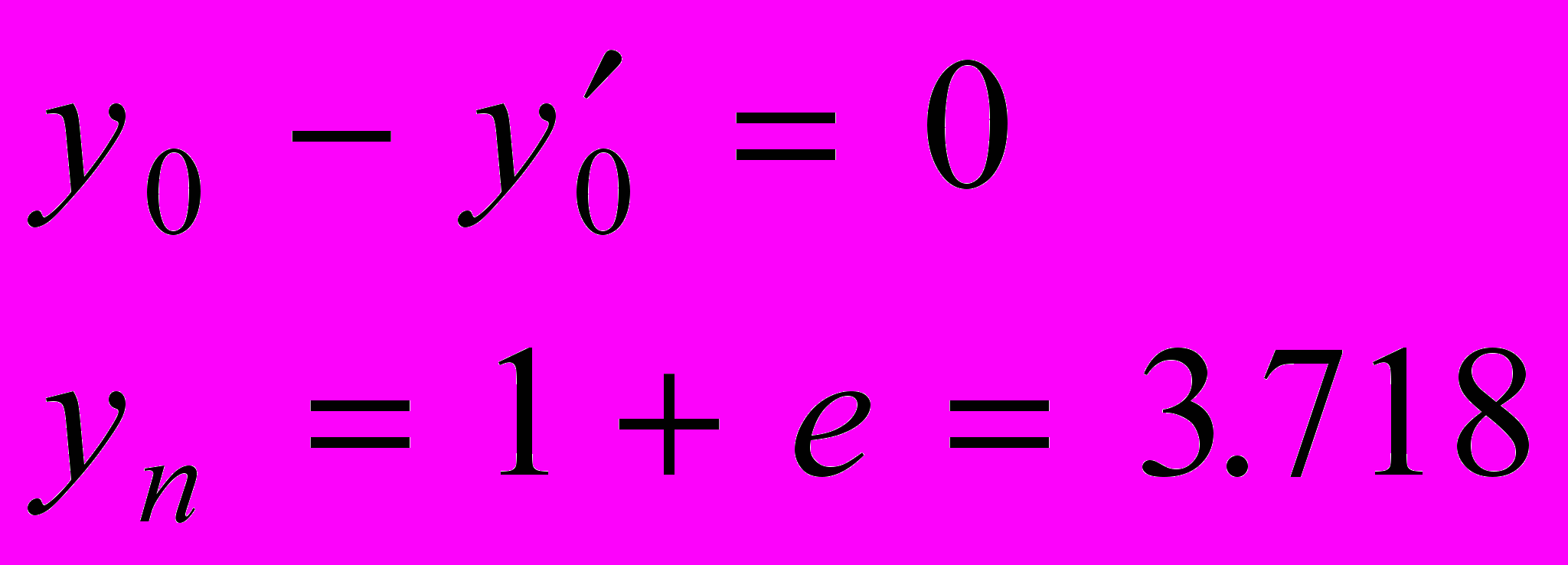
Замечание: данное уравнение имеет точное решение





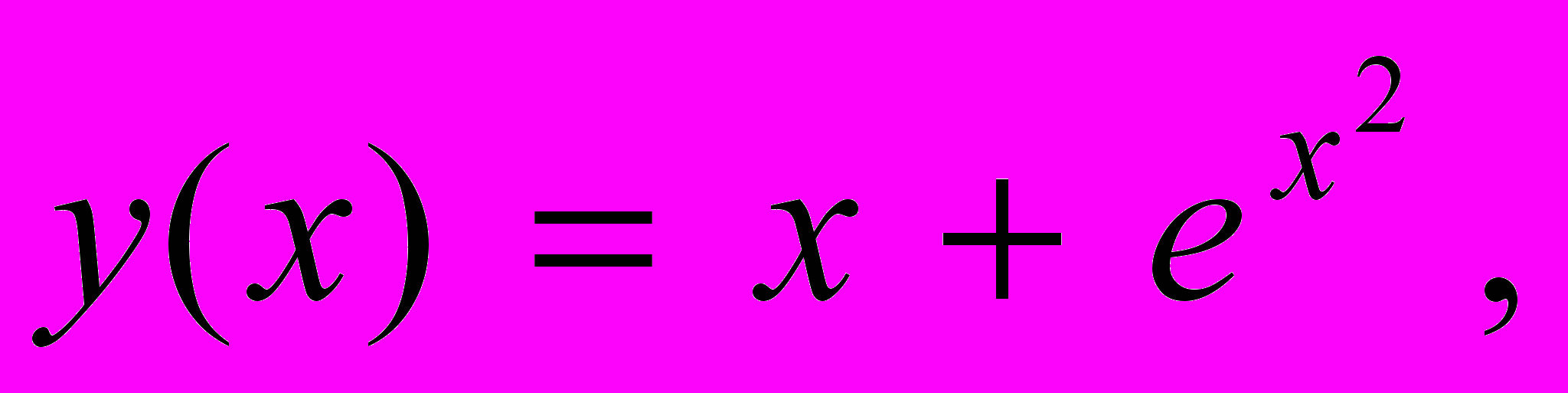
которое будет служить тестом для отладки программы.


11.3.1. Прямой ход










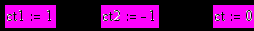
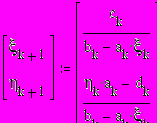
11.3.2. Чтобы начать обратный ход прогонки найдем из правого краевого условия:

dt1=1, dt2=0, dt=1+e


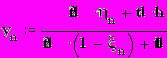
и граничное значение искомой функции


11.3.3. Обратным ходом рассчитываем значения функции в остальных узлах:





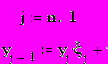
Полученное решение можно представить графиком





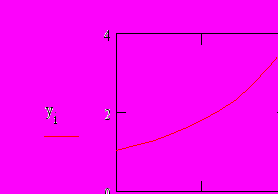
Для сравнения построим точное решение




Вычислим относительную погрешность:





Результаты численного и точного решения и погрешность приведем в таблице




11.4. Задание. Используя метод конечных разностей решить краевую задачу для обыкновенного дифференциального уравнения


1. ; ; .


2. ; ; .


3. ; ; .


4. ; ; .


5. ; ; .


6. ; ; .

7. ; ; .

8. ; ; 2 y(1.5) - 0.5.

9. ; ; .


10. ; 2 y(1.3) - ; .


11. ; ; .


12. ; ; y(0.7) +

13. ; ;

14. ; ; .


15. ; ; .


11.5. Вопросы для самопроверки.


1. В чем смысл краевой задачи при решении дифференциальных уравнений?


2. Каким образом метод конечных разностей сводит краевую задачу к системе линейных уравнений?


3. Почему в рассмотренном примере погрешность максимальна на левом конце интервала и уменьшается к правому концу?