Если использовать разности высших порядков вплоть до n-го, то разностное уравнение 1

1   2   3   4   5   6   7

90

форму разности между начальным значением оценки г/(0) и на­чальным состоянием процесса ;/_(| Подобные же квадратичные формы, оценивающие погрешность модели и измерений, содер­жатся в подынтегральном выражении функционала. Матрицы •Ро"¹, R и Q определяют весовые коэффициенты, оценивающие важность той или иной составляющей ошибки. Пусть e(t), r\(t)—случайные процессы типа белого шума, не коррелиро­ванные друг с другом и со случайным вектором |, а их средние значения равны нулю В качестве матрицы Р₀ берут матрицу ковариацнй случайной помехи £, оценки начального состояния:



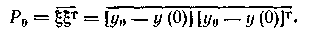
Здесь черта, как и ранее, соответствует операции взятия мате­матического ожидания. В этом частном случае, когда состав­ляющие вектора £, не коррелированны друг с другом, матрица Р₀ диагональная, и ее элементами являются дисперсии отдельных составляющих вектора | Аналогично матрицы весовых коэф­фициентов /?(/) и Q(/) обратны матрицам ковариащш процес­сов e(t) и т] (/):



По диагоналям этих матриц стоят корреляционные функции отдельных составляющих процессов е(1) п ц (I),а на остальных местах — взаимнокорреляционные функции двух разных состав­ляющих этих процессов. Элементы ковариационных матриц слу­чайных ошибок отражают неопределенность наших знаний. Чем больше эта неопределенность, тем с меньшим весом входит со­ответствующее слагаемое в критерий /.

Для решения задачи о минимуме / удобно ввести новую пе­ременную



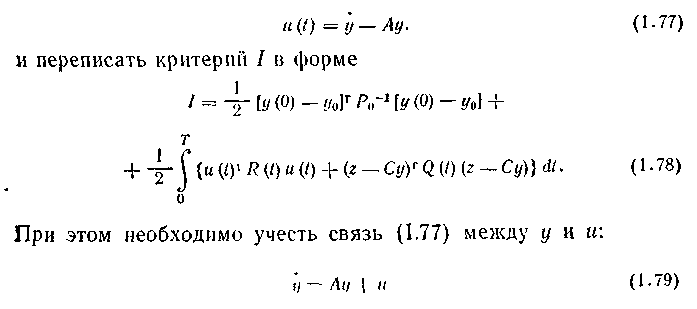
Функцию z(t) можно наблюдать; минимум ищется по ц(0) ну. Поставленная задача выпукла, поэтому ее решение существует и является единственным В соответствии с процедурой принци-


91

па максимума [40] запишем для задачи (1.78), (1.79) функцию Гамильтона



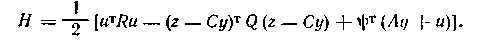
и потребуем ее стационарности по и (для выпуклой дифферен­цируемой функции максимум достигается в точке стационар­ности) :



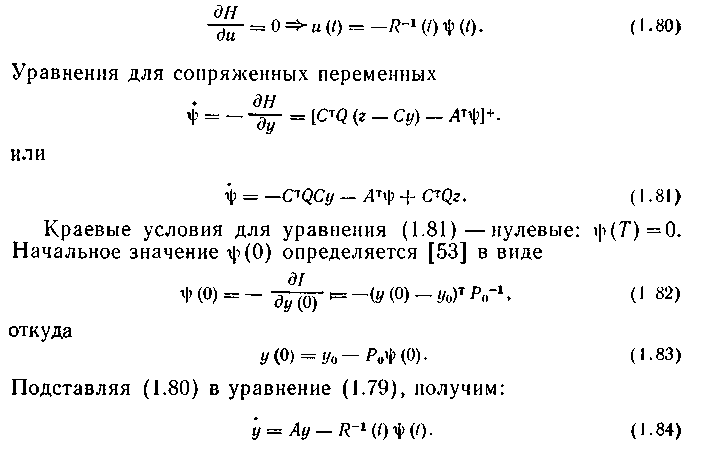
Таким образом, для вычисления оптимальной оценки у* (t) со­стояния процесса необходимо решить совместно уравнения (1.81) и (1.84), причем для уравнения (1.81) заданы условия в конце интервала наблюдения при t — T, а для уравнения (1.84) начальные условия определены через г|з(0). Так как граничные условия для у и ij) заданы на разных концах интервала наблю­дения, то одно из уравнений нужно решать в прямом времени, а другое — в обратном. Однако поскольку у входит в правую часть уравнений (1.81), a t|) —в правую часть уравнений (1.84), подобная процедура затруднена. Чтобы «развязать» систему (1.81), (1.84), удобно перейти к вспомогательным переменным b и ввести вспомогательную матрицу Р, так что




92

Подберем теперь вспомогательную матрицу Р так, чтобы в (1.87) сумма слагаемых, содержащих фи обратилась в нуль. Эта сумма равна

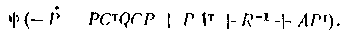
Условие ее равенства пулю приводит к дифференциальному уравнению для матрицы Р:

Если матрица Р удовлетворяет уравнению (1.88), то из равен­ства (1.87) вытекает уравнение для расчета вектора b(t):

Начальные условия для уравнений (1.88), (1.89) следует из на­чальных условий (1.82) для г|). Действительно, требование

Уравнения (1 88) и (1.89) не содержат в правых частях ника­ких других неременных, кроме Р, b и наблюдаемого вектора z. Они могут быть проинтегрированы в прямом времени от / = 0 до i = T. Это но позволяет выразить г|з(/) через у(1) в соответствии с (1.85), найти у(Т)=Ь(1) и переписать уравнение (1.86) в виде



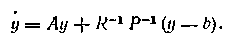
Решение этого уравнения в обратном времени определит ис­комую оценку y(t).

Однако полученная оценка может быть найдена лишь для тех моментов t, которые лежат внутри интервала наблюдения (О, Т). Часто требуется оценить вектор состояния в момент Т или даже прогнозировать его значение на т вперед. В первом случае оценка вытекает непосредственно из условия г|)(Г)=0, т. _е. y(t) (где / — текущий момент времени, совпадающий скоп­цом интервала наблюдения) получается из решения уравнения (1.89) заменой в нем b(t) на y(t):



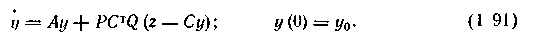
Здесь матрица Р определяется уравнением (1.88).

Прогнозирующую оценку у(1 + т;) получают из уравнения (1.91) интегрированием его до момента /+т. При этом начиная с момента t до t+ч матрицу Q(t), определяющую веса погреш­ностей измерения, полагают равной пулю (измерения отсутству­ют, их неопределенность сколь угодно велика), т. е. на участке


93