Geum.ru

Если использовать разности высших порядков вплоть до n-го, то разностное уравнение 1

Вид материалаДокументы

Содержание


К имеет неполный ранг, если нельзя выделить ни одного определителя той же размерности, что и у
R(p)=—Si, интегрального (И-) R(p) =
Оценка возможностей использования одноконтурных АСР.
Подобный материал:
1   2   3   4   5   6   7

70

и по имеющимся приближенным аналитическим моделям. Ана­логичную оценку можно дать предельным и среднеквадратич­ным отклонениям Ас и ос, AL и oL.

Анализ статических связей между переменными. Цель такого анализа — выявление статически независимых управляющих воздействий и регулируемых параметром

Связи между различными переменными могут возникать вследствие выполнения условий материального и теплового баланса, действия тех или иных физико-химических законов.

Например, при регулировании уровня в емкости массовые расходы поступающей и отводимой жидкости в статическом режиме должны быть равны, а уровень в емкости должен быть постоянным. Таким образом, только один из двух расходов является независимым. Если па входе в емкость и па выходе из нее имеется несколько потоков, то условие соблюдения ма­териального баланса уменьшает число независимых расходов на единицу. В кубе ректификационной колонны концентрация и температура жидкости при постоянном давлении связаны в статическом режиме однозначной зависимостью, так как кубо­вая жидкость находится в состоянии кипения.

Связи между выходными переменными возникают еще и потому, что в системе регулирования часть из них вычисляют, используя значения других переменных. Например, массовый расход газа рассчитывают, используя его объемный расход, температуру, давление и т.п.

При выборе структуры системы регулирования ограниче­нием является следующее правило: неременные, подлежащие стабилизации, следует выбирать таким образом, чтобы они были статически независимы друг от друга, т. е. чтобы в ста­тическом режиме ни одна из них не определялась значениями других.

Так, в кубе ректификационной колонны нельзя регулиро­вать температуру 0 и концентрацию с. с помощью двух регуля­торов. В качестве регулируемых переменных может быть вы­бран уровень и одна из величин — с или О

Нарушение указанною правила приводит к статической переопределенности системы. Даже если задания регуляторам согласованы со связью между переменными, т. е. условия y1= y01 и удовлетворяют объективно существующей связи



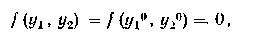
система окажется неработоспособной, ибо неизбежные ошибки в задании y°i и у°г приведут к тому, что равенство f(y°i,y°2) = -=0 не будет выполнено Последнее означает, например, что емкость, у которой стабилизированы расходы на входе и вы­ходе, постепенно переполнится пли опустеет, несмотря па то, что стабилизаторам расходов установлены одинаковые зада­ния. Поэтому стабилизировав можно лишь один расход и не-


71




зависимый от него в статическом режиме уровень в емкости.

Для того чтобы технологический
процесс был статически управляем,
нужно, чтобы число независимых,
управляющих воздействий было не меньше числа стабилизи­
руемых переменных (т. е. если размерность вектора и окажет­
ся меньше размерности статически независимых составляющих
вектора у, то некоторые составляющие у невозможно будет
скомпенсировать изменением и). *

Однако и в том случае, когда размерность и больше раз- мерности у, объект может оказаться статически неуправляе- ' мым, если матрица К коэффициентов усиления, связывающих в статике векторы у и и, имеет неполный ранг.

В статике в линейном приближении векторы и к у связаны
соотношением у = Ки, где К — матрица коэффициентов усиле­
ния передаточных функций Wu. Для объекта, астатического
по некоторому каналу, в матрице К. коэффициент усиления по-
лагают сколь угодно большим.

Матрица К имеет неполный ранг, если нельзя выделить ни одного определителя той же размерности, что и у, отличного от нуля. Геометрически это означает, что изменения вектора у, связанные с изменениями управлений, лежат в пространстве Y в некоторой плоскости, и только те возмущения, которые вы­зывают отклонения у в этой плоскости, могут быть скомпенси­рованы управляющими воздействиями.

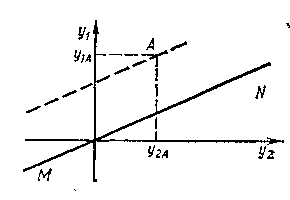
Пример. Пусть связь между векторами у и и имеет форму



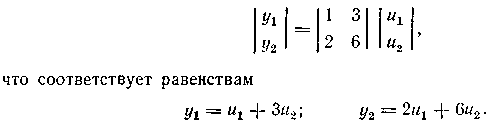
Изменения управляющих воздействий вызывают только такие изменения y1 и y2, при которых Д(/|/Д(/2=0,5. Таким образом, вектор у может в результа­те изменения и меняться вдоль прямой MN или прямых, параллельных ей. Если в результате действия возмущений значения y1 и y2 оказались рапными У\л и г/2,4 (рис. 1.51), то изменением и нельзя возвртить вектор у и начало координат.

Если размерность у равна двум, а размерность и — трем, связь между и и w в статике имеет форму




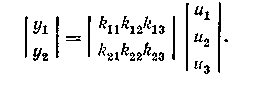
72

Объект статически управляем, если хотя бы один из опреде­лителей



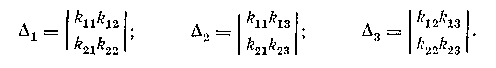
отличен от пуля.

Анализ статики объекта по каналам возмущений позволяет в ряде случаев уменьшить число регулируемых переменных. Связь между составляющими у и возмущениями z в статике имеет форму



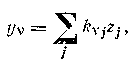
где kvi — коэффициенты усиления по каналам возмущения. Если выполнено неравенство



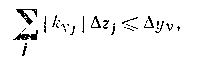
то возмущающие воздействия не вызывают статического от­клонения yv, большего, чем это допустимо. Динамические же отклонения yv, как следует из передаточных функций (1.49),




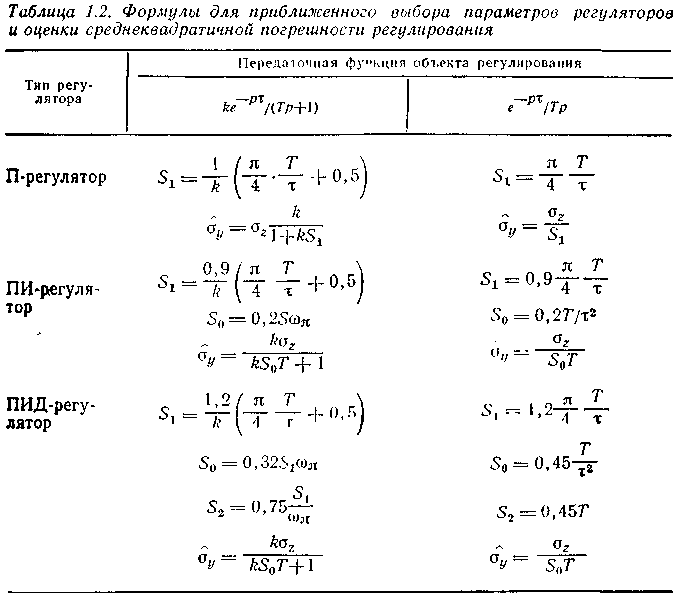
73





(1 50), заведомо меньше Ду. Таким образом, нет необ­ходимости в специальном регуляторе для стабилиза­ции yv

После синтеза системы регулирования следует проверить, не приведут ли изменения управляющих воздействии к суще­ственным отклонениям yv в результате взаимосвязанности ка­налов регулирования.

Выбор параметров регуляторов и оценка качества регулирова­ния. При выборе параметров передаточных функции типовых промышленных регуляторов:

пропорционального (П-) R(p)=—Si, интегрального (И-) R(p) =—S0/p,

пропорционально-интегрального (ПИ-) R(p) ——S"/p--St, пропорционально-интегрального с импульсом но производной (ПИД-) R(p)=—Solp—St— S2p

широко используют приближенные формулы (см. раздел 1.2), основанные на методике Циглера — Никольса Формулы, свя­зывающие настройки регуляторов S0, Si, S2 с характеристика­ми объекта, собраны в табл. 1.2. В этой таблице для статиче­ского объекта через wп обозначена частота, на которой АФХ объекта пересекает отрицательную действительную полуось (имеет фазовый сдвиг, равный я). Она является корнем урав­нения



Удобно находить wя по кривой, изображенной на рис 1.52.

В табл. 1.2 приведены верхние оценки а// для среднеквад­ратичного отклонения регулируемой величины при возмущаю­щем воздействии, имеющем дисперсию cr2z Эти оценки получе­ны следующим образом. Для замкнутой системы с ПИ- и ПИД-регуляторами, настройки которых выбраны по формулам табл. 1.2, амплитудно-фазовая характеристика приближенно запишется в виде -



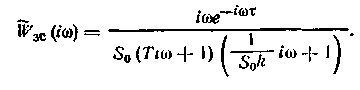
Известно, что при воздействии на систему случайного про­цесса со спектральной плотностью Sг(W) среднеквадратичная ;


74


ошибка выходной координаты у может быть, подсчитана как







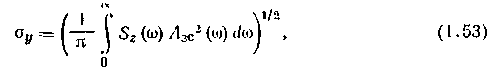
где Азс —АЧХ замкнутой системы

На этапе предварительного выбора структуры системы ре­гулирования спектральная плотность s2(w) неизвестна, но мож­но оценить ее дисперсию, связанною со спектральной плот­ностью, выражением







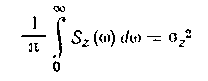
Для оценки ац сверху воспользуемся тем, что при заданной oz среднеквадратичное отклонение у максимально, когда вся энергия возмущающею сигнала сосредоточена на топ частоте, на которой функция Аc(a>) максимальна. Обозначим эту час­тоту Юр (она близка к рабочей частоте замкнутой системы) и примем



Подставляя это выражение в формулу (1.53), получим ау =

= ОгЛзс(о)р).

Для П-регулятора модуль АФХ замкнутой системы дости­гает максимума на частотах, близких к нулю, и равен для статического объекта



а для астатического объекта



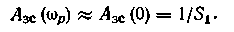
В системах с ПИ- и ПИД-регуляторами при выборе на­
строек по табл. 1.2 частота wр оказывается приблизительно
равной (S0k/T)i/2; тогда



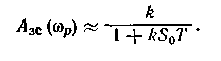
Эти величины и использованы для получения оценки средне­квадратичной погрешности.

Если возмущающих воздействии несколько, оценку для Оу можно подсчитать но тем же формулам, подставив



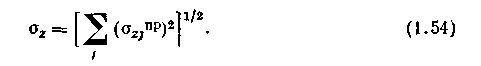
Здесь опр2; — среднеквадратичные значения возмущений, при­веденные ко входу предполагаемого капала регулирования.


75

Приведение осуществляется по формуле







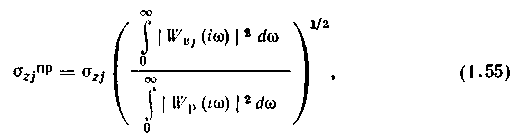
в которой W в, и W р — частотные характеристики объекта соот­ветственно по каналам возмущения и регулирования. Для ста­тического объекта с передаточной функцией WCT(p) =k/(Tp-{--И)е-Рт



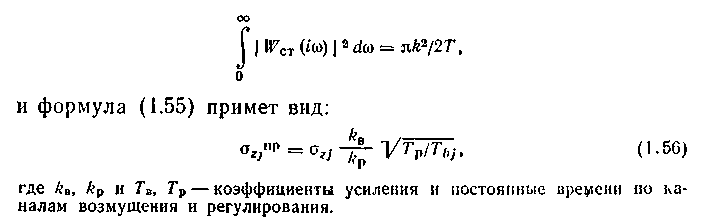
Оценка возможностей использования одноконтурных АСР.

Для выбора локальных контуров регулирования удобно резуль­таты расчетов свести в таблицу, характеризующую возможности использования тех или иных каналов регулирования. Для каж­дого из управляющих воздействий uv и регулируемых перемен­ных у, при тех или иных типовых законах регулирования в таблицу вносят отношение a, v рассчитанной оценки ау, к допу­стимому отклонению. Если это отношение оказывается больше единицы, или если между управлением wv и переменной у, нет связи, ставят прочерк. Таким образом, если прочерки стоят в какой-либо строке, это значит, что данное управляющее воз­действие неприменимо. Если же прочерки стоят во всех клет­ках некоторого столбца, это значит, что данный параметр нельзя стабилизировать с требуемой точностью с помощью од­ноконтурных АСР. Такие строкиi и столбцы на данном этапе исключаем из рассмотрения.




к допустимому отклонению Д«/;.


Наиболее простои закон регулирования — пропорциональ­ный, поэтому в первую очередь проверяем возможность ис­пользования П-регулятора. Показателем качества регулирова­ния в этом случае служит наибольшее из двух чисел — u;v • (отношение среднеквадрашчной ошибки к максимальному до­пустимому ее значению) или 3; v—отношение статической ошибки регулирования


76







При подсчете статической ошибки регулирования значения каждого из возмущений Az, приводят ко входу канала регули­рования из условия



и в формулу (1.57) подставляют наибольшее приведенное cтa-тическое возмущение. Такой подход правомерен, потому что вероятность статического отклонения одновременно нескольких возмущающих воздействий от номинальных значений па пре­дельную величину очень мала.

При выборе контуров регулирования каждой из регулируе­мых переменных у, нужно сопоставить одно из управляющих воздействий uv. При этом необходимо учесть, что одно и то же , управление нельзя использовать для регулирования двух или бо-
  • лее величин. Критерием правильности выбора контуров регули­
    рования может служить наибольшее значение показателя каче-
  • ства для выделенных контуров. При оптимальном выборе это
    значение должно быть возможно меньше.

Рассмотрим пример выбора одноконтурной АСР с П-регу­лятором (табл. 1.3). В отличие от показателей качества отдель­ных контуров регулирования введем показатель качества АСР процесса:



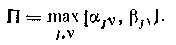
Требуется так выбрать управления и для каждой из пере­менных у,, чтобы, во-первых, значение II оказалось минималь­ным и, во-вторых, каждое управление было использовано лишь для одной регулируемой величины

Поставленная задача относится к так называемым задачам О назначениях, для решения которых при большой размерно-

сти у и и имеется целый ряд алгоритмов, ориентированных на использование ЦВМ. Однако при небольшой размерности этих векторов приемлемое решение можно наши с использованием следующей процедуры. 1-й шаг. Выбирают начальное приближение искомого ре-

шения. Для этого временно отбрасывают второе из приведенных

.


77

требований и для каждого у, находят управление, обеспечиваю­щее минимальное значение показателя качества одноконтурной АСР с регулятором данного типа (в табл. 1.3 соответствующие числа отмечены звездочкой). Максимальное из отмеченных зна­чений П (в табл. 1.3 оно равно 0,4 и соответствует контуру г/4~г/2) заведомо не превосходит Пщш Однако может оказаться, что одно и то же управление сопоставлено нескольким регули­руемым переменным (в табл. 1.3 оказалось, что и8 используется для регулирования г/2 и у5). Если такой ситуации не возникло, найденное решение удовлетворяет условиям задачи, и П* =

= Пщт.

2-й шаг. Для регулируемых переменных, которым оказа­лось сопоставлено одно управление, ищут подходящее среди «свободных» управлений, т. е управление, которое на первом шаге не сопоставлено ни одной из переменных у, п для которого показатель качества минимален В рассматриваемом приме­ре для у2 и г/5 находят «свободное» управление и7, которое при регулировании у2 может обеспечить показатель качества 0,4. Так как это значение не превосходит П1', задача решена, ибо показатель качества системы не ухудшился, а все ограничения выполнены.

Таким образом, структура системы определяется соответст­виями у2~и7; 3~«i; #4~«2; У5~«8, а Ятш = 0,4.

Прочерк в первом столбце табл. 1.3 говорит о том, что пара­метр г/i нельзя регулировать при использовании одноконтурной системы с П-регулятором. Для всех подобных переменных на следующем этапе составляют таблицу показателей качества при использовании ПИ-регулятора и аналогичным образом выбира­ют контуры регулирования. Затем, если необходимо, выбирают контуры регулирования с ПИД-регуляторами. Если в неко­торых столбцах таблицы стоят прочерки по всем управлениям для всех типов регуляторов, значит, необходимо использовать дополнительные средства улучшения качества регулирования. Предварительный выбор схемных методов улучшения качества регулирования. Среди методов повышения качества регулиро­вания за счет усложнения структуры систем регулирования наи­более распространены следующие:

1) введение импульса по пошущению; 2) введение динами­ческой компенсации в системах взаимосвязанного регулирова­ния; 3) использование каскадных АСР; 4) введение в АСР им­пульса по значению промежуточной координаты.

Подробно каждый из этих способов и выбор параметров кор­ректирующих устройств изложены в разделе 1.2 Здесь мы оста­новимся только на возможностях предварительной оценки по­лезности использования схемных методов повышения качества при выборе структуры системы.

Введение в систему регулирования импульса по возмущению целесообразно в том случае, если показатель качества а при выборе любого из типовых законов регулирования для данного


78

параметра оказался больше единицы, причем в формуле (1 54) для расчета среднеквадратичной величины приведенного возму­щения доминируют одно или два возмещающих воздействия, ко­торые доступны прямому или косвенному измерению. Такое введение полезно и тогда, когда одно из доступных измерению возмущении имеет значительное статическое отклонение Аг. При правильном выборе характеристик динамического компенсатора (см. разд. 1 2) их влияние существенно уменьшается, и соответ­ствующие слагаемые в уравнении (1.54) можно исключить. По­казатель качества регулирования при этом уменьшится (если он станет меньше единицы, соответствующее значение можно подставить в таблицу и использовать при дальнейшем анализе). В системах с взаимосвязанными параметрами регулирующие воздействия влияют не только па «собственную», но и на другие регулируемые переменные, являясь для них дополнительным» возмущениями, которые следует учитывать при расчете показа­телей качества регулирования и и [5 Сели вклад этих возмуще­ний в среднеквадратичную ошибку значителен и показатель ка­чества регулирования больше единицы, нужно ввести динамиче­ские компенсаторы, т е перейти к системе автономного регули­рования.

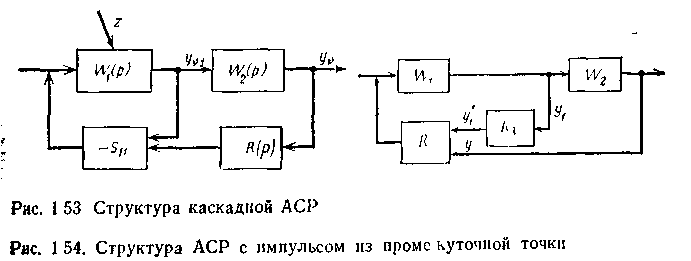
Если после компенсации влияния возмущений для регулиро­вания некоторых параметров нельзя использовать одноконтур­ную систему (т. е. соответствующие таблицы остались незапол­ненными), целесообразно оценить возможности каскадной АСР • (рис. 1.53). В этой системе (см. разд. 1.2.2) вспомогательный регулятор поддерживает на заданном уровне промежуточный параметр yv\, а основной регулятор меняет задание вспомога­тельному так, чтобы стабилизировать регулируемую величи-

vyVv

При использовании каскадной АСР возмущающие воздей­ствия z, влияющие на yv через изменение yvi, гасятся во внут­реннем контуре. Требования к статической ошибке поддержа­ния yvi обычно невысоки, и во вспомогательном контуре может быть использован П-регулятор с параметром настройки Sц, найденным по приближенным формулам (табл 1.2) для объек­та с передаточной функцией W\(p). С помощью той же табли-




79






цы можно оцепить oyi — средне­квадратичное отклонение проме­жуточной координаты.

Для вычисления среднеквад­
ратичного отклонения основной
регулируемой переменной сле­
дует перейти к эквивалентной
системе, в которой возмущающие
воздействия г заменены возму­
щением j/vi, влияющим на ;/v
через передаточную функцию
W 2(p) и имеющим дисперсию
о2,,! Передаточная функция эк­
вивалентного объекта W3 равна
произведению передаточной

функции системы регулирования t/v 1 на W2. Передаточная функция вспомогательного контура регулирования, содержащего П-регулятор, равна (см. табл. 1.2)



Аппроксимируя передаточную функцию эквивалентного объ­екта WB(p)W2(p) апериодическим или интегрирующим звеном с запаздыванием, оценивают 0tfv для одноконтурной системы (по формулам табл. 1.2) с тем или иным типом основного регулятора и рассчитывают соответствующие значения показателя качества.

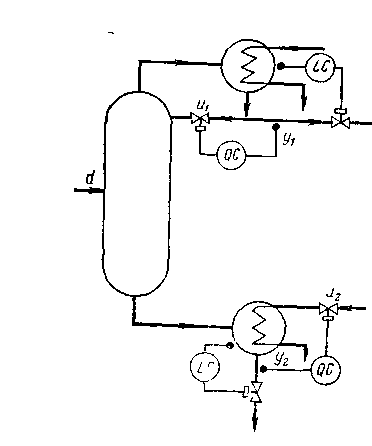
Для схемы с отбором импульса из промежуточной точки (рис. 1.54) параметры динамической связи, имеющей обычно вид реального дифференцирующего звена



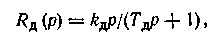
стремятся выбрать так, чтобы эквивалентный объект, выходом которого является сумма у\' + у, в статическом режиме вел себя как объект с передаточной функцией Wl(p)Wz(p), а при высо­ких частотах был близок к объекту с передаточной функцией Wi(p)kcITf. Если Wi'(P) и Wz(p) аппроксимированы аперио­дическими звеньями с запаздыванием, то передаточная функция эквивалентного объекта приближенно равна



По ней и выбирают параметры регулятора (с использованием формул табл. 1 2) и рассчитывают <зу и соответствующее значе­ние а.