Если использовать разности высших порядков вплоть до n-го, то разностное уравнение 1
| Вид материала | Документы |
- Частные производные и дифференциалы высших порядков п. Частные производные высших порядков, 190.6kb.
- Статья Тема: «Уравнения высших степеней с параметрами», 55.64kb.
- § Тема. Некоторые определения и обозначения, 1005.59kb.
- Статьи на русском, 122.97kb.
- Решение кубического уравнение в общем виде. От общего кубического уравнения к упрощённому, 14.77kb.
- У (к = 1,2,…). Однако на практике часто выгоднее выражать значения производных не через, 96.45kb.
- Содержание уравнения математической физики (нм-3) Уравнения математической физики (нп-3), 92.05kb.
- Определители 2-го и 3-го порядков: определения и применение к решению систем линейных, 42kb.
- Диффузия в биологических системах. Диффузия, 145.79kb.
- Методические рекомендации студентам, 215.81kb.
61
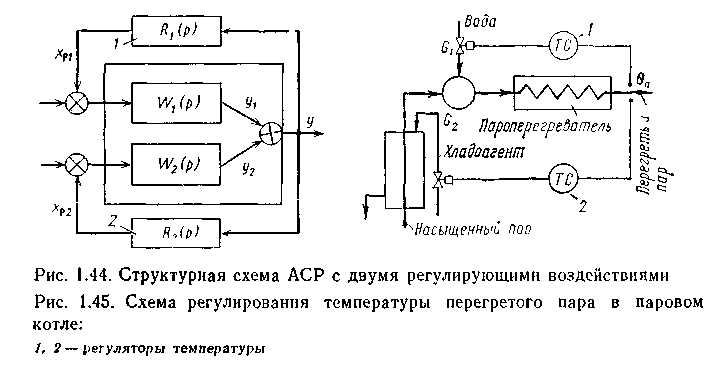
имеющим передаточную функцию W1(p) используют АСР с двумя регулирующими воздействиями — по каналам xp1 и xp2. При этом регулятор 1 должен осуществлять П-закон регулирования, а регулятор 2 — ПИ- или ПИД-закон. Задача регулятора 2 состоит в ликвидации статической ошибки регулирования. При этом y(°°)=0 и, следовательно, равно нулю регулирующее воздействие xp1. Регулятор 1 настраивают по характеристикам объекта с передаточной функцией W1(p), а регулятор 2 — по характеристике эквивалентного объекта W0(p). Чтобы получить эту характеристику, нужно учесть, что
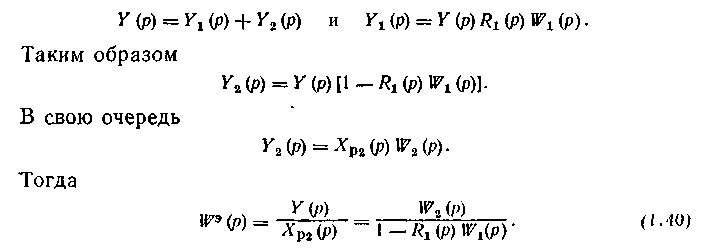
Примером системы с двумя регулирующими воздействиями может служить система регулирования температуры перегретого пара в паровом котле (рис. 1.45). Регулятор 1 меняет расход воды, впрыскиваемой в коллектор пароохладителя. Однако в статическом режиме расход воды g1 должен быть минимальным. Регулятор 2 меняет расход хладоагента G2 через поверхностный теплообменник. Как будет показано в разделе 2.3, динамика объекта но каналу G2—Qп значительно хуже, чем по каналу gi—QП, по экономичность регулирования гораздо выше.
62
1.4.2. Регулирование нестационарных объектов
Многие технологические процессы, (в производстве лаков и красок, в микробиологической и пищевой отраслях промышленности), проводят в нестационарных условиях. Для некоторых процессов нестационарность обусловлена изменением характеристик аппарата вследствие изменения его нагрузки, образования накипи на трубах, старения катализатора и т. п. Иногда процессы проводят в нестационарных (обычно циклических) режимах с целью повышения их эффективности [54]. Во всех этих случаях линеаризованная математическая модель процесса нестационарна, а правые части дифференциальных уравнений содержат координату времени в явной форме.
В случае нестационарных процессов предъявляют особые требования к построению систем стабилизации их параметров. Например, в процессах биосинтеза температура должна поддерживаться на заданном оптимальном уровне изменением расхода охлаждающей воды. По мере роста концентрации биомассы вязкость среды растет, а от нее сильно зависят коэффициенты теплопередачи. Таким образом, передаточная функция объекта регулирования температуры в начале и в конце процесса существенно различны. Систему регулирования необходимо рассчитать таким образом, чтобы обеспечить удовлетворительное качество переходных процессов для всех возможных значений параметров линеаризованной модели. Рассмотрим некоторые особенности построения таких систем. Обеспечение рабастности систем регулирования. Термин «рабастность» означает малую чувствительность систем регулирования к изменению тех или иных свойств управляемого процесса. Обеспечить рабастность можно различными способами. Одним из них является такой выбор настроечных параметров регуляторов, чтобы при некоторых средних характеристиках процесса степень устойчивости замкнутой системы ц (минимальное расстояние корней ее характеристического уравнения от мнимой оси) была максимальна. Поскольку для системы регулирования опасна потеря устойчивости, такой выбор настроек позволяет надеяться на удовлетворительное качество регулирования при колебаниях параметров передаточной функции объекта.
Другим способом обеспечения рабастности — более надежным, по и более трудоемким — является выбор настроек регуляторов, оптимальных по отношению к наиболее неблагоприятному сочетанию параметров процесса. Если процесс можно приближенно охарактеризовать передаточной функцией апериодического или нейтрального объекта с запаздыванием, то, зная диапазон изменения коэффициента усиления, постоянной времени и времени запаздывания, можно выбрать такое сочетание этих параметров, для которого оценка среднеквадратичной ошибки регулирования максимальна.
63
Для астатического объекта с передаточной функцией
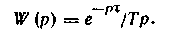
наиболее неблагоприятному сочетанию параметров соответствует максимальное отношение т/Т
Для статическою объекта с передаточной функцией
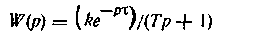
и П-регулятора наихудшее качество регулирования соответствует максимуму выражения
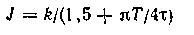
на множестве возможных значений k, l, т Именно для тех параметров, при которых / максимально, нужно выбирать настройки регуляторов
Аналогичный подход полезен не только для нестационарных процессов, но и при назначении параметров регуляторов априори для целого класса объектов, характеристики которых сравнительно мало отличаются друг от друга.
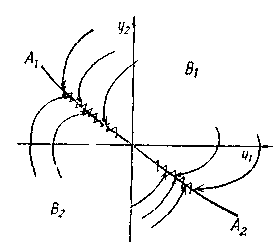
Для объектов без существенного запаздывания рабастность можно обеспечить выбором регуляторов с переменной структурой [21] Такие регуляторы позволяют создать переходный процесс в замкнутой системе, близкий к некоторому желаемому, путем введения так называемою скользящею режима. При переходе фазовой траектории системы через границу, совпадающую с фазовой траекторией желаемой системы, коэффициенты регулятора меняются, при этом возникает движение вдоль границы с постоянно изменяющимися параметрами регулятора (рис. 1.4G). При изменении свойств объекта меняются только такие характеристики скользящего режима, как частота переключении. Основная же траектория, вдоль которой проходит скользящее движение, остается неизменной. Использование параметрической компенсации. Изложенные выше подходы к регулированию нестационарных процессов предполагали, что характеристики регулятора не меняются, несмотря па изменение свойств объекта Между тем, если возмущение, меняющее динамику объекта, можно измерить, то

естественно использование принципа параметрической компенсации. При этом параметры регулятора изменяют таким образом, чтобы, несмотря на изменение динамики объекта, степень устойчивости или степень колебательности системы
64
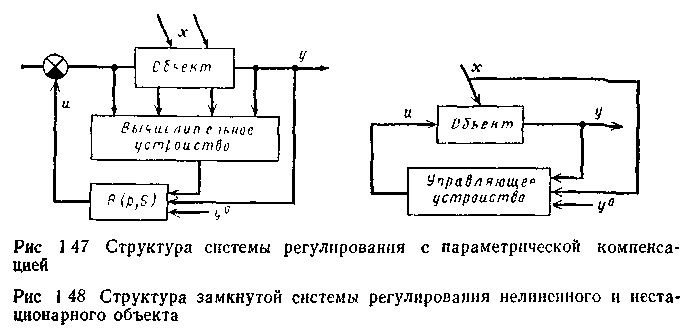
не менялись Чаще всего таким измеряемым параметрическим возмущением является нагрузка объекта (расход материальных и энергетических потоков) Через контур адаптации изменение нагрузки меняет параметры регулятора таким образом, чтобы коэффициент усиления разомкнутой системы остался неизменным (рис 1 47).
Синтез системы управления из условия заданного характера переходного процесса в замкнутой системе. В замкнутой системе регулирования, показанной на рис. 1.48, объект и управляющее устройство нелинейны. Уравнение, характеризующее объект, имеет вид.
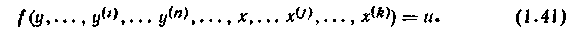
Здесь y(i),x(j) — i-тая и j-тая производные регулируемой координаты у и возмущающего воздействия х. Требуемые динамические свойства замкнутой системы можно охарактеризовать дифференциальным уравнением, связывающим задающее воздействие у0 с выходом объекта у, вектором возмущений х и вектором параметров регулятора S:
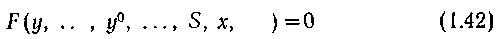
Представленная в виде (1.42) функция F может содержать не только переменные у, х, у°, но и их производные. В частности, в условие (1,42) обязательно должна входить высшая ' производная у(n), причем так, чтобы это условие можно было разрешить относительно нее.
Закон изменения управления и выбирают из условия, чтобы
фактическое изменение у в замкнутой системе совпадало с же-
лаемым [8], для этого должны совпадать и их производные.
Обозначим желаемый закон изменения координаты // через у
Высшую производную желаемого движения находят, разрешив

и потребуем выполнения равенства
65
уравнение (1.42) для желаемой системы относительно y(n):

Управление, обеспечивающее выполнение равенства (1.43), можно найти, подставив в уравнение объекта (1, 41) вместо производном y(n) ее желаемое значение. Получим
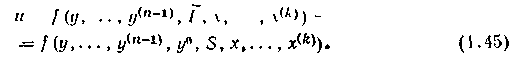
При этом управление становится функцией переменных у, .., У(п-1), ..., х, .., x(k\ S, y°, ..., y(n-1)0. Все эти переменные рассматривают как измеряемые В этом случае получают алгоритм управления в форме синтеза. Далеко не всегда производные выходной координаты (а также возмущающие воздействия и их производные) можно измерить; однако при невысоком порядке объекта подобный подход оказывается эффективным, а зачастую позволяет найти удовлетворительный приближенный алгоритм управления, не использующий измеренных значений всех переменных, входящих в уравнение (1.45). Методика использования изложенного подхода показана ниже па примере.
Пример. Управление реактором идеального смешения. Уравнение, характеризующее динамику изотермического реактора смешения, имеет вид
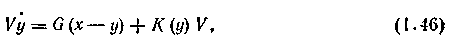
где у — концентрация в объеме аппарата и на выходе его; х — концентрация во входном потоке; G и V — соответственно расход через реактор и объем реактора, К(у) —скорость реакции, зависящая от концентрации
Пусть управляющим воздействием является расход G через аппарат. Уравнение (1.46) нелинейно, так как в него входят нелинейная функция К(y) и произведение G(x—у) Зададим характер желаемого переходного процесса в замкнутой системе уравнением
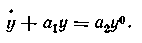
Таким образом, для выработки управления необходимо вводить в вычислительное устройство все переменные, фигурирующие в правой части равен-
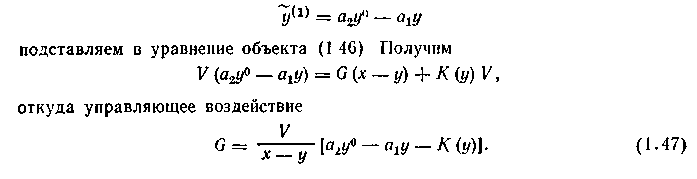
Согласно этому уравнению, желаемый переходный процесс представляет собой экспоненту, имеющую декремент затухания at и стремящуюся к значению a2y0/a1 .Отметим, что порядок высшей производной как в уравнении объекта, так и в уравнении желаемой системы одинаков, что является необходимым условием применимости изложенного подхода Желаемое значение высшей производной
66
ства (1 47), знать уравнение кинетики процесса, т е функцию К(у) При этом объект может быть и нестационарным, например рабочий объем V может медленно меняться, функция К(У) может содержать зависящие от времени коэффициенты и т. д Если же скорость изменения V соизмерима
с у, это надо учесть при записи уравнения (1 47), что приведет к изменению закона управления, синтезированного с помощью изложенного подхода
На первым взгляд, желаемое уравнение системы можно задать произвольно, и найденный закон управления обеспечит сколь угодно высокое качество переходных процессов. Подобное представление создается вследствие того, что при синтезе не учитывались ограничения на множество возможных значений управления. Так, в примере с химическим реактором G не может быть отрицательным и не может превышать некоторого предельного значения. Эти ограничения можно учесть путем выбора а1 и а2 в желаемом уравнении с учетом диапазона изменения х и у°
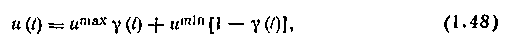
В ряде случаев множество допустимых управлений может состоять из отдельных фиксированных значений и. В этом случае полезно учесть, что для выполнения равенства между фактической и желаемой кривыми изменения у равенство между их высшими производными может быть выполнено лишь в среднем на каждом достаточно малом (по сравнению с длительностью переходного процесса) отрезке времени. Это значит, что управление может меняться, принимая, например, лишь два фиксированных значения, одно из которых больше, а другое меньше рассчитанного по формуле (1.47), по так, чтобы среднее значение совпало с расчетным. Формально это будет означать замену управления и выражением
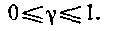
в котором функция y удовлетворяет неравенству Равенство (1.48) нужно подставить в условие (1.45) и разрешить его относительно у. Найденная функция покажет, в течение какого времени в окрестности момента t управляющее воздействие должно принимать максимально возможное значение.
В системах с переменной структурой управляющим воздействием нужно считать параметры регулирующего устройства, которые обычно принимают два значения, переключаясь между ними так, чтобы поведение системы было ближе к желаемому. Такие системы близки к системам, синтезированным на основе изложенного выше подхода. Режим с быстрыми переключениями (скользящий) является для них типовым. Регулирование циклического режима. При циклическом режиме работы переменные, характеризующие состояние процесса, периодически изменяются. Простейшим примером циклического процесса может служить регенеративный теплообмен, когда насадка поочередно контактирует с горячим и холодным потоками, передавая тепло от одного потока к другому.
67
Система регулирования таких процессов должна стабилизи-роваи, фазу и амплитуду колебаний переменных. Регулятор (обычно импульсный) получает информацию периодически с интервалом, равным периоду колебаний, и меняет форму или интенсивность управляющих воздействий, представляющих собой периодические функции
В регенеративном теплообменнике, например, регулируемой величиной является средняя за цикл температура нагреваемого потока. Ее значение поступает на вход регулятора периодически, с интервалом Т0, равным продолжительности цикла. При этом регулятор изменяет средний расход греющего потока.
1.5. ПРЕДВАРИТЕЛЬНЫЙ ВЫБОР СТРУКТУРЫ
И ОЦЕНКА ПАРАМЕТРОВ СИСТЕМЫ РЕГУЛИРОВАНИЯ
При проектировании систем регулирования технологических процессов необходимо выбрать структуру системы и дать предварительную оценку параметров регуляторов. Сведения о динамических свойствах процесса зачастую получают по данным о действующих объектах аналогичного типа или на основе аналитического описания отдельных элементов процесса После того, как система регулирования установлена и технологически ский процесс запущен, параметры регуляторов (а иногда и структуру системы) приходится уточнять.
Выбор структуры АСР и параметров регуляторов целесообразно проводить в такой последовательности
оценить динамические свойства объекта, интенсивность помех и требования к качеству регулирования; все эти сведения являются исходными данными для последующих расчетов;
оценить связи между переменными в статическом режиме, выяснить возможность создания системы регулирования, установить число статически независимых управляющих воздействий и регулируемых параметров;
выбрать параметры регуляторов и оценить качество регулирования для различных законов регулирования в одноконтурных системах;
предварительно выбрать способ улучшения качества регулирования.
Предварительная оценка характеристик процесса регулирования. Характеристики объекта, как правило, нелинейны, однако в системах стабилизации большая часть переменных меняется в сравнительно узкой области. Поэтому будем считать (см.раздел 1.1), что введенные выше вектора у, и, z представляют собой отклонения соответствующих переменных от их средних значений, а характеристики объекта в окрестности заданного номинального режима могут быть линеаризованы. В линейном приближении связи между возмущающими воздействиями z, регулирующими воздействиями и и выходными переменными y
68
можно охарактеризовать, с помощью матриц передаточных функций WВ(p), Wр(p) (см. рис. 1.1).
Так как на этапе предварительного выбора системы регулирования характеристики объекта известны очень приближенно, в подавляющем большинстве случаев динамику процесса можно охарактеризовать одной из двух передаточных функций [42]:

б) передаточной функцией астатическою объекта с запаздыванием
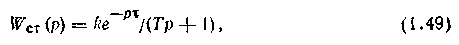
а) передаточной функцией статического объекта первого порядка с запаздыванием
Амплитудно-фазовые характеристики и способы определения параметров этих объектов по их переходным функциям показаны на рис. 1.49. Таким образом, в первом приближении динамические свойства объекта по каждому из каналов могут быть охарактеризованы постоянной времени Т, временем чистого запаздывания т, а для статического объекта — еще и коэффициентом усиления k
Для выбора структуры системы регулирования наряду с динамикой объекта нужно приближенно оценить характеристики возмущающих воздействии В качестве таких характеристик обычно принимают максимальное отклонение Дz или среднеквадратичное отклонение <тг.
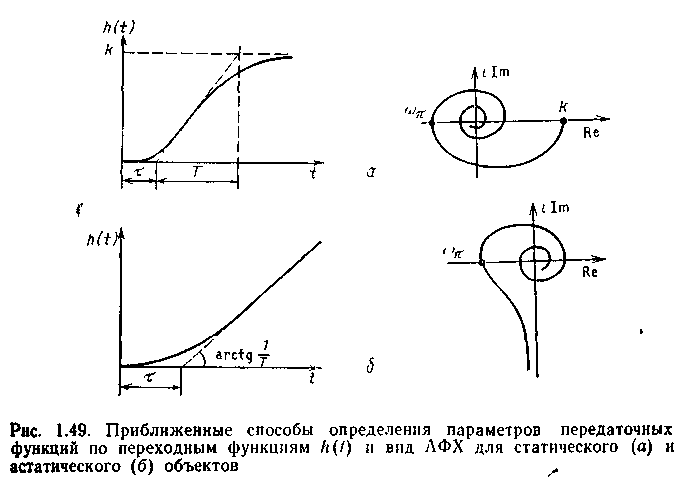
69

Наконец, нужно оцепить необходимую точность стабилизации каждой из составляющих у По тex-нологическим условиям процесса эта точность может быть охарактеризована предельно допустимым отклонением Дy, либо среднеквадратичной ошибкой ау. Если известно только одно из этих значений, второе можно найти из соотношения
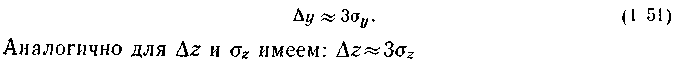
Исходные данные для выбора структуры системы удобно свести в таблицу вида 1.4 (стр. 81), где в первой строке приведены выходные переменные и требования к их точности; в первом столбце приведены управляющие и возмущающие воздействия и их характеристики; во внутренних клетках таблицы записаны параметры, характеризующие динамику объекта по каналу от соответствующего управляющего или возмущающего воздействия к выходной координате.
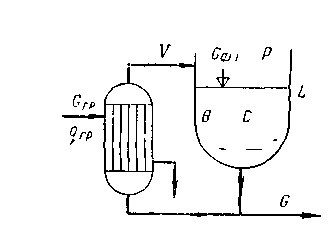
Проиллюстрируем выделение различных групп переменных на примере куба ректификационной колонны с выносным кипятильником (рис. 1.50). Куб колонны представляет собой емкость, заполненную кубовой жидкостью с концентрацией ключевого компонента ск; уровень жидкости L. Жидкость находится при температуре кипения; из выносного теплообменника в колонну поступает паро-жидкостная смесь, сепарируется, и паровой поток подается в верхнюю часть колонны, а жидкость стекает обратно в куб. В свою очередь, из нижней части колонны жидкость отбирается, часть ее направляется в кипятильник, а часть — в сборник готового продукта. Расход жидкости в сборник обозначим G, давление в колонне Р, расход пара в колонну V, расход греющего пара в кипятильник Сгр, энтальпию пара qгр, поток флегмы из верхней част колонны в куб
Gфл.
Выходными переменными являются концентрация и температура в кубе, а также уровень L; управляющими воздействиями могут быть расход греющего пара в кипятильник и расход целевого продукта G. Возмущениями являются расход флегмы, давление в колонне, энтальпия греющего пара. При этом по емкости куба и номинальным значениям расходов потоков можно оценить постоянные времени; по статическим зависимостям, в частности по кривым равновесия, связывающим концентрацию и температуру в статическом режиме, можно найти коэффициенты усиления. Динамические свойства кипятильника можно оценить по результатам анализа подобных аппаратов
