У (к = 1,2,…). Однако на практике часто выгоднее выражать значения производных не через конечные разности, а непосредственно через значения функции в узлах

Вид материала

Лекция

Содержание Обратим внимание 3 узла интерполяции ( Метод неопределенных коэффициентов Пример: Найти выражение для производной у1в случае четырех равностоящих узлов (n = 3) Решение Уточнение аппроксимации Частные производные Определенным интегралом Теорема о существовании определенного интеграла

Подобный материал:

• В. И. Афанасьева 01 марта 2011 г. Программа, 116.92kb.
• I. Мгновенный ток называется периодическим, если значения его повторяются через одинаковые, 47.27kb.
• Курсовая работа по информатике, 20.84kb.
• Отсчет по курсовой работе на тему: нахождение корней уравнений методом хорд, 32.38kb.
• Мониторинг средств массовой информации за 18-19, 424.03kb.
• Конституцией Российской Федерации, федеральными закон, 631.34kb.
• «Чойский район», 375.55kb.
• В новосибирской области, 662.53kb.
• Диффузия в биологических системах. Диффузия, 145.79kb.
• Рф самостоятельная и под свою ответственность деятельность нас-я по решению непосредственно, 1382.37kb.

Лекция 13

Интерполяционные многочлены Ньютона дают выражения для производных через разности Δ^к у (к = 1,2,…). Однако на практике часто выгоднее выражать значения производных не через конечные разности, а непосредственно через значения функции в узлах. Для получения таких формул удобно использовать формулу Лагранже с равномерным расположением узлов (х_{i –} x_i-1 = h = const; i=1,2,…,n).

Запишем интерполяционный многочлен Лагранже и его остаточный член для случая трех узлов интерполяции (n = 2) и найдем их производные:

Z(x) = 1/2h² [(x – x₁)(x – x₂)y₀ – 2(x – x₀)(x – x₂)y₁ + (x – x₀)(x – x₁)y₂]

R_z(x) = y_*'''/3!(x - x₀)(x – x₁)(x – x₂)

Z'(x) = 1/2h² [(2x – x₁ – x₂)y₀ – 2(2x – x₀ –x₂)y₁ + (2x – x₀ – x₁)y₂]

R'_z(x) = y_*'''/3! [(x – x₁)(x – x₂) + (x – x₀)(x – x₂) + (x –x₀)(x – x₁)]


y_*^''' – значение производной третьего порядка в некоторой точке х_* є [x₀, x_n]


Запишем выражение для производной у₀' при х = х₀:

у₀' = Z' (x₀) + R_z' (x₀) = 1/2h² [(2x₀ – x₁ – x₂)y₀ – 2(2x₀ – x₀ – x₂)y₁ + (2x₀ – x₀ – x₁)y₂] +

+ y_*'''/3![(x₀ – x₁)(x₀ – x₂) + (x₀ – x₀)(x₀ – x₂) + (x₀ – x₀) (x₀ – x₁)] = 1/2h(-3y₀ + 4y₁ – y₂) + h²/3 y_*'''

Аналогичные выражения можно получить для значений y₁' при х = х₂; у₂' при х = х₂:

y₁' = 1/2h (y_{2 –} y₀) – h²/6 y_*'''

y₂' = 1/2h (y₀ – 4 y₁ + 3 y₂) + h²/3 y_*'''


Для каждой из этих формул y_*''', вообще говоря различны.


Для случая четырех узлов (n = 3) получим следующие аппроксимации производных:

у₀' = 1/6h (-11у₀ +18у₁ – 9у₂ + 2у₃) – h³/4 у_*^'v

у₁^' = 1/6h (-2у₀ – 3у₁ + 6у₂ – у₃) + h³/12 у_*^'v

у₂^' = 1/6h (у₀ – 6у₁ +3у₂ + 2у₃) - h³/12 у_*^'v

у₃^' = 1/6h (-2у₀ + 9у₂ + 11у₃) + h³/4 у_*^'v


Таким образом, используя значения функции в n + 1 узле, получаем аппроксимацию производных n-го порядка. Эти формулы можно использовать для любых узлов х = х_i, x_i+1,…, меняя значения индексов соответствующим образом.

^ Обратим внимание: при четных n наиболее простые выражения и наименьшие коэффициенты в остальных членах получаются для производных в средних (центральных узлах):

у₁^' при n = 2; y₂^' при n = 4 и т.д.

Аппроксимации производных для узла с произвольным номером i, считая его центральным:

у_i^' = 1/2h (y_i+1 – y_i-1) – h²/6 y_*''' , n = 2 (13.1)

y_i' = 1/12h (y_i-2 – 8y_i-1 + 8y_i+1 – y_i+2) + h⁴/30 у_*^'v , n=4

Они называются – аппроксимации производных с помощью центральных разностей.

Это в точности есть аппроксимация (12.12)

Широко используются на практике.

С помощью интерполяционных многочленов Лагранже можно получить аппроксимации для старших производных. Например, для двух производных:

^ 3 узла интерполяции (n = 2):

y₀^'' = 1/h² (y₀ – 2y₁ + y₂) + O(h) O(h) – погрешность аппроксимации;

y₁^'' = 1/h² (y₀ – 2y₁ + y₂) + O(h²) зависит от шага h; предполагают, что

y₂^'' = 1/h² (y₀ – 2y₁ + y₂) + O(h) ׀h׀ < 1


Подробнее о погрешности аппроксимации можно посмотреть Турчак стр. 74-75.


4 узла (n=3):

y₀^'' = 1/h² (2y₀ – 5y₁ + 4y₂ – y₃) + O(h²)

y₁^'' = 1/h² (y₀ – 2y₁ + y₂) + O(h²)

y₂^'' = 1/h² (y₁ – 2y₂ + y₃) + O(h²)

y₃'' = 1/h² (-y₀ – 4y₁ – 5y₂ + 2y₃) + O(h²)


5 узлов (n = 4):

y₀^'' = 1/12h² (35y₀ – 104y₁ + 144y₂ – 56y₃ + 11y₄) + O(h³)

y₁^'' = 1/12h² (11y₀ – 20y₁ + 6y₂ +4y₃ – y₄) + O(h³)

y₂^'' = 1/12h² (-y₀ + 16y₁ – 30y₂ + 16y₃ – y₄) + O(h³)

y₃^'' = 1/12h² (-y₀ + 4y₁ + 6y₂ – 20y₃ + 11y₄) + O(h³)

y₄^'' = 1/12h² (11y₀ – 56y₁ + 114y₂ – 104y₃ + 35y₄) + O(h³)


Аппроксимации вторых производных с помощью центральных разностей при четных n так же наиболее выгодны.


^ Метод неопределенных коэффициентов

Для случая произвольного расположения узлов можно получить аналогичные формулы. Использование многочлена Лагранжа в этом случае приводит к вычислению громоздких выражений, поэтому удобнее применять метод неопределенных коэффициентов. Он заключается в следующем: искомое выражение для производной к-го порядка в некоторой точке х = х_i представляется в виде линейной комбинации заданных значений функции в узлах х₀, х₁,…, х_n:

y_i^(k) ≈ C_oy₀ + C₁y₁ + … + C_ny_n (13.2)


Предполагаем, что это соотношение выполняется точно, если функция у м.б. представлена в виде многочлена степени не выше n:

y = b₀ + b₁(x – x₀) + … b_n(x – x₀)ⁿ


Отсюда следует, что соотношение (13.2) должно выполняться точно и для многочленов:

у =1;

у = х – х₀;

у = (х – х₀)ⁿ

Последовательно подставляя эти выражения в (13.2) и требуя выполнения точного равенства, получаем систему n + 1 линейных уравнений для определения неизвестных коэффициентов С₀, С₁,…, С_n.

^ Пример: Найти выражение для производной у₁^' в случае четырех равностоящих узлов (n = 3)

Решение: Запишем приближенно производную в виде

у₁^' ≈ С₀у₀ + С₁у₁ + С₂у₂ + С₃у₃ (13.3)

Используем следующие многочлены:

у =1; у = х – х₀; у = (х – х₀)²; у = (х – х₀)³

Вычислим их производные:

y^' = 0; y^' = 1; y^' = 2(х – х₀); y^' = 3(х – х₀)²

Подставляем последовательно эти соотношения в левую и правую части искомой формулы при х = х₁, требуя выполнения точного равенства:

0 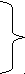= С₀1 + С₁1 + С₂1 + С₃1

1 = С₀(х₀ – х₀) + С₁(х₁ - х₀) + С₂(х₂ – х₀) + С₃(х₃ – х₀)

2(х₁ - х₀) = С₀(х₀ – х₀)² + С₁(х₁ - х₀)² + С₂(х₂ – х₀)² + С₃(х₃ – х₀)²

3(х₁ - х₀)² = С₀(х₀ – х₀)³ + С₁(х₁ - х₀)³ + С₂(х₂ – х₀)³ + С₃(х₃ – х₀)³


Получаем систему уравнений:

С₀ + С₁ + С₂ + С₃ = 0 Решая эту систему,

hС₁ + 2hС₂ + 3hС₃ = 1 получим: С₀ = -1/3h; С₁ = -1/2h;

hС₁ + 4hС₂ + 9hС₃ = 2 С₂ = 1/h; С₃ = - 1/6h;

hС₁ + 8hС₂ + 27hС₃ = 3


Подставляя эти значения в (13.3), получим:

у₁^' ≈ 1/6h (-2у₀ – 3у₁ + 6у₂ – у₃)


^ Уточнение аппроксимации

Из конечно – разностных соотношений для аппроксимации производных видно, что порядок их точности возрастает с увеличением числа узлов аппроксимации. НО!

При большом числе узлов эти соотношения становятся весьма громоздкими, что ведет к существенному возрастанию объема вычислений. Усложняется оценка точности получаемых результатов.

Существует простой и эффективный способ уточнения решения при фиксированном числе узлов, используемых в аппроксимирующих конечно-разностных соотношениях. Он называется методом Рунге-Ромберга.

Суть метода:

Пусть F(x) – производная, которая подлежит аппроксимации; f(x,h) – конечно-разностная аппроксимация этой производной на равномерной сетке с шагом h; R – погрешность (остаточный член) аппроксимации, которую запишем в виде:

R= h^p φ (x) + O (h^p+1)

Тогда выражение для аппроксимации производной в общем случае можно представить в виде:

F(x) = f(x, h) + h^p φ(x) + O(h^p+1) (13.4)

Запишем это соотношение в той же точке х при другом шаге h₁ = kh:

F(x) = f(x, kh) + (kh)^p φ(x) + O((kh)^p+1) (13.5)

Приравнивая правые части равенств 13.4 и 13.5, получим выражение для главного члена погрешности аппроксимации производной:



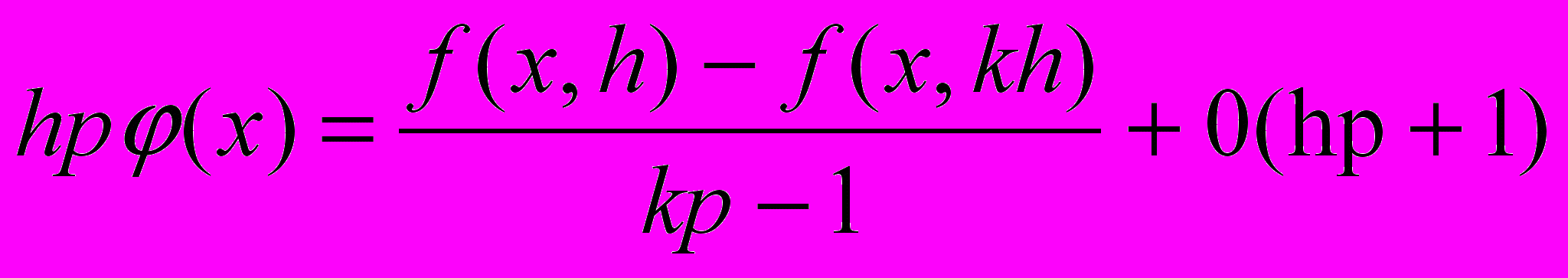
Подставляем в 13.4:

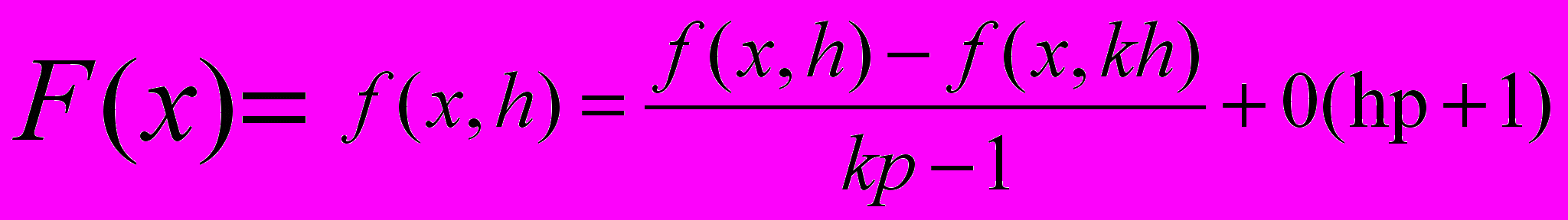– формула Рунге (13.6)

Эта формула позволяет по результатам двух расчетов значений производной f(x, h) и f(x, kh) (с шагами h и kh) с порядком точности р найти ее уточненное значение с порядком точности р+1.

Пример: Вычислить производную функции y = x³ в точке x = 1.

Очевидно: y' = 3x²

y'(1) = 3

Найдем теперь эту производную численно.

Составим таблицу значений функции

х	0,8	0,9	1,0
у	0,512	0,729	1,0

Воспользуемся аппроксимацией производной с помощью левых разностей, имеющей первый порядок (р = 1).

Примем шаг равным 0,1 и 0,2, т.е. к = 2

Получим:

f(x,h) = y'(1;0,1)



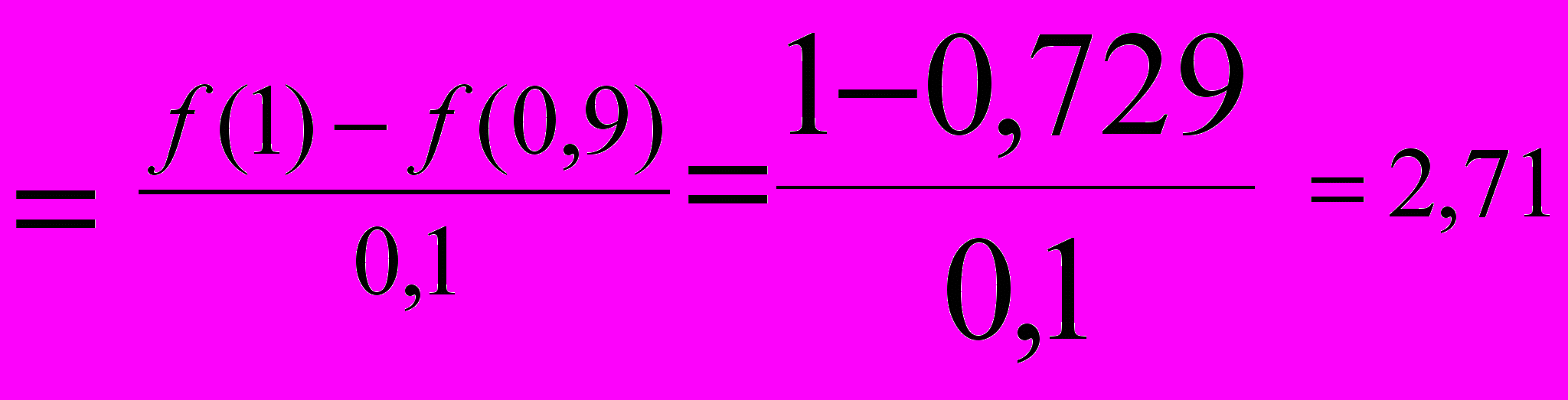
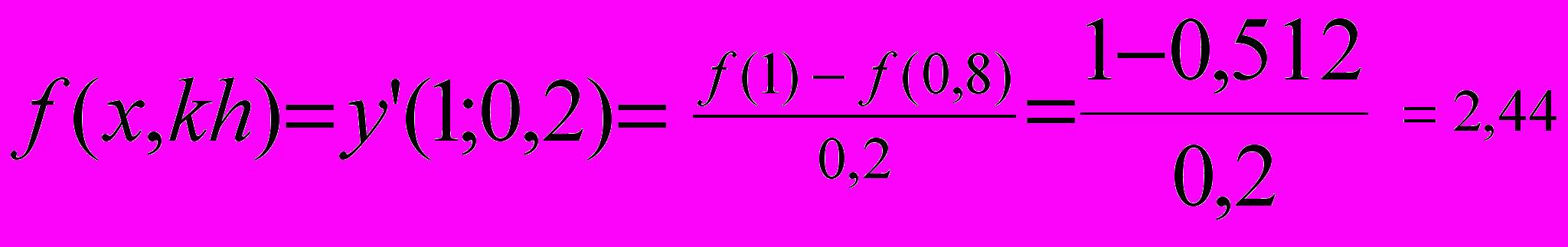
по формуле Рунге найдем уточненное значение производной:



Т. о., формула Рунге дает более точное значение производной. В общем случае порядок точности аппроксимации возрастает на единицу. Мы рассмотрим уточнение решения, полученного при двух значениях шага. Теперь предположим, что расчеты могут быть проведены с шагами h_1, h₂,…, h_g. Тогда можно получить уточненное решение для производной F(x) по формуле Ромберга:



F(x,h₁) h₁^p h₁^p+1 … h₁^p+q-2

f(x,h₂) h₂^p h₂^p+1 … h₂^p+q-2

..................................................

F(x,h_g) h_g^p h_g^p+1 … h_g^p+q-2

F(x) = + 0(h^p+g-1) (13.7)

1 h₁^p h₁^p+1 … h₁^p+q-2

1 h₂^p h₂^p+1 … h₂^p+q-2

1 h_g^p h_g^p+1 … h_g^p+q-2


Порядок точности, т.о., возрастает на g – 1.

Важно: для успешного применения уточнения исходная функция должна иметь непрерывные производные достаточно высокого порядка.


^ Частные производные

Смотреть Турчак стр. 82-85


Численное интегрирование

Вспомним некоторые понятия.

Пусть на [a,b] задана функция у = f(x). С помощью точек х_0, х₁,…, х_n разобьем [a,b] на n элементарных отрезков [x_i-1,x_i] (i = 1,…,n).

x₀ = a, x_n = b.

На любых из этих отрезков выберем произвольную точку E_i(x_i-1 ≤ ٤_i ≤ x_i)

Найдем произведение S_i = f(٤_i) Δx_i (13.8)

f(٤_i) – значение функции в этой точке, Δx_i = x_i – x_i-1 – длина элементарного [ ]

Составим сумму всех таких произведений:

S_n = ζ₁ + ζ₂ + … + ζ_n = ∑_i=1ⁿ f(٤_i) Δx_i (13.9)

Сумма S_n называется интегральной суммой.

^ Определенным интегралом от функции f(x) на [a,b] называется предел интегральной суммы при таком неограниченном увеличении числа точек разбиения, при котором длина наибольшего из элементарных отрезков стремится к пустому множеству:

∫ f(x)dx = lim_maxΔxi→0 ∑_i=1ⁿ f(ξ_i) Δx_i (13.10)


^ Теорема о существовании определенного интеграла:

Если функция f(x) непрерывна на [a,b], то предел интегральной суммы существует и не зависит ни от способа разбиения [a,b] на элементарные отрезки, ни от выбора точек ξ_i


Геометрический смысл рассмотрим для случая f(x) > 0.

Абсциссами точек М_i являются значения ξ_i, ординатами - значения f(ξ_i).


Выражения для ζ_i (13.8) при I = 1,2…,n описывает площади элементарных прямоугольников; интегральная сумма S_n (13.9.) – площадь ступенчатой фигуры, образуемой этими прямоугольниками. При неограниченном возрастании числа точек деления и стремлении к пустому множеству всех элементов Δx_i верхняя граница фигуры (ломанная) переходит в линию y = f(x). Площадь полученной криволинейной трапеции равна определенному ∫ (13.10).

Во многих случаях, когда подынтегральная формула задана в аналитическом виде, определенный интеграл удается вычислить непосредственно с помощью первообразной по формуле Ньютона-Лейбница: определенный интеграл равен приращению первообразной F(x) на отрезке интегрирования:

∫_a^b f(x) dx = F(x)│_a^b = F(b) – F(a) (13.11)

Однако на практике этой формулы часто нельзя воспользоваться по двум причинам:

1. вид функции f(x) не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях;
   
2. значения функции f(x) заданы только на фиксированном конечном множестве точек х_i, т.е. функция задана в виде таблицы.
   

В этих случаях используются приближенные методы интегрирования. Они основаны на аппроксимации подынтегральной функции некоторыми более простыми выражениями, например: многочленами.

Одним из таких способов для первого случая, является представление подынтегральной функции в виде степенного ряда (ряда Тейлора). Это позволяет свести вычисление интеграла от сложной функции к интегрированию многочлена, представляющего первые несколько членов ряда.

Пример: Вычислить I = ∫₀¹ e^-x2 dx

с погрешностью 10^-4

Разложим экспоненту в ряд:

е^x = 1 + x + x²/2! + x³/3! + …

Заменим х на –х².

Интеграл запишется в виде:

I = ∫₀¹ (1 – x² + x⁴/2! – x⁶/3! + …) dx = x – x³/3 + x⁵/5*2! – x⁷/7*3! + … │₀¹ = 1 – 1/3 + 1/10 – 1/42 + … ≈ 0,7468

Более универсальными методами, которые пригодны для обоих случаев, являются методы численного интегрирования, основанные на аппроксимации подынтегральной функции с помощью интерполяционных многочленов. Такая аппроксимация позволяет приближенно заменить определенный ∫ конечной суммой

∫_a^b f(x) dx ≈ ∑_i=0ⁿ a_i y_i (13.2)

где у_i – значения функции в узлах интерп-ции, λ_i – числовые коэффициенты.

Формулы (13.12) называется квадратной формулой, правая часть этого соотношения называется квадратной суммой.

В зависимости от способа ее вычисления получаются разные методы численного интегрирования – методы прямоугольников, трапеций, парабол, сплайнов и др.

К вычислению определенного ∫ сводятся многие практические задачи: вычисление площади фигур, определение работы переменной силы и т.д.