Если использовать разности высших порядков вплоть до n-го, то разностное уравнение 1
| Вид материала | Документы |
- Частные производные и дифференциалы высших порядков п. Частные производные высших порядков, 190.6kb.
- Статья Тема: «Уравнения высших степеней с параметрами», 55.64kb.
- § Тема. Некоторые определения и обозначения, 1005.59kb.
- Статьи на русском, 122.97kb.
- Решение кубического уравнение в общем виде. От общего кубического уравнения к упрощённому, 14.77kb.
- У (к = 1,2,…). Однако на практике часто выгоднее выражать значения производных не через, 96.45kb.
- Содержание уравнения математической физики (нм-3) Уравнения математической физики (нп-3), 92.05kb.
- Определители 2-го и 3-го порядков: определения и применение к решению систем линейных, 42kb.
- Диффузия в биологических системах. Диффузия, 145.79kb.
- Методические рекомендации студентам, 215.81kb.
80

Пример. Проиллюстрируем последовательность применения изложенной методики на примере выбора системы регулирования для колонны ректификации смеси метанол — вода [43] Схема колонны показана на рис 1,55 Регулируемыми величинами являются мольные концентрации метанола в дистилляте и кубовой жидкости i/i и t/2, а также уровни жидкости в кубе и в дефлегматоре Контуры регулирования уровней можно рассматривать в первом нрибипжсшш независимо от концентрации Будем полагать [43J, что регулирование уровня и дефлекторе осуществляется изменением расхода верхнею продукта, а в кубе — нижнего Да не будем рассматривать только регулирование состава Управляющими воздействиями являются поток пара на входе в кипятильник и2 и поток флегмы, направляющийся в колонну Ц|, возмущением—поток разделяемой смеси
Характеристики динамики колонны и требования к качеству регулирования можно свести в таблицу (табл 1 4)
Определитель матрицы коэффициентов усиления
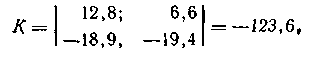
т е не равен нулю, и следовательно, объект статически управляем
Максимальные отклонения у\ и уг в статическом режиме при отсутствии регуляторов равны

Таким образом, установка регуляторов необходима
Расчет настроек регуляторов по приближенным формулам габч 12 дает следующие значения

81
Для приведения возмущающих воздействий ко входу каждого из каналов регулирования нужно учесть, что возмущение, приведенное к входу. складывается из влияния возмущения z и воздействия второго контура регулирования по перекрестному каналу, аналогично — для возмущения контура регулирования j/2 Поэтому, строго говоря, нужно решить совместно си стему уравнении
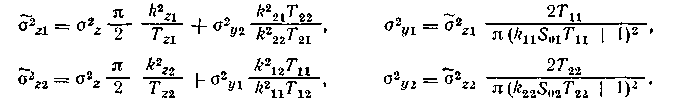
относитечьно 0S1 и аВ2 В этих уравнениях 02г( •—эквивалентные дисперсии возмущении, приведенных к выходу соответствующего канала регулирования Однако при первом просчете можно упростить задачу, заменив в уравнени ях для аг, дисперсии a2ui и а2д2 их максимально допустимыми значениями Расчет при таком допущении приводит к следующим значениям 0г р oVI|l = = 0,16 и аг"р = 0,13 при выборе и\ для peгулирования i/i и U2 — для регулирования г/2, 0z"p=0,12, агпр=0,34 при выборе и\ для регулирования у2 к ы2—для регулирования у, (первыми указаны приведенные ко входу канала регулирования у\ среднеквадратичные значения возмущений)
Подсчитав оценки качества регулирования для П-регулятора сведем их в таблицу вида

Из расчетов следует, что концентрацию кубового остатка у г нелыя регулировать с использованием П регулятора ни по одному из каналов При использовании для регулирования уг ПИ-регулятора по каналу и\ получим а>1, а по каналу u2—ct=0,78 Таким образом, простейшей схемой регулирования колонны разделения смеси метанол — вода является схема с использованием П регулятора (меняющего расход флегмы для поддержания концентрации дистиллята), ПИ-регулятора (меняющего расход пара в куб для поддержания концентрации в нем) При повышении требовании к качеству регулирования эту схему придется усложнить
1.6. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ И ПРОГНОЗИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ СОСТОЯНИЯ ОБЪЕКТА
Один из способов формирования требуемого управляющего воздействия— синтез такой линейной системы (формирующего устройства), реакция которой на заданный входной сигнал совпадает с желаемым сигналом m(t) или мало от него отличается. Способ решения такой задачи позволяет понять существо методов оптимальной фильтрации и прогнозирования стационарных случайных процессов.
Обозначим импульсную характеристику формирующего yci-ройства w(t). Для физически реализуемой системы эта характеристика удовлетворяет требованию
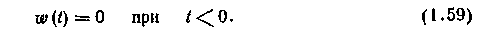
82

Первоначально предположим, что сигналом на входе формирующего устройства является б-функция Тогда его выходом является характеристика w(t); она должна минимизировать квадратичное отклонение
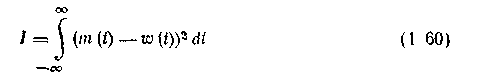
Если функция m(t) равна нулю при /<0, то решение задачи очевидно: w*(t)=tn(t).
Если m(t) отлична от нуля при t
Таким образом, во временной области решение задачи оче видно Несколько сложнее решить ее, если условия заданы в частотной области Например, задано преобразование по Фурье М(1ы) функции m(t) и требуется найти амплитудно-фазовую частотную характеристику IF ((со) формирующего устройства. Для определения W* (ка) нужно представить M(to)) в виде суммы двух слагаемых:

Первому слагаемому соответствует оригинал m+(t), равный нулю при отрицательных значениях t, а второму — при положительных. Разложение (1 61) называют расщеплением. Равенство w(t)=m+(l) в частотной области запишется следующим образом.

Если функция М(иа) дробно рациональная, то разложение (1 61) можно выполнять, не переходя к оригиналам, а воспользовавшись тем, чю для функции /(/), равной нулю при t<.Q и стремящейся к нулю при /->-<», преобразование Лапласа F(p) имеет все полюсы в левой полуплоскости комплексного переменного Наоборот, функция, равная нулю при £>0, имеет преобразование Лапласа с полюсами в правой полуплоскости
Пример. Псть
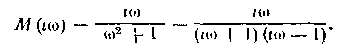
83
Преобразование Лапласа получим из преобразования Фурье заменой ко па р
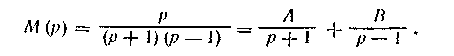
В первом из этих слагаемых полюс р° = — 1,так что это М)во втором понос равен +1, это М- Коэффициенты А и В опредспнм, приведя последнее равенство к общему знаменателю и учитывая, что числитель полученною выражения должен равняться р
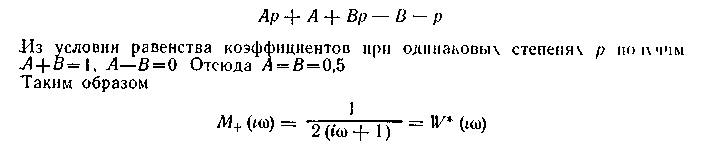
Обобщим задачу синтеза формирующего устройства, предполагая, что на его вход подается сигнал g(t) и требуется так подобрать импульсную характеристику w(t), чтобы выход устройства у(1) минимально отличался от желаемою сигнала m(t)
Если g(t)=0 при <0, задача сводится к предыдущей, так как при t<0 y(t)=0; при >0 нужно сформировать y(t) равным m+(t). В частотной области
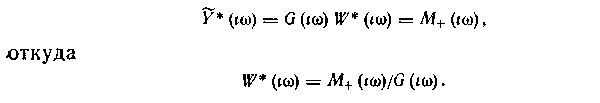
Если g(t)=0 при /<0, поступим следующим образом Отбросим условие физической реализуемости и запишем в частотной области условие равенства желаемого сигнала и сигнала на выходе формирующего устройства:

Преобразуем это равенство к такой форме, чтобы оригинал слагаемого, зависящего от W (/со), обращался в нуль при /*<0. Для этого представим G(ito) в виде
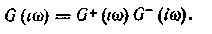
Здесь первому сомножителю соответствует оригинал, равный нулю при £<0, второму — при />0 Такое представление называют факторизацией. Поделим обе части равенства (1.63) на g-(ico). Получим:
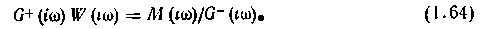
Согласно условию физической реализуемости, оригинал функции W(i(») и, следовательно, произведения G1 (*ш) W(iw), должен обращаться в нуль при <0, при /0 выбором W(tco) можем добиться равенства функций времени, соответствующих левой и правой частям выражения (1 64). Таким образом, наи-
84

лучшему выбору соответствует условие
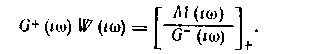
Индекс «плюс» в нижней части квадратной скобки соответствует расщеплению дроби М/G- на два слагаемых:
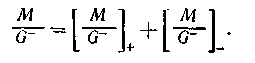
Оригинал первого равен нулю при t<0, второго — при t>0 Окончательно получим.
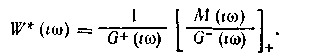
Таким образом, учет требований физической реализуемости формирующего устройства осуществляют в частотой области с помощью двух операций — факторизации и расщепления. Факторизацию используют для того, чтобы множителем при W(i(u) оказалась функция, которой во временной области соответствует оригинал, равный нулю при /<0. Операция расщепления соответствует во временной области разбиению оригинала на два слагаемых, одно из которых определено для tO, другое — для /<0
При этом частотная характеристика оператора связи далеко не
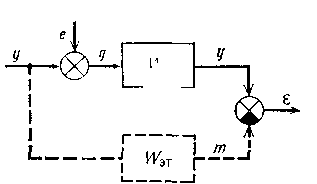
Оптимальная фильтрация и прогнозирование случайных процессов. Пусть на вход линейной системы (фильтра) подается случайный сигнал g(t), равный сумме полезного сигнала y(t) и помехи е(1). Для y(t) и e(t) известно, что это случайные стационарные процессы со спектральными плотностями Sy (со) и 5е(со). Требуется найти такую характеристику фильтра W(ico), чтобы сигнал y(t) на его выходе минимально в среднеквадратичном смысле отличался от желаемого сигнала (рис 1.57). В свою очередь, желаемый сигнал тем или иным способом связан с полезным сигналом. Если, например, m(l)=y(t), 10 задача фильтра заключается в выделении сигнала из ею смеси с помехой. Если m(l)=dyldt, фильтр реализует помехоустойчивое дифференцирование у(1) Если tn(t) = y(t+t), осуществляется помехоустойчивым прогноз полезного сигнала В общем случае связь между у(1) и ///(/) удобно задать в частотной области в виде
85
всегда физически реализуема. Для задачи выделения полезного сигнала Ww(io)) = l; для задачи дифференцирования №Эт(1со) =1ш; для задачи прогноза И?эт(йо) =е'мг Физически реализуема характеристика эталонного оператора только в первом из этих трех примеров.
Критерием оптимальности поставленной задачи является среднеквадратичная величина ошибки р между желаемым сигналом и сигналом у на выходе фильтра Обозначая для краткости кости чертой операцию усреднения, запишем:
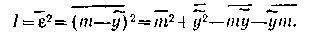
В частотной области среднеквадратичная ошибка запишется в форме

Здесь Se(co)—спектральная плотность ошибки, которая выражается через спектральную плотность сигнала g(t) на входе фильтра, его частотную характеристику и взаимную спектральную плотность входного и желаемого сигналов:

При этом требование физической реализуемости фильтра никак не учитывалось. Произведение 56(ю) W(ia>) равно, как известно, взаимной спектральной плотности сигналов на входе и выходе фильтра Sgy(t(o).
Таким образом, амплитудно-фазовую характеристику фильтра без учета физической реализуемости следует выбирать так, чтобы взаимная спектральная плотность сигнала на входе и выходе фильтра была равна взаимной спектральной плотности входного и желаемого сигналов. Для некоррелированных сигнала y(t) и помехи e(t) спектральная плотность входного сигнала
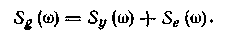

Таким образом, АФХ оптимального фильтра, найденная без
Взаимная спектральная плотность g(t) и tn(t) может быть выражена через характеристику эталонного оператора F3T(iu>):
86
учета физической реализуемости, имеет вид-

Если оказывается, что наиденная таким образом характеристика реализуема, она дает оптимальное решение. Однако знать эту характеристику полезно и тогда, когда она не реализуема, так как при подстановке ее в ,Sf (м) вычисленное значение среднеквадратичной ошибки дает тот нижний предел, меньше которого эта ошибка заведомо быть не може!
Перейдем к учету условий физической реализуемости. Аналогично задаче синтеза формирующего устройства преобразуем равенство (1 G6) так, чтобы зависящее от W слагаемое имело оригинал, равный нулю при t<0 Для этого проведем факторизацию Sg (со):
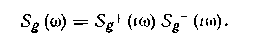
Оригинал первого сомножителя отличен от нуля при iO, а второго — при <0 В силу симметрии Sg(w) функции Sg+ и Sg- удовлетворяют равенству
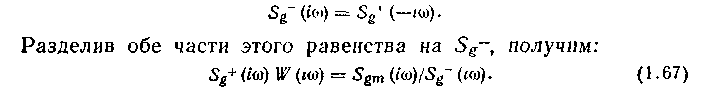
Левая часть этого равенства для физически реализуемой функции W(1ы) имеет оригинал, равный пулю при /<0, а при 10 выбором W можем сформировать нужную функцию. Наилучшему выбору W соответствует совпадение оригиналов от левой и правой час!ей равенства (1.67) при tO. После расщепления правой части равенства (1.67).
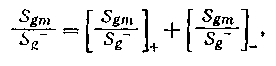
где знак «плюс» соответствует функции, оригинал которой отличен от нуля лишь при 0, получим для выбора W условие
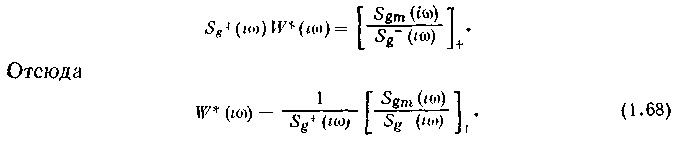
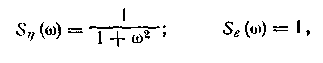
а корреляция полезного сигнала и помехи отсутствует
Пример. Решить задачу об оптимальном выделении сигнала у из смеси о помехой е, если спектральные плотности 5„ и Se имеют вид
87

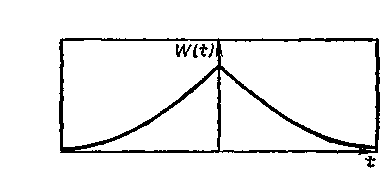
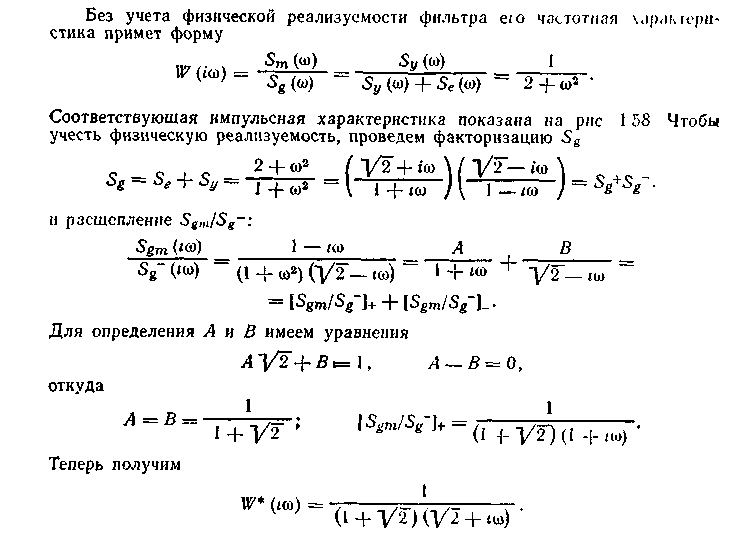
Оптимальным физически реализуемым фильтром оказалось апериодическое звено с оптимально найденными коэффициентом усиления и постоянной времени (экспоненциальный фильтр, см разд 33).
Обобщение задачи оптимальной фильтрации. Рассмотренная выше задача оптимальной фильтрации была обобщена в самых разных направлениях. Остановимся на одном из таких обобщений, связанным с тем, что ошибка системы для разных частот имеет различный вес. Этот фактор можно учесть, введя в критерий оптимальности весовую функцию, в результате чего он примет вид:

Чем больше весовая функция Н(w) на некоторой частоте, тем меньше ордината спектральной плотности ошибки, соответствующая оптимальному решению. Примером критерия, имеюще-
88
го вид (1.69), служат обобщенные интегральные критерии, где наряду с дисперсией ошибки г учитывается дисперсия ее производных Так, минимизация выражения

Весовая функция 1 { лщ2 на высоких частотах возрастает, поэтому спектр ошибки для оптимального фильтра окажется низкочастотным
Полученную выше формулу для расчета АФХ оптимального фильтра нетрудно распространить на случай функционала (1.69) Для этого нужно записать условие стационарности функционала 1ц по W. Очевидно, это условие будет отличаться от равенства (1 G5) только тем, что левая и правая его части будут содержать в качестве множителя функцию Н№. Получим:
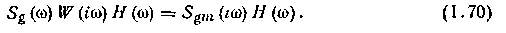
Для расчета оптимальной физически реализуемой АФХ фильтра проведем, как и выше, факторизацию Sg и Я, после чего поделим левую и правую части равенства (1.70) на произведение Sg-ff-. Получим:
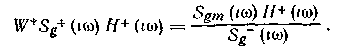
Для оптимального физически реализуемого фильтра оригиналы левой и правой частей этого условия должны совпадать при tQ. После расщепления правой части равенства придем к оптимальному решению в форме
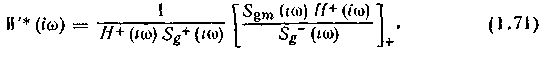
Оптимальное оценивание состояния объекта. В задаче оптимальной фильтрации предполагались известными спектральные плотности полезного сигнала и помехи, которые могут быть найдены посредством статистической обработки реализаций этих стационарных и эрг одических процессов При этом мы не предполагали известным механизм генерации этих сигналов. Между тем, если полезный сигнал представляет собой вектор-функцию у, характеризующую состояние технологического процесса, то приближенно известна его математическая модель; часть составляющих вектора состояния или некоторые зависящие от него переменные можно измерять и по результатам текущих измерений уточнять оценку у; сигнал, а в некоторых случаях и помехи, нельзя считать стационарными процессами.
89

Расчет функции y(t) при таких предположениях называют оцениванием состояния; если же в момент t нужно рассчитать y(t+t), то имеем задачу оценивания с прогнозом состояния. Схема, иллюстрирующая постановку задачи оценивания, приведена на рис. 1.59. Предполагаются известными модель обь-екта: статистические характеристики сигналов е, | и т|, характеризующие ошибки и случайные возмущения в модели, ошибки при измерении входных воздействий и при измерении переменных состояния соответственно; функция z(t) и вектор у0-Требуется оценить вектор у в момент t или (t+i). Основы теории оценивании развиты в работах Калмана и Бьюси [23]
Для систем регулирования модель объекта можно линеаризовать. Поэтому рассмотрим синтез алгоритма оценивания для линейных систем. Модель системы в векторно-матричной форме записи имеет вид (1.72), а модель измерений — вид (173):

В уравнениях (1.72) — (1.74) y(t)—n-мерный вектор состояния; z(t)—/-мерный вектор измеряемых выходов; e(t)—«-мерный вектор случайных возмущений; r\(t)—/-мерный вектор случайных ошибок измерений; | — случайная составляющая начальных условий; А — квадратная матрица (пХ); С — прямоугольная матрица (/Хп).
Здесь Т — интервал, в течение которого проводят наблюдения. Первое слагаемое в (1.75) представляет собой квадратичную
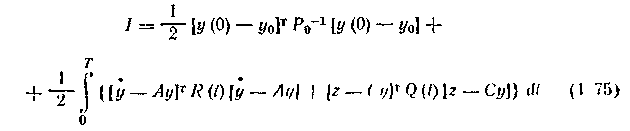
Требуется по наблюдениям за процессом z(t) найти такую оценку состояния процесса y(t), при которой достигает минимума критерий
