Если использовать разности высших порядков вплоть до n-го, то разностное уравнение 1

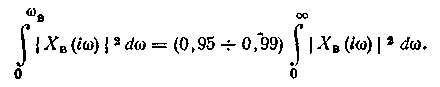
Комбинированную АСР можно рассматривать как двухсту­пенчатый фильтр для сигнала возмущения, состоящий из разо­мкнутой АСР и замкнутого контура, который является фильт­ром для определенных частот. Характерной особенностью за­мкнутой системы регулирования является наличие пика на ам­плитудно-частотной характеристике на рабочей частоте w_р (рис. 1.14), в окрестности которой он обладает наихудшими фильтрующими свойствами. Поэтому чаще всего условие при­ближенной инвариантности (1.25) для комбинированных АСР записывается для двух частот: w = 0 и w = w_p. При этом компен­сация возмущения на нулевой частоте обеспечивает инвариант­ность системы в установившихся режимах, если A_зс(w)<>0 при w = 0 (например, при использовании П-регулятора в замкнутом контуре), или если |Х_в(w)|—oo при w = 0 (например, при ступенчатых возмущениях).



На рис. 1.15 и 1.16 качественно показаны спектры ошибки
регулирования в одноконтурной АСР с пропорциональным ре­
гулятором (рис. 1.15) и в частично
инвариантной

АСР (рис. 1.16).

Выбор структуры реального компенсатора диктуется частотны-




36




ми характеристиками идеального компенсатора в диапазоне частот [0, сор]. Обычно компенсаторы выбирают как комбина­цию простейших линейных звеньев: апериодического первого порядка и реального дифференцирующего. В табл. 1.1 приведе­ны динамические характеристики наиболее распространенных типов компенсаторов.

Таким образом, расчет комбинированной частично инва­риантной АСР включает следующие этапы:

1. расчет настроек регулятора и определение рабочей час­
   тоты в одноконтурной системе регулирования;
   
2. вывод передаточной функции идеального компенсатора
   из условия инвариантности и анализ его реализуемости;
   
3. выбор реального компенсатора и определение его пара­
   метров из условия приближенной инвариантности в наиболее
   существенном для системы диапазоне частот.
   

Рассмотрим примеры расчета комбинированных систем ре­гулирования.




37




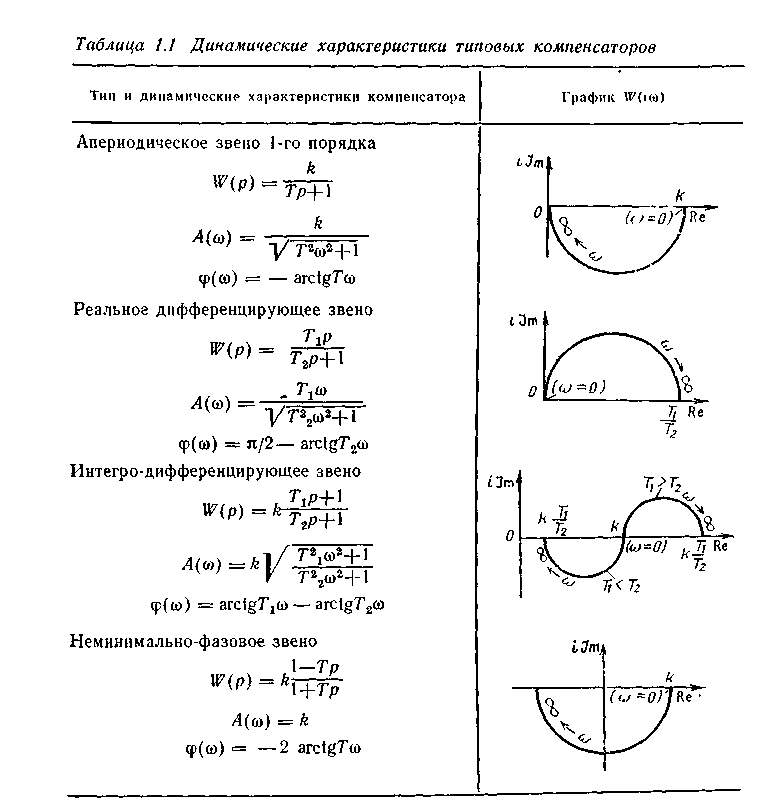
Пример 1. Динамические характеристики объекта по каналам возмуще­ния и регулирования описываются передаточными функциями



В комбинированной АСР используется П-регулятор с передаточной функци­ей R(р)= - S₁. Требуется рассчитать настройки регулятора, выбрать компен­сатор и определить его параметры из условия инвариантности на нулевой и рабочей частотах. Решение. Определяем настройки регулятора по методу Циглера — Ни­кольса. Из системы уравнений




38

определяем критическую частоту w _kp и критический коэффициент усиления регулятора s₁^kp, при которых замкнутая система регулирования будет на­ходиться на границе устойчивости:



Рабочую частоту w_p принимаем приближенно равной w_кр, а оптимальную настройку регулятора равной S₁* = 0,5S₁^KP = 0,917.

Передаточная функция компенсатора из условия инвариантности (1.20), с учетом (1.19) имеет вид:



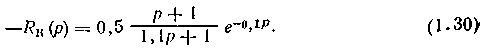
Так как компенсатор с передаточной функцией (1.30) не содержит звеньев с отрицательным чистым запаздыванием и степень полинома числи­теля не превосходит степени полинома знаменателя, идеальный компенсатор физически реализуем. Однако техническая реализация такого устройства до­статочно сложна, поскольку оно включает звенья чистого запаздывания, ре­альное дифференцирующее и апериодическое звено 1-го порядка. Поэтому целесообразно подобрать реальный компенсатор более простой структуры.

Для выбора типа реального компенсатора построим частотные характе­ристики идеального компенсатора в диапазоне частот [0, w_р]. Из уравнения (1.30) при p = iw получим:

амплитудно-частотная характеристика




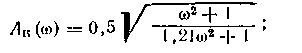
39



Так как в интервале w [0; 1,54] годограф R_K(iw) проходит в четвертом квадранте, в качестве реального компенсатора можно выбрать апериодиче­ское звено 1-го порядка или интегро-дифференцирующее звено. В первом случае (рис. 1.17а) система уравнений (см. табл. 1.1)



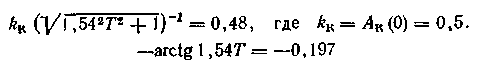
не имеет точного решения. Если принять приближенно T=0,145, то w_к(1,54) = = - 0,219 и A_к (1,54) =0,49.

Для интегро-дифференцирующего звена (рис. 1.17б) параметры Т₁ и Т₂ находим из системы уравнений



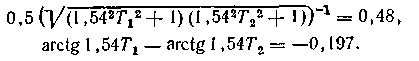
Получаем T₁=0,066; T₂=0,2.

Пример 2. Передаточные функции объекта и регулятора имеют вид:



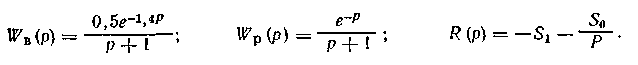
Расчет комбинированной системы регулирования, аналогичный рассмот­
ренному в примере 1, приводит к следующим результатам.

Оптимальные настройки регулятора и рабочая частота равны соответст­венно S₁*= 1,09; S₀* = 0,42; w_р = 2,02.

Идеальный компенсатор — звено чистого запаздывания, так как




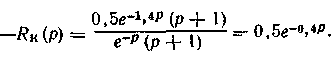
40


Рабочая частота на годографе R_K(iw) находится в четвертом квадран­те [ф_к (2,02)=—0,81], поэтому в качестве реального компенсатора выбираем устройство с передаточной функцией вида (см. табл. 1.1)



Параметры k_к и Т находим из условий



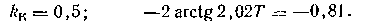
Отсюда Т=0,21. Частотные характеристики «идеального» и реального ком­пенсаторов показаны на рис. 1.18.

1.3.2. Каскадные АСР

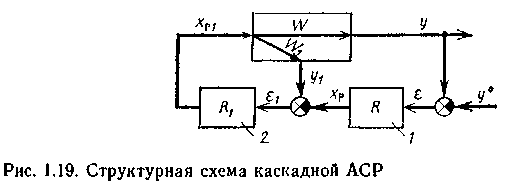
Каскадные системы применяют для автоматизации объектов, обладающих большой инерционностью по каналу регулирова­ния, если можно выбрать менее инерционную по отношению к наиболее опасным возмущениям промежуточную координату и использовать для нее то же регулирующее воздействие, что и для основного выхода объекта.

В этом случае в систему регулирования (рис. 1.19) вклю­чают два регулятора — основной (внешний) регулятор, служа­щий для стабилизации основного выхода объекта у, и вспомо­гательный (внутренний) регулятор, предназначенный для регу­лирования вспомогательной координаты у₁. Заданием для вспо-могатель'ного регулятора служит выходной сигнал основного регулятора.

Выбор законов регулирования определяется назначением регуляторов:

для поддержания основной выходной координаты на задан­ном значении без статической ошибки закон регулирования основного регулятора должен включать интегральную состав­ляющую;

от вспомогательного регулятора требуется прежде всего быстродействие, поэтому он может иметь любой закон регули­рования (в частности пропорциональный как наиболее простой и достаточно быстродействующий).

Сравнение одноконтурных и каскадных АСР показывает, что вследствие более высокого быстродействия внутреннего контура в каскадной АСР повышается качество переходного процесса, особенно при компенсации возмущений, поступаю­щих по каналу регулирования (как будет показано ниже, при




41





этом инерционность эквивалент­ного объекта благодаря внутрен­нему контуру снижается по сравнению с инерционностью основного канала регулирова­ния).

Если по условию ведения процесса на вспомогательную переменную накладывается ограничение (например, температу­ра не должна превышать предельно допустимого значения или соотношение расходов должно лежать в определенных преде­лах), то на выходной сигнал основного регулятора, который является заданием для вспомогательного регулятора, также накладывается ограничение. Для этого между регуляторами устанавливается устройство с характеристиками усилительного звена с насыщением.

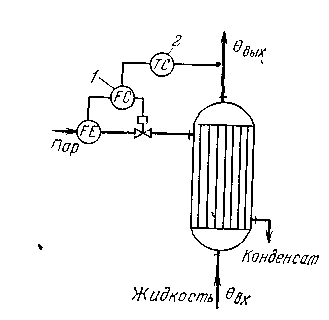
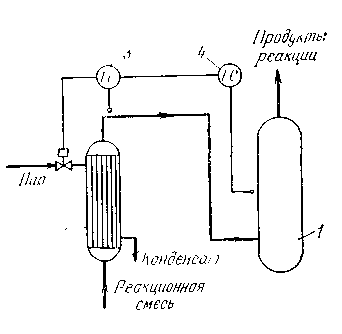
Примеры каскадных АСР технологических объектов. На рис. 1.20 приведен пример каскадной системы стабилизации температу­ры жидкости на выходе из теплообменника, в которой вспомо­гательным контуром является АСР расхода греющего пара. При возмущении по давлению пара регулятор 1 изменяет сте­пень открытия регулирующего клапана таким образом, чтобы поддержать заданный расход. При нарушении теплового ба­ланса в аппарате (вызванном, например, изменением входной температуры или расхода жидкости, энтальпии пара, потерь тепла в окружающую среду), приводящем к отклонению выход­ной температуры от заданного значения, регулятор температу­ры 2 корректирует задание регулятору расхода /.

В химико-технологических процессах часто основная и вспо­могательная координаты имеют одинаковую физическую при­роду и характеризуют значения одного и того же технологи­ческого параметра в разных точках системы (рис. 1.21).

На рис. 1.22 показаны фрагмент технологической схемы, включающий подогреватель реакционной смеси и реактор, и система стабилизации температуры в реакторе. Регулирую­щее воздействие — расход пара — подается на вход теплооб­менника. Канал регулирования, включающий два аппарата и

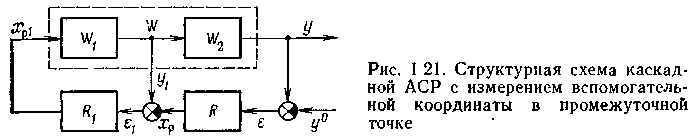
42





трубопроводы, является слож­
ной динамической системой с
большой инерционностью.

На объект действует ряд воз­мущений, поступающих в раз­ные точки системы, — давле­ние и энтальпия пара, темпе­ратура и расход реакционной смеси, потери тепла в реакторе и т. п. Для повышения быстро­действия системы регулирования применяют каскадную АСР, в которой основной регулируемой переменной является темпе­ратура в реакторе, а в качестве вспомогательной выбрана тем­пература смеси между теплообменником и реактором. Расчет каскадных АСР. Расчет каскадной АСР предпола­гает определение настроек основного и вспомогательного ре­гуляторов при заданных динамических характеристиках объ­екта по основному и вспомогательному каналам. Поскольку настройки основного и вспомогательного регуляторов взаимо­зависимы, расчет их проводят методом итераций.

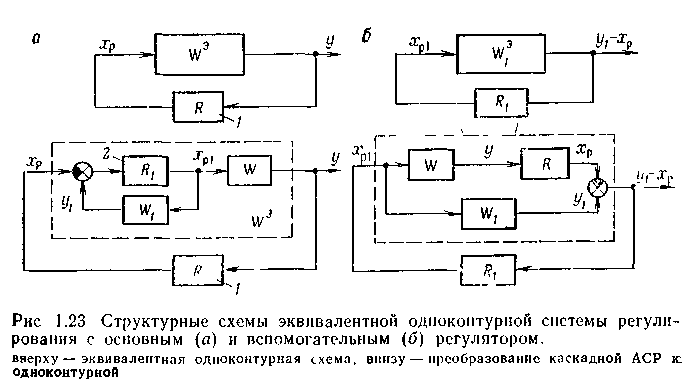
На каждом шаге итерации рассчитывают приведенную од­ноконтурную АСР, в которой один из регуляторов условно относится к эквивалентному объекту. Как видно из структур­ных схем на рис. 1.23, эквивалентный объект для основного регулятора / (рис. 1.23 а) представляет собой последовательное соединение замкнутого вспомогательного контура и основного

43

канала регулирования; передаточная функция его равна

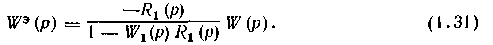
Эквивалентный объект для вспомогательного регулятора 2 (рис. 1.23,6) является параллельным соединением вспомога­тельного канала и основной разомкнутой системы. Его переда­точная функция имеет вид:



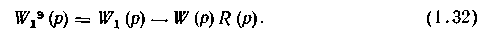
В зависимости от первого шага итерации различают два метода расчета каскадных АСР.

1-й метод. Расчет начинают с основного регулятора. Метод используют в тех случаях, когда инерционность вспомогатель­ного канала намного меньше, чем основного.

На первом шаге принимают допущение о том, что рабочая частота основного контура (w_р) намного меньше, чем вспомо­гательного (w_pl), И при w = w_р



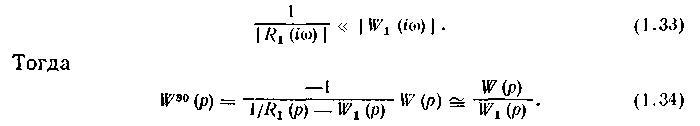
Таким образом, в первом приближении настройки 5° основно­го регулятора 1 не зависят от R¹(р) и находятся по W^эо(p).

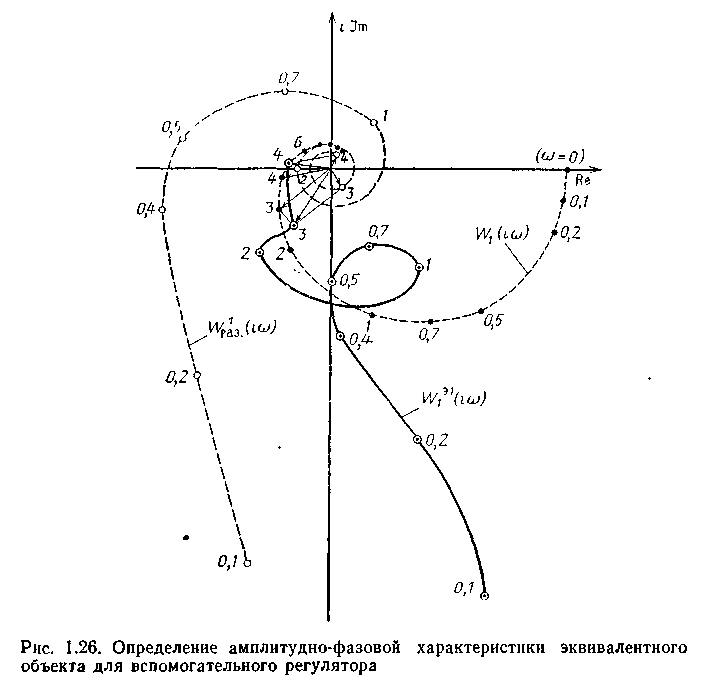
На втором шаге рассчитывают настройки вспомогательного регулятора S_l¹ для эквивалентного объекта (1.32) с передаточ­ной функцией W₁^э(p), в которую подставляют R(p,S°).

В случае приближенных расчетов ограничиваются первыми двумя шагами. При точных расчетах их продолжают до тех пор, пока настройки регуляторов, найденные в двух последова­тельных итерациях, не совпадут с заданной точностью. Блок-схема алгоритма расчета приведена на рис. 1.24, а. 2-й метод. Расчет начинают со вспомогательного регулятора. На первом шаге предполагают, что внешний регулятор отклю­чен, т. е.



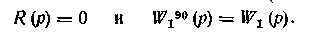
Таким образом, и первом приближении настройки вспомога­телыюго регулятора S₁° находят по одноконтурной АСР для вспомогательного канала регулирования. На втором шаге рас­считывают настройки основного регулятора по передаточной функции эквивалентного объекта W^э1(p) с учетом R₁(p, S₁°). Для уточнения настроек вспомогательного регулятора S₁¹ расчет проводят по передаточной функции (1.32) W₁^эо(p), в которую подставляют R(p,S¹). Расчеты проводят до тех пор, пока па-стройки вспомогательного регулятора, найденные в двух по­следовательных итерациях, не совпадут с заданной точностью (рис. 1.24,6).


44



Пример. Рассчитать настройки регуляторов в каскадной АСР, если пе-pедаточный функции объекта по основному и вспомогательному каналам и передаточные функции регуляторов соответственно равны



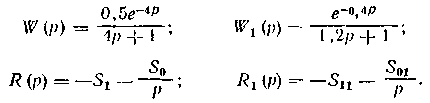
Для расчета одноконтурных АСР используем метод Циглера — Ни­кольса.

Из сравнения W (р) и W₁(p) видно, что инерционность вспомотательно­го канала намного меньше, чем основного (ti

45




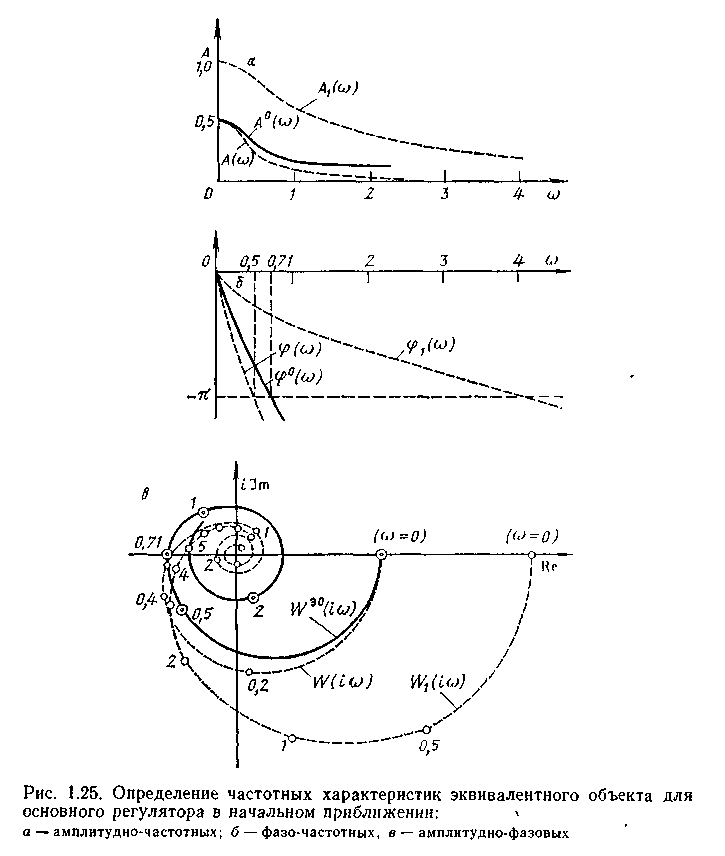
1. Расчет настроек основного регулятора (S₁⁰, S₀°, (w_p°). Следуя выражению (1 34), находим передаточную функцию эквивалент­ного объекта:




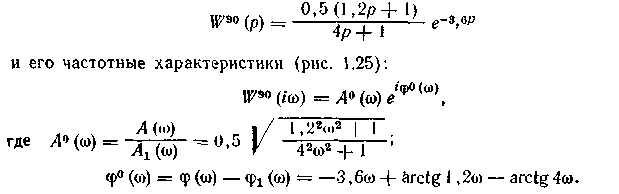
46

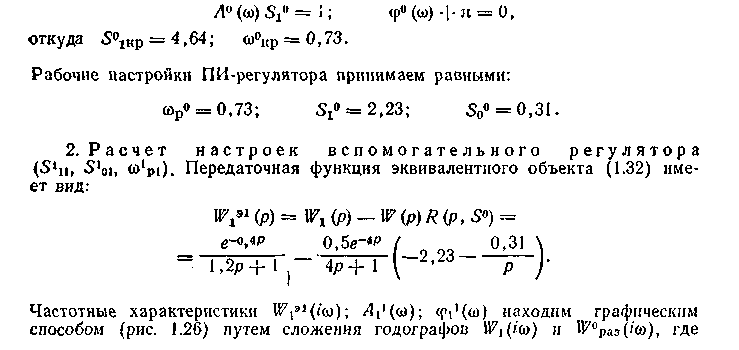
47



W°_paз (iw) =W(iw)R(iw, S°). Критические настройки регулятора S1кр и w¹ _kp находим из системы уравнений:



Рабочие настройки принимаем равными: S¹₁₁ = 2,82; S¹_o1 = 2,05; w¹ _1p=3,8.

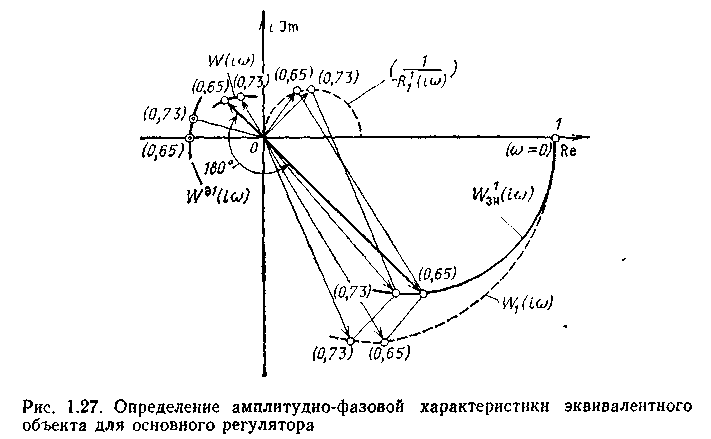
3. Уточнение настроек основного регулятора (S₁¹, So¹, (wp¹). Необходимость уточнения настроек регулятора S¹ возникает в том случае, если допущение (1.33) не выполняется с заданной точностью. Про­верка этого условия в данном примере показывает, что



т. е. l/|R₁¹(w_p)| соизмерима с A₁(w_р) (если принять допустимую погреш­ность при выполнении условия (1.33), равную 5%) и требуется дальнейшее уточнение настроек. Поэтому по формуле передаточной функции эквивалент­ного объекта W^э1 (р) находим его частотные характеристики в окрестности со = 0,73 (рис. 1.27) с учетом того, что




48



Критические и рабочие настройки регулятора 1 находим из условий




т. е. начиная с п. 2 необходимо повторить расчет.

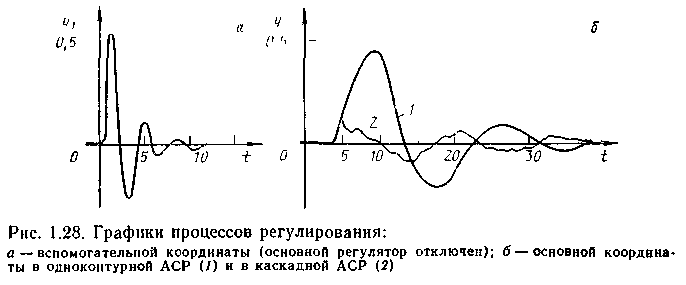
Результаты расчетов по итерациям сведены в таблицу. Их анализ показывает, что в рассмотренном примере рабочие частоты регуляторов в каскадной АСР незначительно отличаются от соответствующих частот в одноконтурных системах регулирования. При этом включение регуляторов в каскадную систему приводит к повышению рабочей частоты основного ре­гулятора и снижению рабочей частоты вспомогательного (см. рис. 1.28, а, б). Эта особенность каскадных АСР учитывается при выборе частотного диапазона, что позволяет сократить объем вычислений при расчетах частот­ных характеристик эквивалентных объектов.



Окончательный вывод об эффективности применения кас­кадной АСР по сравнению с одноконтурной делают на основе




49


сравнительного анализа результатов моделирования переход­ных процессов. Для рассмотренного примера на рис. 1.28 при­ведены графики процессов регулирования в одноконтурной и каскадной АСР при единичном ступенчатом возмущении по ка­налу регулирования. Как видно из сравнения кривых 1 и 2, динамическая ошибка регулирования в каскадной АСР снизи­лась почти в пять, а интегральный квадратичный критерий — почти в девять раз.

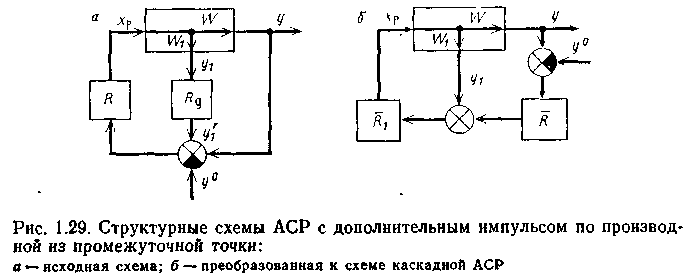
1.3.3. АСР с дополнительным импульсом по производной из промежуточной точки

Такие системы обычно применяют при автоматизации объек­тов, в которых регулируемый технологический параметр (на­пример, температура или состав) распределен по простран­ственной координате (как в аппаратах колонного или трубча­того типа). Особенность таких объектов состоит в том, что основной регулируемой координатой является технологический параметр на выходе из аппарата, возмущения распределены по длине аппарата, а регулирующее воздействие подается на его вход. При этом одноконтурные замкнутые АСР не обеспечи­вают должного качества переходных процессов вследствие большой инерционности канала регулирования.

Подача на вход регулятора дополнительного импульса из промежуточной точки аппарата дает опережающий сигнал, и регулятор включается в работу прежде, чем выходная коор­дината отклонится от заданного значения.

Для того чтобы обеспечить регулирование без статической ошибки, необходимо, чтобы в установившихся режимах допол­нительный импульс исчезал. С этой целью вспомогательную координату пропускают через реальное дифференцирующее звено, так что входной сигнал регулятора равен е= у+у^/1—у° (рис. 1.29,а). В установившихся режимах, когда у^/1 = 0, при е = 0, y = y⁰.

Эффективность введения дополнительного импульса зави­сит от точки его отбора. Выбор последней определяется в каж-