Если использовать разности высших порядков вплоть до n-го, то разностное уравнение 1
| Вид материала | Документы |
СодержаниеСистемы связанного регулирования. Автономные АСР. 1.4. Системы регулирования объектов с запаздыванием и нестационарных объектов |
- Частные производные и дифференциалы высших порядков п. Частные производные высших порядков, 190.6kb.
- Статья Тема: «Уравнения высших степеней с параметрами», 55.64kb.
- § Тема. Некоторые определения и обозначения, 1005.59kb.
- Статьи на русском, 122.97kb.
- Решение кубического уравнение в общем виде. От общего кубического уравнения к упрощённому, 14.77kb.
- У (к = 1,2,…). Однако на практике часто выгоднее выражать значения производных не через, 96.45kb.
- Содержание уравнения математической физики (нм-3) Уравнения математической физики (нп-3), 92.05kb.
- Определители 2-го и 3-го порядков: определения и применение к решению систем линейных, 42kb.
- Диффузия в биологических системах. Диффузия, 145.79kb.
- Методические рекомендации студентам, 215.81kb.
50
дом конкретном случае динамическими свойствами объекта и условиями его работы. Так, измерение y1 в начале аппарата равносильно дополнительному импульсу по возмущению, которое поступает по каналу регулирования. При этом дифференцирующее устройство играет роль динамического компенсатора возмущения. Измерение y1 па выходе объекта (у1=у) равносильно введению производной от основной координаты. Для каждого объекта можно выбрать оптимальное место отбора дополнительного импульса, при котором качество регулирования оказывается наилучшим.
Расчет подобных систем регулирования аналогичен расчету каскадных АСР после соответствующих преобразований. В приведенной каскадной АСР на рис. 1.29,б роль внешнего регулятора играет звено с передаточной функцией RД-1(p), а внутреннего — последовательно соединенные регулятор и дифференциатор, так что передаточные функции для приведенных регуляторов соответственно равны:
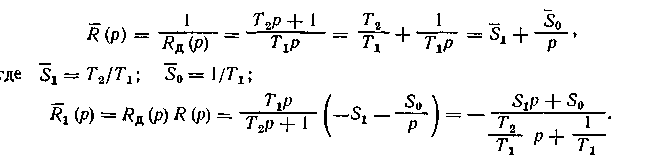
На достаточно высоких частотах, для которых выполняется условие Т2w >> 1, слагаемым 1/T1 можно пренебречь. Тогда, формула для R1(p) примет вид:
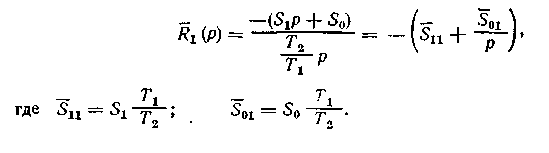
1.3.4. Взаимосвязанные системы регулирования
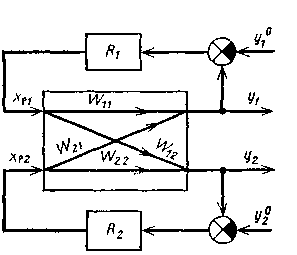
Объекты с несколькими входами и выходами, взаимно связанными между собой, называют многосвязными объектами (рис. 1.30, а). При отсутствии перекрестных связей, когда каждый вход влияет лишь на один выход, многосвязные объекты распадаются на односвязные (рис. 1.30, б), регулирование которых рассмотрено ранее. Однако подавляющее большинство химико-технологических процессов является сложными многосвязными объектами, а их системы регулирования оказываются взаимосвязанными.
Динамика многосвязных объектов описывается системой дифференциальных уравнений, а в преобразованном по Лапла-
51
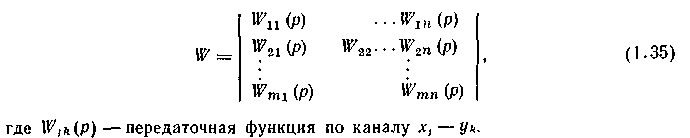
су виде — матрицей передаточных функции
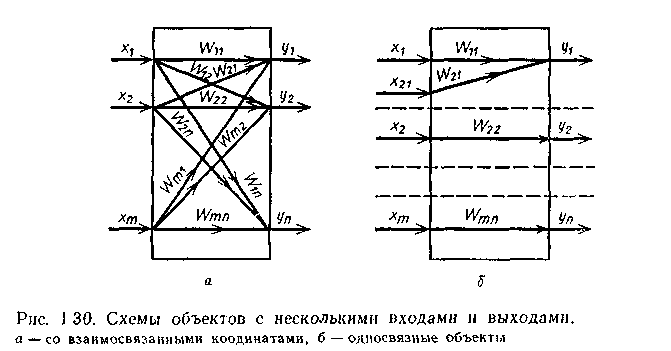
Для односвязных объектов WjK(p)=0 при j<>k, и матрица (1.35) превращается в диагональную.
Существует два различных подхода к автоматизации многосвязных объектов: несвязанное регулирование отдельных координат с помощью одноконтурных АСР; связанное регулирование с применением многоконтурных систем, в которых внутренние перекрестные связи объекта компенсируются внешними динамическими связями между отдельными контурами регулирования.
Каждый из этих методов обладает своими преимуществами и недостатками.
При несвязанном регулировании, если учитывают только основные каналы регулирования, расчет и наладку регуляторов проводят как для одноконтурных АСР. Этот метод можно применять в тех случаях, когда влияние перекрестных связей намного слабее, чем основных. При сильных перекрестных связях фактический запас устойчивости системы регулирования может оказаться ниже расчетного. Это приводит к низкому качеству регулирования, а в худшем случае — к потере устойчивости

52

вследствие взаимного влияния контуров регулирования.
Чтобы предотвратить возможность взаимного раскачивания, одноконтурные АСР следует рассчитывать с учетом внутренних связей и других контуров регулирования.
Это существенно усложняет расчет системы, но гарантирует заданное качество регулирования в реальной системе.
Связанные системы регулирования включают кроме основных регуляторов дополнительные динамические компенсаторы Насчет и наладка таких систем гораздо сложнее, чем одноконтурных АСР, что препятствует их широкому применению в промышленных системах автоматизации.
Рассмотрим методы расчета многосвязных систем регулирования на примере объекта с двумя входами и двумя выходами (рис. l.3l).
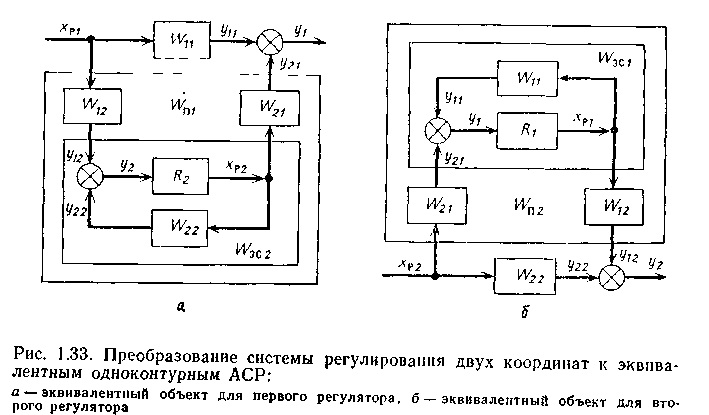
Системы несвязанного регулирования. Структурная схема системы представлена на рис. 1.32. Выведем передаточную функцию эквивалентного объекта в одноконтурной АСР с регулятором R1. Как видно из рис. 1.33, а, такой объект состоит из основного капала регулирования и связанной с ним параллельно сложной системы, включающей второй замкнутый контур регулирования и два перекрестных канала объекта
53
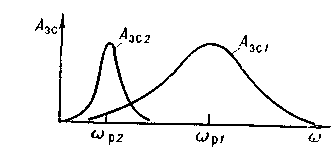
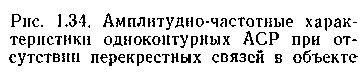
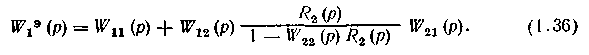
Передаточная функция эквивалентного объекта имеет вид:
Второе слагаемое в правой части уравнения (1.36) отражает влияние второго контура регулирования на рассматриваемую систему и по существу является корректирующей поправкой к передаточной функции прямого канала.
Аналогично для второго эквивалентного объекта (рис. 1.33,б) получим передаточную функцию в виде
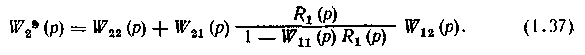
На основе формул (1.36) и (1.37) можно предположить, что если на какой-то частоте модуль корректирующей поправки будет пренебрежимо мал по сравнению с амплитудно-частотной характеристикой прямого канала, поведение эквивалентного объекта на этой частоте будет определяться прямым каналом.
Наиболее важно значение поправки на рабочей частоте каждого контура. В частности, если рабочие частоты двух контуров регулирования wp1 и wp2 существенно различны (например, wp1>>wp2 , как на рис. 1.34), то можно ожидать, что взаимное влияние их будет незначительным при условии.
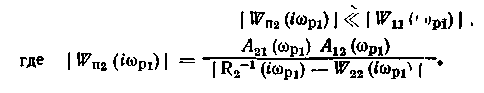
Наибольшую опасность представляет случай, когда инерционность прямых и перекрестных каналов приблизительно одинакова. Пусть, например, W11(p) = W12(p) = W21(p) = = W22(p) = W(p). Тогда для эквивалентных объектов при условии, что R1(p)=R2(p)=R(p), получим:
передаточные функции
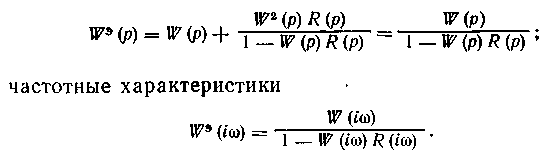
54
На границе устойчивости, согласно критерию Найквиста, получим:
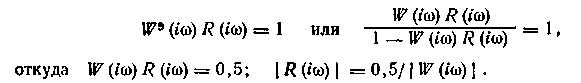
Так, настройка П-регулятора, при которой система находится па границе устойчивости, вдвое меньше, чем в одноконтурной АСР.
Для качественной оценки взаимного влияния контуров регулирования используют комплексный коэффициент связанности
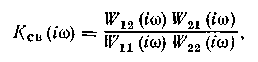
который обычно вычисляют па нулевой частоте (т. е. в установившихся режимах) и на рабочих частотах регуляторов wp1 и wp2. В частности, при w = 0 значение Ксв определяется отношением коэффициентов усиления по перекрестным и основным каналам:
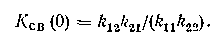
Если на этих частотах KCB~0, объект можно рассматривать как односвязнын; при KCB> 1 целесообразно поменять местами прямые и перекрестные каналы («перекрестное» регулирование); при 0
Системы связанного регулирования. Автономные АСР. Основой построения систем связанного регулирования является принцип автономности. Применительно к объекту с двумя входами и выходами понятие автономности означает взаимную независимость выходных координат y1 и y2 при работе двух замкнутых систем регулирования.
По существу, условие автономности складывается из двух условий инвариантности: инвариантности первого выхода у1 по отношению к сигналу второго регулятора Хр2 и инвариантности второго выхода y2 но отношению к сигналу первого регулятора Xp1.
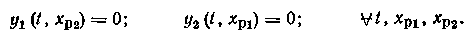
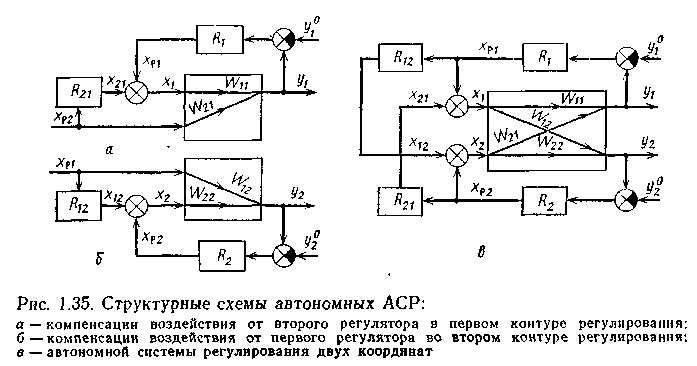
При этом сигнал xp1 можно рассматривать как возмущение для y2, а сигнал xp2 — как возмущение для y1. Тогда перекрестные каналы играют роль каналов возмущения (рис. 1.35). Для компенсации этих возмущений в систему регулирования вводят динамические устройства с передаточными функциями R12(p) и R21(p), сигналы от которых поступают на соответствующие каналы регулирования или на входы регуляторов.
55
По аналогии с инвариантными АСР передаточные функции компенсаторов R12(p) и R21(p), определяемые из условии автономности, будут зависеть от передаточных функций прямых и перекрестных каналов объекта и в соответствии с выражениями (1.20) и (1.20, а) будут равны:
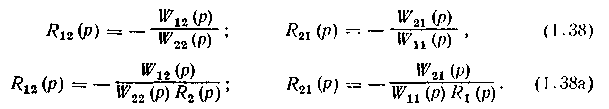
Так же, как в инвариантных АСР, для построения автоном-
ных систем регулирования важную роль играет физическая
реализуемость и техническая реализация приближенной авто
номности.
Условие приближенной автономности записывается для
реальных компенсаторов с учетом рабочих частот соотвеютвую
щих регуляторов:
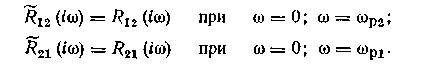
В химической технологии одним из самых сложных много-связных объектов является процесс ректификации. Даже в простейших случаях —при разделении бинарных смесей — в ректификационной колонне можно выделить несколько взаимосвязанных координат (рис. 1.36). Например, для регулирования процесса в нижней части колонны необходима стабилизация минимум двух технологических параметров, характеризующих материальный баланс но жидкой фазе и но одному из компонентов. Для этой цели обычно выбирают уровень жидкости в кубе и температуру под первой тарелкой, а в качестве регулирующих входных сигналов — расход греющего пара и отбор
56
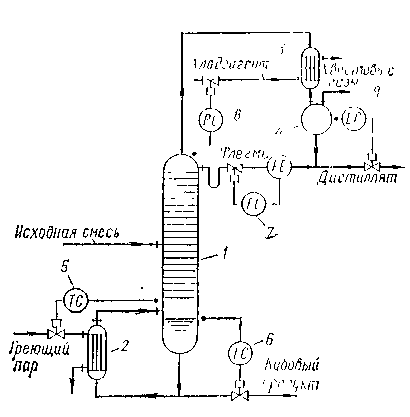

кубового продукта. Однако каждое из регулирующих воздействий влияет па оба выхода: при изменении расхода греющего пара изменяется интенсивность испарения кубового продукта, а вследствие этого — уровень жидкости и состав пара. Аналогично изменение отбора кубового продукта влияет не только на уровень в кубе, но и на флегмовое число, что приводит к изменению состава пара в нижней части колонны.
Для регулирования процесса в верхней части в качестве выходных координат можно выбрать давление и температуру пара, а в качестве регулирующих входных параметров — подачу хладоагента в дефлегматор и флегмы на орошение колонны. Очевидно, обе входные координаты влияют на давление и температуру в колонне в ходе тепловых и массообменных процессов.
Наконец, рассматривая систему регулирования температуры одновременно в верхней и нижней частях колонны подачей соответственно флегмы и греющего пара, также получим систему несвязанного регулирования объекта с внутренними перекрестными связями.
1.4. СИСТЕМЫ РЕГУЛИРОВАНИЯ ОБЪЕКТОВ С ЗАПАЗДЫВАНИЕМ И НЕСТАЦИОНАРНЫХ ОБЪЕКТОВ
1.4.1. Регулирование объектов с запаздыванием
Большинство технологических объектов характеризуется наличием чистого запаздывания в каналах регулирования. Запаздывание, возникающее при протекании потока вещества по длинным трубопроводам, носит название транспортного запаздывания. Запаздывание возможно и в результате использования в системе регулирования периодически действующих приборов или регуляторов — таких, как газовый хроматограф или цифровая вычислительная машина, включенная в цепь обратной связи.
57
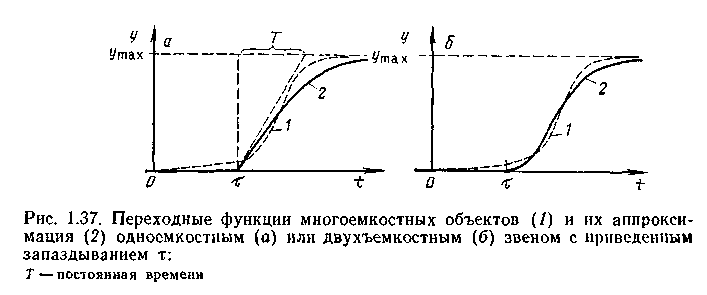
Многоемкостной объект с близкими по величине постоянными времени (например, тарельчатые аппараты) или объекте распределенными параметрами (трубчатые или наладочные аппараты) характеризуется переходными функциями с затянутым начальным участком (рис. 1.37), когда выходная координата практически не изменяется. В этом случае говорят о приведенном (эффективном) запаздывании, которое находят путем аппроксимации объекта одно- или двухъемкостным звеном с чистым запаздыванием.
Из-за значительного чистого запаздывания в объекте автоматизации существенно снижается качество регулирования при использовании обычных промышленных регуляторов.
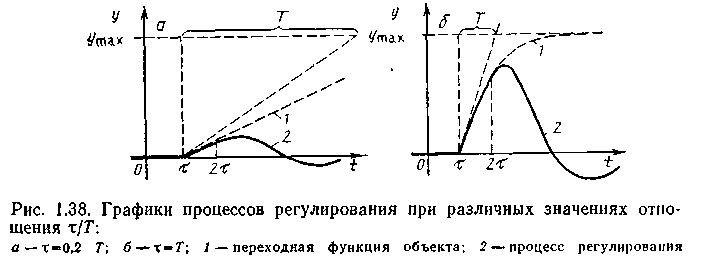
Даже при оптимальных настройках регуляторов качество процессов регулирования тем хуже, чем больше и само запаздывание, и ею отношение к постоянной времени объекта т/Т. Очевидно, на интервале 2т, пока регулирующее воздействие еще не сказывается на выходе объекта, процесс регулирования совпадает с переходной функцией объекта. При этом динамическая ошибка регулирования не может быть меньше, чем значение выхода апериодического звена при t = 2t. Если, например, Т = Т, то y(2t)=yan(T)~0,63 ymax, Где ymax — устано-
вившееся значение выхода объекта (рис. 1.38).
В практике регулирования объектов с запаздыванием принято считать, что если отношение т/Т превышает 0,2, то при-
58
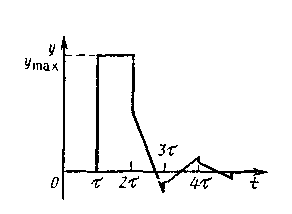

менение обычной непрерывной АСР со стандартным регулятором не обеспечит удовлетворительного качества регулирования. В предельном случае — для усилительного звена с чистым запаздыванием (т. е. Т = 0) —динамическая ошибка принимает максимально возможное значение — kx (где х — ступенчатое возмущение). Максимальный эффект, который может обеспечить в этом случае идеальная система регулирования,— сведение к нулю ошибки регулирования за время 2т. Реальный ПИ-регулятор, настроенный на заданную степень затухания переходного процесса, может справиться с этой задачей за время, приблизительно равное (5—6)т (рис. 1.39).
Примерно такой же эффект дает импульсное регулирование, когда регулятор подключают к объекту периодически (с периодом tо>т) на небольшой отрезок времени. При этом на объект подается регулирующее воздействие, пропорциональное ошибке. Оно остается постоянным до следующего момента включения регулятора, когда проявится эффект от предыдущего воздействия. При правильном выборе интервала to можно добиться некоторого уменьшения времени переходного процесса, однако значения интегральных критериев качества остаются приблизительно такими же, как и при непрерывном регулировании. Па рис. 1.40 приведены структурная схема и графики переходных процессов в импульсной АСР.
В тех случаях, когда к качеству переходных процессов в системе регулирования предъявляют высокие требования, целесообразно использовать специальные регуляторы или алгорит-
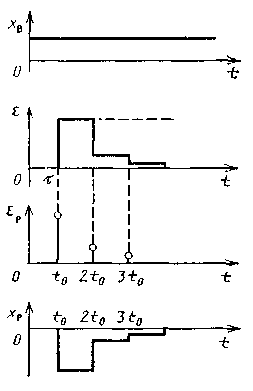

59
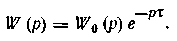
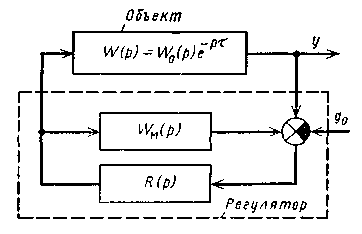

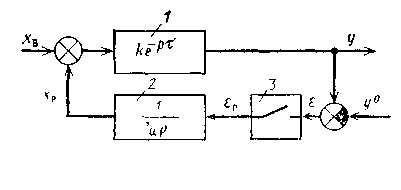
мы, обеспечивающие компенсацию чистого запаздывания. Примером такого регулятора является регулятор Смита [44]. Он представляет собой замкнутую систему, состоящую из обычного регулятора и модели объекта, включенной в линию обратной связи к регулятору (рис. 1.41). Уравнение модели объекта выводится из условия, чтобы желаемая передаточная функция объекта по каналу регулирования не содержала звена чистого запаздывания. Представим истинную передаточную функцию объекта в виде произведения
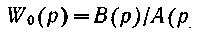
Здесь
) — дробно рациональная функция.
Тогда желаемая передаточная функция будет равна W0(p). Условие компенсации запаздывания запишется в виде равенства
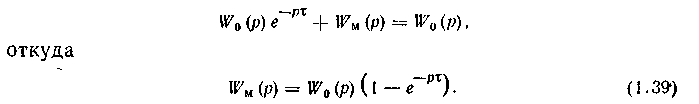
В этом случае характеристическое уравнение разомкнутой системы имеет вид:
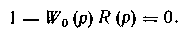
Следовательно, при одних и тех же параметрах настройки регуляторов запас устойчивости АСР с регулятором Смита выше, чем обычных АСР. Это означает, что при одинаковом запасе устойчивости АСР( например, при одной и той же степени затухания переходных процессов) для регулятора Смита можно
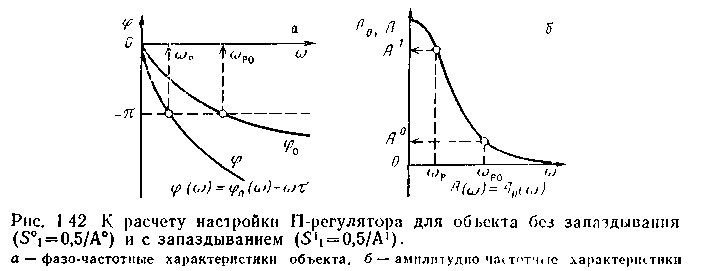
60
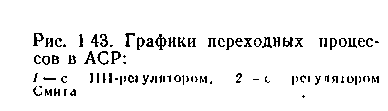
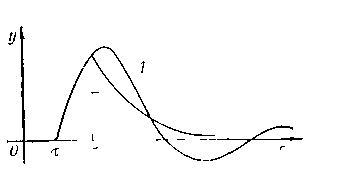
принять более высокую рабочую частоту и больший коэффи -циеит усиления, что обеспечит лучшее качество регулирование (рис. 1.42). Для сравнения на рис. 1.43 приведены процессы регулирования одного и того же объекта ПИ-регулятором и регулятором Смита.
К недостаткам регулятора Смита, кроме сложности его структуры и аппаратурной реализации, относится высокая чувствительность к параметрам настройки модели. Ошибки в на -стройке модели, вызванные неточностью априорных знаний о характеристиках объекта или нестационарностью его свойств , могут привести не только к ухудшению качества переходных процессов, но и к потере устойчивости системой регулирования . Поэтому практические рекомендации по выбору систем регули -рования объектов с чистым запаздыванием заключаются в следующем*:
использование специальных регуляторов с компенсацией запаздывания целесообразно лишь при отношении т/Т>0,5—-0,7;
при изменении параметров объекта более чем на 20% oт поминальных значений требуется коррекция настроек параметров модели;
при наличии высокочастотных возмущений в объекте использование регуляторов с компенсацией запаздывания нецелесообразно;
реализация регуляторов с компенсацией запаздывания программным способом наиболее эффективна при использовании ЭВМ в режиме супервизорного или непосредственного цифрового управления (см. гл. 7).
В ряде случаев динамические характеристики объекта таковы, что наилучший (в отношении качества переходных процессов) способ регулирования неэкономичен, поэтому в статическом режиме регулирующее воздействие должно отсутствовать либо иметь минимально возможное значение. Пусть по каналу с передаточной функцией W1(p) (рис. 1.44) объект обладает меньшим запаздыванием, чем по каналу с передаточной функцией W2(p). Чтобы в статическом режиме регулирующее воздействие xp1 было равно пулю, а динамические характеристики системы были близки к характеристикам системы с объектом,
- М. Хаджийски. Проектиране на системи за управление на технолошчни обекти. Ч I. София, Технике 1982.
