Бийск 2005

Вид материала

Содержание

3.2 Оценка аннуитетов
3.2.1 Оценка срочных аннуитетов
А) и процентной ставке (r
3.3 Автоматизация исчисления характеристик аннуитетов
ПЛТ (ставка; кпер; нс; [бс]; [тип])
=ставка (в7в6; в10; в8; в9; в11)
Вопросы для самоконтроля
FV=; б) современной величины PV

Подобный материал:

1 2 3 4 5 6 7 8 9 10 11

3.2 Оценка аннуитетов

Одним из ключевых понятий в финансовых и коммерческих расчетах является понятие аннуитета. Логика, заложенная в схему аннуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инвестиционных проектов, а также в анализе аренды.

3.2.1 Оценка срочных аннуитетов

Аннуитет представляет собой частный случай денежного потока, а именно, это поток, в котором денежные поступления в каждом периоде одинаковы по величине. Если число равных временных интервалов ограничено, аннуитет называется срочным. В этом случае: С₁=С₂=…=С_n=А. Как и в общем случае, выделяют два типа аннуитетов: постнумерандо и пренумерандо (рисунок 3.6).

Рисунок 3.6 – Виды срочных аннуитетов

Примером срочного аннуитета постнумерандо могут служить регулярно поступающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренд по истечении очередного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления достаточной суммы для крупной покупки.

Прямая задача оценки срочного аннуитета при заданных величинах регулярного поступления ( А) и процентной ставке (r) предполагает оценку будущей стоимости аннуитета. Как следует из логики, присущей схеме аннуитета, наращенный денежный поток имеет вид:

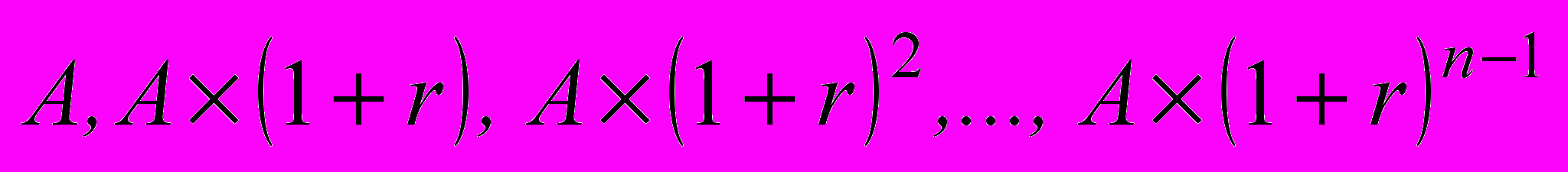. (3.8)

Формула для постнумерандо трансформируется следующим образом:

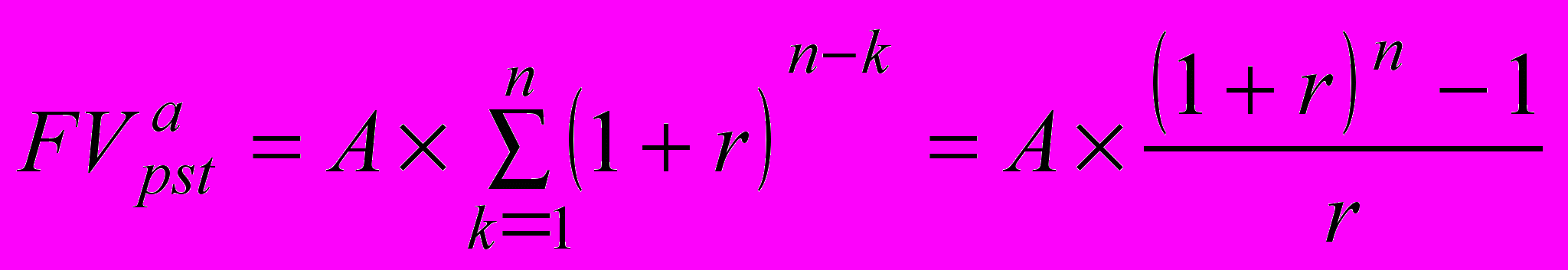. (3.9)

Общая постановка обратной задачи оценки срочного аннуитета постнумерандо также достаточно наглядна. В этом случае производится оценка будущих денежных поступлений с позиции текущего момента времени, под которым в данном случае понимается момент времени, с которого начинают отсчитываться равные временные интервалы, входящие в аннуитет.

Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо PV_pst имеет вид:

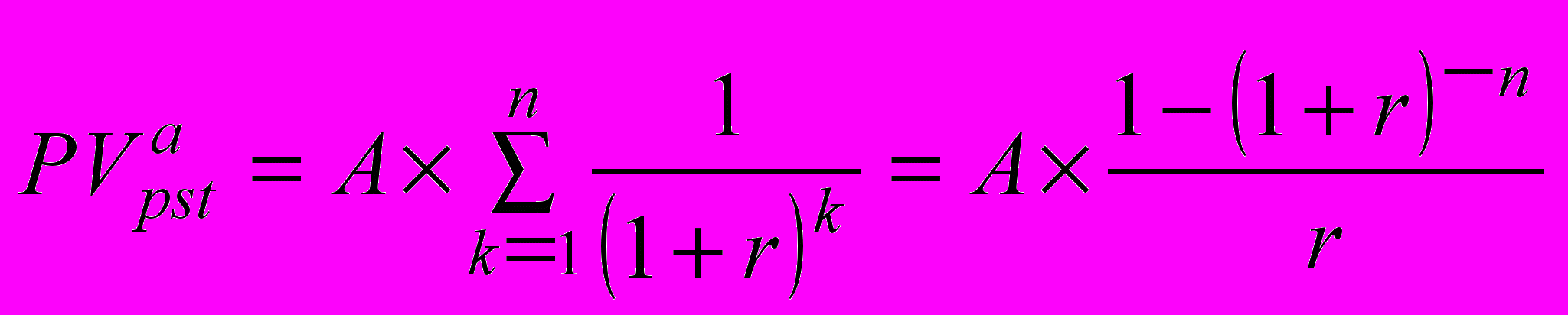. (3.10)

Величина К – дисконтирующий множитель:

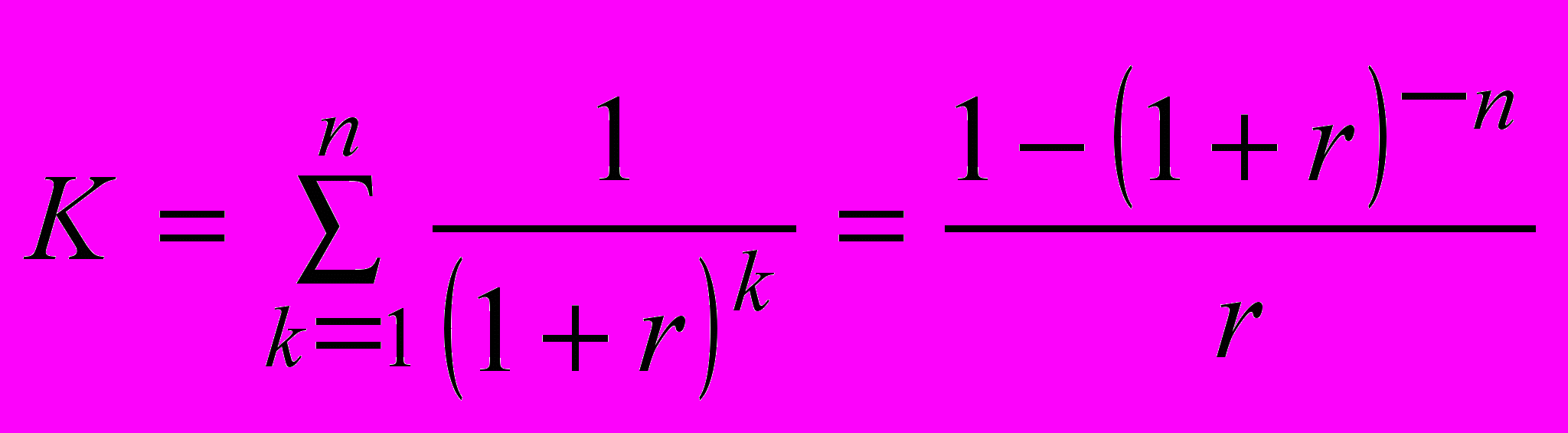. (3.11)

Экономический смысл дисконтирующего множителя заключается в следующем: он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы, продолжающего n равных периодов с заданной процентной ставкой r.

Соответствующие расчетные формулы для аннуитета пренумерандо:

 будущая стоимость аннуитета пренумерандо

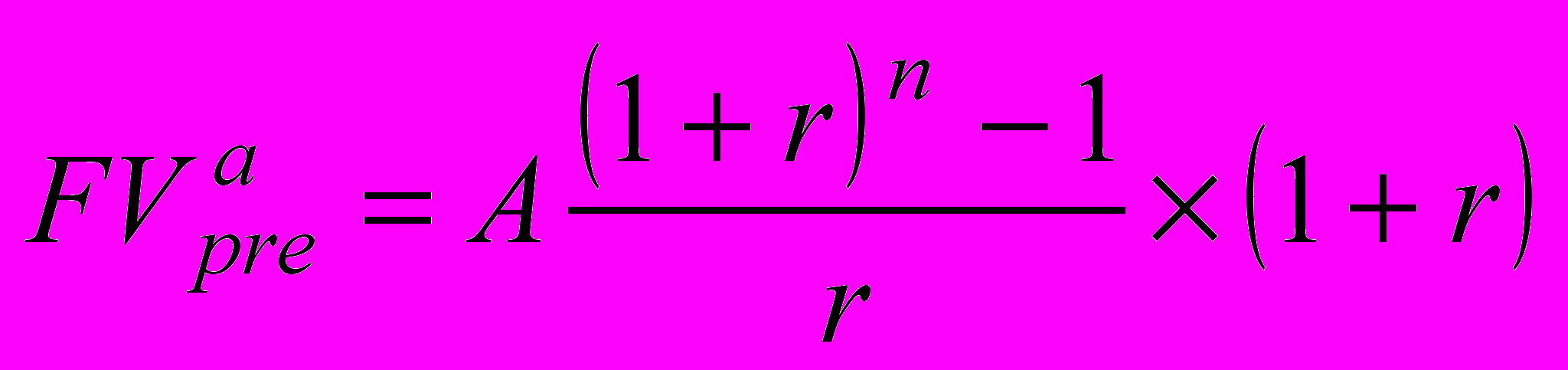; (3.12)

 приведенная стоимость аннуитета пренумерандо

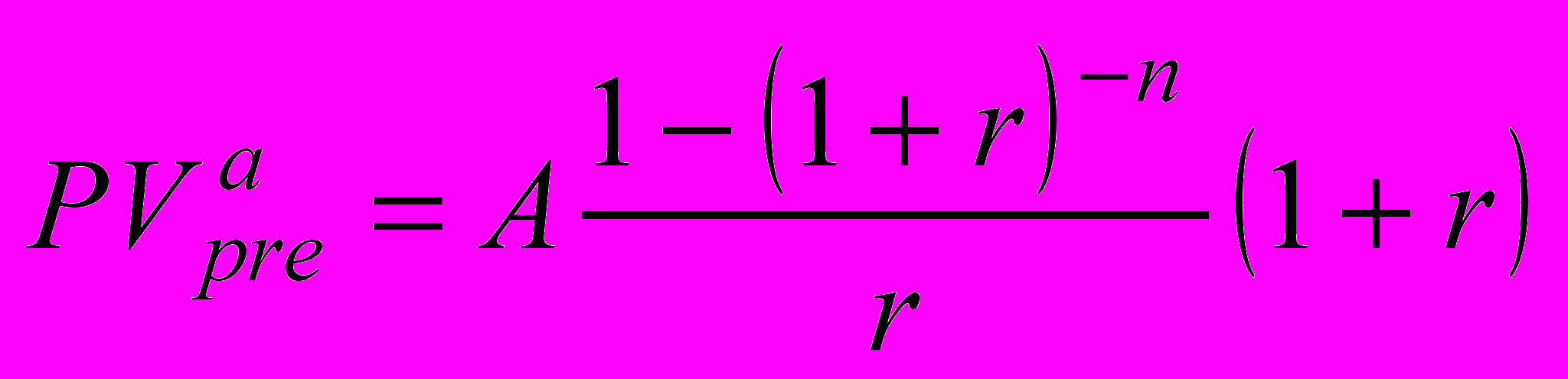. (3.13)

Пример 3.1 Вам предложено инвестировать 100 млн. руб. на срок 5 лет при условии возврата этой суммы частями (ежегодно по 20 млн. руб.). По истечении пяти лет выплачивается дополнительно вознаграждение в размере 30 млн. руб. Принимать ли это предложение, если можно «безопасно» депонировать деньги в банк из расчета 12% годовых?

Для принятия решения необходимо рассчитать и сравнить две суммы. При депонировании денег в банк к концу пятилетнего периода на счете будет сумма: F_s=P (1+r)⁵=100 (1+0,12)⁵=176 млн. руб.

В отношении альтернативного варианта, предусматривающего возмещение вложенной суммы частями, предполагается, что ежегодные поступления в размере 20 млн. руб. можно немедленно пускать в оборот, получая дополнительные доходы. Если нет других альтернатив по эффективному использованию этих сумм, их можно депонировать в банк. Денежный поток в этом случае можно представить двояко:

а) как срочный аннуитет постнумерандо с А=20, n=5, r=20% и единовременное получение суммы в 30 млн. руб.;

б) как срочный аннуитет пренумерандо с А=20, n=4, r=20% и единовременное получение сумм в 20 и 30 млн. руб.

В первом случае на основании формулы (3.9) имеем:

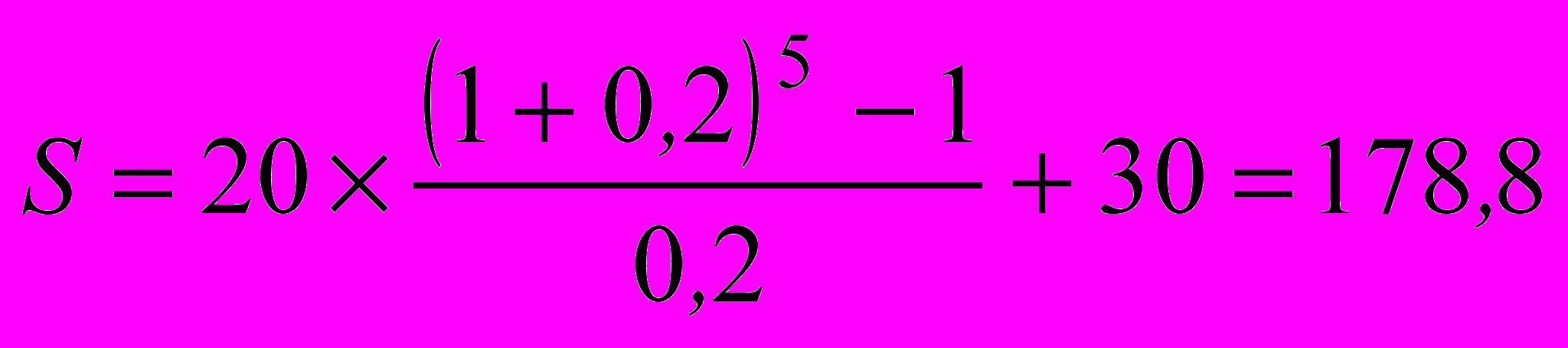млн. руб.

Во втором случае на основании формулы 3.12 имеем:

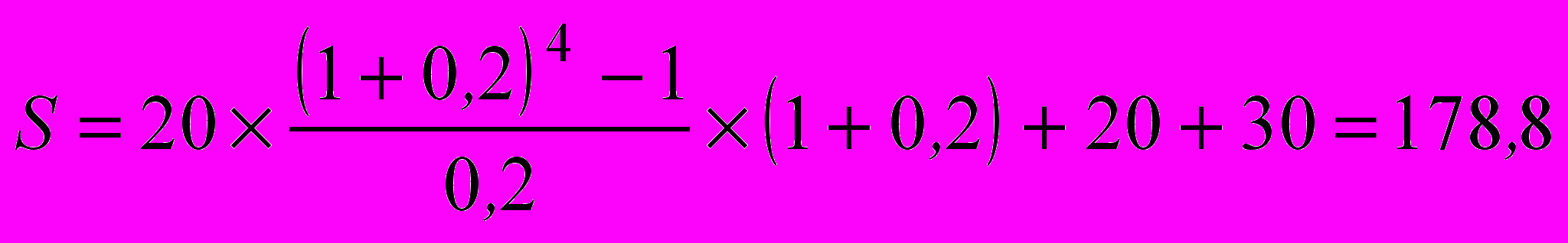млн. руб.

Естественно, что оба варианта привели к одинаковому ответу. Таким образом, общая сумма капитала к концу пятилетнего периода будет складываться из доходов от депонирования денег в банке
(128,8 млн. руб.), возврата доли от участия в венчурном проекте за последний год (20 млн. руб.) и единовременного вознаграждения
(30 млн. руб.). Общая сумма составит 178,8 млн. руб. Предложение экономически выгодно.

3.3 Автоматизация исчисления характеристик аннуитетов

Расчет будущей стоимости простого аннуитета и его современной стоимости основан на тех же принципах, что и для элементарных платежей. Соответственно, применимы те же самые показатели, используемые Excel.

Функция ПЛТ служит для расчета величины периодического платежа.

Функция ПЛТ (ставка; кпер; нс; [бс]; [тип]) применяется, если необходимо определить величину периодического платежа CF.

Следует отметить, что начисление процентов в начале каждого периода всегда приводит к большему значению будущей величины аннуитета за тот же срок.

При начислении процентов m раз в году величины r и n корректируются так же, как и в предыдущих примерах.

Для решения задач необходимо преобразовать предыдущий шаблон, воспользовавшись командами редактирования Excel (рисунок 3.7). Формулы шаблона приведены в таблице 3.1.

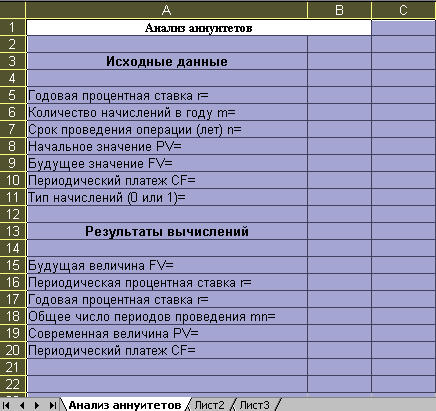
Рисунок 3.7 – Шаблон для анализа аннуитетов

Таблица 3.1 – Формула шаблона (аннуитеты)

Ячейка	Формула
В15	=БС (В5/В6; В6В7; В0; В8; В11)
В16	=СТАВКА (В7В6; В10; В8; В9; В11)
В17	=В15В7
В18	=КПЕР (В5/В6; В10; В8; В9; В11)
В19	=ПС (В5/В6; В7В6; В10; В9; В11)
В20	=ПЛТ (В5/В6; В7В6; В8; В9; В11)

Если при решении задач требуется одновременный анализ нескольких альтернатив, скопируйте в соседние колонки необходимое количество раз блок ячеек, содержащий формулы.

Вопросы для самоконтроля

1. Что такое аннуитет? Приведите примеры финансовых операций, денежные потоки которых представляют собой аннуитет.

2. Напишите формулы для исчисления следующих характеристик обыкновенного аннуитета:

а) будущей величины FV=;

б) современной величины PV=;

в) процентной ставки r=;

г) периодического платежа CF=;

д) срока операции n=.

3. Поясните, что такое приведенная стоимость денежного потока?

4. Как можно оценить потоки пренумерандо и постнумерандо?

5. Дайте определение срочному аннуитету.

Задачи для самостоятельного решения

Период платежей по аннуитету 5 лет. Интервал платежей по аннуитету составляет 1 год. Сумма каждого отдельного платежа 1000 руб. Процентная ставка 10%. Рассчитать будущую стоимость аннуитета: а) пренумерандо; б) постнумерандо.
Работник выходит на пенсию. Фирма предлагает пять вариантов выплаты:

а) в виде единовременного пособия – 100 тыс. руб.;

б) ежегодную выплату 15000 руб. на протяжении 10 лет;

в) единовременное пособие в размере 60 тыс. руб. и по 5 тыс. руб. ежегодно в течение 10 лет;

г) ежегодную выплату в размере 10 тыс. руб. в течение 10 лет и единовременную выплату 100 тыс. руб. по истечении 10 лет;

д) ежеквартальную выплату в размере 3000 руб. в течение 10 лет и единовременное пособие в размере 25 тыс. руб.

Какой вариант выбрали бы Вы, если процентная ставка равна 10%?

Определить ориентировочную рыночную стоимость облигации номиналом 100 тыс. руб. при условии, что срок погашения 3 года, купонная ставка 10% годовых, ставка банковского процента 4% годовых.
Определить ориентировочную стоимость акции номиналом 1000 руб., если она будет обеспечивать поступление дивидендов в размере 20% ежегодно, по крайней мере, в течение 15 лет. Ставка банковского процента составляет 15% годовых.
Предприятие «Феликс» планирует ежегодные отчисления в сумме 100 тыс. руб. для создания денежного фонда. Процентная ставка равна 10%. Какова будет величина фонда через: а) 5 лет; б) 10 лет; в) 12 лет?
Какова текущая стоимость аннуитета, выплачиваемого по 10000 руб. ежегодно в течение 8 лет при ставке 5%?
Сколько лет понадобится для выплаты долга в количестве
10 тыс. руб. равными платежами по 2309,75 руб. при процентной ставке в 5%?
Работник Иванов уходит на пенсию. Фирма, где он работает, предлагает два варианта выплаты пенсии: а) в виде единовременного пособия в количестве 55 тыс. руб.; б) ежегодную выплату 10000 руб. на протяжении 10 лет. Какой вариант предпочтительнее, если ставка по банковским депозитам равна 10%?
Определить текущую стоимость 3-годичной облигации с номиналом в размере 1000 ден.ед. и купонной ставкой 8%, выплачиваемой 4 раза в год. Норма дисконта (рыночной ставки) 12% и 6%.
Рассчитайте приведенную стоимость денежного потока постнумерандо (тыс. руб.): 12, 15, 9, 25, если коэффициент дисконтирования r = 12%.
Ежегодно делается взнос в банк в размере 1000 ден. ед. Какая сумма будет на счете через 10 лет, если взнос делается одной суммой в начале каждого года, а банк начисляет 12% годовых один раз в два
года.
На ежеквартальные взносы в банк в размере 100 тыс. руб. по схеме пренумерандо банк начисляет 12% годовых: а) раз в год; б) раз в полгода. Какая сумма будет на счете через 3 года?
Предполагается в течение шести лет ежегодно вкладывать по 4000 ден. ед. в облигации с купонной доходностью 7% (схема пренумерандо). Чему равна сумма к получению в конце периода?
Каков ваш выбор – получение 5000 ден. ед. через год или 12000 ден. ед. через шесть лет, если коэффициент дисконтирования равен: а) 0%; б) 12%; в) 20%?
Рассчитайте будущую стоимость 1000 ден. ед. для следующих ситуаций:

а) 5 лет, 8% годовых, ежегодное начисление процентов;

б) 5 лет, 8% годовых, полугодовое начисление процентов;

в) 5 лет, 8% годовых, ежеквартальное начисление процентов.

Предприятие приобрело здание за 20000 ден. ед. на следующих условиях: а) 25% стоимости оплачиваются немедленно; б) оставшаяся часть погашается равными годовыми платежами в течение 10 лет с начислением 12% годовых на непогашенную часть кредита по схеме сложных процентов. Определите величину годового платежа.
Что более предпочтительнее – получить 2000 ден. ед. сегодня или 5000 ден. ед. через 8 лет, если коэффициент дисконтирования равен 9%?
Какие условия предоставления кредита более выгодны банку: а) 28% годовых, начисление ежеквартальное; б) 30% годовых, начисление полугодовое?
Стоит ли покупать ценную бумагу за 5500 ден. ед. генерирующую ежегодный доход в размере 1000 ден. ед. в течение семи лет, если коэффициент дисконтирования равен 8%?
Фирме необходимо накопить 2 млн. дол., чтобы через 10 лет приобрести здание под офис. Наиболее безопасным способом накопления является приобретение безрисковых государственных ценных бумаг, генерирующих годовой доход по ставке 8% при полугодовом начислении процентов. Каким должен быть первоначальный вклад фирмы?

Blog

Содержание

3.2 Оценка аннуитетов

3.2.1 Оценка срочных аннуитетов

3.3 Автоматизация исчисления характеристик аннуитетов