А. С. Гринберг О. Б. Плющ Б. В. Новыш Теория вероятностей и математическая статистика Курс лекций
| Вид материала | Курс лекций |
СодержаниеАлгебра событий Противоположным (дополнительным) Свойства операций над событиями Алгебра и сигма-алгебра событий |
- Рабочая программа дисциплины "теория вероятностей и математическая статистика", 112.61kb.
- Конспект лекций по курсу "Теория вероятностей и математическая статистика", 1417.24kb.
- Рабочая учебная программа дисциплины (модуля) Теория вероятностей и математическая, 217.23kb.
- Примерная программа наименование дисциплины «теория вероятностей и математическая статистика», 165.37kb.
- Рабочая программа учебной дисциплины теория вероятностей и математическая статистика, 830.1kb.
- Рабочая программа учебной дисциплины «Теория вероятностей и математическая статистика», 165.42kb.
- Программа курса лекций "Теория вероятностей и математическая статистика", 18.69kb.
- Примерная рабочая программа по дисциплине: «теория вероятностей, математическая статистика, 83.07kb.
- Программа по дисциплине «Теория вероятностей и математическая статистика» для студентов, 206.05kb.
- Программа дисциплины «теория вероятностей и математическая статистика» Для направления, 198.58kb.
Алгебра событий
Операции над событиями (сумма, разность, произведение)
С каждым испытанием связан ряд интересующих нас событий, которые, вообще говоря, могут появляться одновременно. Например, при бросании игральной кости (т.е. кубика, на гранях которого имеются очки 1, 2, 3, 4, 5, 6) событие
 есть выпадение двойки, а событие
есть выпадение двойки, а событие  – выпадение четного числа очков. Очевидно, что эти события не исключают друг друга.
– выпадение четного числа очков. Очевидно, что эти события не исключают друг друга.Пусть все возможные результаты испытания осуществляются в ряде единственно возможных частных случаев, взаимно исключающих друг друга. Тогда:
- каждый исход испытания представляется одним и только одним элементарным событием;
- всякое событие
 , связанное с этим испытанием, есть множество конечного или бесконечного числа элементарных событий;
, связанное с этим испытанием, есть множество конечного или бесконечного числа элементарных событий;
- событие
 происходит тогда и только тогда, когда реализуется одно из элементарных событий, входящих в это множество.
происходит тогда и только тогда, когда реализуется одно из элементарных событий, входящих в это множество.
Другими словами, задано произвольное, но фиксированное пространство элементарных событий
 , которое можно представить в виде некоторой области на плоскости. При этом элементарные события
, которое можно представить в виде некоторой области на плоскости. При этом элементарные события  – это точки плоскости, лежащие внутри
– это точки плоскости, лежащие внутри  . Поскольку событие отождествляется с множеством, то над событиями можно совершать все операции, выполнимые над множествами. То есть, по аналогии с теорией множеств, строится алгебра событий. В частности, определены следующие операции и отношения между событиями:
. Поскольку событие отождествляется с множеством, то над событиями можно совершать все операции, выполнимые над множествами. То есть, по аналогии с теорией множеств, строится алгебра событий. В частности, определены следующие операции и отношения между событиями: 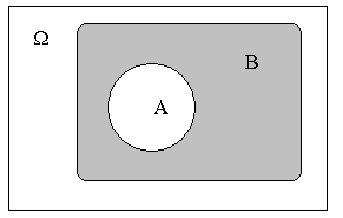  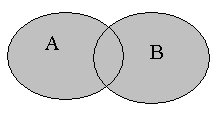  |  (отношение включения множеств: множество (отношение включения множеств: множество  является подмножеством множества является подмножеством множества  ) – событие A влечет за собой событие В. Иначе говоря, событие В происходит всякий раз, как происходит событие A. ) – событие A влечет за собой событие В. Иначе говоря, событие В происходит всякий раз, как происходит событие A. (отношение эквивалентности множеств) – событие (отношение эквивалентности множеств) – событие  тождественно или эквивалентно событию тождественно или эквивалентно событию  . Это возможно в том и только в том случае, когда . Это возможно в том и только в том случае, когда  и одновременно и одновременно  , т.е. каждое из них происходит всякий раз, когда происходит другое. , т.е. каждое из них происходит всякий раз, когда происходит другое. ( ( ) – сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий ) – сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий  или или  (не исключающее логическое «или»). В общем случае, под суммой нескольких событий понимается событие, состоящее в появлении хотя бы одного из этих событий. (не исключающее логическое «или»). В общем случае, под суммой нескольких событий понимается событие, состоящее в появлении хотя бы одного из этих событий. |
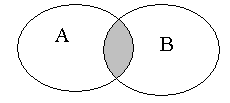  |  ( ( ) – произведение событий. Это событие, состоящее в совместном осуществлении событий ) – произведение событий. Это событие, состоящее в совместном осуществлении событий  и и  (логическое «и»). В общем случае, под произведением нескольких событий понимается событие, состоящее в одновременном осуществлении всех этих событий. Таким образом, события (логическое «и»). В общем случае, под произведением нескольких событий понимается событие, состоящее в одновременном осуществлении всех этих событий. Таким образом, события  и и  несовместны, если произведение их есть событие невозможное, т.е. несовместны, если произведение их есть событие невозможное, т.е.  . . |
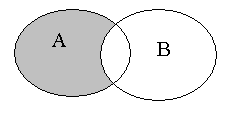  |  (множество элементов, принадлежащих (множество элементов, принадлежащих  , но не принадлежащих , но не принадлежащих  ) – разность событий. Это событие, состоящее из исходов, входящих в ) – разность событий. Это событие, состоящее из исходов, входящих в  , но не входящих в , но не входящих в  . Оно заключается в том, что происходит событие . Оно заключается в том, что происходит событие  , но при этом не происходит событие , но при этом не происходит событие  . . |
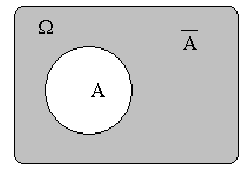  | Противоположным (дополнительным) для события  (обозначается (обозначается  ) называется событие, состоящее из всех исходов, которые не входят в ) называется событие, состоящее из всех исходов, которые не входят в  . .Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Событие  , противоположное событию , противоположное событию  , происходит тогда и только тогда, когда событие , происходит тогда и только тогда, когда событие  не происходит. Другими словами, наступление события не происходит. Другими словами, наступление события  означает просто то, что событие означает просто то, что событие  не наступило. не наступило. |
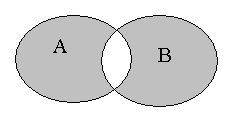  | Симметрическая разность двух событий  и и  (обозначается (обозначается  ) называется событие, состоящее из исходов, входящих в ) называется событие, состоящее из исходов, входящих в  или или  , но не входящих в , но не входящих в  и в и в  одновременно. одновременно.Смысл события  состоит в том, что наступает одно и только одно из событий состоит в том, что наступает одно и только одно из событий или или  . . . .Обозначается симметрическая разность:  или или  . . |
Свойства операций над событиями
Поскольку случайные события рассматриваются как множества, определенные на пространстве элементарных исходов
 , очевидно, что алгебраические свойства случайных событий вытекают из соответствующих свойств множеств:
, очевидно, что алгебраические свойства случайных событий вытекают из соответствующих свойств множеств:| | |
Приведенный список не исчерпывает всех свойств операций над событиями. В то же время из него видно, что основные действия над событиями, в частности, операции сложения (объединения) и умножения (пересечения), в определенном смысле аналогичны сложению и умножению чисел. Эти операции обладают свойствами коммутативности, ассоциативности и дистрибутивности. Для операции умножения событий роль, аналогичную роли единицы и нуля при умножении чисел, выполняют, соответственно, множества
 и
и  . Вместе с тем, теоретико–множественные равенства 6, 6 и им подобные показывают, что полной аналогии нет.
. Вместе с тем, теоретико–множественные равенства 6, 6 и им подобные показывают, что полной аналогии нет.Алгебра и сигма-алгебра событий
В случае конечной или счетной теоретико-вероятностной схемы в качестве события рассматривается любое подмножество конечного или счетного пространства элементарных событий
 . Если же пространство
. Если же пространство  непрерывно, то имеет место континуум элементарных исходов. Попытка считать событием любое подмножество непрерывного пространства
непрерывно, то имеет место континуум элементарных исходов. Попытка считать событием любое подмножество непрерывного пространства  сопряжена с большими трудностями.
сопряжена с большими трудностями.Поэтому в общем случае приходится иметь дело не со всеми подмножествами пространства
 , а лишь с определенным классом, замкнутым относительно операций суммы, произведения и дополнения.
, а лишь с определенным классом, замкнутым относительно операций суммы, произведения и дополнения.Предположим, что
 является пространством всех элементарных исходов для какого-нибудь случайного эксперимента, каждому результату которого соответствует ровно одна точка из
является пространством всех элементарных исходов для какого-нибудь случайного эксперимента, каждому результату которого соответствует ровно одна точка из  , а разным результатам соответствуют разные точки. Выделим некоторую совокупность
, а разным результатам соответствуют разные точки. Выделим некоторую совокупность  случайных событий
случайных событий  , определенных на пространстве элементарных исходов
, определенных на пространстве элементарных исходов  . Другими словами, выделим совокупность подмножеств
. Другими словами, выделим совокупность подмножеств  множества
множества  . Причем, наложим условие, что
. Причем, наложим условие, что  содержит как случайные события
содержит как случайные события  , так и события, полученные в результате применения любой из описанных операций к любым элементам системы.
, так и события, полученные в результате применения любой из описанных операций к любым элементам системы.Совокупность
 случайных событий
случайных событий  , определенных на пространстве элементарных исходов
, определенных на пространстве элементарных исходов  , называется алгеброй или булевой алгеброй – по имени английского математика Дж. Буля (1815 – 1864), если выполнены следующие условия:
, называется алгеброй или булевой алгеброй – по имени английского математика Дж. Буля (1815 – 1864), если выполнены следующие условия:-
 (алгебра событий содержит достоверное событие);
(алгебра событий содержит достоверное событие);
- Если
 , то
, то  для любых
для любых  (вместе с любым конечным набором событий алгебра содержит и их сумму);
(вместе с любым конечным набором событий алгебра содержит и их сумму);
- Если
 , то
, то  (вместе с любым событием алгебра содержит противоположное событие).
(вместе с любым событием алгебра содержит противоположное событие).
Можно показать, в частности, что:
 , если
, если  и
и  , то:
, то:-
 ;
;
-
 .
.
Другими словами, оказывается, что условий 1 – 3 достаточно для того, чтобы любое конечное число других операций над случайными событиями
 не выводило бы нас за пределы алгебры
не выводило бы нас за пределы алгебры  . Таким образом, алгебра множеств – это система подмножеств некоторого множества
. Таким образом, алгебра множеств – это система подмножеств некоторого множества  , замкнутая относительно операций суммы (объединения), произведения (пересечения) и дополнения.
, замкнутая относительно операций суммы (объединения), произведения (пересечения) и дополнения.Очевидно, что одно и то же множество
 порождает различные алгебры. Самая «бедная» алгебра состоит из двух множеств – пустого множества и множества
порождает различные алгебры. Самая «бедная» алгебра состоит из двух множеств – пустого множества и множества  :
: .
.В понятиях теории вероятностей это соответствует невозможному и достоверному событиям. Любое подмножество
 порождает четырехэлементную алгебру:
порождает четырехэлементную алгебру:
Для экспериментов с конечным числом исходов множество–степень
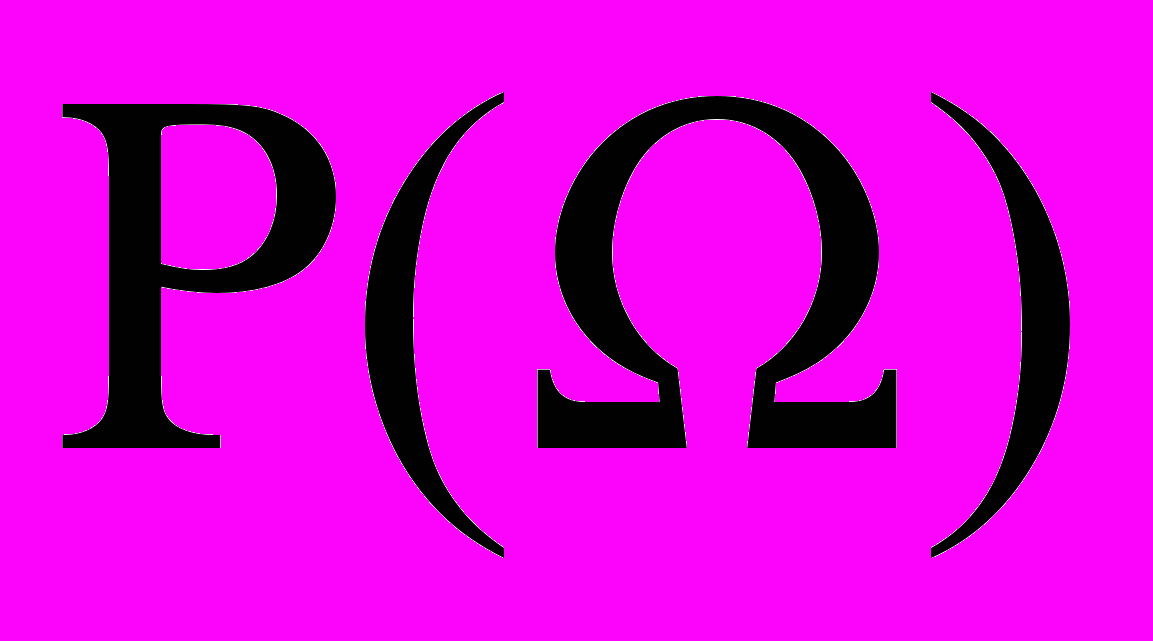 множества
множества  , т.е. совокупность всех подмножеств
, т.е. совокупность всех подмножеств  , включающая пустое множество , составляет алгебру
, включающая пустое множество , составляет алгебру 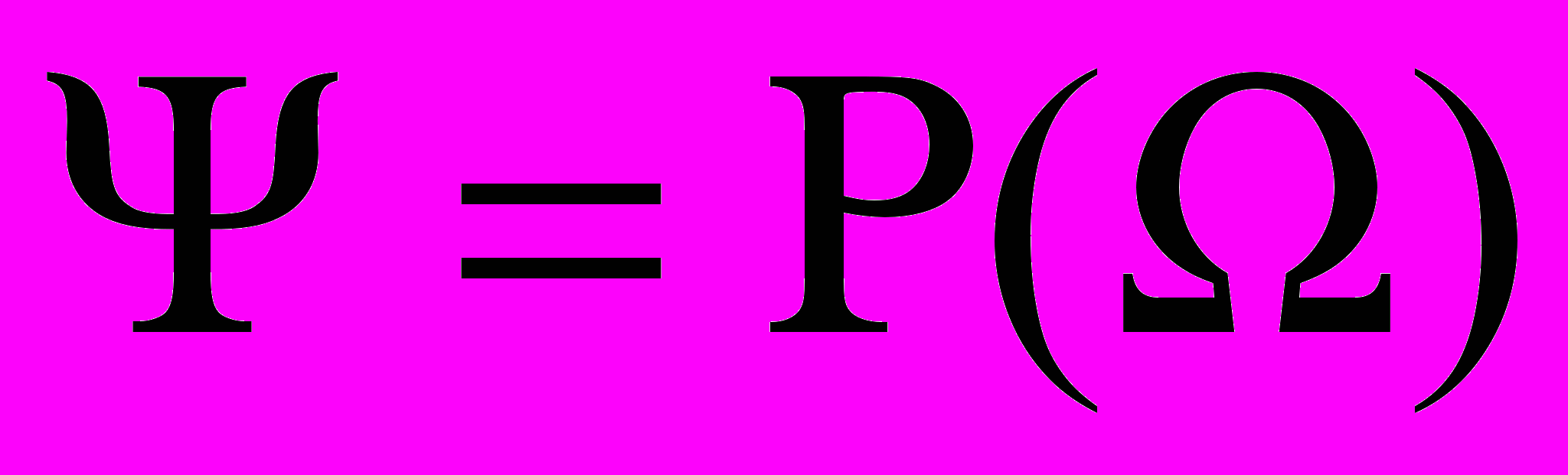 , причем это самая «богатая» алгебра, порождаемая множеством
, причем это самая «богатая» алгебра, порождаемая множеством  . Поэтому для таких экспериментов любое подмножество множества
. Поэтому для таких экспериментов любое подмножество множества  может интерпретироваться как наблюдаемое событие, а все события, связанные с пространством элементарных исходов
может интерпретироваться как наблюдаемое событие, а все события, связанные с пространством элементарных исходов  , образуют алгебру наблюдаемых случайных событий.
, образуют алгебру наблюдаемых случайных событий.Под наблюдаемым событием понимается такое подмножество множества
 , которое одновременно принадлежит и булевой алгебре
, которое одновременно принадлежит и булевой алгебре  . Таким образом, класс наблюдаемых в данном эксперименте событий, вообще говоря, ỳже класса всех подмножеств множества
. Таким образом, класс наблюдаемых в данном эксперименте событий, вообще говоря, ỳже класса всех подмножеств множества  . Если, например,
. Если, например,  , но
, но  , то событие
, то событие  по определению не наблюдаемо в данном эксперименте. Такое определение наблюдаемого события согласуется с введенным ранее эмпирическим понятием случайного события, как наблюдаемого результата эксперимента.
по определению не наблюдаемо в данном эксперименте. Такое определение наблюдаемого события согласуется с введенным ранее эмпирическим понятием случайного события, как наблюдаемого результата эксперимента.При рассмотрении многих задач теории вероятностей приходится иметь дело и с бесконечным числом операций. Для того, чтобы можно было рассматривать бесконечное число операций над событиями, необходимо усилить ограничения, налагаемые на алгебру
 .
.Система подмножеств
 множества , называется -алгеброй, а соответствующее множество событий борелевским, если она удовлетворяет следующим условиям:
множества , называется -алгеброй, а соответствующее множество событий борелевским, если она удовлетворяет следующим условиям:-
 (–алгебра событий содержит достоверное событие);
(–алгебра событий содержит достоверное событие);
- Если
 , то для любых
, то для любых 
 (вместе с любым конечным или счетным набором событий –алгебра содержит и их сумму);
(вместе с любым конечным или счетным набором событий –алгебра содержит и их сумму);
- Если
 , то
, то  (вместе с любым событием –алгебра содержит противоположное событие).
(вместе с любым событием –алгебра содержит противоположное событие).
Условие 2 для алгебры
 является следствием условия 2 для –алгебры, поэтому требования для –алгебры более сильные.
является следствием условия 2 для –алгебры, поэтому требования для –алгебры более сильные.Используя условие 3 и равенство
 , легко убедиться в справедливости следующего утверждения.
, легко убедиться в справедливости следующего утверждения.Пусть
 – –алгебра. Тогда, если
– –алгебра. Тогда, если  , то для любых
, то для любых 
 .
.Таким образом, счетное число операций суммирования или перемножения событий не выводит за пределы –алгебры.
Вообще говоря, действия над событиями важны не сами по себе, а как средство определения вероятностей одних событий через вероятности других событий. Далее будет введена вероятность случайного события как функция, заданная на подмножествах пространства
 . Прежде, чем определять эту функцию, следует задать область определения этой функции. Поскольку эта функция задается для всех наблюдаемых событий, связанных с пространством элементарных исходов
. Прежде, чем определять эту функцию, следует задать область определения этой функции. Поскольку эта функция задается для всех наблюдаемых событий, связанных с пространством элементарных исходов  , то функция должна быть определена на системе подмножеств
, то функция должна быть определена на системе подмножеств  пространства
пространства  , которая является –алгеброй. Поэтому разумно поставить следующее условие: если известны вероятности событий
, которая является –алгеброй. Поэтому разумно поставить следующее условие: если известны вероятности событий  и
и  , то должны быть определены правила вычисления вероятностей событий
, то должны быть определены правила вычисления вероятностей событий  ,
,  , а также вероятности противоположных событий
, а также вероятности противоположных событий  и
и  .
.























