Бобир С. Л., Боровик А. Г., Гетта В. Г., Гринь Т. В., Жила С. О., Завацька Л. М., Зайченко І. В., Іванишина В. П., Носко М. О., Сидоренко В. К., Кузьомко Л. М., Ляшенко О

Вид материала

Документы

Содержание Використані джерела Method of projects in educational process Професійне становлення фахівця із соціальної роботи Ключові слова Key words

Подобный материал:

• Бобир С. Л., Боровик А. Г., Гетта В. Г., Гринь Т. В., Жила С. О., Завацька Л. М., Зайченко, 7100.22kb.
• Основы безопасности жизнедеятельности (обж) М. С. Сидоренко,, 1983.12kb.
• Я україни буковинська державна медична академія в. А. Троянський, М. М. Сидоренко, 2652.9kb.
• Г. Г. Файзуллин // Экономика с Х. и перераб предприятий. 2011. № С. 65-67, 248.06kb.
• Т. А. Боровик Инновационные технологии развития музыкальности детей на урок, 22.38kb.
• Сидоренко Александр Михайлович Сидоренко вологодский писатель и поэт. Он оставил знатокам, 48.46kb.
• 19. 00 Малый зал Филармонии галина сидоренко, 80.16kb.
• Положення, 84.19kb.
• Театрально-концертне життя, 82.63kb.
• 1. Зайченко А. Крестьянскому подворью- государственную поддержку // апк: экономика,, 20.47kb.

Використані джерела

1. Генкал С.Е. організація самостійної пізнавальної діяльності учнів профільних класів на основі індивідуальних освітніх проектів: дис. … канд. пед. наук: 13.00.09 / Світлана Едуардівна Генкал. – Суми, 2008. – 226 с.
   
2. Коломієць А.М. Теоретичні та методичні основи формування інформаційної культури майбутнього вчителя початкових класів: дис. … доктора пед. наук: 13.00.04 / Алла Миколаївна Коломієць. – Вінниця, 2008. – 526 с.
   
3. Малицька І.Д. Історико-педагогічні умови розвитку освітніх мереж у контексті створення інформаційного середовища (досвід країн Європи). [Електронний ресурс] / І.Д. Малицька – Режим доступу: gov.ua/ ejournals/ITZN/em1/content/06midcie.phpl.
   
4. Морзе Н.В. Система методичної підготовки майбутніх вчителів інформатики в педагогічних університетах: дис. … доктора пед. наук: 13.00.02 / Наталія Вікторівна Морзе. – К., 2003. – 605 с.
   
5. Осадчий В.В. Педагогічні засади професійного консультування молоді засобами Інтернет: дис. … канд. пед. наук: 13.00.04 / Вячеслав Володимирович Осадчий. – К., 2005. – 242 с.
   
6. Полат Е.С. Типология телекоммуникационных проектов / Е.С. Полат // Наука и школа.  1997.  №4. С. 5360.
   

Penkovets E.

METHOD OF PROJECTS IN EDUCATIONAL PROCESS

In these materials which is illumination of structure and terms use of method of projects in an educational process are presented in the articles.

Key words: method of projects, research project, creative project, practically-oriented project, acquainting-oriented project, telecommunications.

Надійшла до редакції 08.10.2010

УДК 331.102.24:37.032:364

Тополь О.І.

ПРОФЕСІЙНЕ СТАНОВЛЕННЯ ФАХІВЦЯ ІЗ СОЦІАЛЬНОЇ РОБОТИ

В статті розглянуті аспекти професійного становлення фахівця із соціальної роботи; зазначені професійні ролі та функції, зміст професійної діяльності; визначені вихідні цінності та мотивації, необхідні знання, уміння, особистісні якості, критерії та компоненти професіоналізму фахівця із соціальної роботи.

Ключові слова: фахівець із соціальної роботи, професіоналізм, кваліфікаційні вимоги, професійна компетентність, професійні якості, професійне становлення, професійна самосвідомість.

Специфіка сучасної соціальної роботи вимагає високого рівня професіоналізму. Професіоналізм конкретного працівника є результатом його самореалізації в ході тривалого процесу професійного становлення, для якого характерні індивідуальна своєрідність й унікальність умов протікання. Професійне становлення фахівця із соціальної роботи – цілісний і безперервний процес розвитку практичної, освітньої й дослідницької діяльності особистості у соціальній сфері, орієнтований на формування професійних знань, умінь, навичок і особистісних якостей, адекватних кваліфікаційним вимогам та етичному стандарту професії.

Проблема професійного становлення і компетентності фахівця широко обговорюється у науково-професійній літературі. Методологічні й теоретичні аспекти розвитку професійної компетентності розглянуті в роботах С. Харченко, В. Докучаєвої, Н. Краснової, Н. Ларіонової, Д. Разіної, Е. Зєєра, А. Маркової та інших авторів. Формуванню професійної компетентності соціального працівника присвячені дослідження вітчизняних і зарубіжних учених, зокрема, А. Белінської, В. Бочарової, В. Сидорова, І. Ляшенка, І. Миговича, Г. Попович, Є. Холостової та інших.

У довіднику кваліфікаційних характеристик професій працівників, що надають соціальні послуги (затвердженому Наказом Міністерства праці та соціальної політики України від 14.10.2005 № 324) наводиться опис посадових обов’язків та кваліфікаційних вимог до керівників (директорів центрів соціального обслуговування, соціальної реабілітації інвалідів, центру підвищення кваліфікації працівників, інтернатів та ін.); професіоналів – «фахівця із соціальної роботи»; фахівців – «соціального працівника»; робітників – «соціального робітника».

Згідно кваліфікаційної характеристики фахівця із соціальної роботи, до його посадових обов'язків належать: організація виявлення та реєстрації громадян, які потребують соціальної та іншої допомоги, охорони і захисту їх морального, фізичного та психологічного здоров'я; організація піклування, опікування та догляду; встановлення причини конфліктних ситуацій та відхилень, які спричинили асоціальні явища; координація роботи з надання соціальної допомоги та захисту; пропаганда здорового способу життя, дбайливого ставлення до ветеранів та інвалідів, високих зразків етики та культури соціальних відносин; надання допомоги у працевлаштуванні; реєстрація асоціальних явищ і розробка заходів щодо їх усунення; проведення психологічних та педагогічних консультацій, надання юридичних порад; організація допомоги громадянам похилого віку й непрацездатним, тощо [1, 34-35].

Фахівець із соціальної роботи повинен знати: законодавство України, нормативно-правові акти, методичні та інші розпорядчі документи та матеріали, які регламентують організацію соціальної роботи; організацію соціально-медичної роботи; організацію юридичної допомоги, піклування, опікування, догляду, соціальної реабілітації, соціального захисту; соціологію; психологію; технології соціальної роботи; національні особливості побуту, культуру людських відносин та інше. Кваліфікаційними вимогами до фахівця із соціальної роботи є повна вища освіта відповідного напряму підготовки (магістр, спеціаліст) та підвищення кваліфікації.

Професійні обов'язки фахівця із соціальної роботи обумовлюють його ролі. Він виступає як соціальний педагог, учитель, вихователь, експерт, консультант, коли надає поради, навчає різним умінням, ефективним методам родинного планування і господарювання, встановлює зворотній зв'язок, застосовує рольові ігри та інше. Фахівець виступає в ролі посередника, організатора, адміністратора, коли його діяльність спрямована на допомогу у подоланні проблем особи, що знаходиться у важкій життєвій ситуації. Він виступає в ролі соціального адвоката, коли представляє інтереси клієнта або групи клієнтів, наприклад при встановленні або позбавленні батьківських прав, опікунства, тощо.

Ф
© Тополь О.І., 2010
ахівець виконує свої ролі, працюючи в соціальних службах установ, підприємств і організацій різних відомств, в освітніх, культурних і медичних установах, будинках, мікрорайонах або зонах соціального обслуговування сімей, а також займаючись приватною практикою. Дії фахівця в його професійних ролях представляють сукупність конкретних операцій, необхідних для реалізації цілого ряду професійних функцій.


За змістом діяльності фахівця соціальної роботи виділяють такі функції [3, 24-26; 4, 30]:

• організаційну (організація соціальних служб, залучення до їх роботи громадськості та спрямування діяльності на надання різних видів допомоги і соціальних послуг);
  
• посередницьку (забезпечення сприяння й участі в рішенні проблеми органів влади та інших соціальних установ);
  
• правозахисну (використання законів та їх правових актів для захисту прав клієнта і надання йому допомоги);
  
• інформаційну (забезпечення нужденних у соціальній допомозі інформацією про соціальні послуги);
  
• психологічну, педагогічну, соціально-медичну, соціально-побутову (виявлення необхідності та сприяння в наданні відповідної допомоги різним категоріям населення) та інші.
  

За використовуваними технологіями виділяють наступні функції:

• діагностичну (постановка соціального діагнозу, визначення змісту проблеми групи або індивіда);
  
• прогностичну (прогнозування розвитку соціальних процесів і вироблення моделей соціальної поведінки);
  
• профілактичну (приведення в дію механізмів попередження негативних соціальних явищ);
  
• реабілітаційну (організація роботи із соціальної адаптації та реабілітації) та інші.
  

Виконуючи різні професійні ролі та функції, фахівець виробляє особливий стиль поведінки, систему власної унікальної діяльності з надання соціальної допомоги й підтримки клієнта.

Велике значення для успішної професіоналізації має спрямованість фахівця із соціальної роботи, яка складається із системи цінностей та мотивації його діяльності. Вона обумовлює професійну придатність до практичної соціальної роботи. Цінності – це ідеї, переконання на які фахівець спирається при прийнятті рішень. Розрізняють цінності альтруїстичного характеру (допомога, підтримка, захист), цінності етичної відповідальності (гідність і цілісність професії) та цінності, пов’язані з потребами самореалізації, самоствердження, самовдосконалення і досягнення професіоналізму [2, 245].

Головним внутрішнім стимулом праці в соціальній сфері є альтруїстична мотивація – бажання фахівців із соціальної роботи приносити користь своїм клієнтам і суспільству. Також до значимих внутрішніх стимулів відносять можливість постійного прояву самостійності, ініціативи і творчості в роботі. До зовнішніх стимулів належить суспільне визнання важливості професії соціального працівника, усвідомлення необхідності її здійснення для підвищення соціального здоров'я і благополуччя громадян, прояв поваги з боку оточуючих.

Стиль поведінки, професійна компетентність фахівця із соціальної роботи обумовлені сукупністю його професійних знань, умінь, навичок; комплексом психологічних особливостей та професійно важливих якостей та здібностей. Здатність досягати найвищих успіхів в професійній діяльності багато в чому залежить від самооціночних здібностей (самоконтроль, самовдосконалення, самоосвіта).

Фахівець повинен бути психологічно готовим до діяльності в соціальній сфері, мати сформоване професійне мислення, вміти самостійно аналізувати конкретну ситуацію, оцінювати можливі наслідки та брати відповідальність за обрані рішення, які часто пов’язані з життям людини.

Професійно важливі психологічні якості:

1. психічні: особливості психічних процесів (пам’яті, мислення, сприймання, відчуття, уяви); увага, як стан свідомості та умова виконання діяльності; психічні стани (працездатність, енергійність, ініціативність, стресостійкість, низький рівень тривожності); емоційно-вольові прояви (стриманість, наполегливість, послідовність, імпульсивність та ін.
   
2. інтелектуальні: соціальний інтелект (здатність аналізувати стани інших людей, передбачати розвиток подій); творче мислення (здатність приймати нестандартні рішення, діяти у невизначених ситуаціях); аналітичність, реалістичність, інтуїтивність, прогностичність, критичність, гнучкість мислення; ерудиція та кругозір; достатній освітній рівень та ін.;
   
3. професійна самосвідомість: самоконтроль, самокритичність, адекватна самооцінка, прагнення до самовдосконалення й самоосвіти, самонавіюваність, уміння керувати власними емоціями та поведінкою, змінювати власні стани.
   

Професійно важливі морально-етичні та вольові якості:

• емпатійність (здатність до співчуття, співпереживання, відчуття настрою людини, розуміння її внутрішнього світу);
  
• делікатність, тактовність, уважність до клієнта (звернення уваги на настрій клієнта, його самопочуття, дотримання принципу «не зашкодь»);
  
• терпимість (повага до інтересів, переконань, ідеалів, потреб, звичок інших людей, сприймання людини такою якою вона є, з її правом на обраний спосіб життя);
  
• витримка і терплячість (контроль над власними емоціями на виклики роздратованості, агресивності та ін.);
  
• висока духовна культура й моральність, етична поведінка, гуманність, милосердя, чуйність, безкорисливість (спрямованість на інтереси, потреби і захист людської гідності клієнта, бажання допомогти, симпатія до інших);
  
• чесність (правдивість у поясненні становища клієнта, можливостей вирішення його проблем, можливих труднощів);
  
• об’єктивність та справедливість (рівне ставлення до клієнта, не зважаючи на власні симпатії, адекватне оцінювання його проблем);
  
• моральна чистота в професійних справах, конфіденційність (уміння зберігати таємницю, якщо вона не несе загрозу іншим людям);
  
• порядність, відповідальність (моральна відповідальність за свою поведінку і наслідки власних дій);
  
• емоційно-позитивне ставлення до людей: доброзичливість, доброта, любов до людей, оптимізм (уміння сприймати людину як самоцінність, формувати позитивні почуття до неї, вселяти надію на краще);
  

Професійно-операційні якості та здібності:

1. професійні знання: теоретичні (з психології, педагогіки, соціології, медицини, права, геронтології та ін.) та практичні (володіння технологіями соціальної роботи), уміння застосовувати теоретичні знання на практиці, навички роботи з різними категоріями клієнтів, що знаходяться в різних умовах і ситуаціях;
   
2. організаторсько-комунікативні здібності: уміння швидко встановлювати контакт з людьми, виявляти їх установки, очікування; атрактивність (привабливість особистості, уміння вислухати клієнта та спрямувати бесіду в конструктивне русло); уміння викликати симпатію і довіру співрозмовника й створювати сприятливу атмосферу у взаємовідносинах з ним; красномовство (уміння впливати і переконувати).
   

Сукупність особистісних якостей, що змінюються в процесі професійного становлення, утворюють комплекс професійних здатностей фахівця із соціальної роботи, які виступають операційними механізмами рішення проблем клієнтів.

Нормою регулювання професійної діяльності та результатом самореалізації особистості в цій діяльності виступає професіоналізм, що характеризується стійким рівнем знань, умінь і навичок, який дозволяє досягати ефективності й успіху. Професіоналізм фахівця із соціальної роботи включає: здатність аналізувати ситуацію, правильно її сприймати, брати до уваги всі існуючі альтернативи та робити необхідний вибір; уміння встановлювати контакт з людьми, здійснювати диференційований підхід до клієнтів; здібність управляти діяльністю соціальної служби, використовувати в соціальної роботі технології проектування, моделювання та інші.

Серед компонентів професіоналізму особливе значення має його комунікативна складова. Оскільки різноманіття форм взаємодії в соціальній роботі проявляє себе через численні форм соціальної комунікації, вона пронизує всі сторони професійної діяльності фахівця. Через комунікативні акти встановлюється контакт та вибудовується система відносин з клієнтом, відбувається спілкування, здійснюється розуміння й пізнання його проблем.

Соціальна комунікація – це двосторонній процес обміну інформацією та спосіб дії в суспільстві, що веде до взаєморозуміння його учасників. Розрізняють три основні моделі соціальної комунікації: лінійну, за якої комунікант (хто передає інформацію або повідомлення) активно діє, а реципієнт (кому передається інформація) пасивно сприймає цю дію; інтерактивну, за якої встановлюється зворотний зв'язок між комунікантом і реципієнтом, що дозволяє їм краще адаптуватися один до одного; трансакційну, що характеризується активною взаємодією з постійно діючим зворотним зв'язком.

У соціальній роботі використання інтерактивної та трансакційної моделей комунікації пов'язане з реалізацією ідеї соціального партнерства. Клієнт як об’єкт та суб'єкт соціальної роботи повинен брати активну участь в процесі вирішення власної проблеми, співпрацюючи з фахівцем. Умовою ефективного спілкування із клієнтом є якісно-оптимальний рівень взаємодій з ним. Високий рівень професійного спілкування вимагає використання цілого комплексу знань, навичок й умінь. Вони стосуються організаційно-управлінського компоненту комунікації (уміння контролювати хід і результат спілкування); її когнітивного компоненту (уміння використати інструментарій спілкування); емоційно-особистісного компоненту (уміння проявляти емпатію в процесі спілкування).

Спілкування виражається у взаєминах наступних типів [5, 206]:

1) «Я – Я» (індивідуально-особистісний тип спілкування);

2) «Я – Ми» (індивідуально-колективний тип);

3) «Ми – Ми» (колективно-суспільний тип).

Соціальний працівник повинен уміти вислухати й зрозуміти, пояснити й довести, запитати й відповісти, переконати, створити атмосферу довіри в бесіді, знайти індивідуальний психологічний підхід до клієнта, розв'язати конфлікт, зняти напругу. В основі такої діяльності лежить комунікативна техніка спілкування, володіння якою є важливою ознакою професійної придатності фахівця із соціальної роботи. Характеристики, що складають професійний портрет фахівця з погляду володіння ним комунікативною технікою, називають комунікативною професіограмою.

Фахівець із соціальної роботи повинен:

• знати мовний етикет і вміти його використати;
  
• уміти формулювати цілі і завдання ділового спілкування;
  
• організовувати спілкування й управляти ним;
  
• аналізувати предмет спілкування, розбирати скаргу, заяву, ставити питання й конкретно відповідати на них;
  
• володіти навичками й прийомами ділового спілкування, його тактикою й стратегією;
  
• уміти вести бесіду, співбесіду, ділову розмову, диспут, полеміку, дискусію, діалог, дебати, круглий стіл, ділову нараду, ділову гру;
  
• мати навички доводити й обґрунтовувати, аргументувати й переконувати, критикувати й спростовувати, досягати угод і рішень, компромісів і конвенцій, робити оцінки й пропозиції;
  
• володіти технікою мовлення, риторичними прийомами й фігурами, уміти правильно будувати промову й інші публічні виступи;
  
• уміти за допомогою слова проводити психотерапію, знімати стрес, страх, адаптувати клієнта до відповідних умов, коректувати його поведінку й оцінки.
  

Таким чином, завдання фахівця із соціальної роботи полягає у тому, щоб допомогти клієнтові знайти себе, знайти своє місце в динамічно мінливому світі, зорієнтуватися в нових соціальних відносинах, і спілкування є важливим інструментом у цьому процесі.

Фахівець із соціальної роботи повинен мати навички саморегуляції, самоорганізації (уміти опановувати свої думками, почуття, поведінку, проводити самоспостереження), що є основою самовдосконалення й професійного росту. В особливих, важких або екстремальних умовах діяльності, коли зовнішні або внутрішні фактори викликають порушення нормальної діяльності функціональних систем, виникає природна потреба відновити рівновагу, збалансованість психічних процесів. У результаті усвідомлення ситуації з’являється мотив тієї або іншої дії з метою пристосування до нестандартної обстановки, відбувається активізація системи психічної саморегуляції, виникає потреба «зібратися», «мобілізуватися», «перебудуватися». Це характерно для початку рефлексії, коли найчастіше запускається механізм самоаналізу й самооцінки, вироблення й прийняття рішень.

Отже, професійне становлення – це продуктивний процес розвитку і саморозвитку особистості, освоєння та самопроектування професійно орієнтованих видів діяльності, визначення свого місця у світі професій, реалізація себе в професії й самоактуалізація свого потенціалу для досягнення вершин професіоналізму.

Дієвість професійного становлення фахівця із соціальної роботи залежить від наступних умов: психологічної відповідності вимогам професії; спрямованості на діяльність у соціальній сфері (наявність стійкого інтересу і схильності до професії); змісту й технологій професійно-освітнього процесу в навчальному закладі та інших

Професійна самосвідомість є провідним чинником, який зумовлює професіоналізація майбутніх фахівців із соціальної роботи. На початкових стадіях професійного становлення вирішальне значення мають протиріччя між особистістю й зовнішніми умовами життєдіяльності. На стадіях професіоналізації й особливо професійної майстерності провідного значення набувають протиріччя внутрісуб'єктного характеру, що обумовлені внутріособистісними конфліктами, незадоволенням своїм професійним рівнем, потребою у саморозвитку, самоздійсненні, професійному зростанні. Розв’язання цих протиріч приводить до знаходження нових способів виконання професійної діяльності й, відповідно, підвищення професійного рівня.

Використані джерела

1. Довідник кваліфікаційних характеристик професій працівників / М-во праці та соц. політики України. Вип. 80: Соціальні послуги – Краматорськ: Центр продуктивності, 2005. – 74 с.
   
2. Основы социально работы: Учебник / Отв. ред. П. Д. Павленок. – М. : ИНФРА, 2001. – 395 с.
   
3. Соціальна роботи: технологічний аспект: Навчальний посібник / За ред. А. Й. Капської. – К. : Центр навчальної літератури, 2004. – 352 с.
   
4. Филатова Е. В. Теория социальной работы: Учебное пособие / Е. В. Филатова. – Кемерово: Кузбассвузиздат, 2004. – 96 с.
   
5. Фирсов М. В. Теория социальной работы: Учебное пособие для студентов. высш. учеб. Заведений / М. В. Фирсов, Е. Г. Студенова. – М. : ВЛАДОС, 2001. – 432 с.
   

Topol O.

professional becoming of social work specialist

The aspects of the professional becoming of social work specialist are considered in the article; professional roles and functions, content of professional activity are noted; values and motivations, necessary knowledges, abilities, personality qualities, criteria and the component of social work specialist’s professionalism are determinate.

Key words: social work specialist, professionalism, qualifying requirements, professional competence, professional qualities, professional becoming, professional consciousness.

Надійшла до редакції 12.04.2010

УДК 001

Кілочицька Т.В.

Використання матеріалу історії науки при викладанні
вищої математики

У зв’язку з гуманізацією освіти розглядається доцільність використання елементів історизму при викладанні вищої математики, наведені приклади.

Ключові слова: гуманізація освіти, історія математики, математичні поняття.

Одна з провідних тенденцій розвитку сучасної освіти є її гуманізація та гуманітаризація. Ця тенденція зумовлена соціальним запитом, адже в наш час необхідно постійно стимулювати мислення студента, спонукати його до вироблення власної життєвої позиції.

Так, гуманізація освіти полягає в тому, щоб навчання було доступним і цікавим. Доступність та інтерес до нової інформації – дві основні складові гуманізації освіти. Ще у філософії Цицерона, Юстина Філософа містяться погляди на людину як найвищу цінність та її вільний розвиток з урахуванням досягнень освіти, античної культури. Вперше ж застосував поняття гуманізації щодо педагогічної науки французький філософ і педагог Жан-Жак Руссо в теорії вільного виховання. В основі цієї теорії лежить ставлення до людини як до самоцінної особистості.

Практичним втіленням гуманізму в освіті стали положення гуманістичної педагогіки – напряму в теорії і практиці виховання, який виник усередині XX ст. в США. Його пріоритетним завданням є сприяння максимальній реалізації можливостей особистості, яка прагне до сприймання нового досвіду і здатна до усвідомленого і самостійного вибору в різних життєвих ситуаціях.

Ідеї гуманізму становили основу побудови педагогічних систем, обстоювалися як принципи розбудови гуманної педагогіки, пов'язані з іменами Я.А. Коменського, Ж.-Ж. Руссо, Д. Локка, І.Г. Песталоцці, К.Д. Ушинського, а пізніше – С.Т. Шацького, А.С. Макаренка, В.О. Сухомлинського, Г.Сковороди, Л. Толстого, Я. Корчака [1, 2, 3, 4, 5]. Певний вплив на запровадження гуманістично орієнтованого навчання мали праці психологів, зокрема Абрахама Маслоу, Карла Роджерса [6, 7, 8].

Зрозуміло, що кожна професійна діяльність потребує від спеціаліста певних якостей і здібностей. Тому важливим є також адекватний вибір професії у відповідності з нахилами і здібностями людини. Якщо ж казати про гармонійний розвиток особистості, то математика займає не останнє місце. Розгляд математики повинен відбуватися не лише як засобу науково-технічного прогресу, що зміцнює матеріальний потенціал суспільства, але і як потужний засіб духовного зростання. Використання елементів історизму при викладанні вищої математики сприяє більш гуманітарному спрямуванню математичної освіти.

Недостатня математична освіта, низька математична культура ХХІ ст. можуть стати серйозною перешкодою на шляху до формування професійних якостей майбутнього випускника вищого навчального закладу. В наш час відбувається постійне скорочення годин, виділених на вивчення математики, збільшується розрив між рівнем математичних знань випускників ВНЗ і об’єктивними потребами сучасної науки і техніки, існує певна невідповідність шкільного курсу математики з вимогами до знань студентів у вищій школі. Для того, щоб вирішити останню проблему треба удосконалювати методику викладання математики, використовувати у навчанні інформаційні технології, зокрема при вивченні таких розділів як теорія ймовірностей та математична статистика.

На першому занятті з вищої математики доцільно провести 5-10 хвилинне тестування для виявлення рівня підготовки студентів. На лекціях слід використовувати елементи наочності: графіки, логічні схеми, таблиці (об’єм сприйняття – 5-7 об’єктів на таблиці). Доцільно використовувати контекстне навчання (мотивація до засвоєння знання досягається розв’язуванням практичних задач), міждисциплі­нарний підхід до навчання, навчання на основі аналізу реальних життєвих ситуацій. Цього можна досягти введенням елементів історизму в навчальні дисципліни. Адже, чим вище рівень розвитку мислення і творча активність студента, тим вище рівень сформованості його особистих та професійних якостей.

Однією з проблем у викладанні вищої математики є велике навантаження навчальної програми. Наприклад в першому семестрі 1 курсу студенти вивчають такі розділи математики: лінійна алгебра, векторна алгебра, алгебра і теорія чисел, аналітична геометрія, вступ до математичного аналізу, диференціальне числення функції однієї змінної. З метою мотивації навчання і для більш швидкого і тривалого запам’ятовування у студентів слід більшість математичних понять вводити за допомогою історичних геометричних чи фізичних задач з обов’язковим застосуванням, наприклад в техніці (для технічних спеціалізацій). Крім того, у викладанні курсу вищої математики повинні бути присутні короткі відомості про історію окремих розділів математики в контексті розвитку світової науки з обов’язковим висвітленням основних надбань української науки.

З
© Кілочицька Т.В., 2010
араз мною проводиться робота по створенню курсу лекцій, що дасть можливість студентам підготуватися самостійно до лекції, наперед ознайомитись з новим матеріалом лекції. При цьому ефективність самостійної роботи залежить від індивідуальних здібностей та особливостей психіки студента (уваги, пам’яті тощо) і це обов’язково треба враховувати. Навчання повинно орієнтуватися на максимально можливе врахування психофізичних особливостей студентів, що ґрунтується на якісній психолого-педагогічній діагностиці.

Введення елементів історії математики має метою:

• підвищення інтересу студентів до вивчення вищої математики, до наукової творчості;
  
• посилення міжпредметних зв’язків, гуманізації освіти;
  
• поглиблення розуміння нового матеріалу, розвиток критичного мислення;
  
• з’ясування ролі і місця математики в практичній діяльності людей різних історичних епох;
  
• визначення передумов створення нових математичних теорій, методів доведення теорем.
  

Виклад історичного матеріалу повинен бути продуманим і органічно переплітатися з викладом основного матеріалу навчального курсу, доповнювати і не заважати його вивченню.

Доцільно історичний матеріал викладати коротким історичним повідомленням (5-10 хв.). Такі повідомлення можуть бути:

• з історії окремого напряму математики (фрагменти текстів праць видатних математиків, історичні задачі);
  
• бібліографічні відомості про окремого видатного математика, який працював в даному науковому напрямі (використання імені вченого в процесі вивчення матеріалів лекцій, подання портрету вченого, виклад короткої бібліографічної довідки, висловлювання вчених про математику і математиків).
  

Ці історичні повідомлення обов’язково повинні бути органічно поєднані з новим матеріалом лекції. Так, короткі бібліографічні довідки про вчених доцільно викласти на початку лекції з метою мотивації і підвищення інтересу до навчання. Зокрема, при вивченні елементів алгебри слід пригадати Франсуа Вієта, юриста за освітою, який шляхом самоосвіти став батьком символічного числення. Він вперше став позначати буквами коефіцієнти рівнянь. Це дало можливість вивчати загальні властивості рівнянь і їх коренів.

При ознайомленні з історичним матеріалом треба обов’язково сказати студентам, що можна продовжувати наукове дослідження в цьому напрямі, узагальнити отримані результати. Це буде пробуджувати інтерес студентів до самостійного наукового дослідження, створюватиме перспективу у навчанні. Доцільно також акцентувати увагу на те, як вчений дійшов такого висновку, які методи використав при доведенні теореми.

При вивченні нових розділів вищої математики (теорії функцій багатьох змінних, теорії диференціальних рівнянь, теорії рядів, теорії ймовірностей і математичної статистики тощо) доцільно теж слідувати історичному підходу. Це створить умови для кращого розуміння і запам’ятовування нового матеріалу студентами, сприятиме формуванню у них математичної культури, усвідомленню логіки побудови математичних теорій.

В процесі подання історичного матеріалу (історична задача, теорема) слід створювати проблемну ситуацію. При введенні нового математичного поняття бажано розглянути еволюцію цього поняття, щоб воно не здалося студентам введеним штучно, без потреб практики.

Доцільно сказати, що становлення класичної науки, зокрема математичної, відбувалося в XVII ст. Швидко розвиваються диференціальне та інтегральне числення, теорія диференціальних та інтегральних рівнянь. Виникненню диференціального та інтегрального числення сприяли введення в математику змінної величини та методу координат, розвиток методів розв’язання задач на обчислення площ, об’ємів тіл, визначення центрів тяжіння, дотичних тощо. Зв'язок математики з механікою, астрономією, фізикою розширив уявлення про неперервні величини, функціональні залежності. Внесок у створення аналізу нескінченного малих належить в першу чергу вченим: І. Кеплеру, Г.Галілею, Б.Кавальєрі (учню Галілея), Е. Торричелі. У 1615 р. І. Кеплер застосовував метод сумування нескінченно малих, нестрогий метод обчислення об’ємів тіл обертання (тіло ділилось на частини, які переміщувались, утворюючи інше тіло, об’єм якого можна обчислити). Г. Галілей займався астрономією, технікою обчислень, конічними перерізами, тригонометрією [9, 10]. Зокрема, в книзі Б. Кавальєрі «Геометрія, викладена новим способом за допомогою неподільних неперервного» (1635) міститься ідея методу неподільних для визначення розмірів плоских фігур, вперше висловлена ним в 1621 р. Суть методу неподільних: якщо плоскі фігури або тіла відносяться один до одного, як всі їх неподільні разом, якщо всі неподільні знаходяться в одному відношенні один до одного, то відношення площ відповідних фігур або об’ємів тіл дорівнює цьому відношенню (по сучасному це відношення площин криволінійних трапецій і їх частин). Е.Торричеллі працював над розвитком методу Каварьєрі і вперше визначив об’єм тіла, утвореного обертанням вітки гіперболи навколо однієї з її осей. Метод Е. Торричеллі був незастосовний для визначення довжин кривих, бо відповідні неподільні точки залишалися без розміру. Крім того, нечітким було визначення поняття неподільного, не було введено нових символічних позначень. Б.Паскаль користувався методом Е.Торричеллі, причому суму всіх неподільних він розумів як суму елементарних площадок, утворених нескінченно близькими ординатами, обмеженими відрізком осі абсцис та кривої. Займалися дослідженнями в цьому напрямі вчені Валлис, Робенваль, П. Ферма, Р. Декарт, Барроу [11].

В творах І. Ньютона 1665-1666 рр. диференціальне і інтегральне числення розвивається у вигляді теорії флюксій, в творах Лейбніца 1682-1686 рр. як числення диференціалів [12]. Після зародження математичного аналізу механічні та фізичні задачі почали записуватись у вигляді диференціальних рівнянь. Постала задача розв’язання цих рівнянь. Виникненню інтегральних методів сприяли обернені задачі на дотичні, зокрема задача визначення кривих виходячи з загальної властивості всіх дотичних до них. Ця задача виникла з потреб практики, наприклад в мореплавстві, в геометричній оптиці, в кінематиці.

Якщо математичні поняття і твердження подавати студентам в історичному контексті, то вони будуть ефективніше, з розумінням історичного шляху їх виникнення сприйматися студентами.

Наприклад, поняття похідної виникло в XVII ст. при розв’язанні практичних задач визначення швидкості прямолінійного нерівномірного руху (вперше розв’язав І.Ньютон, 1662-1664) та побудови дотичної до кривої (в частинних випадках розв’язали Евклід в “Початках”, Р.Декарт в “Геометрії” (друга книга – метод нормалей), в загальному – Г. Лейбніц, 1684). Термін “похідна” вперше зустрічається в праці Луї Арбогаста “Обчислення похідних” (1800 р.). Цим терміном почали користуватися і інші вчені: Ж. Лагранж, О. Коші [13]. У 1823 р. О.Коші дав точне визначення похідної. Поняття ж диференціала вперше ввів Г. Лейбніц.

Щодо виникнення методів інтегрального та диференціального числення, то обернені задачі на дотичні розв’язувались наближеними графічними методами. Вперше зробив спробу створити загальний метод розв’язання таких задач Р. Декарт при розв’язанні задачі на дотичні де Бона. Ця задача як і інші обернені задачі вказувала на взаємооберненість задач про дотичні та інших. Суть цих задач полягала в розв’язуванні диференціальних рівнянь. Накопичення методів диференціального та інтегрального числення набуло явної форми у П. Ферма. У листі Р. Декарту 1638 р. він повідомив, що вирішив задачу визначення екстремуму функції.

Цікавий, вдало введений історичний матеріал з даної теми сприяє естетичному вихованню студентів.

Історичний підхід дозволяє врахувати напрям спеціалізації студентів.

При викладанні вищої математики доцільно також вказувати на роль наукових досліджень українських математиків та вихідців з України. Цінними для розвитку алгебри і геометрії є твори українського письменника, члена Кирило-Мефодіївського братства Миколи Івановича Гулака “Етюди про трансцендентні рівняння” (1852) та “Спроба геометрії чотирьох вимірів” (1877). Остання складається з двох частин: “Розмови про простір” та “синтетичної геометрії чотирьох вимірів” і є першою монографією з чотиривимірної евклідової геометрії в Російській імперії.

При вивченні теорії диференціальних рівнянь слід також вказати на подальший її розвиток, зокрема при дослідженні нелінійних коливань. Сказати, що вперше нелінійна задача з’являється в книзі І. Ньютона “Початки” (1687). Нелінійні рівняння досліджувалися М.В. Остроградським, К. Вейєршт­рассом, А. Ліндштедтом на іншими вченими XVIII – XІX ст. Наприкінці 20-х – початку 30-х рр. ХХ ст. радянські вчені Л.І. Мандельштам, О.О. Андронов, О.А. Вітт перенесли існуючі методи розв’язання нелінійних диференціальних рівнянь на дослідження коливальних процесів та розробили нові методи. Паралельно з їх дослідженнями на початку 30-х рр. ХХ ст. українські вчені Микола Митрофанович Крилов та Микола Миколайович Боголюбов започаткували нову галузь науки – нелінійну механіку [15, 16].

Можна дати студентам написати реферат про цих видатних вчених або коротко розповісти про цих видатних вчених. Творче життя вчених буде позитивним прикладом для студентів.

Зокрема, приклад наукової творчості українського вченого М.М. Боголюбова. Він після закінчення семирічної школи самостійно займався вивченням фізики та математики, з 1923 р. брав участь у семінарі Кафедри математичної фізики Київського університету під керівництвом академіка Д.О. Граве. На цей семінар прийшов М.М. Крилов і помітив математичні здібності виступаючого з доповіддю М.М. Боголю­бова. У п’ятнадцять років Микола Миколайович написав першу наукову працю з дослідження поведінки розв’язків лінійних диференціальних рівнянь на нескінченності (1924), в наступному році був прийнятий аспірантом Кафедри математичної фізики ВУАН. В 1928 р. він захистив працю “Про деякі нові методи у варіаційному численні” став працювати на Кафедрі математичної фізики ВУАН. В 1930 р. він одержав з варіа­ційного числення премію Болонської АН і загальними зборами фізико-математичного відділу ВУАН за поданням М.М. Крилова та Д.О. Граве йому була присуджена ступінь доктора математичних наук.

Ця доповідь на 5-10 хв. сприятиме виробленню життєвих пріоритетів студентів, мотивації навчання, гуманізації освіти.

Докладніше зупинимось на введені в лекційний матеріал елементів історії науки на прикладі вивчення окремих тем з теорії ймовірностей. Зокрема, при вивченні теми “Комбінаторика” слід студентам сказати, що окремі комбінаторні задачі з'явилися дуже давно. У відомих працях стародавніх індійських вчених знайдені формули числа перестановок і сполучень. В Європі елементи комбінаторики зустрічаються в працях Н. Тортальї (XVI ст.), але повної теорії перестановок, розміщень, сполучень він не дав. Перші теоретичні дослідження в цій галузі, у зв'язку з розвитком алгебри многочленів здійснили в XVII ст. французькі математики Б.Паскаль (1623-1662) і П.Ферма (1601-1665). Ряд комбінаторних задач розв'язав Л.Ейлер (1707-1783). Проте в справжню математичну науку комбінаторика перетворилася лише в XX ст., коли виникла потреба її застосування в обчислювальній техніці, кібернетиці, економіці та інших науках.

Зараз багато важливих проблем, пов'язаних з розробкою оптимальних планів виробництва, транспортування, розміщення підприємств зводиться до задач комбінаторного характеру. Ці задачі вимагають надзвичайно великої кількості варіантів, тому для швидшого їх розв’язання застосовують ЕОМ.

При вивченні незалежних випробувань, закону великих чисел слід пригадати Я. Бернуллі та С. Пуасона.

Я. Бернуллі (27.12.1654 – 16.08.1706) – відомий швейцарський математик. Народився у м. Базелі. Зробив багато відкриттів майже в усіх галузях математики, працював над розвитком аналізу нескінченно малих, варіаційного числення, теорії рядів і теорії ймовірностей. У праці “Мистецтво припущень” (1703) він розв’язав деякі задачі комбінаторики і, у зв’язку з визначенням суми виду 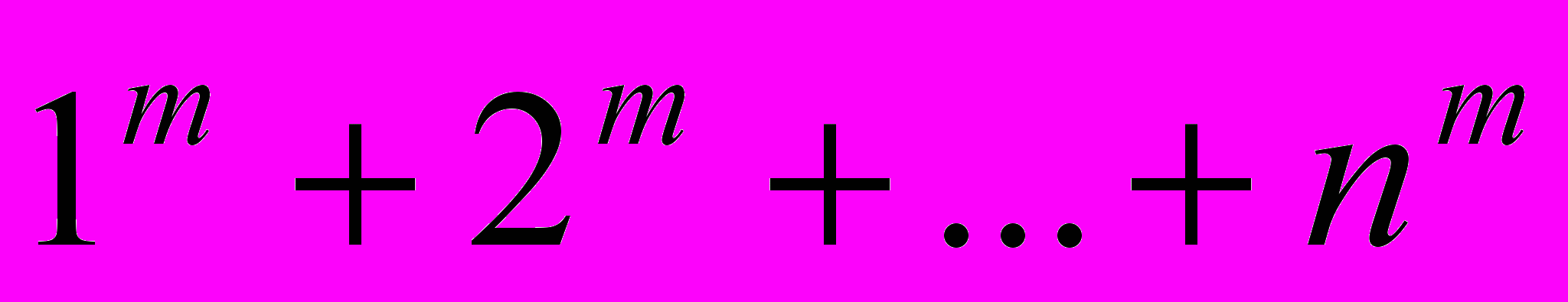, відкрив числа, які згодом було названо в його честь. У цій праці Я.Бернуллі довів так звану теорему Бернуллі – важливий окремий випадок закону великих чисел, що має велике значення в теорії ймовірностей.

С. Пуассон (21.06.1781 – 25.04.1840) – французький механік, фізик і математик, професор, член Паризької АН (з 1812 р.), почесний член Петербурзької АН (з 1826 р.). Народився в м. Піт’є. Батько сам навчав Сімеона, бажаючи підготувати його до діяльності нотаріуса, але, не виявивши в ньому здібностей до розумової праці, віддав у навчання до цирульника. Перша перукарська операція, яку виконав Пуассон, була дуже невдалою, що примусило його залишити і цю діяльність. Випадково Пуассон натрапив на задачі, вміщені в журналі Політехнічної школи, і розв’язав їх. Після цього батько і влаштував його в центральну школу Фонтенбло. Потім Сімеон вступив до політехнічної школи (1798 р.). Тут на його здібності звернули увагу Лаплас, Лагранж та інші професори. По закінченні курсу він був залишеним у цьому навчальному закладі. У 1816 р. його призначили професором раціональної механіки в Сорбонну. Науковий доробок Пуассона величезний. Він написав понад 300 праць. Пуассон ґрунтовно розробив багато розділів математичної фізики. У математиці істотне значення мають праці Пуассона, присвячені визначеним інтегралам, рівнянням в частинних похідних, теорії ймовірностей, варіаційному численню, рядам тощо.

При вивчення теми “Теореми додавання і множення ймовірностей” доцільно навести задачу видатного вітчизняного математика С.Н. Бернштейна.

Задача Бернштейна. Із урни навмання виймають одну із чотирьох ідентичних за формою куль. На одній із куль написано цифру 1, на другій – цифру 2, на третій – 3, на четвертій кулі – всі три цифри: 1, 2 і 3. Чи є попарно незалежними ці події?

Позначимо:

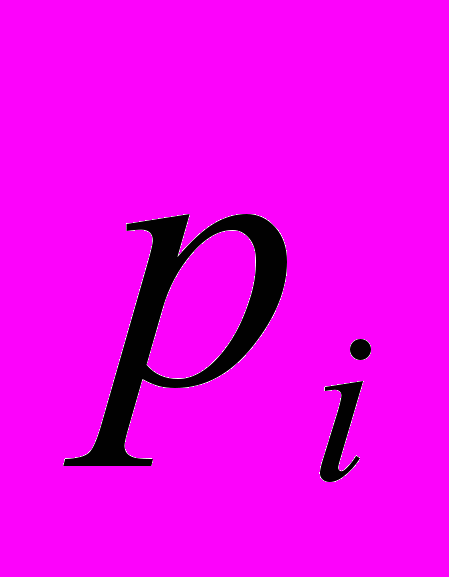– ймовірність того, що на вийнятій кулі знайдеться зображення цифри і;

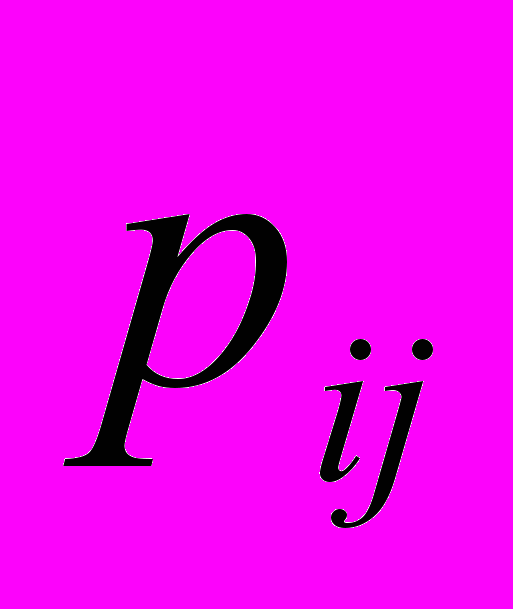– ймовірність того, що на вийнятій кулі знайдуться зображення цифр і і j;

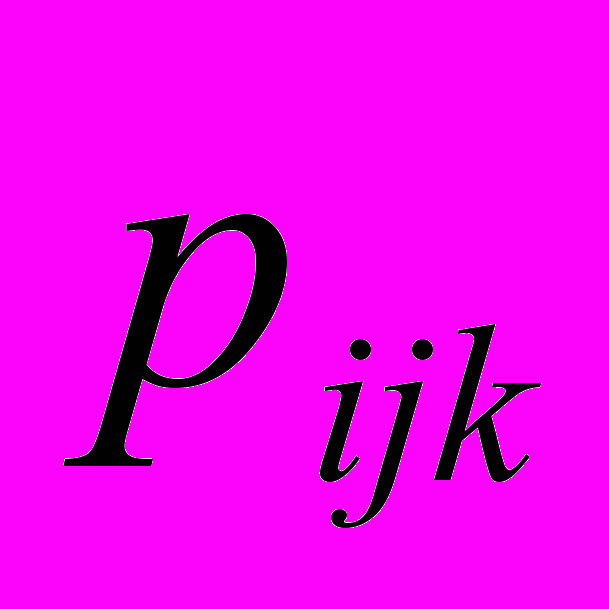– ймовірність того, що на вийнятій кулі знайдуться зображення цифр і, j і k.

Прямий підрахунок цих ймовірностей дає такий результат:

; , , ;

.

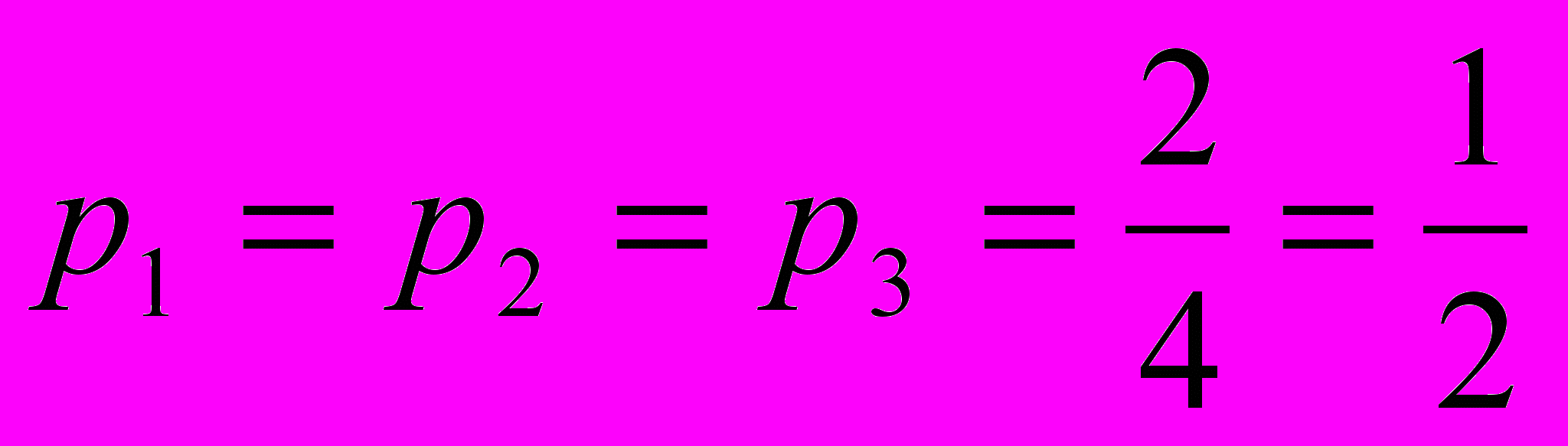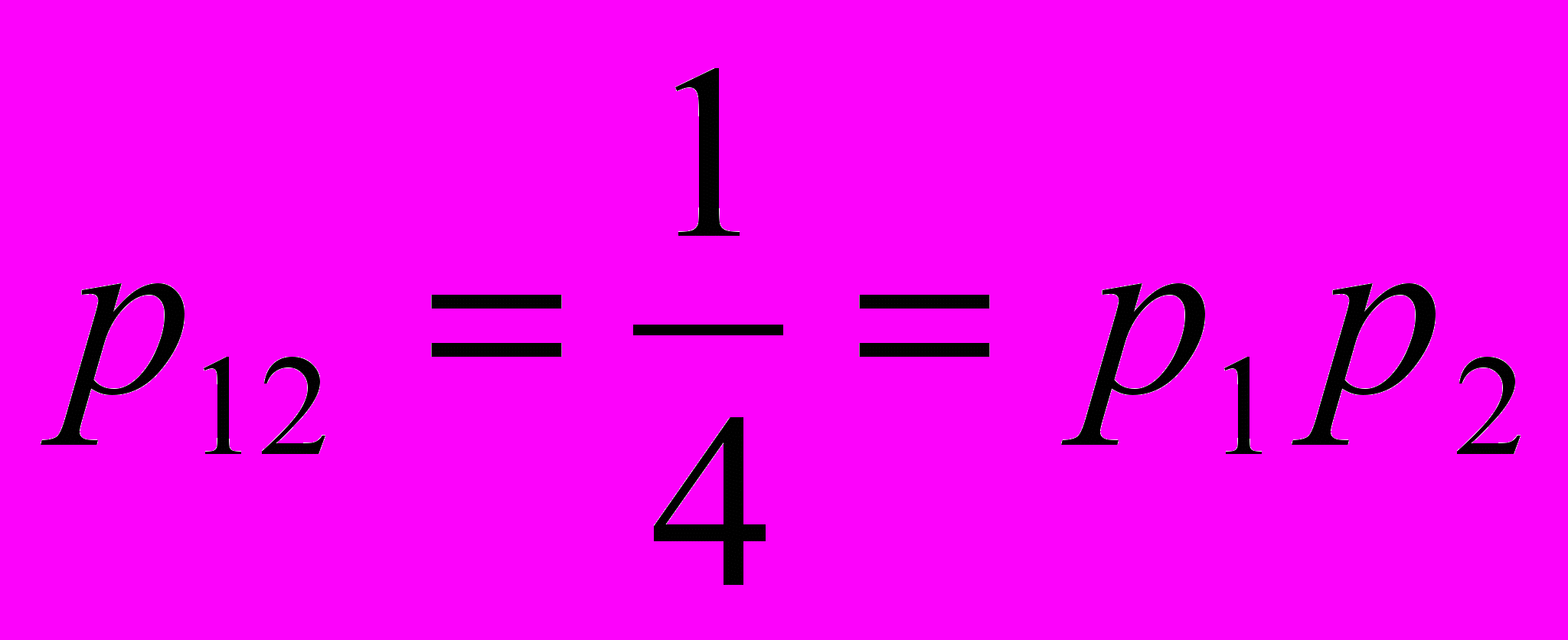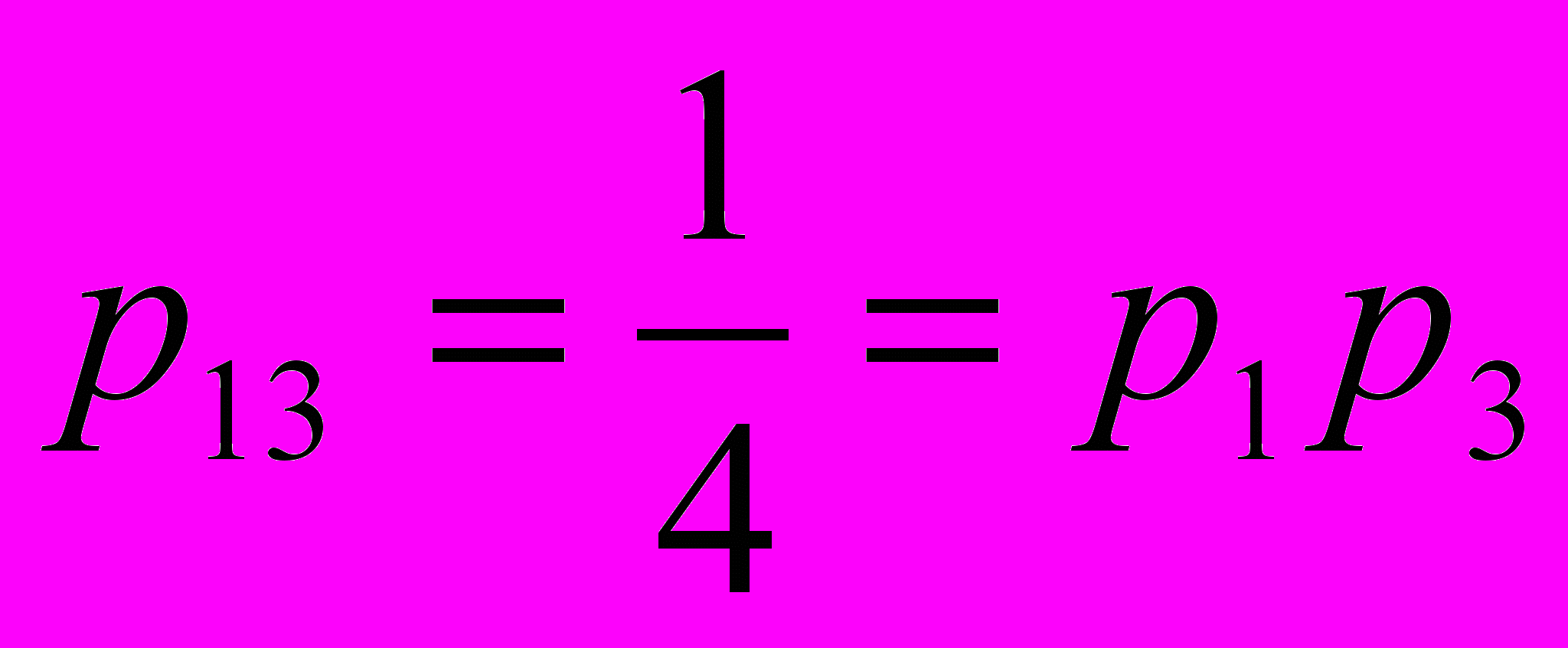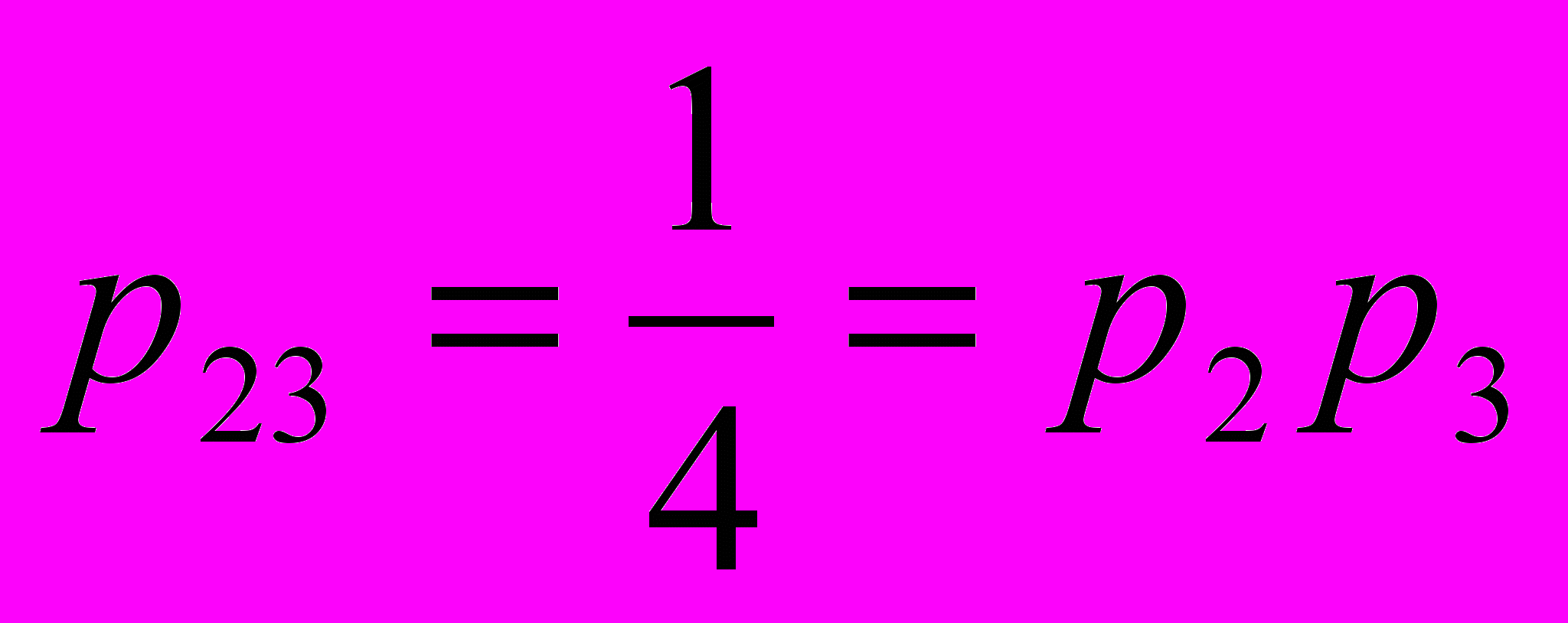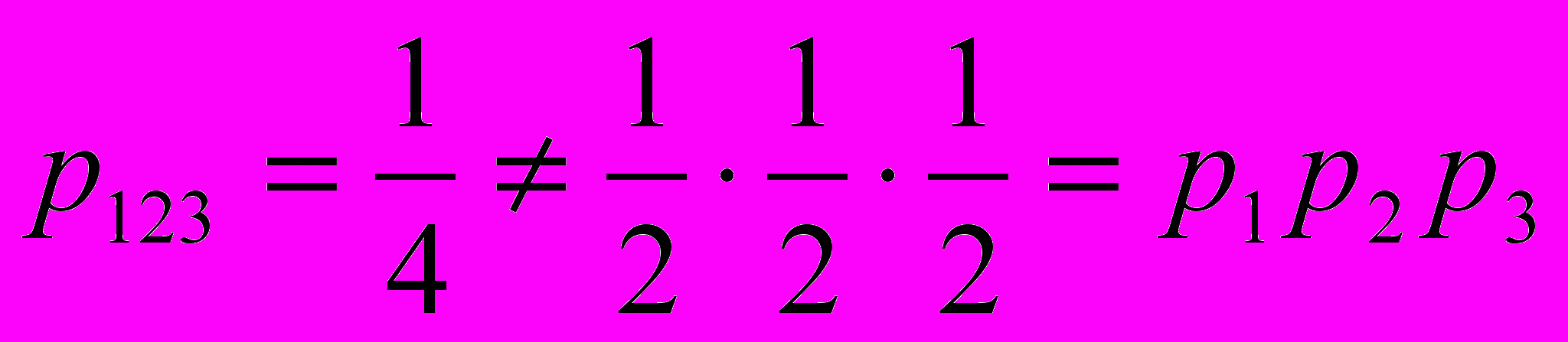Отже, введені події – поява окремих цифр – попарно незалежні. У той же час, всі три події не є незалежними в сукупності. Таким чином, незалежність в сукупності – більш сильна вимога, ніж попарна їх незалежність.

При вивченні теми “Формула повної ймовірності. Формула Байєса” слід сказати, що наслідком двох теорем ймовірностей – теореми додавання і теореми множення – є формули повної ймовірності і формула Байєса.

Т. Байєс (Томас Бейєс) (1702-1761) – англійський математик, священик, був членом Лондонського Королівського товариства. У сучасній теорії ймовірностей і математичній статистиці важливу роль відіграють формули Байєса, які дають можливість емпірично оцінювати ймовірність подій (гіпотез).

При вивченні теми “Геометрична ймовірність” можна розв’язати такі історичні задачі.

Задача про зустріч (1886 р.). Дві особи А і В домовились зустрітися в певному місці, причому вони приходить незалежно один від одного у випадковий момент між 12 і 13 годинами. Той, хто приходить першим, чекає 20 хв., і якщо другий за цей час не прийшов, перший уходить. Знайти ймовірність зустрічі А і В, якщо моменти їх приходу незалежні, і час приходу кожного протягом години непередбачуваний.

Розв’язування. Позначимо моменти приходу А і В відповідно через х і у. тоді за простір елементарних подій природно прийняти квадрат  у площині х0у:

.

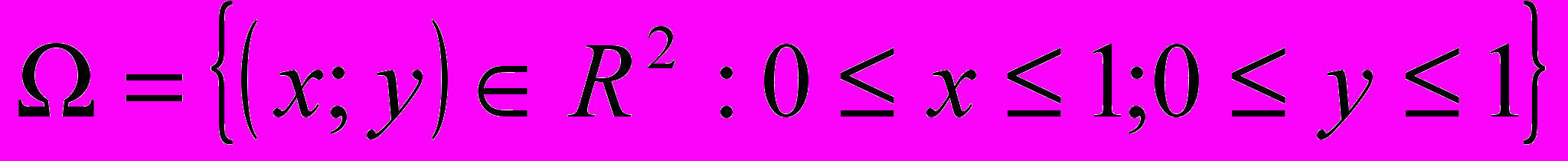Згідно з умовою, А і В зустрінуться тоді, коли 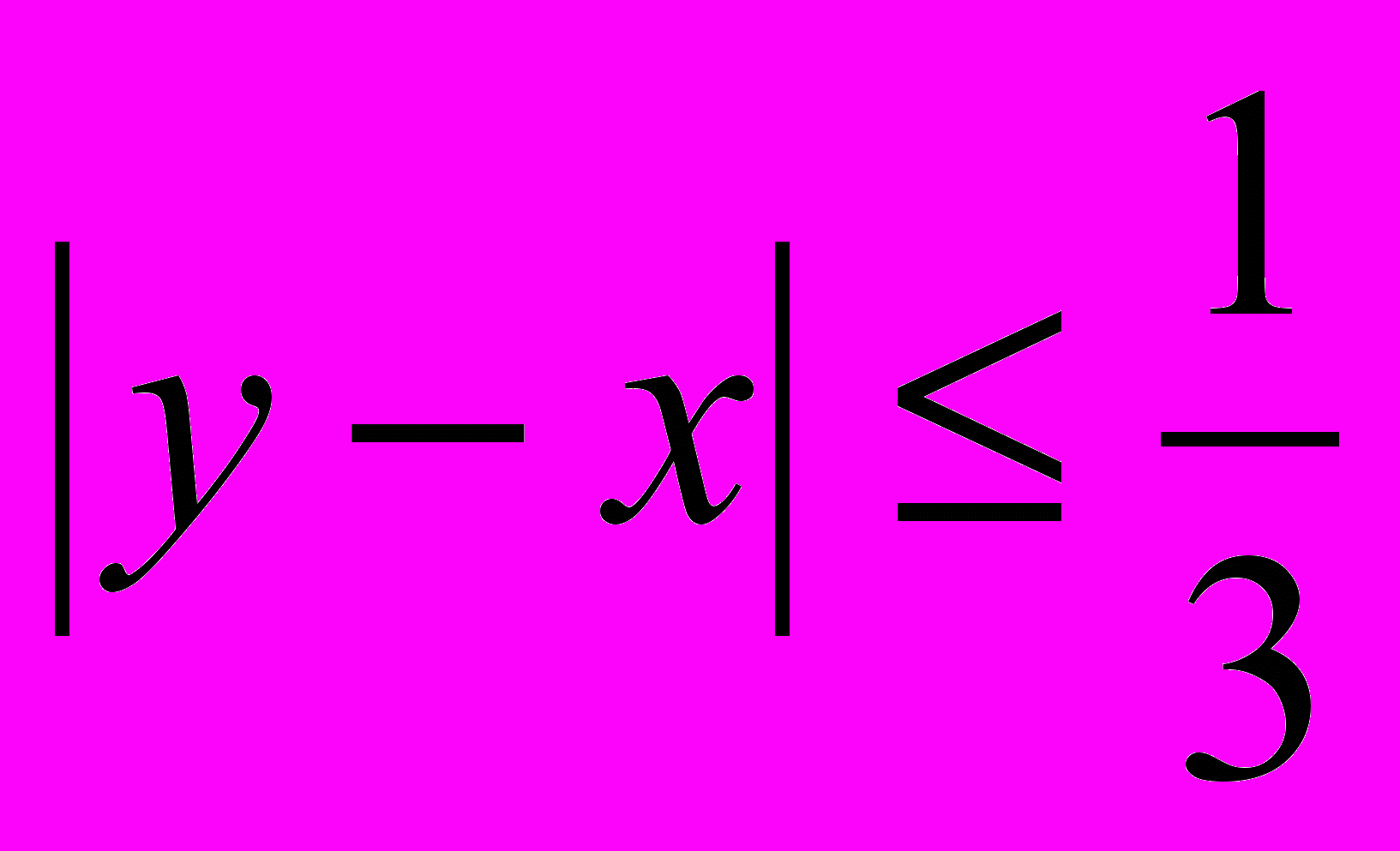(різниця між моментами приходу не перевищує 20 хвилин); це означає, що зустрічі (подія С) відповідають точки квадрату, для яких виконується зазначена нерівність: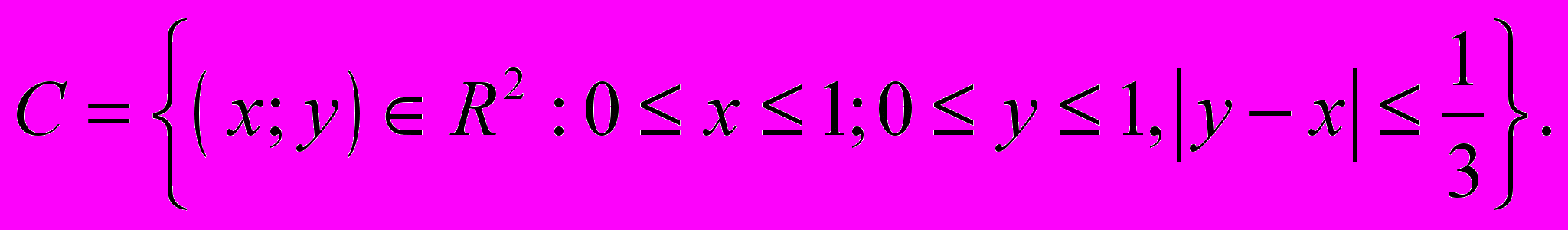



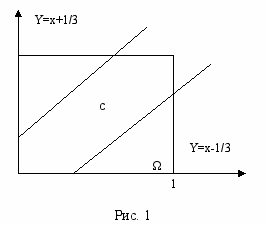
Нерівність 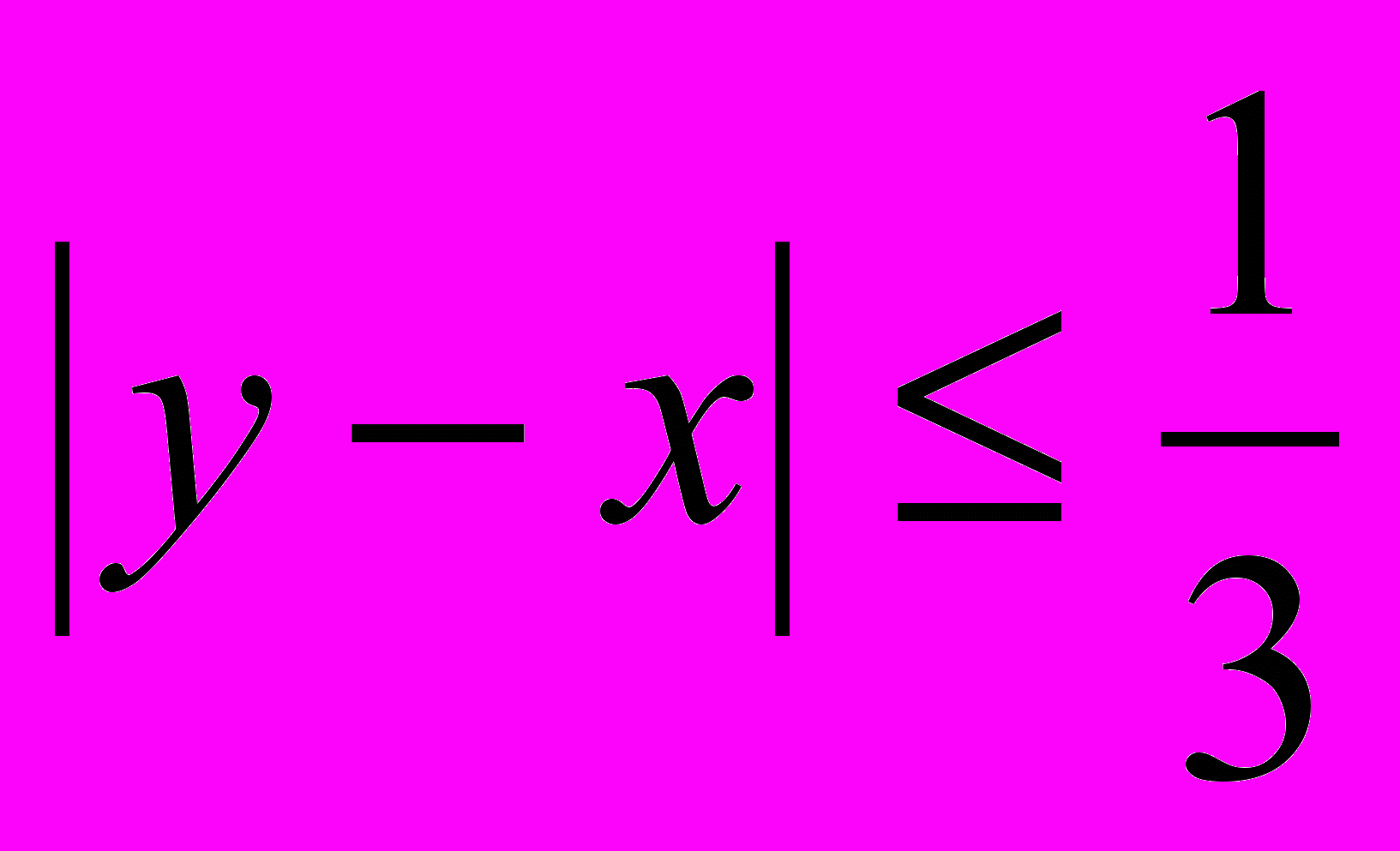, еквівалентна нерівності 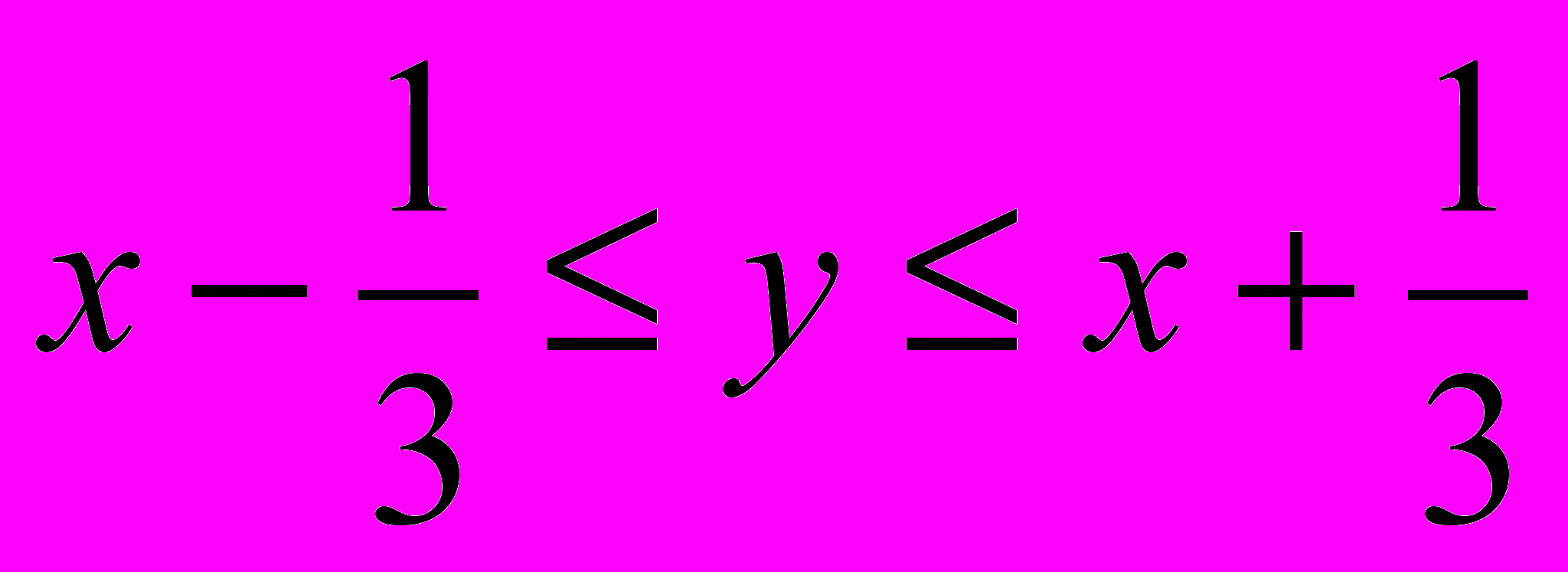(їй відповідає область, заштрихована на рис.1).

Отже, шукана ймовірність за формулою геометричної ймовірності дорівнює:

.

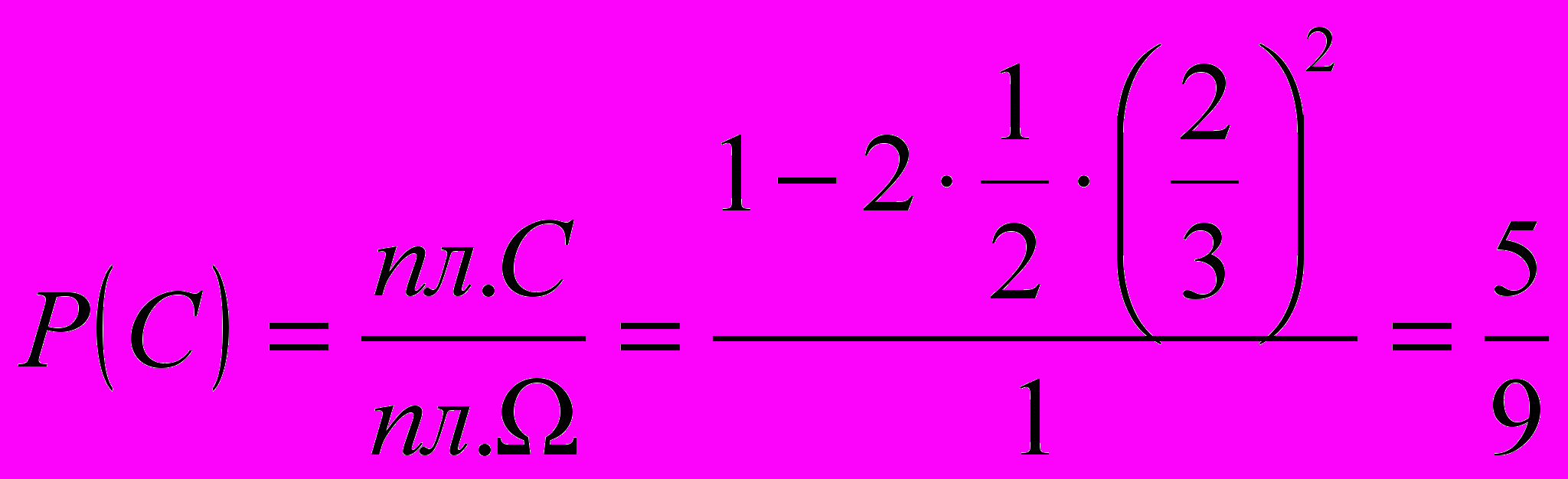Слід відмітити, що геометричне означення ймовірності не раз піддавалося критиці з боку багатьох математиків. Один з критиків його творчості був французький математик Жозеф Бертран (ХІХ ст.). Він розглянув низку задач, які, залежно від вибору методу їх розв’язування, приводять до різних результатів.

Отже, на сучасному етапі постає завдання подальшої науково-практичної розробки сучасних проблем гуманізації навчання та широкого впровадження відповідних психолого-педагогічних і методичних надбань у практику роботи вищих навчальних закладів різних рівнів акредитації. Тут доцільним є введення елементів історизму в викладання дисциплін фундаментального циклу, зокрема вищої математики.