Geum.ru

Учебно-методический комплекс учебной дисциплины «механика, основы механики сплошных сред» вузовского компонента цикла опд. Ф. 1 для специальностей 010400 физика и 013800 радиофизика и электроника составитель

Вид материалаУчебно-методический комплекс
E и момента импульса p
Контрольные вопросы Цикл 0
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11

Задача 4


Определить закон движения и уравнение траектории методом Якоби-Гамильтона в задаче о сферическом маятнике.

Запишем уравнение Гамильтона-Якоби для функции действие S(φ,θ,t), заменив импульсы в функции Гамильтона на соответствующие производные действия по координатам и приравняв функцию Гамильтона производной действия по времени со знаком минус

.

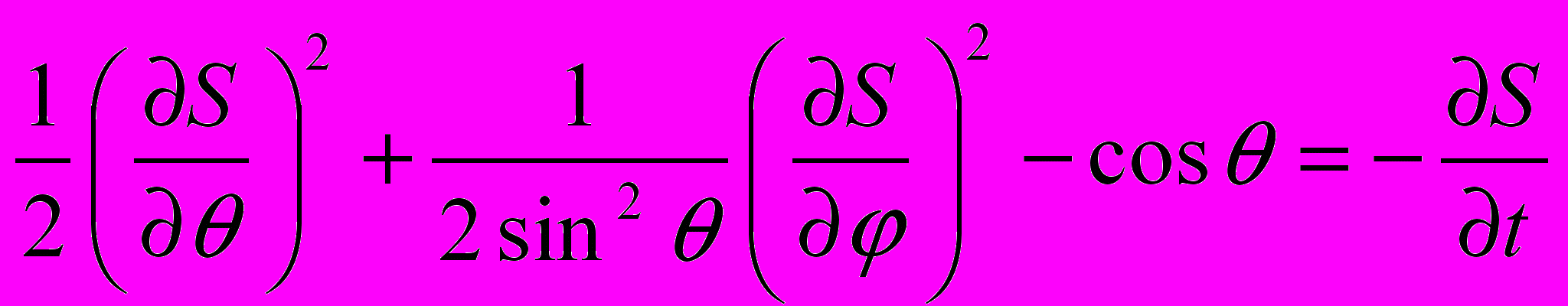Отделяя зависимость от времени S(t, φ, θ) = - Et + S0(φ, θ), получим уравнение для укороченного действия S0(φ, θ) в виде

.

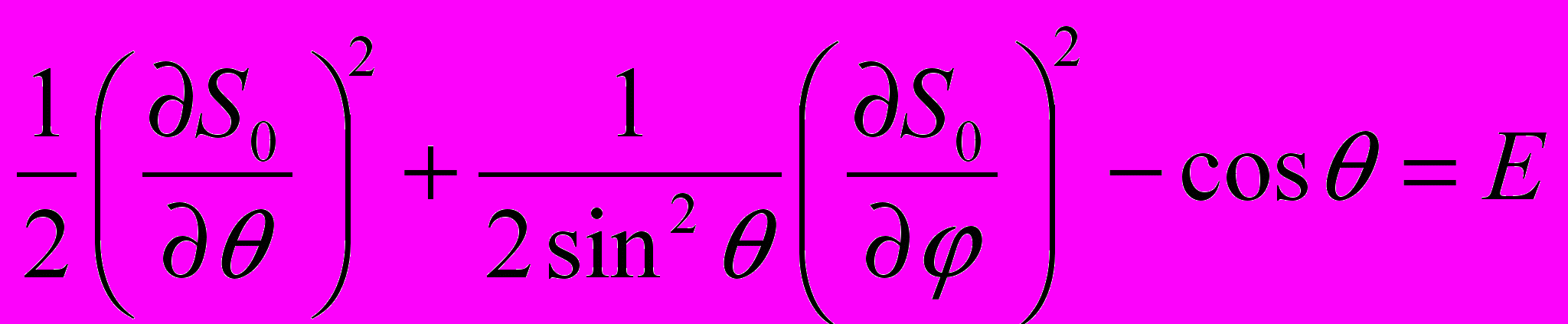В этом уравнении можно также отделить зависимости от углов, то есть представить искомое решение в виде

S0(φ, θ) = Sφ(φ) + Sθ( θ).

Такая возможность возникает в связи с отсутствием аргумента φ в уравнении.

После подстановки в уравнение записанной суммы, мы должны потребовать его тождественного выполнения

.

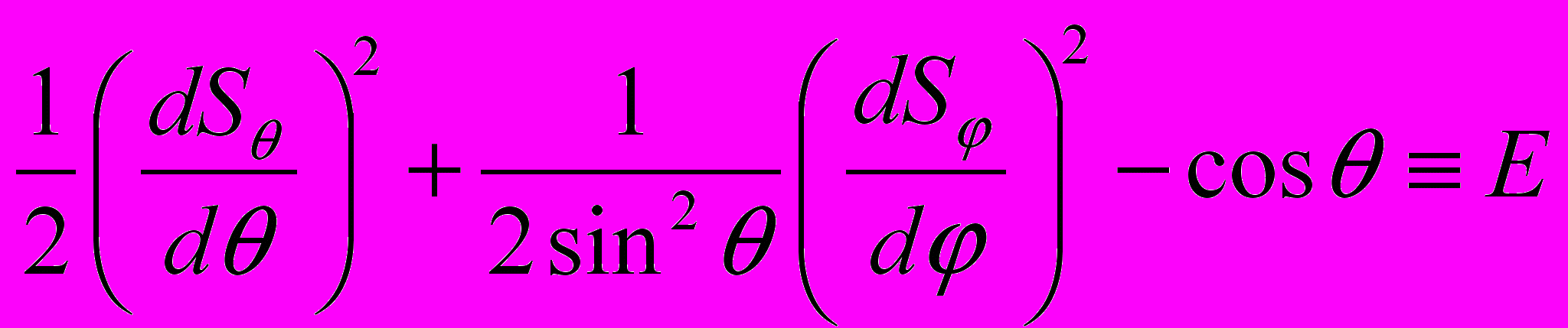Для того чтобы тождество выполнялось при любых значениях, в частности, угла φ, производная dSφ/dφ должна быть постоянной dSφ/dφ = pφ ≡ Mz = const.

Отсюда Sφ(φ) = pφφ.

Таким образом, полное действие имеет вид

S(t, φ, θ) = - Et + pφφ + Sθ(θ),

где последнее слагаемое находится из простого уравнения



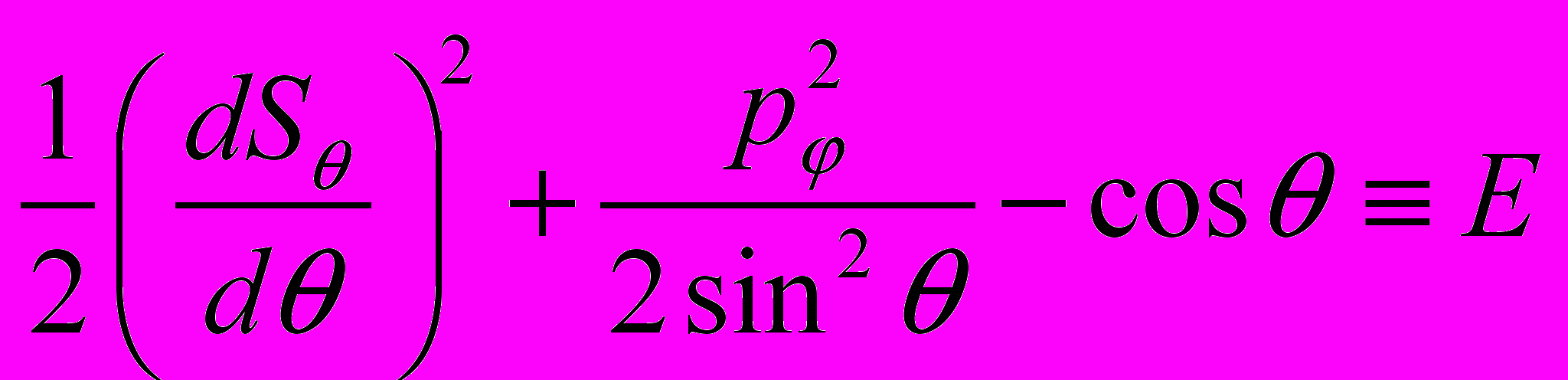
и имеет вид

.

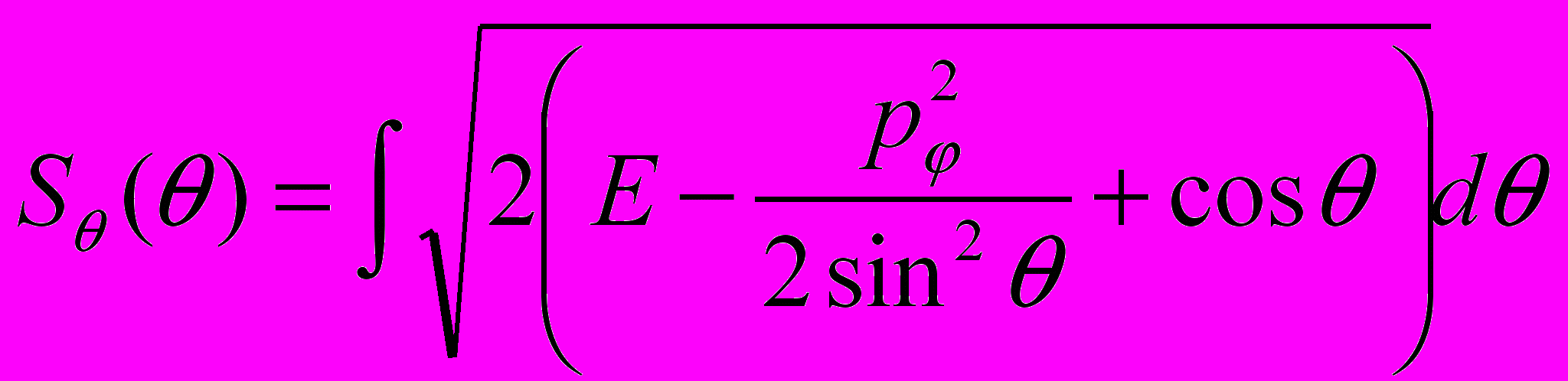Укороченное действие, таким образом, имеет вид



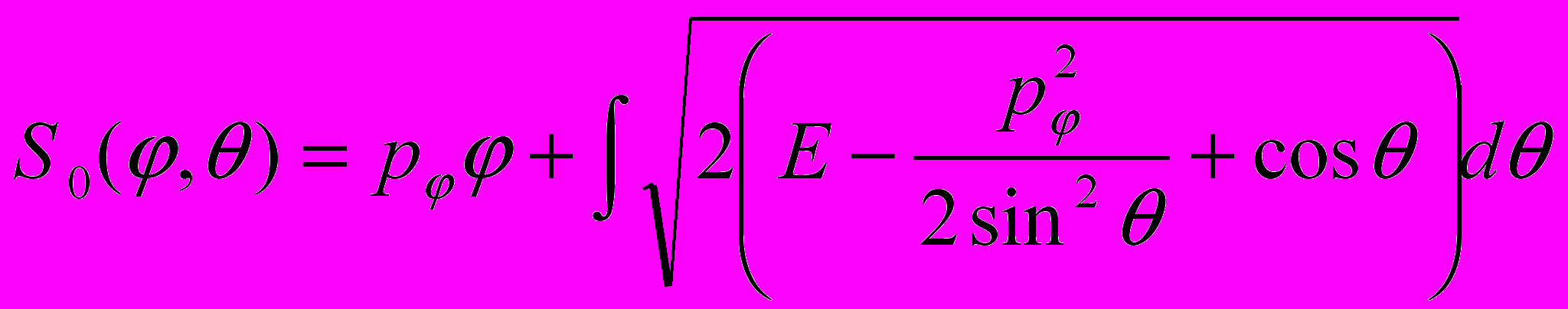
Итак, в нашей задаче полный интеграл уравнения Гамильтона-Якоби зависит от двух постоянных – полной энергии E и момента импульса pφ. Мы получим закон движения, дифференцируя полный интеграл по этим постоянным и приравнивая результат другим постоянным. А именно,

.

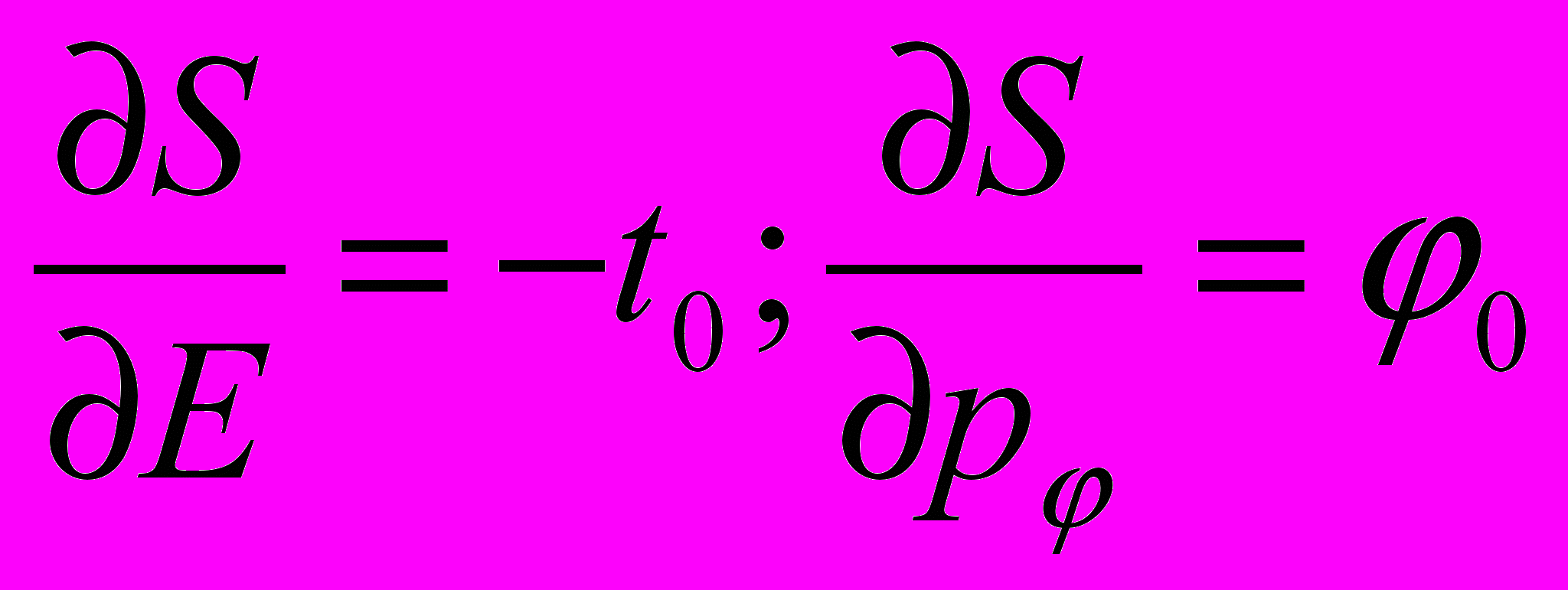Первое соотношение дает неявное выражение закона изменения координаты θ(t). Второе соотношение определяет уравнение траектории.


Контрольные вопросы

Цикл 0

Задачи

  1. Свободная частица на прямой линии.


  1. Частица на прямой линии в вязкой среде.


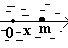
  1. Частица на прямой в поле тяжести.


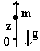
  1. Свободная частица на окружности.


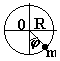
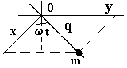
  1. Частица, скользящая по равномерно вращающемуся стержню.


  1. Частица на конце пружинки (одномерный осциллятор).


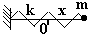
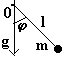
  1. Частица в поле тяжести на конце стержня (плоский математический маятник).


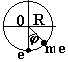
  1. Заряженная частица на окружности в поле закрепленного заряда.


  1. Частица на прямой линии в поле гармонической силы.



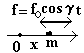
Вопросы

  1. Как описывается положение системы в задачах 1-9? В чем отличия и совпадение?
  2. Что такое одномерная система и число степеней свободы?
  3. Как записываются импульс (момент импульса) и энергия в задачах 1-9? Какие отличия в поведении этих функций в разных задачах, и чем эти отличия объясняются?
  4. Дайте определения диссипативной, консервативной и нестационарной системы.
  5. Что называется состоянием механической системы? Является ли импульс (момент импульса) независимой характеристикой состояния? То же в отношении энергии.
  6. Дайте определение и классификацию связей. Является ли пружинка из задачи 6 связью?
  7. Опишите связи в задачах 4,5,7,8.
  8. Что такое силы реакции? Как направлена сила реакции в случае идеальной связи?
  9. Обобщив опыт решения задач 4,5,7,8, опишите, как определяются силы реакции в случае идеальной связи.
  10. Какой физический смысл сил реакций в задачах 4,5,7,8?
  11. В каких формах можно записать уравнения движения одномерных систем?
  12. Запишите уравнения движения задач 1-9 в разных формах.
  13. Что означает ковариантность (иногда говорят «форм инвариантность») уравнений движения и в чем отличие ковариантности от инвариантности?
  14. Что называют преобразованиями систем отсчета?
  15. В чем состоит принцип, или постулат детерминизма? Покажите, что из него следует указанная форма уравнений движения.
  16. Что означает масштабная инвариантность, инвариантность относительно сдвигов и отражений в пространстве и времени?
  17. Какими свойствами инвариантности обладают уравнения движения в задачах 1 – 9?
  18. Объясните выбор масштабов в рассмотренных задачах и запишите их уравнения движения после масштабирования.
  19. Что называют системой отсчета? Поясните физический смысл сдвигов, преобразований масштабов и отражений в пространстве и времени.
  20. Поясните физический смысл коэффициентов, определяющих инвариантные однородные преобразования координат и времени свободной частицы.
  21. Что называется преобразованием Галилея?
  22. Что называют инерциальными системами отсчета?
  23. Как выглядят однородные пространственные преобразования, оставляющие инвариантными уравнения движения свободной частицы на плоскости?
  24. Что такое ортонормированная система координат и ортогональные преобразования на плоскости?
  25. В чем состоит классическое правило сложения скоростей?
  26. Поясните смысл абсолютности времени и относительности пространства в классической модели.
  27. Сформулируйте релятивистский принцип относительности.
  28. Что такое интервал в пространстве-времени? Поясните его физический смысл.
  29. Напишите преобразования Лоренца и поясните их физический и математический смысл.
  30. Каков смысл изменений интервалов длины и времени, следующих из преобразований Лоренца? Что называется γ-фактором?
  31. Как изменяется уравнение движения свободной частицы при нелинейном преобразовании координаты? В чем физический смысл этого преобразования?
  32. Что называется неинерциальной системой отсчета, и как изменяется уравнение движения свободной частицы при переходе в равномерно ускоренную систему отсчета?
  33. Каков физический смысл сил инерции?
  34. Что такое закон движения механической системы и как он определяется в большинстве задач?
  35. Получите законы движения рассмотренных задач аналитически.
  36. Чем отличается процесс решения линейных дифференциальных уравнений от нелинейных?
  37. Каков смысл констант, входящих в закон движения? Поясните смысл различных наборов постоянных в рассмотренных задачах.
  38. Дайте полный анализ физического, качественного характера движения рассмотренных систем при различных начальных условиях?
  39. С какими типами движений Вы познакомились?
  40. В чем состоит процесс линеаризации нелинейных уравнений движения, в каком случае, и с какой целью он проводится?
  41. Как инвариантные свойства уравнений движения связаны с постоянными в законе движения?
  42. Как, используя инвариантность, можно упростить запись закона движения? Дайте анализ всех рассмотренных задач.
  43. Что такое фазовое пространство и фазовые траектории?
  44. Каким важным свойством и почему обладают фазовые траектории?
  45. Какова структура фазового и расширенного фазового пространства в рассмотренных задачах?
  46. Что такое канонические переменные, в каких задачах они вводятся и зачем?
  47. Что представляет собой функция Лагранжа, и какие механические системы не являются лагранжевыми?
  48. Каков «алгоритм» определения функции Лагранжа системы со связями?
  49. Как определяется обобщенный импульс и как связаны законы сохранения обобщенного импульса и энергии со свойствами функции Лагранжа?
  50. Какие преобразования функции Лагранжа не меняют уравнений движения системы?
  51. Сформулируйте принцип наименьшего действия Гамильтона. Что из него следует?
  52. Как определяется функция Гамильтона механической системы, и для каких систем она существует?
  53. Что представляют собой канонические уравнения?
  54. Как связаны свойства функции Гамильтона с законами сохранения импульса и энергии?
  55. В чем особенность фазовых координат «действие-угол»?
  56. Что такое канонические преобразования фазовых координат, и каким условиям они должны удовлетворять?
  57. Что представляет собой уравнение Гамильтона-Якоби?
  58. Что такое полный интеграл уравнения Гамильтона-Якоби, и как, найдя этот интеграл, можно найти закон движения системы?
  59. Найдите закон движения в задачах 1, 3 - 8, используя метод Якоби-Гамильтона.
  60. Что такое производящая функция канонического преобразования?
  61. Как выглядят производящие функции движения, тождественного преобразования, точечного преобразования и перехода к переменным «действие-угол»?