Geum.ru

Учебно-методический комплекс учебной дисциплины «механика, основы механики сплошных сред» вузовского компонента цикла опд. Ф. 1 для специальностей 010400 физика и 013800 радиофизика и электроника составитель

Вид материалаУчебно-методический комплекс
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11

Цикл 1

Задачи

  1. Гармонический осциллятор в среде с линейной вязкостью («Механика», §25).


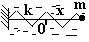
  1. Заряженная частица m, e на равномерно вращающемся вокруг вертикальной оси стержне в поле двух таких же по величине и знаку зарядов, закрепленных на стержне симметрично относительно оси вращения на расстоянии a/2 от нее.


  1. Заряженная частица m, e на вертикальной окружности радиуса R в поле закрепленного в нижней точке окружности того же по величине и знаку заряда и в поле тяжести g.


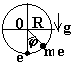
  1. Частица m на вертикальной окружности радиуса R, равномерно вращающейся с угловой частотой ω вокруг вертикальной оси, проходящей через ее центр, в поле тяжести g.



  1. Гармонический осциллятор в поле вынуждающей гармонической силы («Механика», §22).


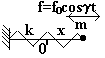
  1. Гармонический осциллятор в поле вынуждающей гармонической силы и в среде с линейной вязкостью («Механика», §26).


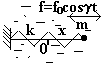
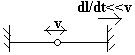
  1. Частица m в бесконечно глубокой потенциальной яме с медленно движущейся стенкой (адиабатический процесс, «Механика», §49).


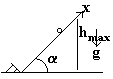
  1. Частица на наклонной плоскости с медленно меняющимся углом наклона. Найти зависимость высоты подъема от угла наклона, используя адиабатический инвариант.


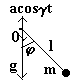
  1. Плоский математический маятник с вертикально колеблющейся точкой подвеса («Механика», гл.1, зад.3 в), §30, зад. 1 к §30).


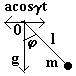
  1. Плоский математический маятник с горизонтально колеблющейся точкой подвеса («Механика», гл.1, зад.3 б), §30, зад. 2 к §30).



Вопросы

  1. Как выглядит уравнение движения гармонического осциллятора в среде?
  2. Как использование масштабной инвариантности позволяет записать уравнение движения, и как выглядит общее решение (закон движения)?
  3. Что представляет собой закон движения осциллятора в среде при сильном затухании, и как выглядят фазовые траектории в этом случае?
  4. Каков закон движения гармонического осциллятора в среде при слабом затухании, каковы фазовые траектории?
  5. Что такое логарифмический декремент затухания, и по какому закону в среднем рассеивается энергия гармонического осциллятора в среде?
  6. Запишите функцию Лагранжа задачи 11 в общем и безразмерном виде. Поясните роль и физический смысл безразмерного параметра.
  7. Запишите уравнение движения задачи 11, следующее из уравнения Лагранжа.
  8. Проведите полный анализ потенциальной энергии в задаче 11. Поясните характер движения при различных значениях безразмерного параметра и различных начальных условиях. Какой физический смысл имеет критическое значение безразмерного параметра?
  9. Как выглядят фазовые портреты задачи 11 при k < kcr и k > kcr?
  10. Как определяется период нелинейных колебаний?
  11. Определите частоты гармонических колебаний задачи 11 вблизи устойчивых положений равновесия при различных значениях безразмерного параметра.
  12. Запишите функцию Гамильтона и уравнения движения в форме канонических уравнений задачи 11.
  13. Запишите и решите уравнение Гамильтона-Якоби задачи 11, получив полный интеграл и закон движения. Как выглядит закон движения в канонических переменных?
  14. Запишите функцию Лагранжа задачи 12 в общем и безразмерном виде. Поясните роль и физический смысл безразмерного параметра.
  15. Запишите уравнение движения задачи 12, следующее из уравнения Лагранжа.
  16. Проведите полный анализ потенциальной энергии в задаче 12. Поясните характер движения при различных значениях безразмерного параметра и различных начальных условиях.
  17. Как выглядят фазовые портреты задачи 12 при g < gcr и g > gcr?
  18. Как определяется период нелинейных колебаний?
  19. Определите частоты гармонических колебаний задачи 12 вблизи устойчивых положений равновесия при различных значениях безразмерного параметра.
  20. Запишите функцию Гамильтона и уравнения движения в форме канонических уравнений задачи 12.
  21. Запишите и решите уравнение Гамильтона-Якоби задачи 12, получив полный интеграл и закон движения. Как выглядит закон движения в канонических переменных?
  22. Запишите функцию Лагранжа задачи 13 в общем и безразмерном виде. Поясните роль и физический смысл безразмерного параметра.
  23. Запишите уравнение движения задачи 13, следующее из уравнения Лагранжа.
  24. Проведите полный анализ потенциальной энергии в задаче 13. Поясните характер движения при различных значениях безразмерного параметра и различных начальных условиях.
  25. Как выглядят фазовые портреты задачи 13 при ω < ωcr и ω > ωcr?
  26. Как определяется период нелинейных колебаний?
  27. Определите частоты гармонических колебаний задачи 13 вблизи устойчивых положений равновесия при различных значениях безразмерного параметра.
  28. Запишите функцию Гамильтона и уравнения движения в форме канонических уравнений задачи 13.
  29. Запишите и решите уравнение Гамильтона-Якоби задачи 13, получив полный интеграл и закон движения. Как выглядит закон движения в канонических переменных?
  30. Запишите функцию Лагранжа задачи 14 в общем и безразмерном виде. Поясните роль и физический смысл безразмерного параметра.
  31. Запишите уравнение движения задачи 14, следующее из уравнения Лагранжа.
  32. Что называется резонансом, и какой характер носит движение задачи 14 вблизи резонанса?
  33. Поясните смысл перехода в колеблющуюся систему отсчета в задаче 14.
  34. Запишите функцию Гамильтона и канонические уравнения задачи 14.
  35. Запишите уравнения движения задачи 15, в общем, и безразмерном виде. Поясните роль и физический смысл безразмерных параметров.
  36. Поясните смысл перехода к комплексному виду уравнения движения.
  37. Запишите закон движения задачи 15 в общем виде и поясните физический смысл этого решения. Почему можно ограничиться частным решением неоднородного уравнения, и зависит ли это решение от начальных условий движения?
  38. Исследуйте зависимость амплитуды и сдвига фазы от безразмерных параметров. Как ведет себя сдвиг фазы при слабом затухании вблизи резонанса?
  39. Исследуйте скорость «перекачки» энергии в зависимости от безразмерных параметров. Что такое дисперсионная кривая?
  40. На какие поверхности расслаивается расширенное фазовое пространство осциллятора в среде при наличии вынуждающей силы?
  41. К какому выводу приводит анализ движения частицы в одномерной яме с медленно меняющейся шириной?
  42. Что такое адиабатический инвариант в общем случае? Является ли адиабатический инвариант интегралом движения?