Учебно-методический комплекс учебной дисциплины «механика, основы механики сплошных сред» вузовского компонента цикла опд. Ф. 1 для специальностей 010400 физика и 013800 радиофизика и электроника составитель

Вид материала

Учебно-методический комплекс

Содержание Примеры решения задач Задача 1

Подобный материал:

• Рабочая программа «Механика и основы механики сплошных сред» Специальность 010400 физика,, 141.09kb.
• Учебно-методический комплекс учебной дисциплины «Литературы народов снг» (часть, 370.67kb.
• Учебно-методический комплекс учебной дисциплины «Литературы народов снг» (часть II), 280.88kb.
• Учебная программа дисциплины «Физическая механика сплошных сред» Бакалавриат 010600, 102.22kb.
• Учебно-методический комплекс учебной дисциплины Литература средних веков и Возрождения, 281.88kb.
• Учебно-методический комплекс учебной дисциплины Литература средних веков и Возрождения, 282.94kb.
• Учебно методический комплекс учебной дисциплины «религиоведение» вузовского компонента, 339.44kb.
• Теоретическая физика. Механика, 16.15kb.
• Учебно-методический комплекс учебной дисциплины «Математические методы моделирования, 335.12kb.
• Рабочая программа Наименование дисциплины «Механика» По специальности 261203. 65 Тпп, 260.39kb.

Примеры решения задач

Задача 1

Частица может двигаться по стержню, вращающемуся вокруг оси ему перпендикулярной с постоянной угловой скоростью ω.



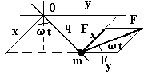
Определить силу реакции, действующую на частицу со стороны стержня.

Голономная, идеальная, но нестационарная в данном случае связь определяется соотношением y = xtg(ωt) между декартовыми координатами частицы на вращающемся стержне и временем. Сила реакции F направлена перпендикулярно стержню. Введем координату q вдоль стержня и выразим декартовые координаты x, y и проекции силы реакции F_x, F_y через q, F.

x = qcos(ωt); y = qsin(ωt);

F_x = -Fsin(ωt); F_y = Fcos(ωt)

Запишем 2-ой закон Ньютона в декартовых координатах



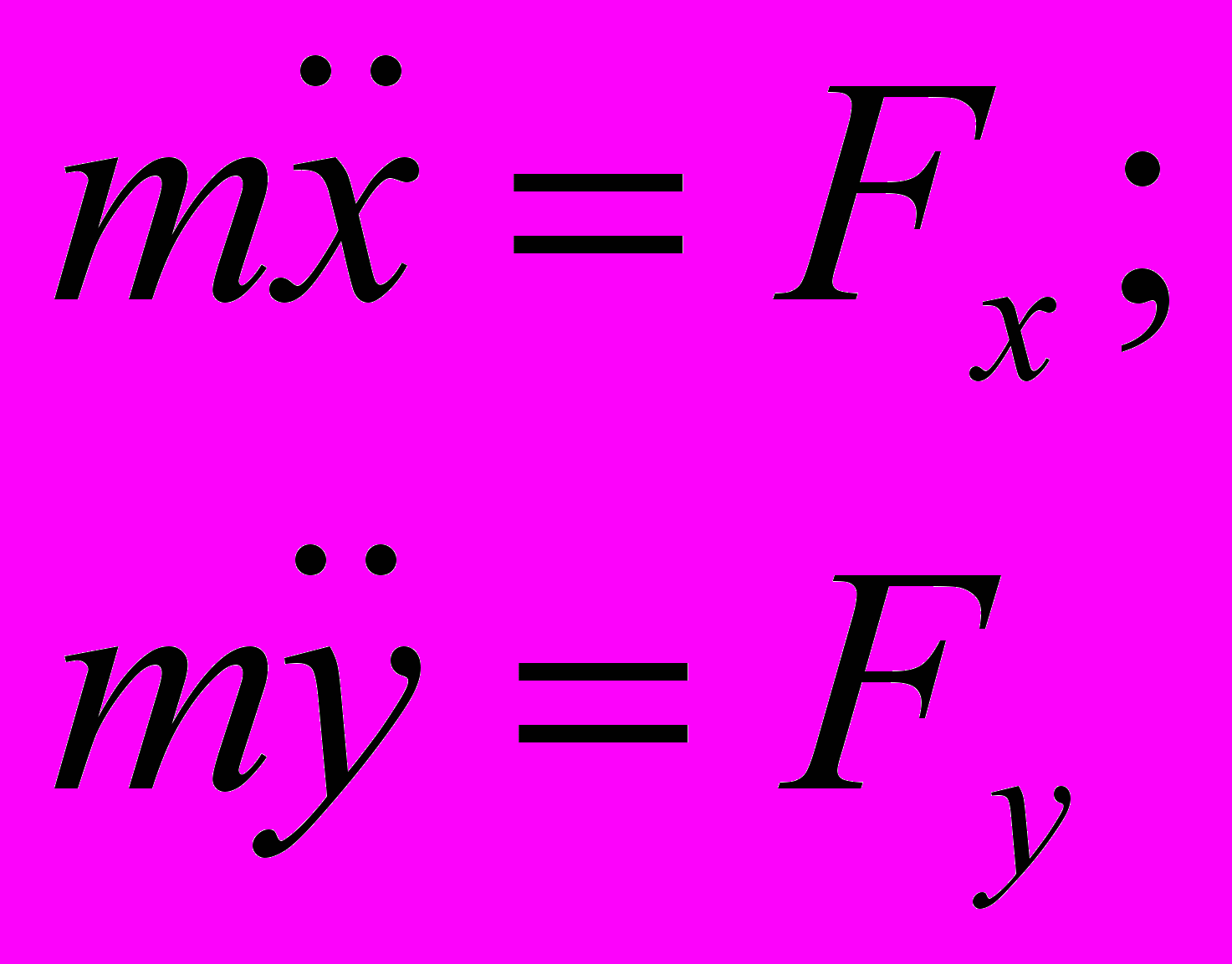
и подставим в него соответствующие производные 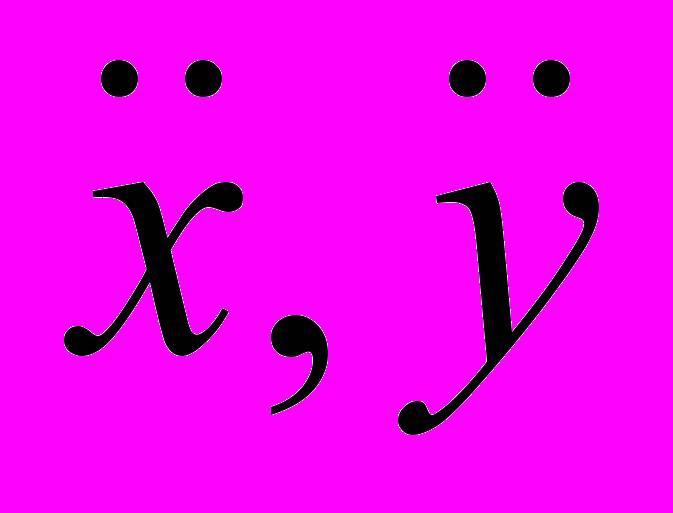и компоненты силы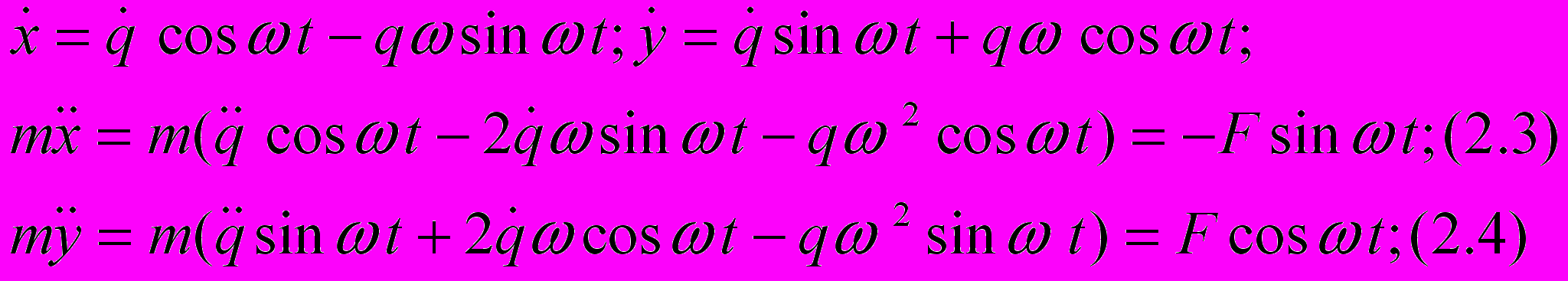



Теперь умножим уравнение (2.3) на –sin(ωt), а уравнение (2.4) на cos(ωt) и почленно сложим эти два уравнения. В результате получим силу реакции 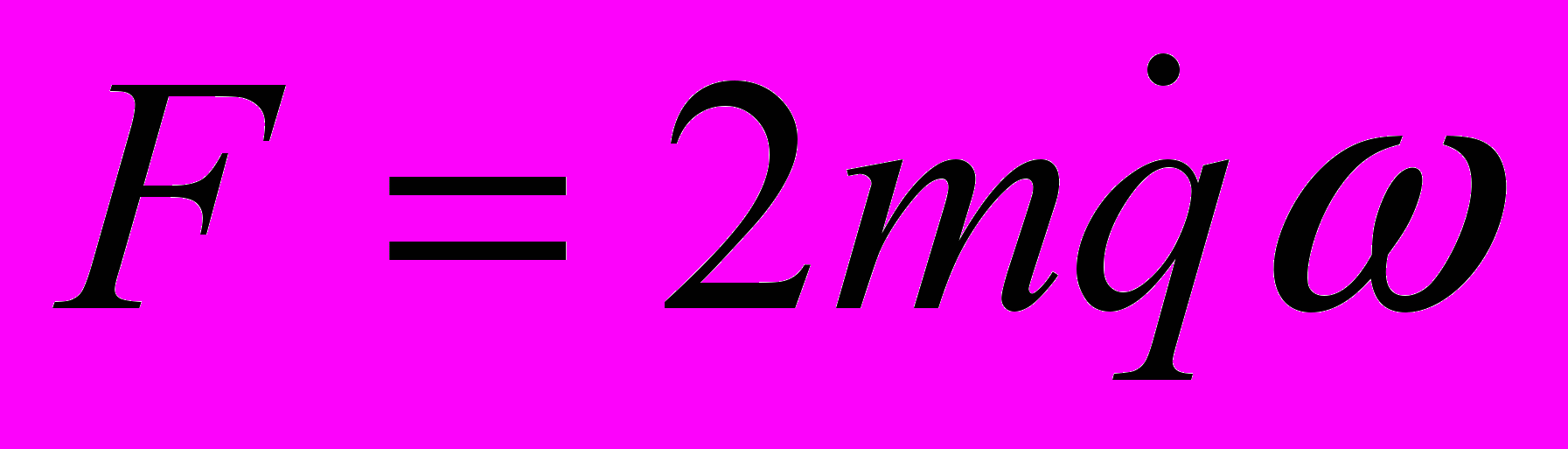. Смысл этого результата прост. Сила реакции стержня в точности компенсирует силу Кориолиса, действующую на движущуюся по вращающемуся стержню частицу. Направление силы реакции определяется знаком скорости 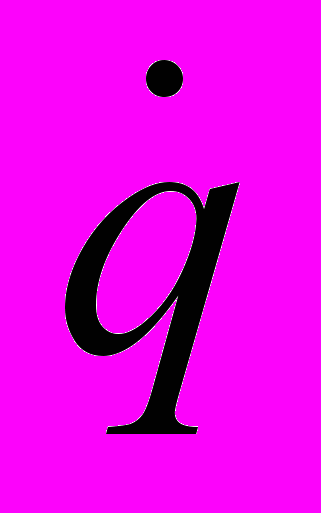, но всегда лежит вдоль прямой, перпендикулярной стержню.

Задача 2

Найти функцию Лагранжа и записать уравнения движения в задаче:

Точка подвеса плоского математического маятника колеблется вертикально с постоянной частотой γ и амплитудой a



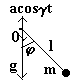
Найдем функцию Лагранжа такого маятника.

1. Выберем декартовую систему координат как в «Механике», с горизонтальной осью x, направленной слева направо и вертикальной осью y, направленной вниз. В этой системе координат функция Лагранжа частицы в плоскости в поле тяжести равна
   

.

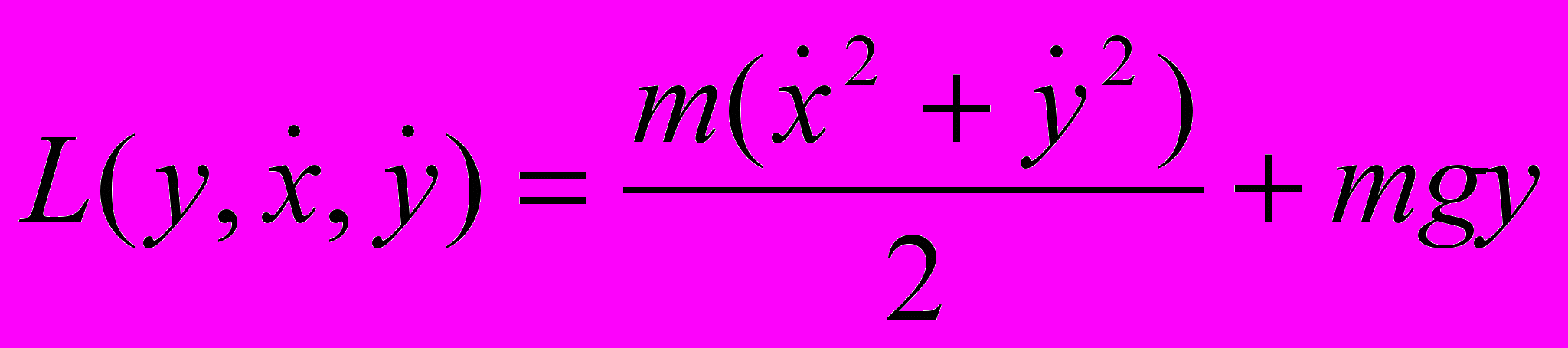2. Осуществим переход к независимой координате, углу отклонения от вертикальной оси φ, с учетом вертикального колебания точки подвеса маятника x = lsinφ; y = lcosφ + acos(γt).
   

В результате получим

.

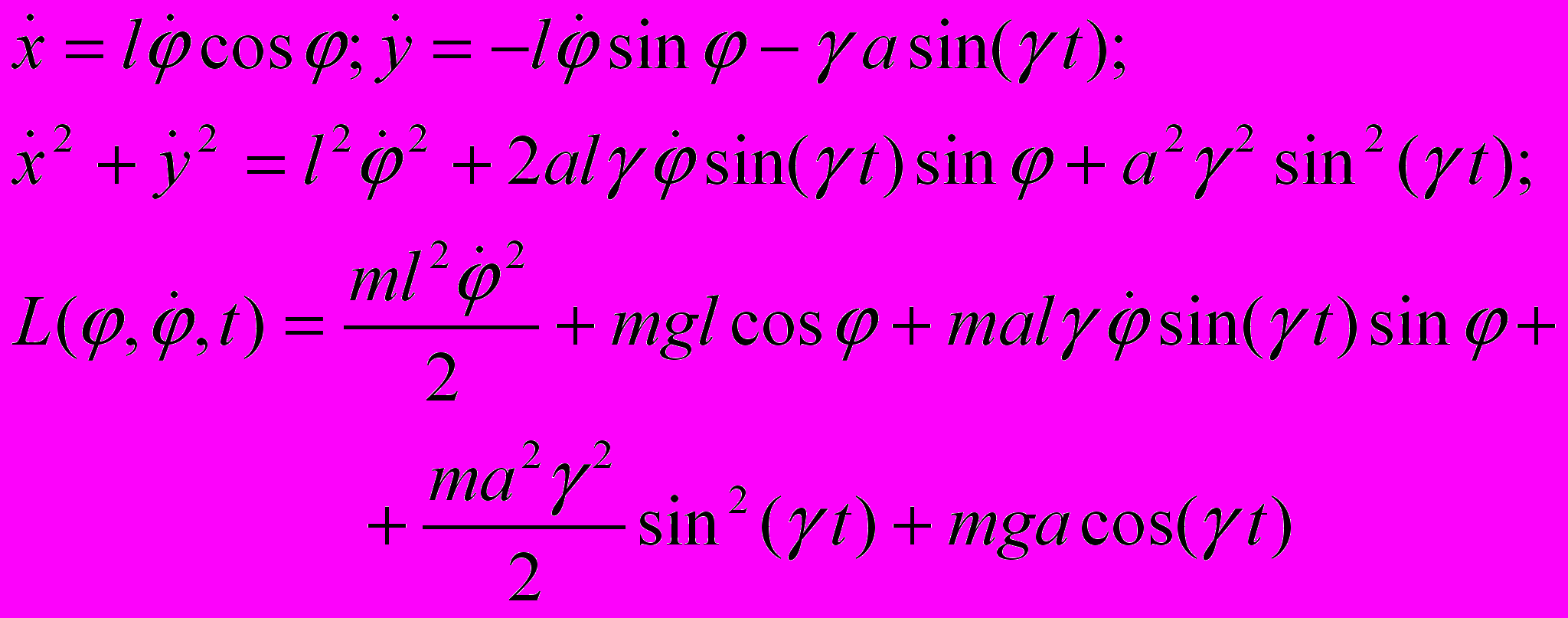Добавка к функции Лагранжа любой функции времени, а в общем случае, любой функции, сводящейся к полной производной по времени от некоторой функции координат и времени, не приводит к изменению уравнений Лагранжа (см. в связи с этим нулевой цикл, задачу 9 и §2 «Механики»). Поэтому, в частности, можно отбросить два последних слагаемых в выписанной функции Лагранжа, так как они зависят только от времени. Кроме того, можно преобразовать третье слагаемое, содержащее линейную зависимость от скорости, выделив в нем полную производную по времени

.

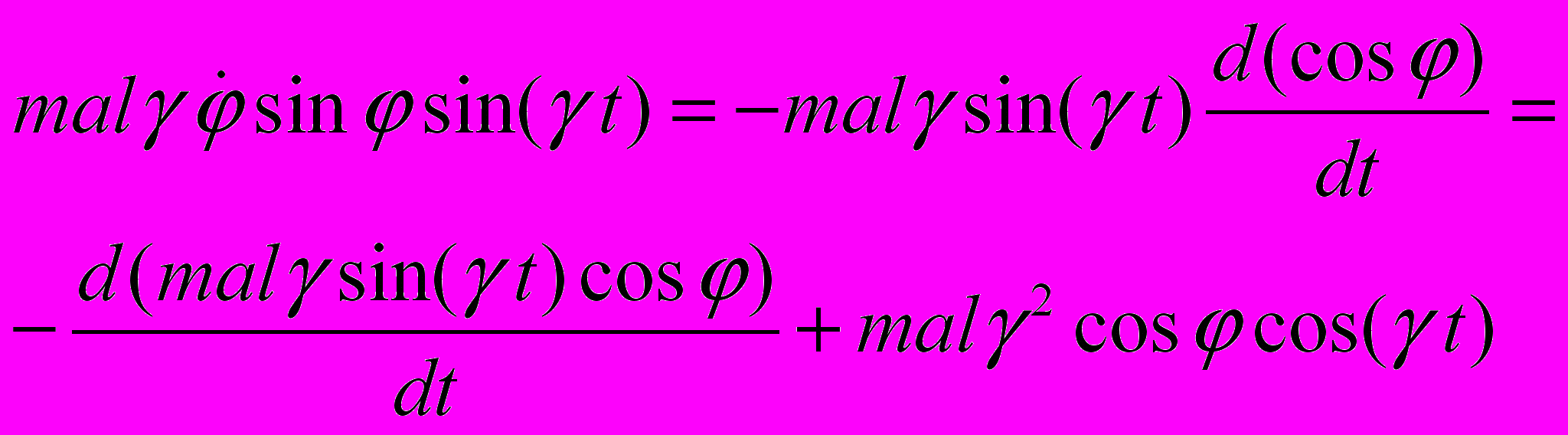Отбросив полную производную, мы избавляемся от линейной зависимости от скорости, и функция Лагранжа приобретает вид

.

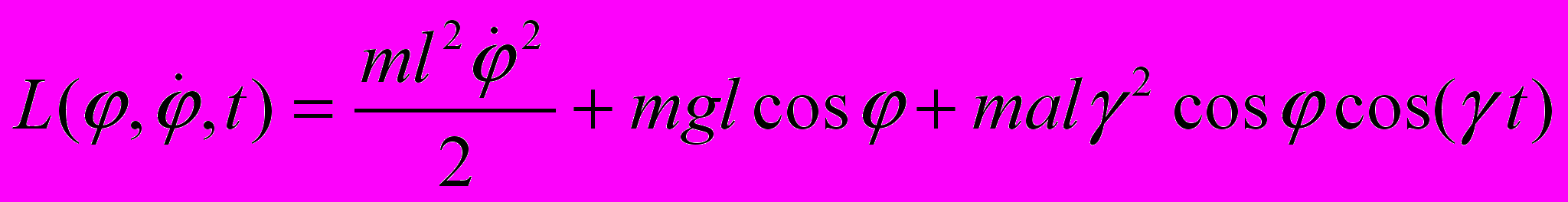3. Выбрав, как и в случае обычного плоского маятника, масштаб массы, длины и времени
   

,

получим безразмерную функцию Лагранжа.

Подставим полученную функцию Лагранжа в уравнение Лагранжа и запишем уравнение движения маятника с вертикально колеблющейся точкой подвеса

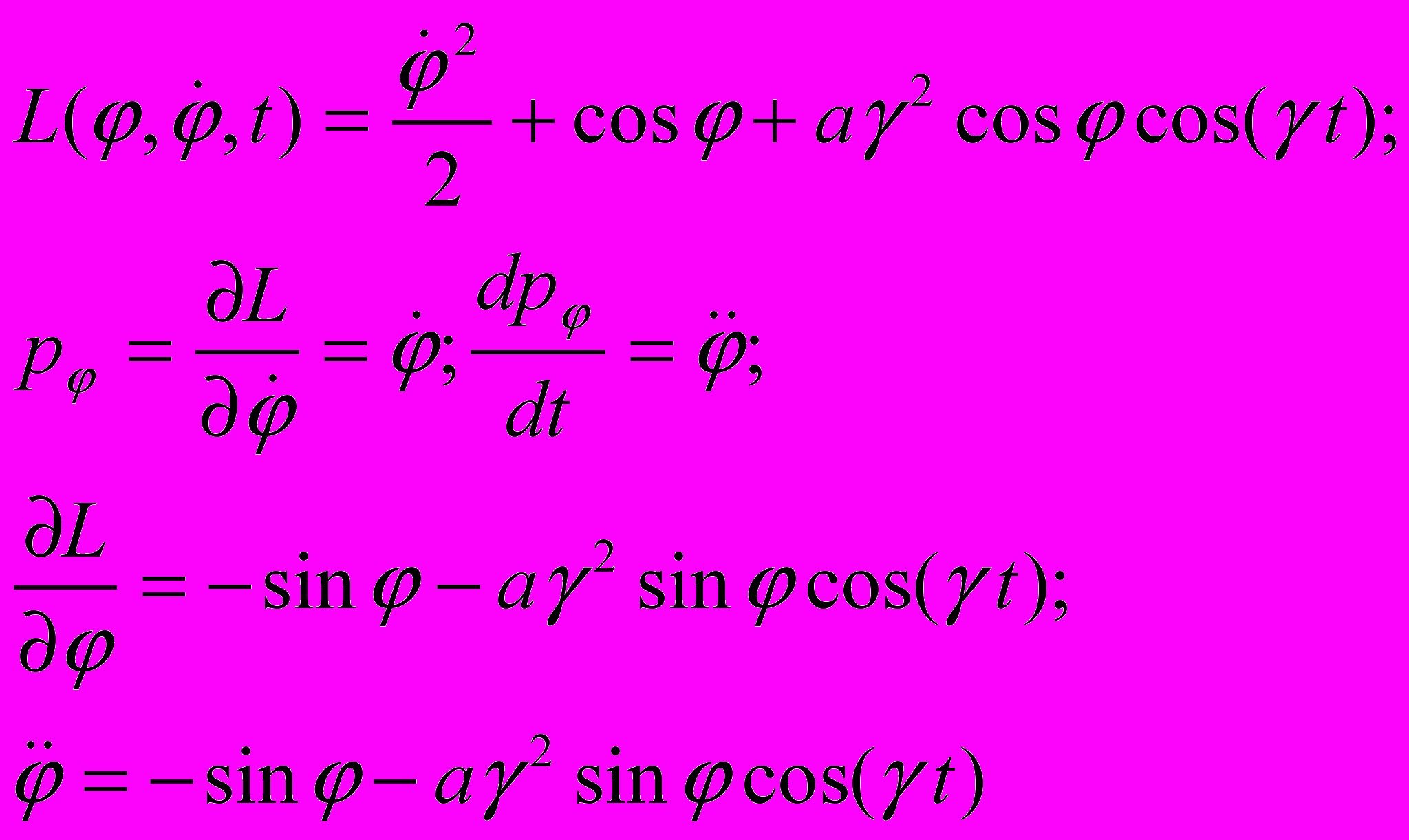
Задача 3

Частица движется по наклонной плоскости в поле тяжести, отражаясь упруго от установленного внизу отбойника. Угол наклона плоскости медленно меняется. Найти зависимость высоты подъема от угла наклона, используя адиабатический инвариант.



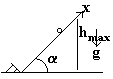
Полная энергия частицы в каждый момент времени равна

E = p²/2m + mgxsinα,

где ось x направлена вдоль наклонной плоскости. С другой стороны, эта же энергия равна потенциальной энергии в точке наивысшего подъема частицы E = mgh_max. Отсюда получаем зависимость импульса от координаты

.

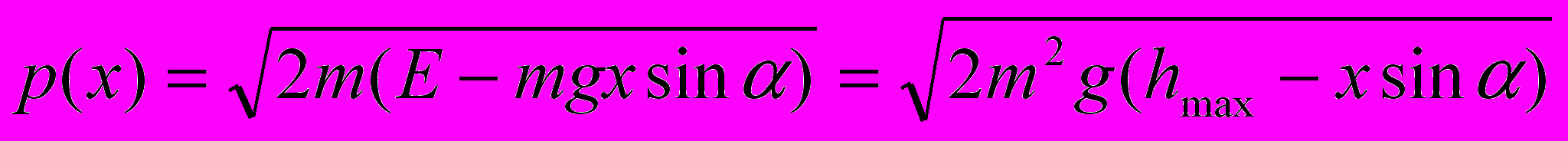Адиабатический инвариант представляет собой интеграл по всему циклу движения, например, от нижней точки до верхней и обратно. Так как угол за один цикл меняется незначительно, то мы можем его считать постоянным. По той же причине постоянной будет и полная энергия.

Интеграл 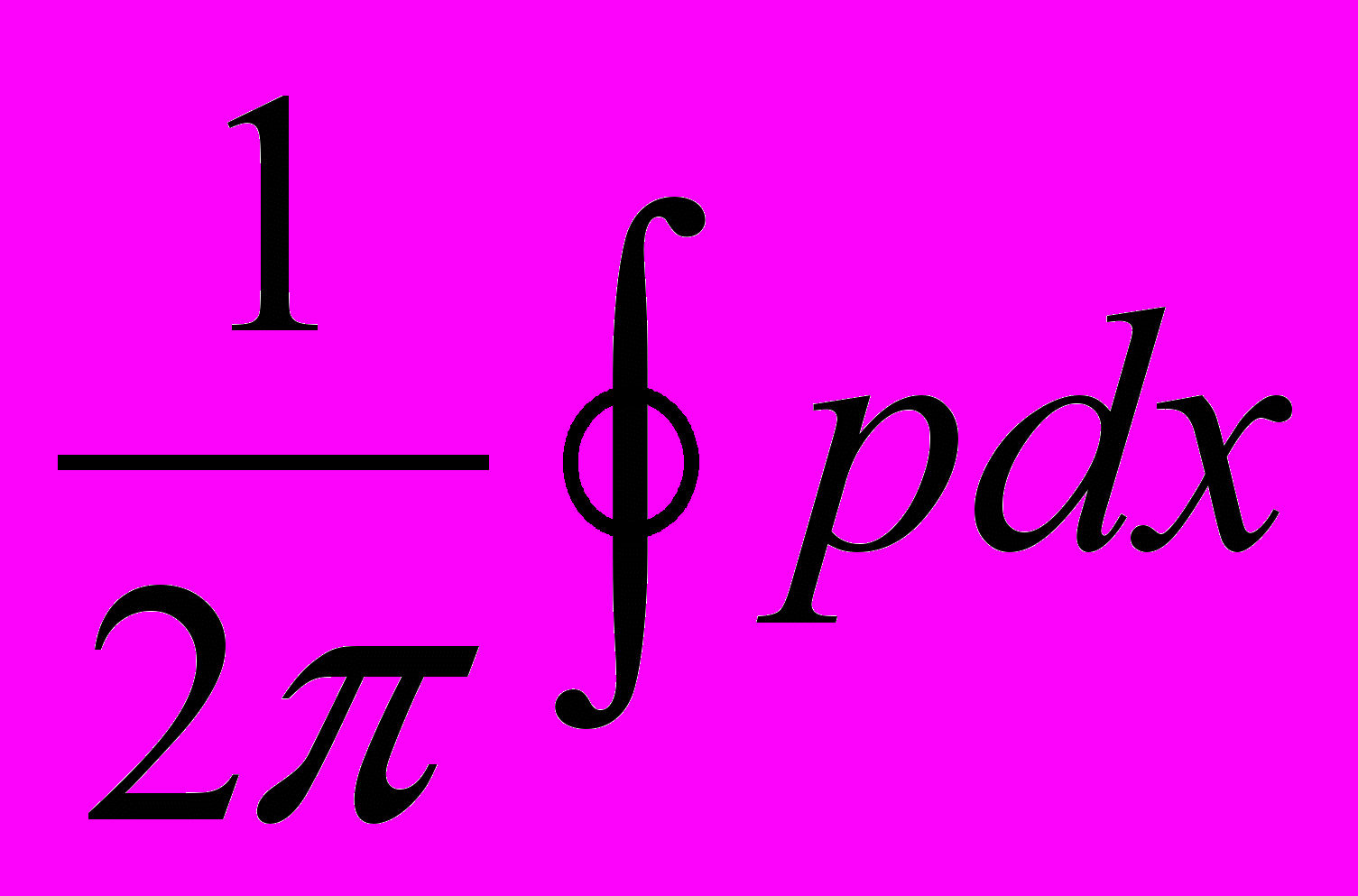по всему циклу равен удвоенному интегралу по движению от нижней точки до верхней, то есть величине

.

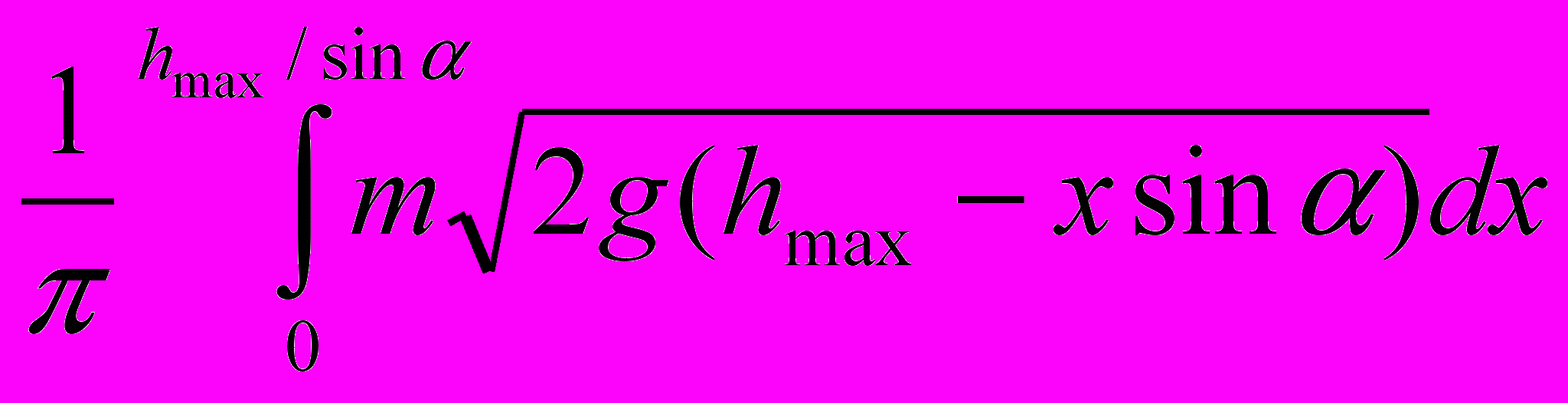Обозначив u = xsinα/h_max и произведя замену переменной интегрирования x на u, получим

.

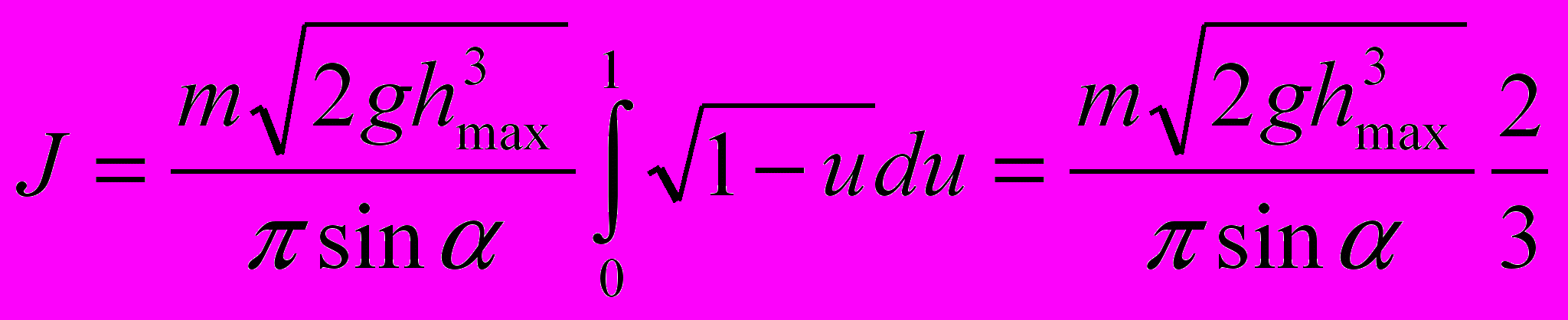Так как эта величина остается постоянной в процессе медленного изменения угла наклона α, то максимальная высота подъема изменяется по закону

.
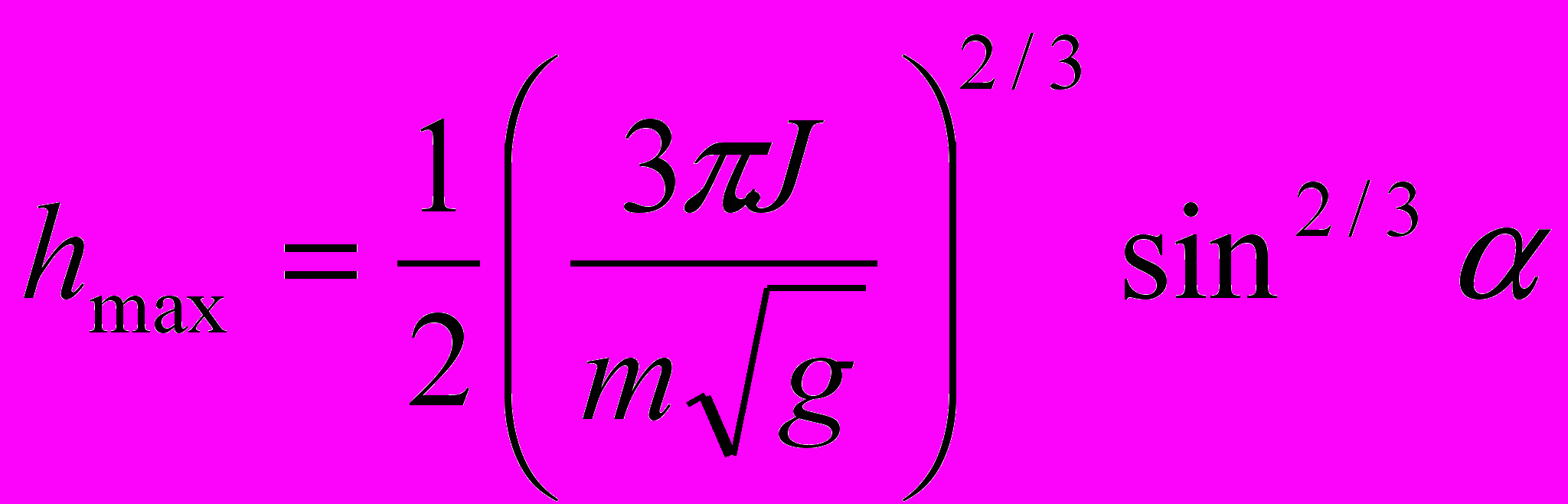