Курсовая работа по дисциплине «земельный кадастр» на тему: «оценка земли и иной недвижимости»

Вид материала

Курсовая

Содержание Глава 2. Методы оценки рыночной стоимости недвижимости Глава 3. Отчет об оценке объекта недвижимости Задачи к 1 главе 2-я функция 4-я функция 5-я функция 6-я функция Затратный метод оценки рыночной стоимости недвижимости. Оценка рыночной стоимости недвижимости методом сравнения продаж. Задачи ко 2 главе. Размер вносимых поправок Ответ: Цена торгового центра составляет 111160$.Задача 2.1 Сравнимые объекты Ответ: стоимость участка площадью 0,15 га со всеми коммуникациями кроме газопровода составляет $33830.Задача 2.2. Метод Ринга. Техника остатка для оценки земли АО “Перово” Общие сведения 1. Имя заказчика 3. Дата определения стоимости ... Полное содержание

Подобный материал:

• Задачи землеустройства Государственный земельный кадастр Регистрация земельных участков, 15.64kb.
• Землеустройство и земельный кадастр» ипо специальностям: 310900 «Землеустройство»,, 925.08kb.
• Рабочая программа по дисциплине «Агроландшафтное земледелие» Для специальности: 310900, 307.26kb.
• 120300. 62 Землеустройство и кадастры с профилями специальных дисциплин Земельный кадастр,, 142.77kb.
• Курсовая работа по кафедре политической экономии, 105.07kb.
• Тематика курсовых работ по дисциплине «Оценка и налогообложение недвижимости и другого, 18.49kb.
• «Почвоведение», 616.13kb.
• Очно-дистанционный курс повышения квалификации земельные отношения в российской федерации, 391.37kb.
• Календарный план по Прикладной математике для студентов третьего курса факультетов, 24.64kb.
• Программа профессиональной переподготовки «Оценка стоимости производства (бизнеса)», 393.82kb.

Министерство сельского хозяйства Российской Федерации

Государственный Университет по Землеустройству

Кафедра землепользования и земельного кадастра

КУРСОВАЯ РАБОТА

ПО ДИСЦИПЛИНЕ «ЗЕМЕЛЬНЫЙ КАДАСТР»

НА ТЕМУ: «ОЦЕНКА ЗЕМЛИ И ИНОЙ НЕДВИЖИМОСТИ»


Выполнила: ст. 52 к 2 гр. Тазаев К. Ю.

Проверил: Волклвой


Москва

2005

ОГЛАВЛЕНИЕ

		Стр.
1.	Введение	3
2.	Глава 1. Функции денежной единицы	4
3.	Задачи к 1 главе	8
4.	Глава 2. Методы оценки рыночной стоимости недвижимости	13
5.	Задачи ко 2 главе.	20
6.	Глава 3. Отчет об оценке объекта недвижимости	26
7.	Заключение	47
8.	Библиографический список	48

ВВЕДЕНИЕ.

За последние годы оценка недвижимости выделилась в самостоятельную и относительно обособленную область профессиональной деятельности — одну среди многих новых для России профессий, вызванных к жизни переходом страны от плановой экономики к рыночной. В ноябре 1996 г. Министер­ство труда и социального развития Российской Федерации дало официальное описание профессии «ОЦЕНЩИК (эксперт по оценке имущества)». С этого момента профессию оценщика можно считать официально признанной в России.

Целью оценки является определение текущей рыночной стоимости на объект недвижимости и все, что с ним прочно связано. Под рыночной стоимостью понимается ценность прав на доход и блага, даваемые недвижимостью.

Рыночная стоимость недвижимости как объект оценки может формироваться и развиваться только в условиях функционирования рынка. Для правильного понимания этого понятия и тенденций его развития в главе первой данной курсовой работы будут рассмотрены шесть функций денежной единицы, а также их практическое применение при решении задач.

Во второй главе приводятся методы оценки недвижимости, а также будут решены задачи по оценке с применением этих способов.

Третья глава содержит примерный отчет по оценке объекта недвижимости.

Итак, рассмотрим подробнее вышеуказанные вопросы.


ГЛАВА 1.

Функции денежной единицы.


1-я функция. Накопленная сумма денежной единицы.

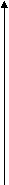Данная функция выражается формулой FV=PV*(1+i)ⁿ , где FV – накопленная сумма (будущая стоимость), PV – текущая стоимость, i – ставка сложного процента, n – срок накопления (в годах). Графическое представление 1-й функции:

FV




время

n n-1 3 2 1 0


2- я функция. Текущая стоимость денежной единицы (реверсия) – обратная FV.

Величина её рассчитывается по формуле: 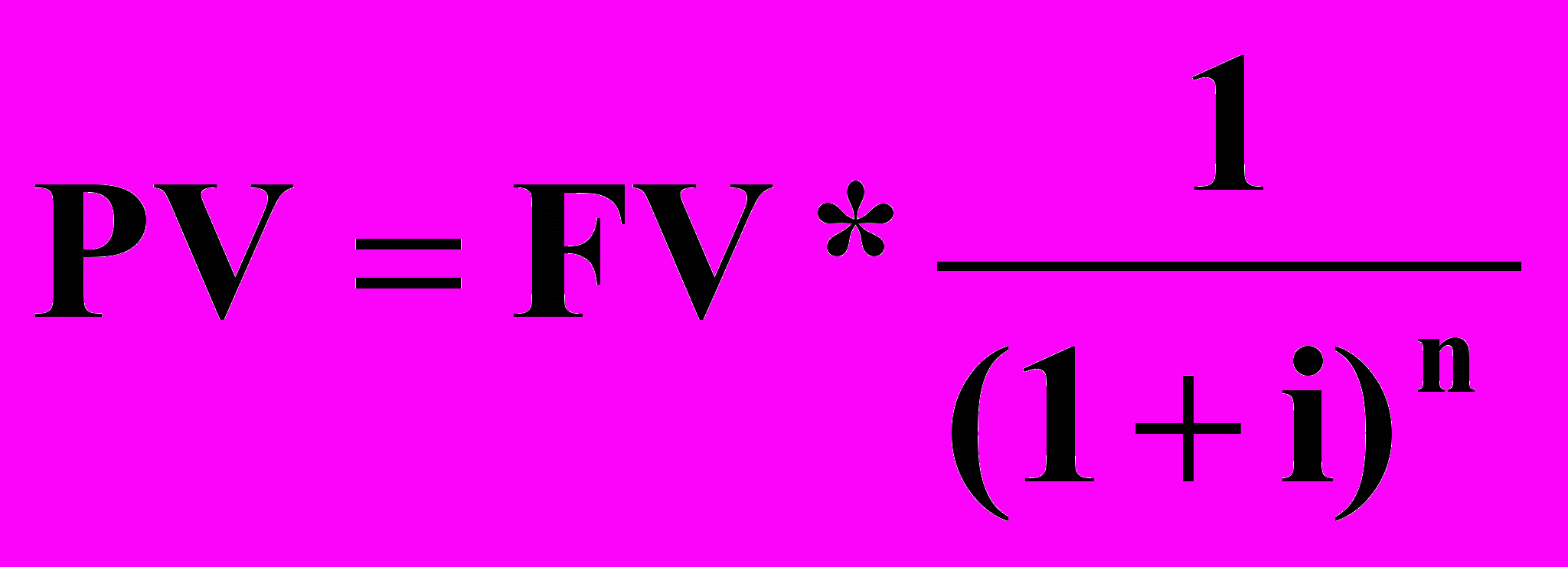- для начислений, осуществляемых 1 раз в год; и по формуле: 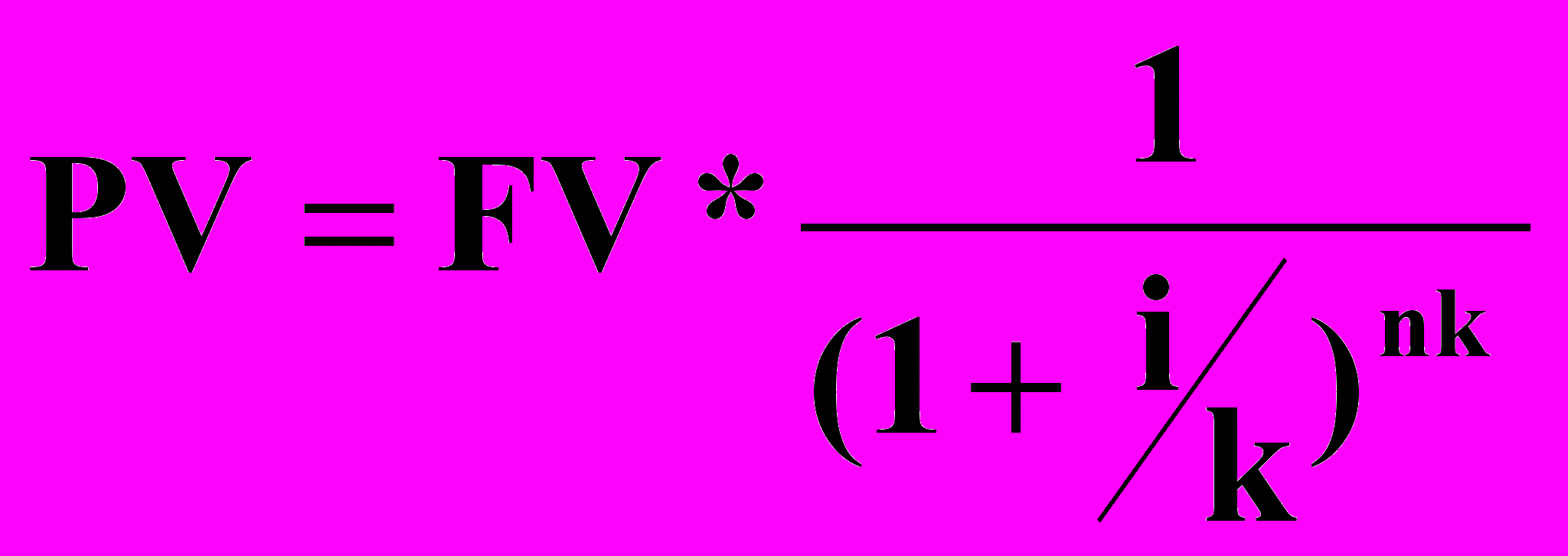- для начислений, осуществляемых чаще одного раза в год (при этом k =12 для начислений, осуществляемых ежемесячно, k =4 для начислений, осуществляемых ежеквартально и k = 2 для полугодичных начислений). Наглядно данную функцию можно представить в виде графика:

FV














время

0 1 2 3 n-1 n


3-я функция. Текущая стоимость аннуитета.

Аннуитет (РМТ) – серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени. Принято различать обычный и авансовый аннуитет.

Если платежи осуществляются в конце периода, имеет место обычный аннуитет. Текущая стоимость обычного аннуитета вычисляется по формуле: .

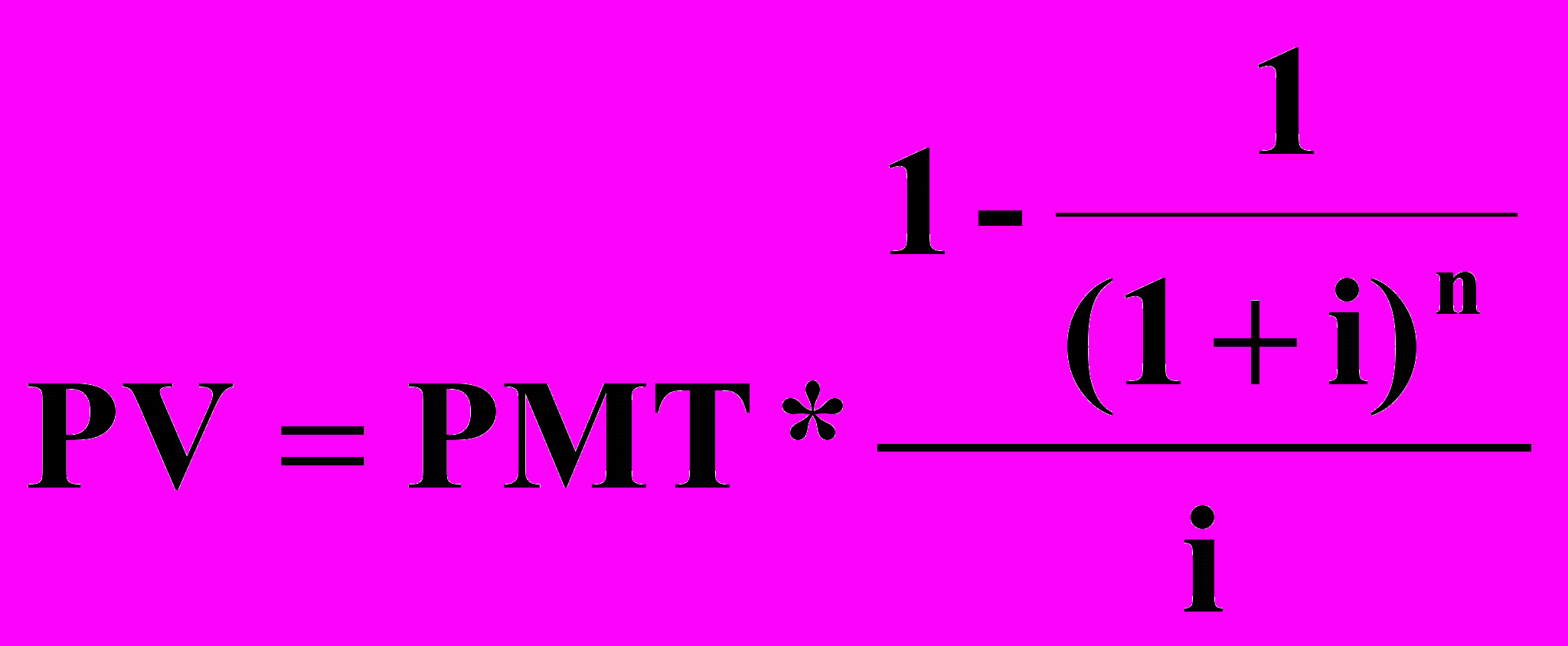Если платежи осуществляются авансом (в начале каждого периода), имеет место авансовый аннуитет. Текущая стоимость авансового аннуитета рассчитывается по формуле:

.

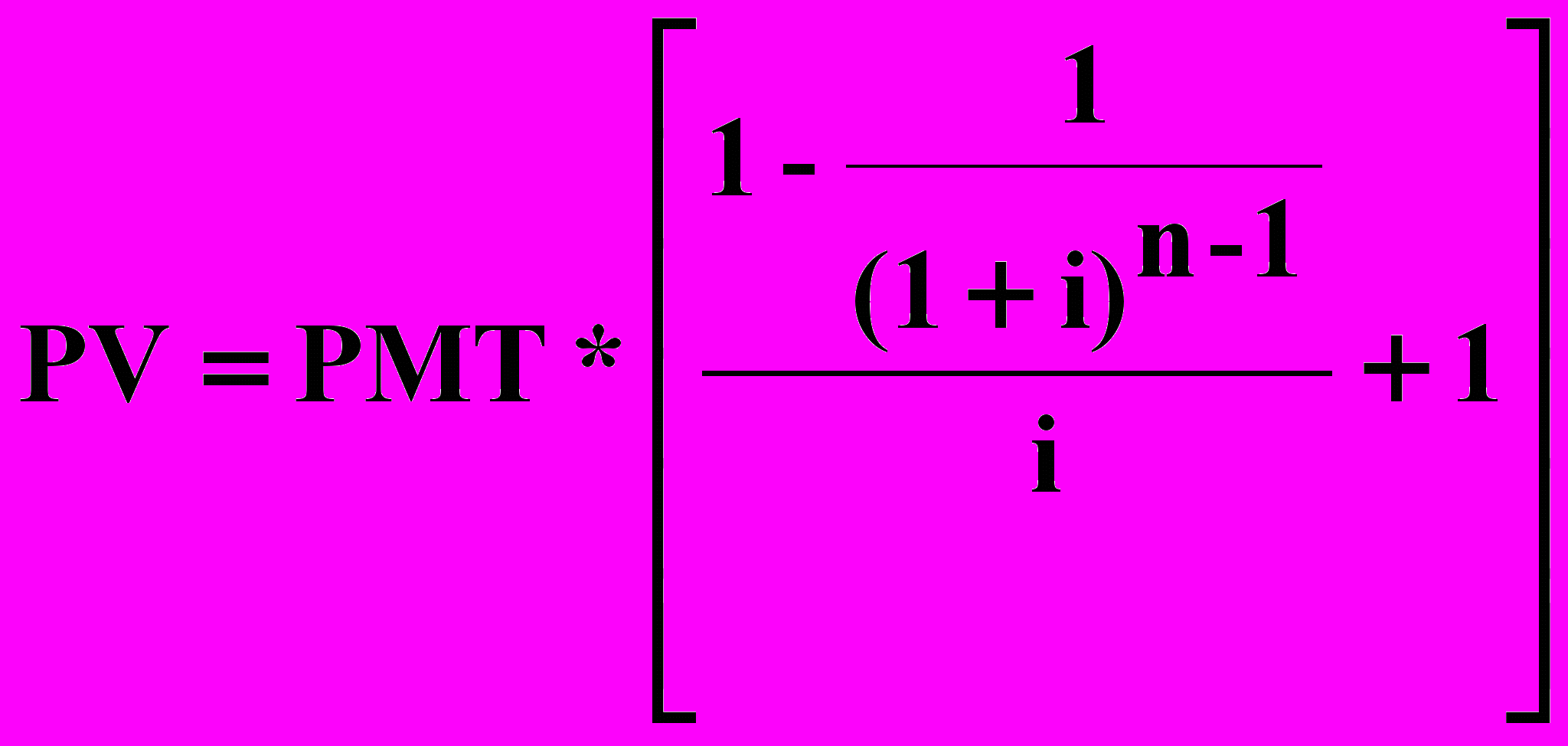В общем виде график данной функции выглядит следующим образом:




PV















время

0 1 2 3 n-1 n


4-я функция. Накопление денежной единицы за период.

На основании использования данной функции определяется будущая стоимость серии равновеликих периодических платежей.

1. Для платежей, осуществляемых один раз в году:

- расчет будущей стоимости обычного аннуитета производится по формуле:

;

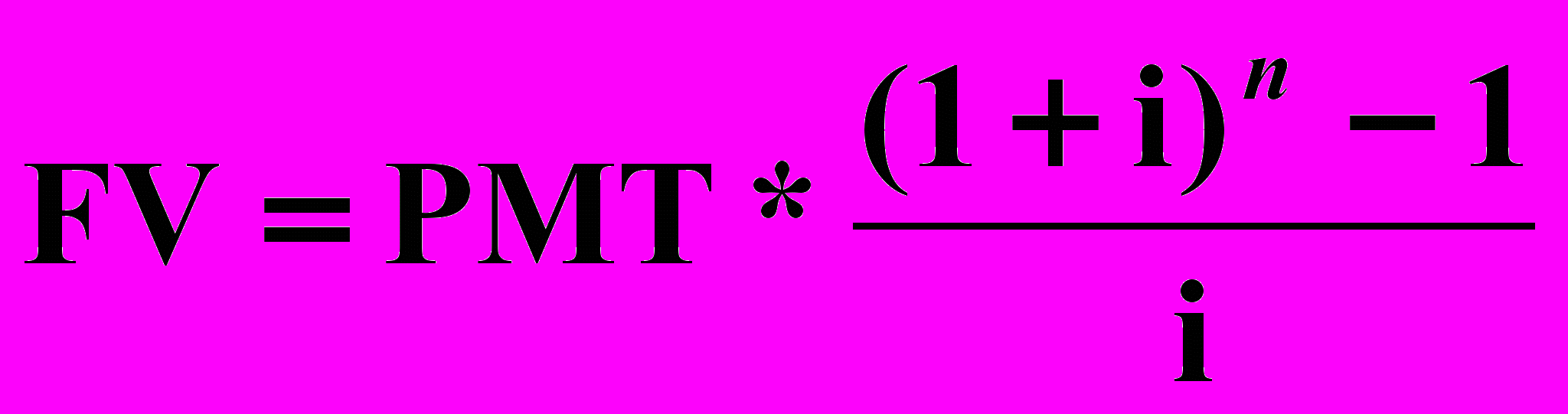- расчет будущей стоимости авансового аннуитета производится по формуле:

.

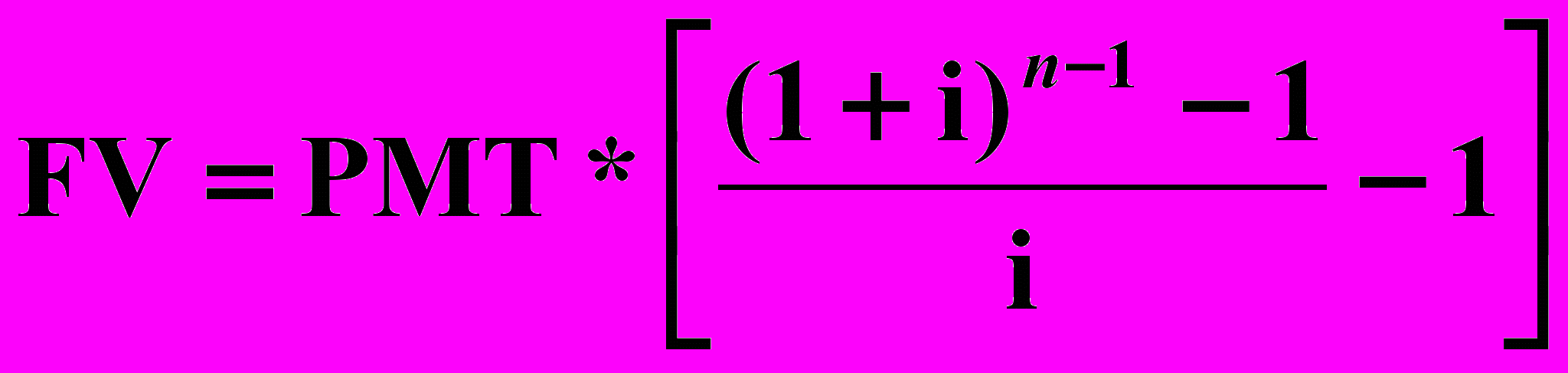2. Для платежей, осуществляемых чаще одного раза в год:

- расчет будущей стоимости обычного аннуитета производится по формуле:

;

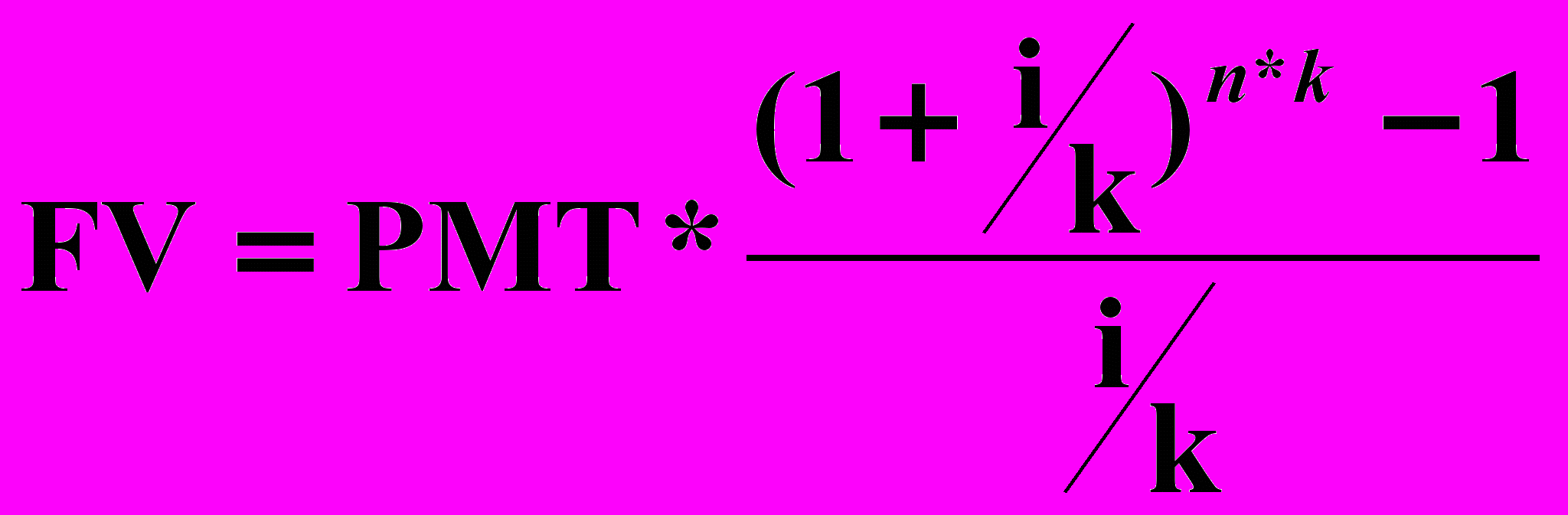• расчет будущей стоимости авансового аннуитета производится по формуле:
  

_.

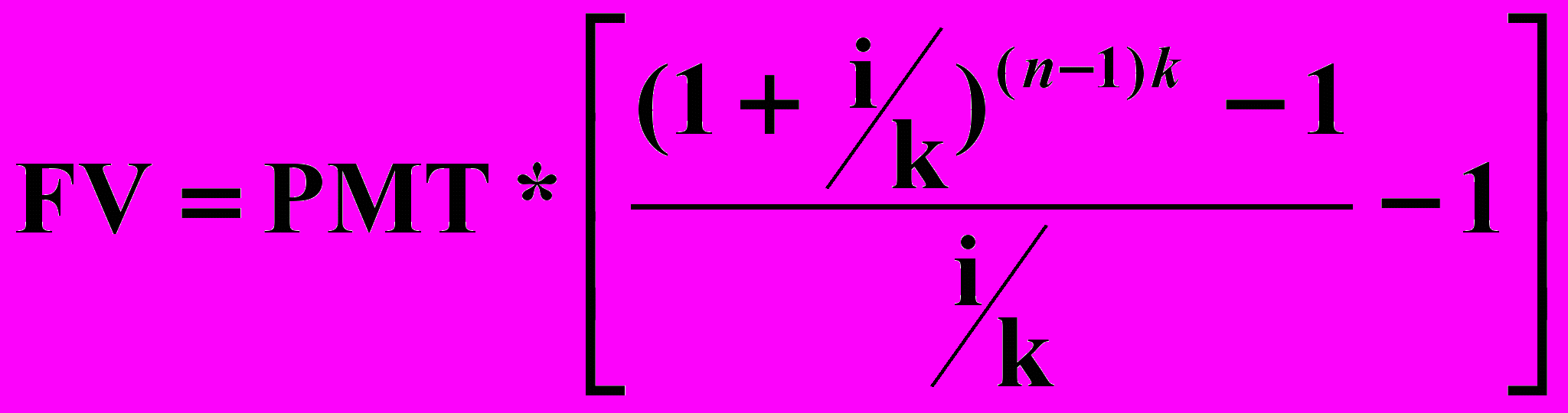График данной функции имеет вид:

а) для обычного аннуитета: б) для авансового аннуитета:

FV FV













время время

0 1 2 3 n-1 n 0 1 2 3 n-1 n


5-я функция. Взнос на амортизацию денежной единицы.

Это равномерный периодический платеж в погашение приносящего доход кредита. Амортизация – процесс погашения долга в течение времени. Величина амортизации денежного долга показывает, каким будет обязательный периодический платеж по кредиту, включающий проценты и выплату основной суммы, позволяющий погасить кредит в течение установленного срока. Каждый платеж состоит из 2-х частей: РМТ = on + of, где on – погашение процента, of – погашение кредита.

Взнос на амортизацию денежной единицы можно определить, используя формулу:

.


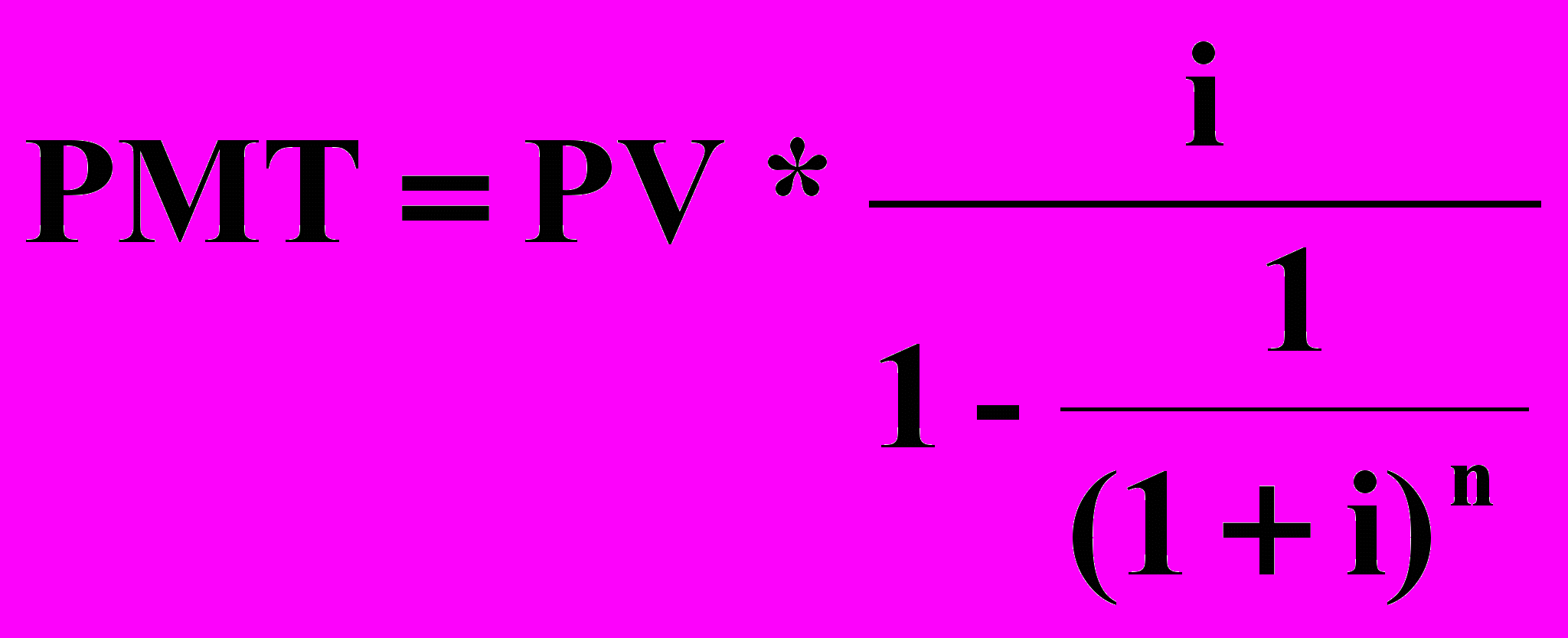График этой функции выглядит следующим образом:

PV


















время

0 1 2 3 n-1 n

6-я функция. Формирование фонда возмещения.

Данная функция используется для определения тех равномерных периодических платежей, которые необходимо осуществить в течение заданного периода, чтобы к концу срока иметь на счете, приносящем доход по заданной ставке, определенную сумму денег. Эта функция обратна 4-й функции – накоплению денежной единицы за период.

Величина указанных платежей находится по формуле:





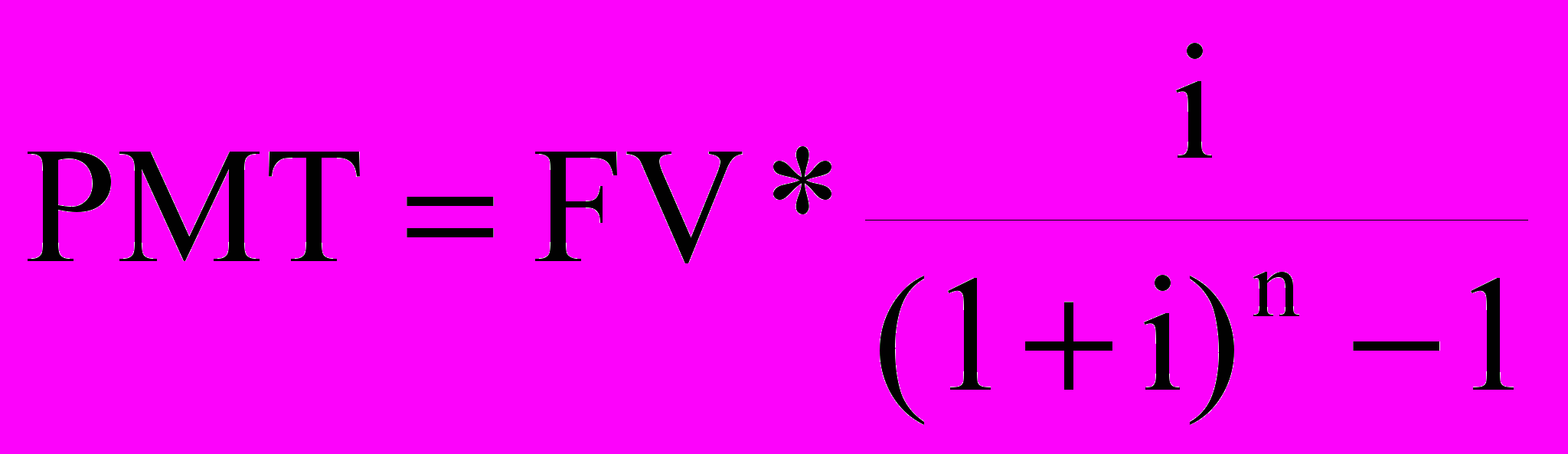
Графически данная функция может быть представлена следующим образом:

FV
















время

0 1 2 3 n-1 n


ЗАДАЧИ К 1 ГЛАВЕ

1-я функция: Накопленная стоимость денежной единицы


Задача 1.

Определить будущую стоимость 500$ через 5 лет при ставке капитализации 8% при условии, что начисление процентов происходит в конце каждого года.


Решение:

PV=500$

n=5 лет

i=0,08

FV-?

Для решения задачи, при условии, что начисление процентов происходит в конце каждого года, используется формула


FV=PV*(1+i)ⁿ


FV=500*(1+0,08)⁵= 734,66$

Ответ:

При начислении процентов в конце каждого года, к концу 5 года будет накоплена сумма в 734,66$.


2-я функция: Текущая стоимость денежной единицы (реверсия).


Задача 2.

Определить текущую стоимость 500$, которые будут получены в конце 5 года при 8%-й ставке дисконта при условии, что начисление процентов происходит в конце каждого года.


Решение:

FV=500$

n=5 лет

i=0,08

PV-?

Для решения задачи, при условии, что начисление процентов происходит в конце каждого года, используется формула







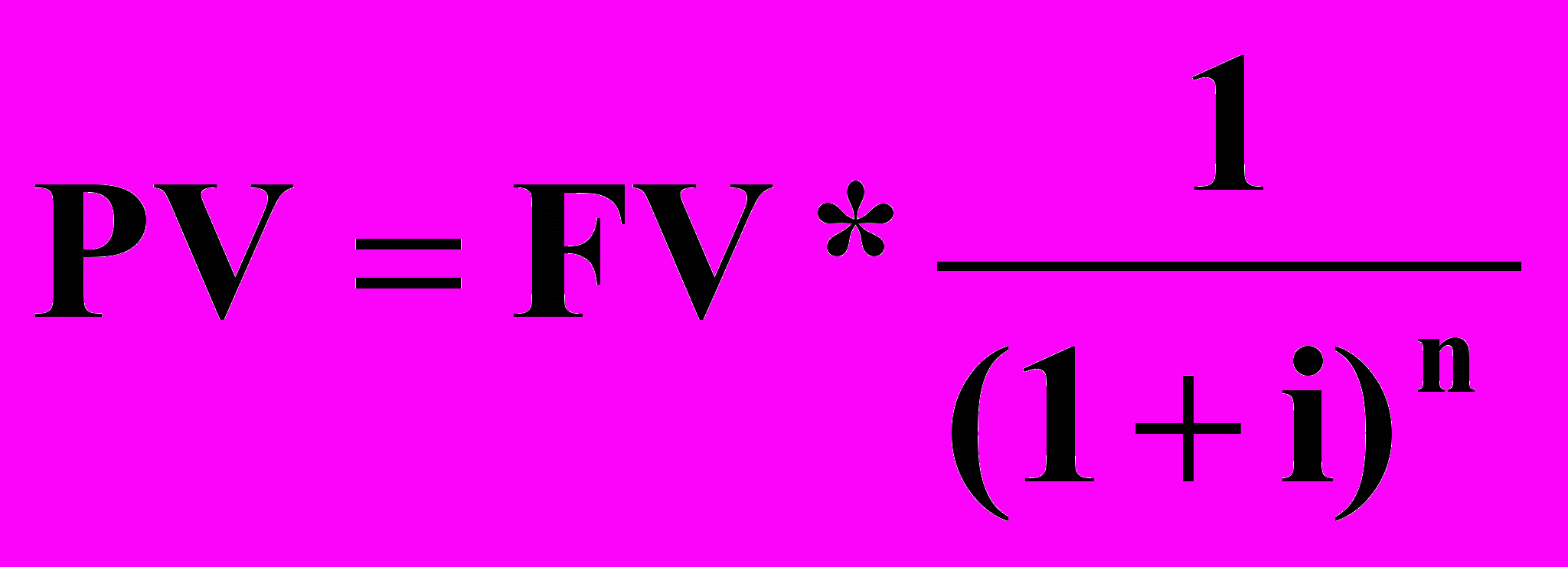
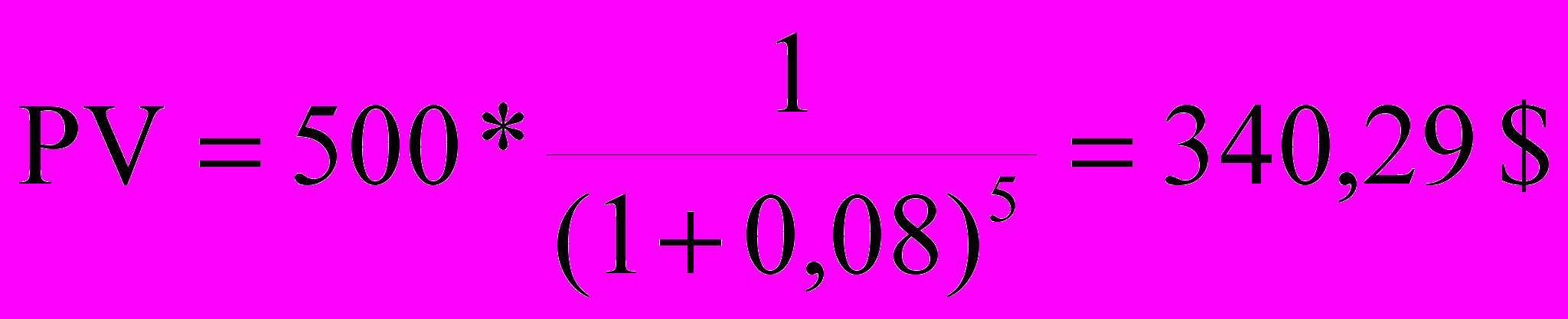
Ответ:

При начислении процентов в конце каждого года, текущая стоимость составит 340,29 $.


3-я функция: Текущая стоимость аннуитета.


Задача 3.

Договор аренды квартиры составлен на 5 лет. Определить текущую стоимость арендных платежей при 8%-й ставке дисконта при условии, что арендная плата 500$ выплачивается в конце каждого месяца.


Решение:

PMT=500$

n=5 лет

i=0,08

k=12

PV-?

Для решения задачи при условии, что арендная плата выплачивается в конце каждого месяца, используется формула







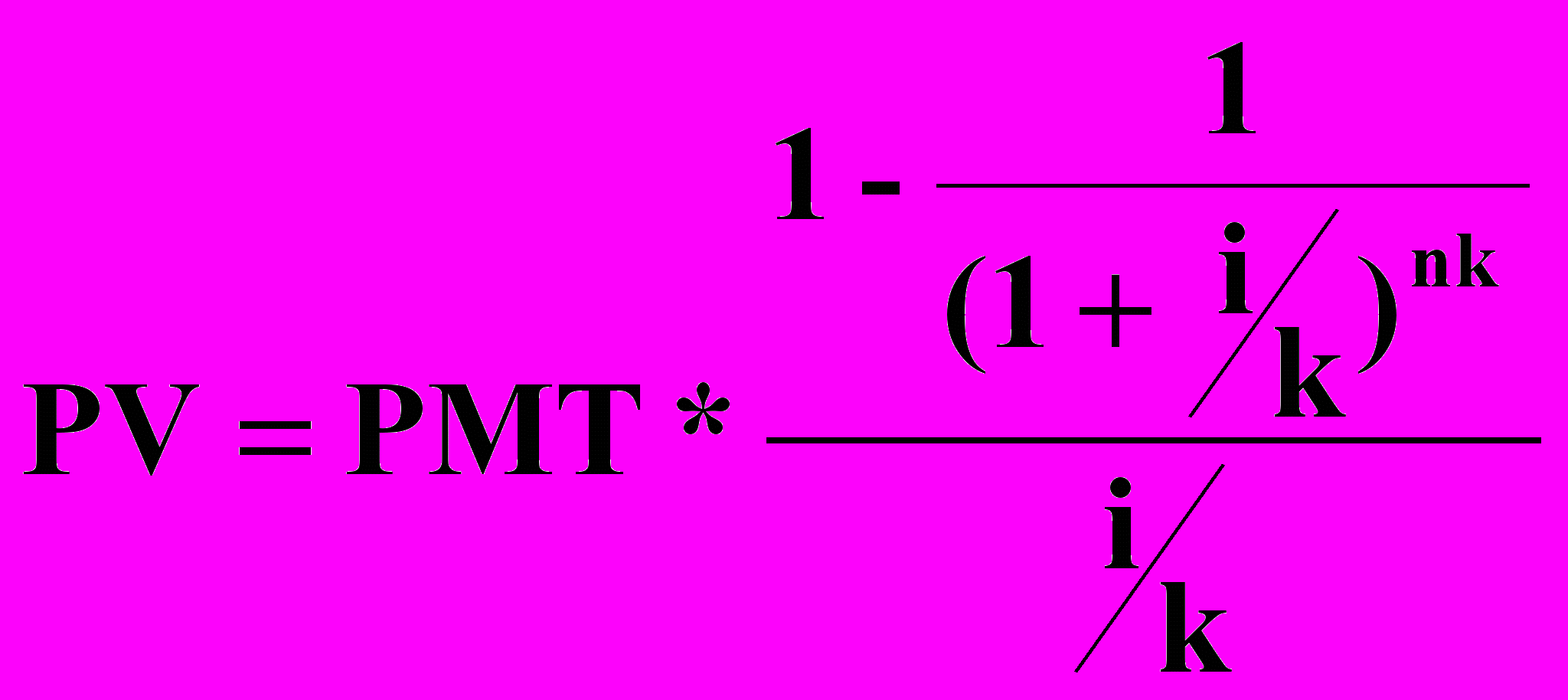
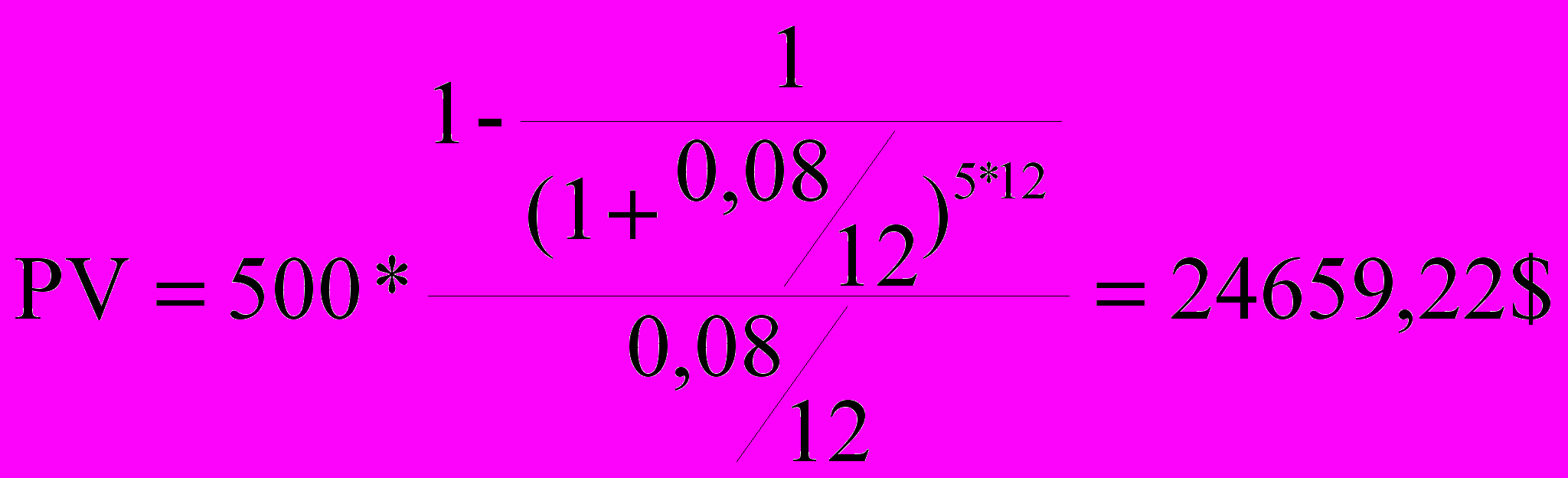
Ответ:

Текущая стоимость арендных платежей при выплате арендной платы в конце каждого месяца составляет 24659,22$.


4-я функция: Накопление денежной единицы за период.


Задача 4.

Определить сумму, которая будет накоплена на счете, приносящем 5% годовых, к концу 3 года, если ежегодно откладывать на счет 500$. Платежи осуществляются в конце каждого года.


Решение:

PMT=500$

n=3 года

i=0,05

PV-?

Для решения задачи при условии, что платежи осуществляются в конце каждого года, используется формула:







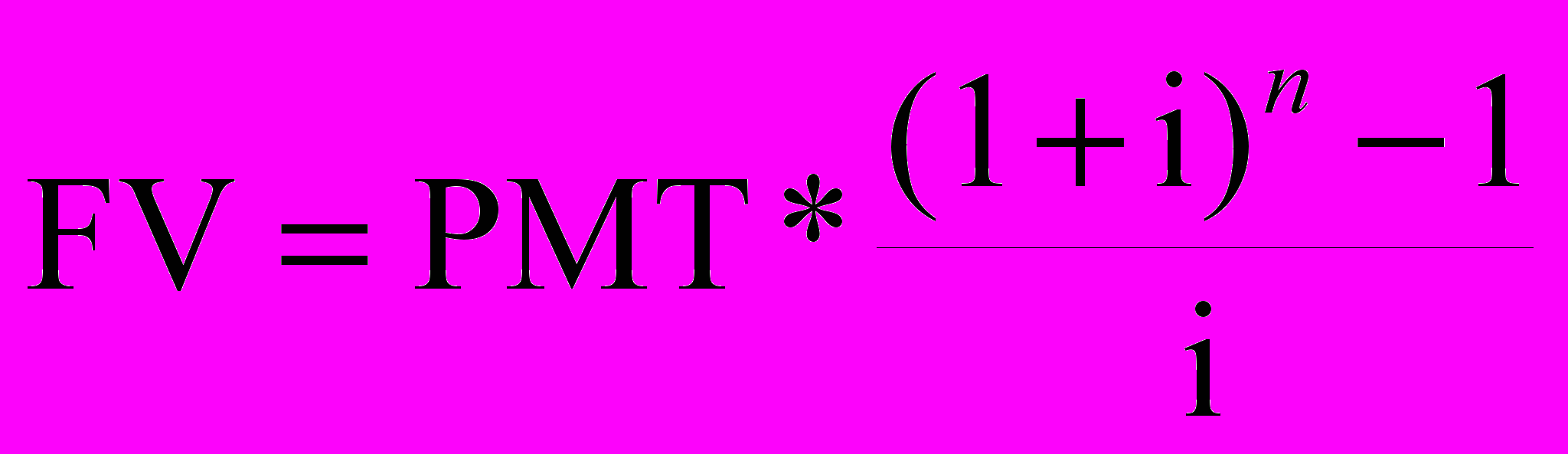
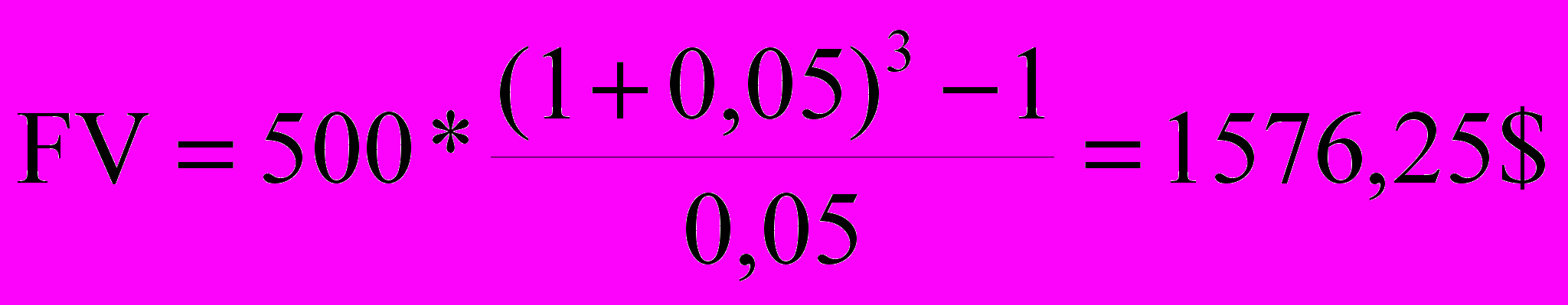
Ответ:

К концу 3 года при осуществлении платежей в конце каждого года на счете будет накоплено 1576,25 $.


5-я функция: Взнос на амортизацию денежной единицы.


Задача 5.

Кредит в размере 1000$ выдан на 6 лет под 8% годовых, погашение ежегодное. Определить размер аннуитетных платежей при условии, что выплаты производятся в конце каждого года.


Решение:

PV=1000$

n=6 лет

i=0,08

PMT-?

Для решения задачи, при условии, что выплаты производятся в конце каждого года, используется формула:








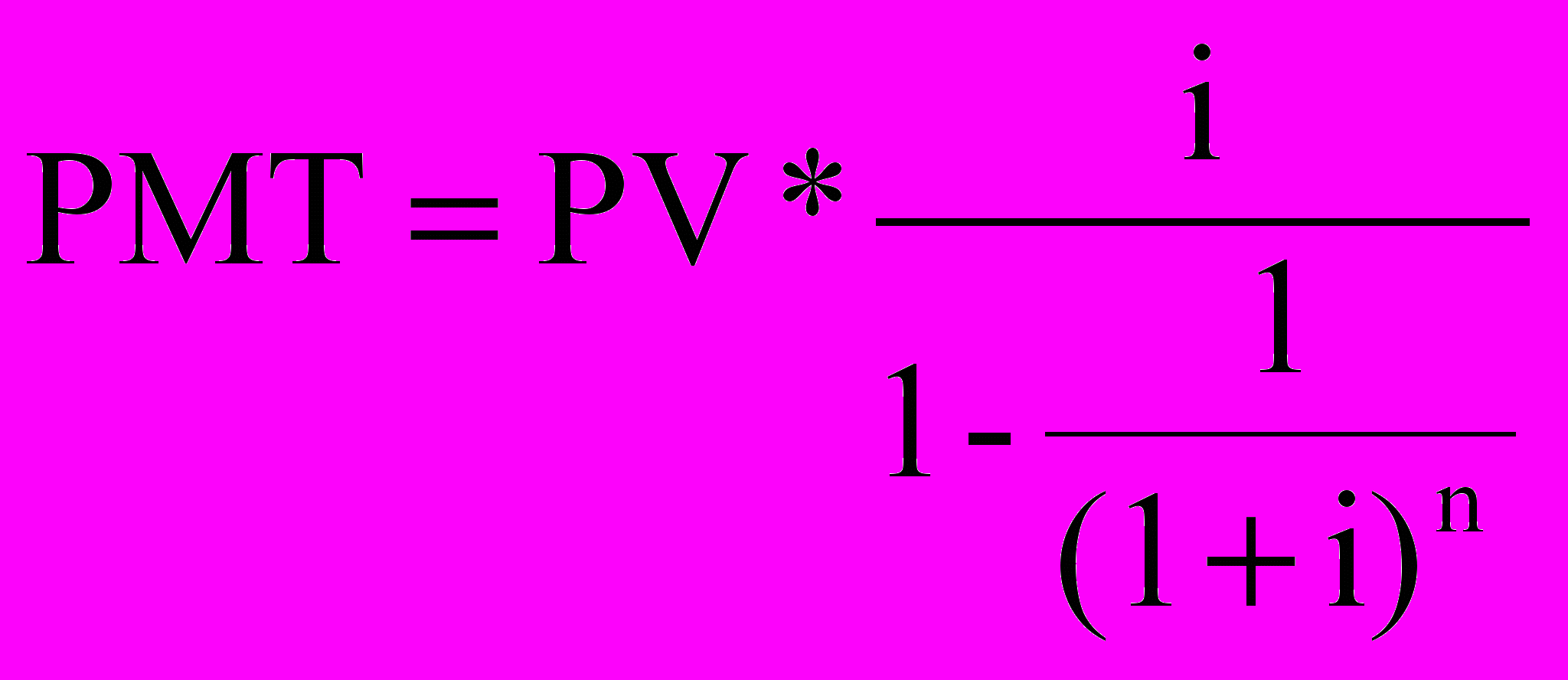
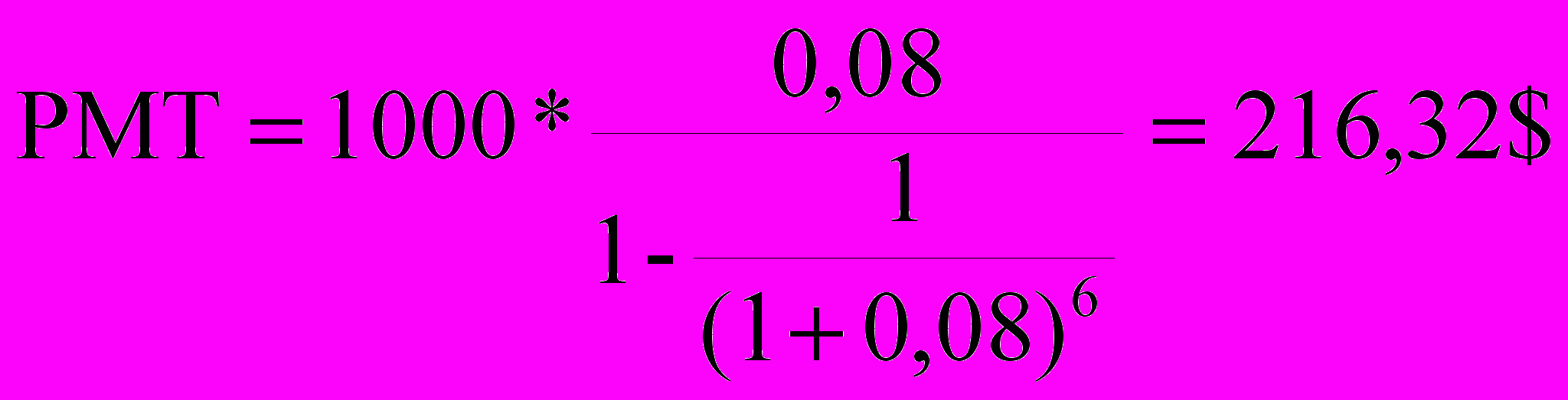
Ответ:

Размер аннуитетных платежей при условии, что выплаты производятся в конце каждого года, составляет 216,32$.


6-я функция: Формирование фонда возмещения.


Задача 6.

Определить, какими должны быть платежи, чтобы к концу 10 года иметь на счете, приносящем 15% годовых, 15000$. Платежи производятся в конце каждого года.


Решение:

FV=15000$

n=10 лет

i=0,15

PMT-?

Для решения задачи при условии, что платежи вносятся в конце каждого года, используется формула:







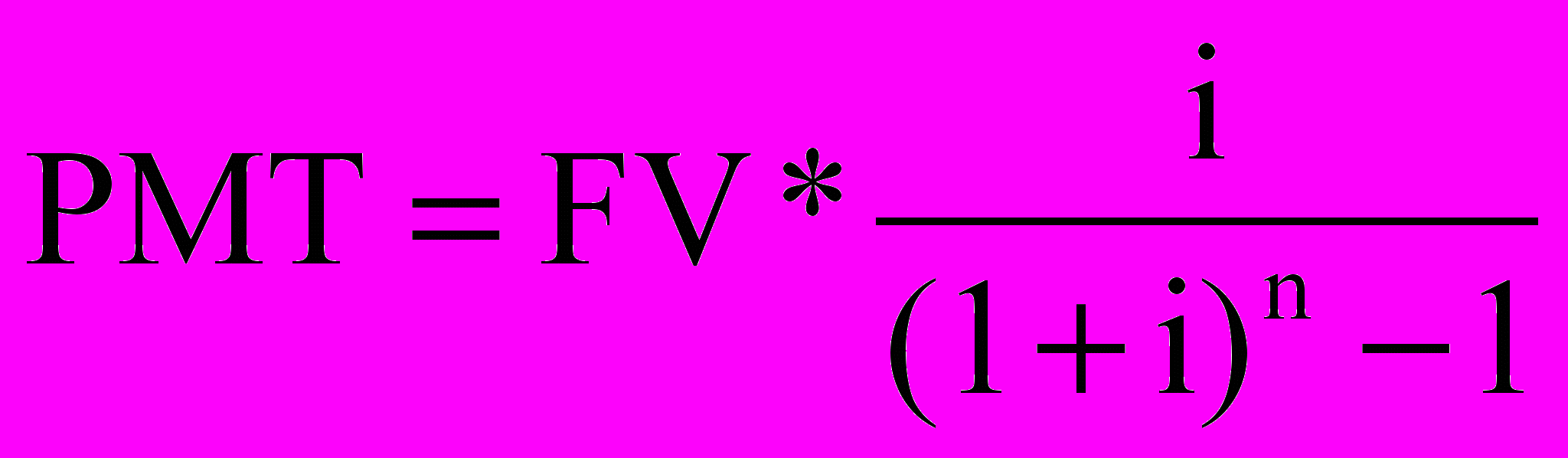
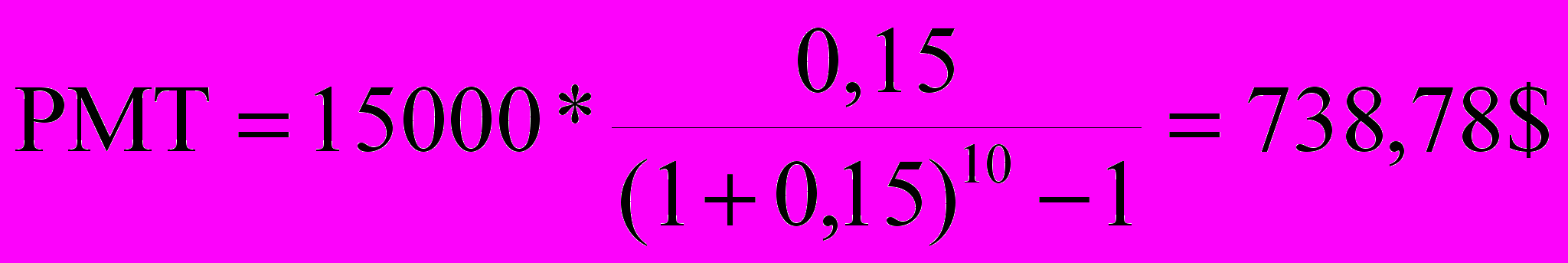
Ответ:

Платежи, вносимые в конце каждого года, составляют 738,78$.


ГЛАВА 2.

Методы оценки рыночной стоимости недвижимости.

При оценке рыночной стоимости недвижимости применяются три стандартных метода:

• затратный метод;
  
• метод сравнительного анализа продаж;
  
• доходный метод (метод капитализации дохода).
  

В общем случае при наличии достаточного количества рыночной информации для оценки необходимо применять все три метода. Невозможность или ограничения применения какого-либо из методов должны быть обоснованы в отчете об оценке.

Рассмотрим подробнее каждый из методов.