Geum.ru

Cols=2 gutter=24> 2004/№3 Засновники

Вид материалаДиплом

Содержание


Наприклад, такі вправи пропоную на розвиток уміння розпізнавати форму цифр.
Оксана Пянило
Подобный материал:
1   ...   4   5   6   7   8   9   10   11   ...   21

Наприклад, такі вправи пропоную на розвиток уміння розпізнавати форму цифр.


1. Які цифри ви бачите на малюнках? Напишіть їх.



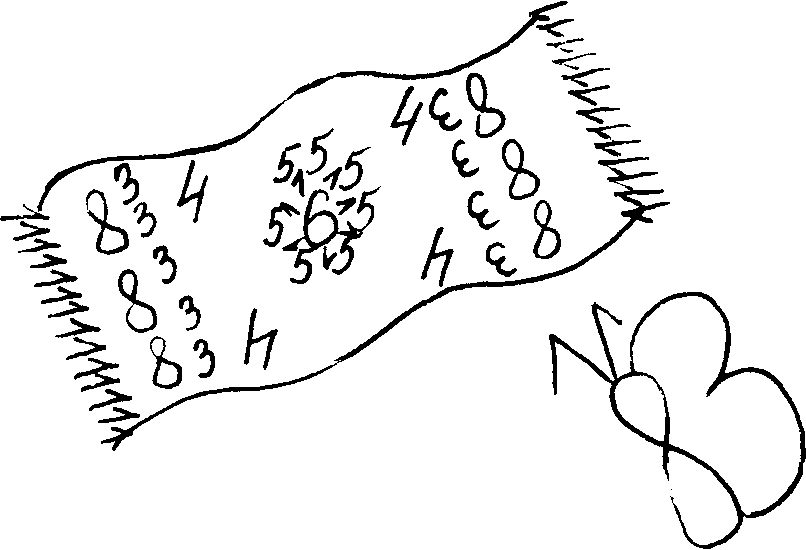
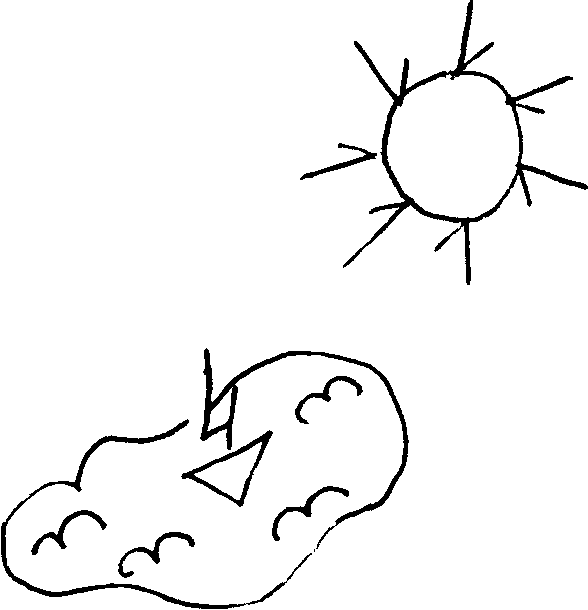
2. Напишіть цифру, яка схожа на гуску.

3. Яка цифра нагадує форму яйця?

4. Назвіть цифри, які схожі на ці предмети:








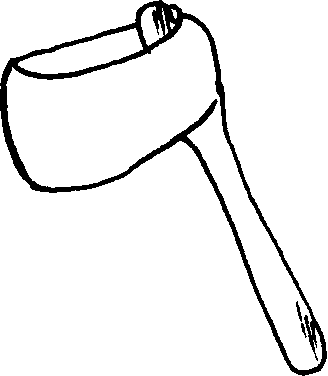
Широко практикую на уроках відгадування ребусів, загадок, шарад. Школярі залюбки заучують віршовані лічилки, розв'язують римовані задачі.

Наприклад, при вивченні цифри 5 зачитую дітям вірш, після чого вони ознайомлюються і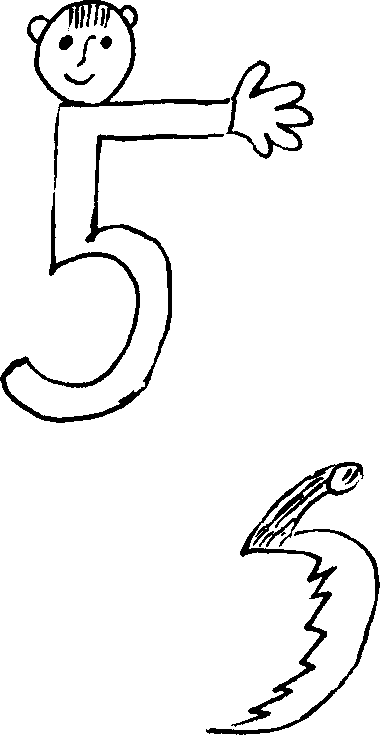з виглядом цифри і характеризують її.

Ось і вийшла погулять

На папері цифра п'ять,

Руку вправо протягнула

Ніжку бубликом зігнула.

На що схожа цифра п’ять?

На серп, звичайно, як не знать!


Увесь цей набір нестандартних вправ у комплексі зі звичайними сприяє розвитку уваги, спостережливості, логічного мислення, математичного мовлення, стимулює інтерес до математики.

В математичній освіті учнів особливе місце займають задачі. З одного боку вони складають специфічний розділ програми, а з другого – виступають як дидактичний засіб навчання, виховання і розвитку школярів.

Задачі виконують свої дидактичні функції за умови, що учні набудуть певних уявлень про їхню сутність і оволодіють уміннями їх розв’язувати. Цього можна до-сягти формуванням у школярів уявлень про структуру простої і складеної арифметичних задач; ознайомленням з різними способами їх розв’язування, ознайомленням з арифметич-ними діями, залежністю між величинами, а також ознайомленням з формами запису їх розв’язування.

Для активізації розумової діяльності на уроках практикую використання проблемних ситуацій.

Наприклад, при вивченні теми „Задача. Розв’язування задач на знаходження суми й остачі”, ставлю перед дітьми таке завдання:

“ Діти, ось у мене коробка з п’ятьма олівця-ми, а на столику стоїть склянка. Я покладу у склянку два олівці з коробки. Яке запитання ви поставили б про олівці, що знаходяться у коробці?”

Висловлюючи свої думки, діти вибирають правильне запитання, розв’язують задачу та роблять висновок (Орієнтовний висновок: задача складається з умови, запитання, розв’язку і відповіді ).

Для закріплення даного поняття пропо-ную роботу в групах, у яких з допомогою наочності діти складають свій варіант задачі, демонструють її іншим дітям і спільно розв’язують. Така робота заохочує дітей до творчого пошуку.

При вивченні елементів геометрії добираю такі завдання, щоб зацікавити дітей і сприяти розвиткові просторових уявлень, образного мислення. Наприклад:
  1. Накресли довільний чотирикутник. Вимі-ряй і запиши довжини його сторін.
  2. Накресли кілька довільних фігур і знайди суму довжин їх сторін. На основі фігур склади малюнок.
  3. Довжина однієї сторони прямокутної ділянки 16 м, а друга на 24 м довша. Знайти довжину паркану, який треба побудувати по межі цієї ділянки.
  4. Із 13 однакових квадратиків зі стороною 1см склади два рівні квадрати. Яку довжину матимуть сторони цих квадратів?

Загальним методичним прийомом, який забезпечує міцні геометричні знання і розвиток просторових уявлень є безпосереднє сприймання учнями матеріальних моделей геометричних образів. Крім розв’язування готових задач, пропоную учням самостійно складати подібні задачі, використовувати знання про геометричні фігури на уроках трудового навчання.

При формулюванні поняття величини показую реальний зв’язок математики з життям. Учні вчаться на практиці вимірювати величини, використовувати співвідношення між ними.

Наприклад, ознайомлюючи дітей із поняттями час, міра часу – секунда, хвилина, доба, тиждень, рік, століття, ми виготов-ляємо разом годинники, колекціонуємо кален-дарі. Я підбираю такі завдання, щоб за-цікавити учнів і активізувати їхню діяльність. Перші задачі на час розв’язуємо за допомо-гою годинникового циферблату. Подобається учням завдання, коли вони один одному пропонують назвати годину, яка є на їхньому годиннику.

Початковий курс математики містить елементи алгебри. Вивчення їх у початкових класах сприяє узагальненню знань учнів про число, арифметичні дії і відношення. Школярі одержують початкові відомості про матема-тичні вирази, числові рівності і нерівності, ознайомлюються з буквеною символікою, розв’язують задачі з буквеними даними, у них формується перше уявлення про функціо-нальну залежність. Завдання для вивчення усіх понять стараюся подавати в ігровій формі, із залученням казкових героїв.

Наприклад, при ознайомленні з поняттям “рів-няння” пропоную учням таку ігрову ситуацію:

Білочка знайшла дві шишки і стало в неї 5. Скільки білочка мала шишок?

 + 2 = 5, позначимо невідоме число Х і отримаємо зовсім нову рівність –

х + 2 = 5. Як вона називається? А сорока нам допоможе, вона із лісової школи прилетіла, де звірята теж вивчали таку тему. Давайте хором прочитаємо назву нашої рівності. (Орієнтовна відповідь: рівняння )

Вчу, щоб діти самі формулювали правила, розповідали один одному, адже те, про що дитина зробить власний висновок, надовго їй запам’ятається.

Готуючись до розкриття кожної теми, я ставлю перед собою мету зацікавити і залучити всіх дітей до роботи. Радісно, коли немає нудьгуючих облич, неуважних поглядів. Тому уроки будую так, щоб учні мали змогу зіставляти, порівнювати, шукати і знаходити істину.

Кожна дитина – неповторний світ. Тож дуже важливо відчути її індивідуальність, відшукати ті методичні форми, що сприятимуть збагаченню і розвитку творчого потенціалу, розкриттю здібностей школяра, стимулюватимуть бажання і вміння вчитися. Так діти вчаться відчувати радість пізнання. Тому вважаю, що урок – це дослідницька лабораторія, де вчитель і учень стають свідками великої педагогічної таємниці, коли народжується творчість дитини, активізується її пізнавальна діяльність.

Моделюючи кожен урок, передбачаю відгук учнів на матеріал, що вивчається. Хочеться, щоб діти сприймали математику як спосіб набуття практичного досвіду, щоб відчували насолоду відкриття, щоб у них пробуджувалося бажання знати і творити. Намагаюся так організувати навчання, щоб на уроці працювала не тільки дитяча думка і пам’ять, а й з’являлося натхнення, а це спонукає добирати завдання із проблемними ситуаціями, бо вони збуджують найваж-ливішу рушійну силу розумової активності і саме тоді відбувається перехід від досягну-того рівня знань і розумового розвитку на нову сходинку, на яку треба піднятися у процесі оволодіння новими знаннями.



Література
  1. Богданович М., Виняєва Т., Шарапова Л. Математика в 3 класі. – К.: Радянська школа, 1988. – 144 с.
  2. Богданович М., Козак М., Король Я. Методика викладання математики в початкових класах: Навчальний посібник. – 2-е вид., перероб. і доп.– Тернопіль: Навчальна книга – Богдан, 2001. – 368 с.
  3. Друзь Б. Творчі вправи з математики для початкових класів: Посібник для вчителів. – К.: Радянська школа, 1988. – 144 с.
  4. Контроль та оцінювання навчальних досягнень учнів початкової школи: Методичні рекомендації. // Початкова освіта . – 2002. – № 39-40.
  5. Лісневич Т. Задачі-вірші на уроках математики у молодших класах.– Тернопіль.: Мандрівець, 1997. – 32 с.
  6. Лісневич Т. Цікаві задачі. – Тернопіль.: Мандрівець, 1997. – 48 с.
  7. Cавченко О. Я. Дидактика початкової школи. – К.: Генеза, 2002. – 368 с.
  8. Савченко О. Розвивай свої здібності. – К.: Освіта, 1998. – 160 с.
  9. Савченко О. Умій учитися. – 2-ге вид. – К.: Освіта, 1998. – 192 с.
  10. Савченко О. Сучасний урок у початкових класах. – К.: Магістр – S,1997. – 256 с.
  11. Скрипченко О., Богданович М., Заїка А., Шпакова В. Програма з математики для початкової загальноосвітньої школи. //Початкова школа. – 2003. – №9. – С. 54-60.
  12. Шарапова та інші. Навчання в 3 (2) класах: Посібник для вчителя. – К.: Освіта, 1995. – 296 с.

Оксана Пянило