Xxxv научно-практическая конференция сборник тезисов
| Вид материала | Документы |
- Школьная научно-практическая конференция (сборник материалов), 427.17kb.
- Школьная научно-практическая конференция (сборник материалов), 666.22kb.
- Пятая научно-практическая конференция школьников «Юные дарования 21 века» (сборник, 2167.72kb.
- Xxxv научно-практическая конференция донская академия наук, 2302.6kb.
- Городская открытая научно-практическая конференция старшеклассников по экономике, 49.41kb.
- Международная научно-практическая конференция посвященная, 48.65kb.
- Vi республиканская научно-практическая конференция, 79.16kb.
- Ii международная научно-практическая конференция, 407.62kb.
- Международная научно-практическая конференция «психолого-педагогическое сопровождение, 39.28kb.
- Международная научно-практическая конференция 18-20 октября 2006, 66.74kb.
Анализ амплификаций в поэме С. Есенина
«Черный человек».
^ Розова Яна, 11 кл., МОУ ВСОШ № 5, г. Ростов-на-Дону.
Руководитель: Кривошапко Светлана Александровна, учитель русского языка и литературы, МОУ ВСОШ № 5, г. Ростов-на-Дону.
Актуальность данного исследования в том, что в работах критиков и литературоведов имеет место анализ некоторых тропов и фигур в лирике Есенина, но ни одна работа не предлагает целостного анализа особых средств усиления изобразительности – амплификаций.
Цели данной работы: определить роль амплификаций в поэме С. Есенина «Черный человек»; изучить своеобразие есенинских амплификаций в данном произведении.
Задачи: проанализировать лексический состав амплификаций в поэме «Черный человек»; рассмотреть некоторые грамматические категории, наиболее ярко проявившиеся как стилеобразующее средство; установить круг образов и лейтмотивов, связанных с амплификациями в поэме Есенина.
Методы исследования: сплошная выборка при извлечении материала; описание, сопоставление, стилистический анализ.
Основным приемом организации образной системы поэмы является, на наш взгляд, прием «двойничества», который организуется посредством двух художественных образов поэмы – образа лирического героя и образа Черного человека. Сущность приема двойничества заключается в двуплановости связей между ключевыми образами поэмы: противопоставление и отталкивание; соотнесение и объединение. Автор организует эту двуплановость связей при помощи фигуры парадиастолы.
Для реализации этого приема поэт использует символ – зеркало. Являясь традиционным в русской национальной культуре и литературе, этот символ в поэме «Черный человек» подвергается переосмыслению и индивидуальной интерпретации.
Принципу противопоставления и объединения одновременно соответствуют и образные средства, использованные в поэме. Наряду с амплификациями, основанными на контрасте (антитеза, оксюморон) используются и амплификации, основанные на тождестве языковых единиц. Поэме свойственна особая система плеоназмов – повторение слов (черный, черный; очень и очень); синонимов (прохвост и забулдыга; в грозы, в бури), а также целых четверостиший (например, первое четверостишие «Друг мой, друг мой…» повторяется два раза).
Кажущиеся парадоксальными противопоставления и сопоставления создают в поэме резкие эмоциональные контрасты, способствуют выражению особого драматизма, остроты чувств.
Исследование амплификаций в поэме С. Есенина можно использовать в дальнейшем при изучении особенностей стиля языка поэта, в спецкурсах по творчеству Есенина, риторике.
^ Развитие классических традиций русской лирики
в творчестве Николая Рубцова. Перекличка лирики
Н. Рубцова с поэзией Ф. Тютчева, А. Фета, С. Есенина
Лапицкая Людмила, 9 кл., МОУ СОШ № 52, г. Ростов-на-Дону.
Руководитель: ^ Белоусова Татьяна Викторовна, учитель русского языка и литературы, МОУ СОШ № 52, г. Ростов-на-Дону.
Цели представляемой работы: рассмотреть поэтическое наследие Николая Рубцова в свете развития русской классической традиции, проанализировать основные темы творчества Николая Рубцова (природа, одиночество, тема души, деревни, Родины) в контексте тютчевско-фетовско-есенинской традиции.
Основная доказываемая гипотеза: в ранней лирике поэта ярко выразилась есенинская традиция, которая проявилась, прежде всего, в стихотворениях о русской деревне и природе. Муза Есенина помогла Рубцову самоопределиться в современности, поэтически осмыслить свою глубинную связь с родной землёй. Зрелые стихотворения Николая Рубцова также содержат отпечаток традиции Есенина, но мироощущение поэта становится все ближе к поэтическим мироощущениям Тютчева и Фета.
Методы исследования заявленной проблемы: изучение различных печатных изданий, сборников стихотворений Н. Рубцова, С. Есенина, Ф. Тютчева и А. Фета, работа с различными СМИ, Интернет-ресурсами.
Ранние стихотворения Н. Рубцова еще носят в чем-то подражательный характер, но уже в них сказывается приверженность поэта к традициям устного народного творчества и русской классической поэзии, желание творчески развить завещанное предшественниками. В зрелом периоде творчества происходит углубление философской проблематики, широкое использование символики, классического жанра элегии. Особенно плодотворным стало обращение к опыту Ф. Тютчева и А. Фета. Творчество Николая Рубцова неотделимо от главных путей развития русской поэзии второй половины XX века, оно органично вписывается в национально-поэтическую традицию. В нем с особой силой отразились существенные черты и тенденции литературного процесса, обусловленные временем.
^ Секция математики
Подсекция «Алгебра и теория чисел»
Числа Каталана
Тимофеенко Игорь, 11 кл., МОУ СОШ № 92, школа
«Шаг в математику», МОУ ДОД ДТДиМ, г. Ростова-на-Дону.
Научный руководитель: ^ Кулабухов Сергей Юрьевич, кандидат
физико-математических наук, педагог дополнительного образования,
МОУ ДОД ДТДиМ г. Ростова-на-Дону.
Работа посвящена числам Каталана, одному из важных разделов комбинаторики. Числа Каталана не являются частью школьной программы, но, тем не менее, нам эта тема показалась очень интересной. В связи с этим я проанализировал много задач на эту тему, некоторые из которых решил сам. И заметил одну важную особенность всех задач, связанных с этой темой: решение их сводится к установлению однозадачного соответствия между данной задачей и любой другой, решённой до этого (обычно к задаче о расстановке скобок). В связи с этим были проанализированы подходы к решению данных задач. Так же была выведена нерекуррентная формула n-го члена, которая во многом облегчает решение и нахождение числового значения задачи.
^ Произведение квадратных трехчленов
Трофимов Михаил, 11 кл., МОУ ДОД ДДТ школа «Эрудит»,
г. Шахты, Ростовская область.
Руководитель: Карташян Марсел Вардгесович, педагог дополнительного образования, МОУ ДОД ДДТ школа «Эрудит»,
г. Шахты, Ростовская область.
В данной работе рассматривается произведение нескольких квадратных трехчленов. Была поставлена задача отыскания формулы, сходной с биномом Ньютона для квадратных трехчленов. Доклад начинается с комбинаторики: сочетания из элементов двух множеств.
После получения формулы числа сочетаний из элементов двух множеств, рассматривается произведение нескольких квадратных трехчленов. Сначала количество множителей равно двум, трем, четырем, а затем методом математической индукции доказывается общая формула (когда число квадратных трехчленов равно n). Далее, как частный случай, из этой формулы получается формула разложения квадратного трехчлена в степени n. Приводится сравнение между этой формулой и другой – биномом Ньютона. Получены свойства разложения по этой формуле. Интересны следствия из формулы и свойства трехчленных коэффициентов, вот основные из них:
Бином Ньютона является частным случаем полученной формулы.
При разложении всегда получается многочлен степени 2n с 2n+1 членами.
Все коэффициенты разложения либо имеют вид T
 =puqv, либо равны сумме чисел такого вида.
=puqv, либо равны сумме чисел такого вида.Известно, что сумма биноминальных коэффициентов равна 2n. Если подставить в формуле p=q=1, то получим сумму трехчленных коэффициентов, равную 3n, причем сумма коэффициентов на чётных местах равна
 , а на нечётных местах –
, а на нечётных местах – 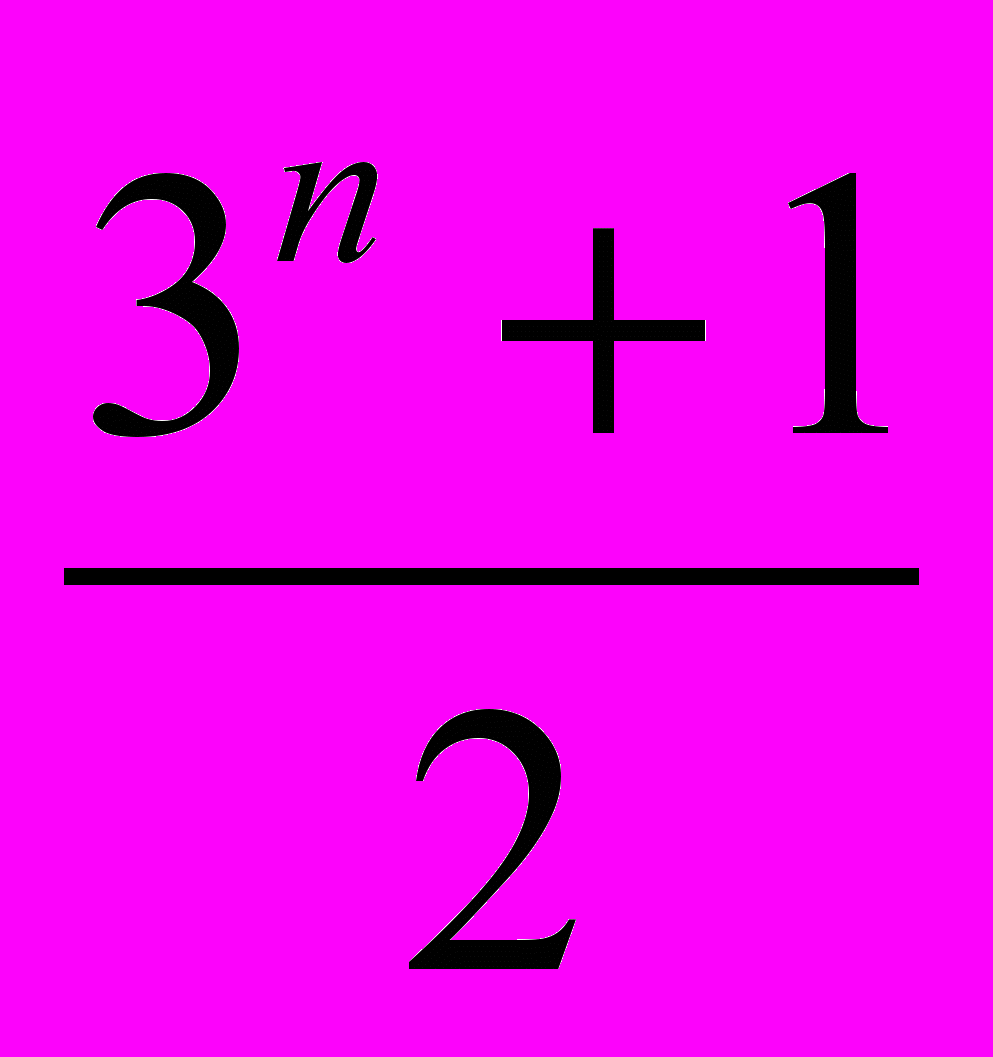 .
.Известно, что если через каждую цифру 1 левого столбца треугольника Паскаля провести прямую под 45о, то сумма чисел, которые получаются при пересечении этих прямых, является членом последовательности Фибоначчи: 1,1,2,3,5,8,13,…
Если поступить с трехчленными коэффициентами так же, как с треугольником Паскаля, то получается последовательность:
1,2,4,7,13,24,…
Каждый член этой последовательности, начиная с четвертого, получается суммированием трех последних.
В завершающей части доклада решаются задачи с применением этой формулы. Создана компьютерная программа, генерирующая таблицу трехчленных коэффициентов.
^ Признаки делимости в альтернативных позиционных системах счисления
Бессмертный Андрей, 9 кл., МОУ лицей № 11, г. Шахты,
Ростовская область.
Руководитель: ^ Росенко Олег Валерьевич, учитель математики,
МОУ лицей № 11, г. Шахты, Ростовская область.
Занимаясь в школе «Эрудит», мы сталкиваемся с различными олимпиадными задачами на использование признаков делимости. Интересны явилось и то, что признаки делимости имеют различную структуру для определенных классов делителей, а для некоторых делителей удобного в работе признака не существует. На уроках информатики мы знакомился с позиционными системами счисления, в основании которых – натуральное число, отличное от 10. Возникла идея обнаружения признаков делимости в позиционных системах счисления и возможного их использования для составления олимпиадных задач.
Исходя из этого, мы поставили следующие цели исследовательской работы: изучить признаки делимости в десятеричной системе счисления; найти универсальный метод нахождения признаков делимости; определить возможность его применения в альтернативных позиционных счислениях; выявить признаки делимости в конкретной системе счисления (восьмеричной, выбрана исходя из простоты проверки вычислений с использованием стандартного инженерного калькулятора); составить олимпиадные задачи на применение признаков делимости в альтернативных системах счисления.
По нашему мнению, исследовательская работа актуальна: для учащихся, интересующихся олимпиадной тематикой (приведены олимпиадные задачи с решением); для желающих узнать больше нового в теории чисел (подробно разобрано выявление признаков делимости в различных системах счисления); для всех желающих подняться на более высокий творческий уровень.
При решении поставленных задач использованы следующие методы: метод аналогий (перенесение «идей» признаков делимости 10-теричной системы счисления на другие позиционные системы счисления); метод перебора вариантов (проверены с помощью признака Паскаля формы признаков делимости на числа от 2 до n, где n – основание системы счисления, причем описаны только удобные для использования признаки делимости); конструирование (использовался при составлении задачи с новой тематикой: применение признаков делимости для определения основания системы).
К главным итогам работы можно отнести прежде всего то, что:
- выявлен универсальный метод обнаружения признаков делимости в различных позиционных системах счисления (Признак Паскаля);
- найдены признаки делимости в 8-меричной системе счисления, а также признаки делимости на n+1 и n-1, где n – основание системы счисления, а именно признаки делимости на: 2 (аналогичный признаку делимости на 2); на 4 (аналогичный признаку делимости на 5); на 3 и 9 (аналогичный признаку делимости на 11); на 7 (аналогичный признаку делимости на 9);
- использованы найденные признаки для составления задач, большинство из которых имеет олимпиадный уровень (ко многим задачам были приведены подробные решения; приведены также задачи на «счастливые» билеты; интересная задача-фокус на преобразования в 8-ричной и 10-ричной системах счисления с раскрытием его секрета; задача на определение неизвестной системы счисления).
^ Комплексные числа
Ковалёва Анастасия, 10 кл., МОУ СОШ № 6,
г. Сальск, Ростовская область.
Руководитель: Новикова Лина Николаевна, учитель математики,
МОУ СОШ № 6, г. Сальск, Ростовская область.
В программе математики школьного курса теория чисел вводится на примерах множеств натуральных чисел, целых, рациональных, иррациональных, т.е. на множестве действительных чисел, изображения которых заполняют всю числовую ось. Но уже в восьмом классе запаса действительных чисел не хватает - решая квадратные уравнения при отрицательном дискриминанте. Поэтому было необходимо пополнить запас действительных чисел при помощи комплексных чисел, для которых квадратный корень из отрицательного числа имеет смысл.
Цель: расширение знаний учащихся о числовых множествах, о решении широкого класса задач алгебраического содержания, о решении уравнений любой степени и о решении задач с параметрами.
В теоретической части работы приведены понятие комплексного числа, правила сложения, вычитания, умножения, деления, операция сопряжения для комплексных чисел в алгебраической форме, степень мнимой единицы, модуль комплексного числа, а также излагается правило извлечения квадратного корня из комплексного числа. В практической части представлены примеры выполнения действий с комплексными числами, решения уравнений, преобразования выражений.
Получены следующие результаты. Дано систематическое изложение методов решения задач с комплексными числами; рассмотрены действия над комплексными числами в тригонометрической форме, а также в алгебраической форме, приведены решения уравнений 2-й, 3-й и 4-й степеней; представлено разложение квадратных трехчленов на множители, упрощение выражений.
Материал может быть использован в учебном процессе в курсе алгебры в учебном заведении, в классах с углубленным изучением математики и на элективных курсах, а также при изучении математики во внеурочное время (в математическом кружке).
^ Нестандартная формула нахождения корней
квадратного уравнения, ее численный анализ
Назаренко Денис, 8 кл., МОУ СОШ № 31, г. Ростов-на-Дону.
Руководитель: ^ Кряквина Лилия Низамитдиновна, учитель математики,
МОУ СОШ № 31, г. Ростов-на-Дону.
Работа посвящена, казалось бы, хорошо известной и изученной теме «Корни квадратного уравнения». В ней предлагается к рассмотрению малоизвестная нестандартная формула нахождения корней квадратного уравнения. Следует отметить, что представленный в работе материал нетривиален и полезен для приложений. Кроме заимствованного вывода нестандартной формулы нахождения корней квадратного уравнения, в работе приводится более простое и понятное доказательство этой формулы.
Во второй части работы проводится численный анализ и сравнение двух формул вычисления корней. Особенно анализируется случай, когда старший коэффициент мал по абсолютной величине по сравнению с остальными коэффициентами. Этот случай важен, так как в стандартной формуле нахождения корней квадратного уравнения производится деление на маленькое число, что иногда приводит к существенному возрастанию погрешностей вычисления.
В работе численно исследуются частные случаи полученной формулы. Рассмотрены квадратные уравнения, в которых корни вычисляются с достаточно большой точностью. Затем, после внесения погрешностей при вычислениях, находятся корни квадратного уравнения по стандартной формуле и исследуемой формуле. Полученные значения сравниваются с уже найденными более точными значениями и между собой. Анализ абсолютных погрешностей показывает в некоторых случаях большую точность вычислений при использовании нестандартной формулы.
Отсюда можно сделать вывод о том, что эта формула позволяет уменьшать погрешность вычисления при некоторых значениях входящего в нее параметра. Поэтому несомненна ее практическая значимость. Но кроме преимущества при численных расчетах, связанного с необходимостью нахождения корней квадратного уравнения, использование в учебном процессе нестандартной формулы имеет и мировоззренческий характер. А именно, оно помогает в формировании нестандартных подходов к решению как хорошо известных, так и новых и оригинальных задач.
^ Подсекция общей математики
Вероятностный метод
Малясова Виктория, 10 кл., МАОУ лицей № 14 «Экономический»,
г. Ростов-на-Дону.
Руководитель: ^ Райгородский Андрей Михайлович, доктор физико-математических наук, профессор математической статистики и случайных процессов МГУ.
В математике часто бывает, что решить задачу из одной области помогают специалисты из другой.
Целью нашего исследования было выяснить, как в решении задач может помочь владение теорией вероятности. Нам предстояло найти задачи, в которых можно применить вероятностный метод.
Как оказалось, с помощью этого метода часто удаётся доказать существование объектов, построить которые в явном виде весьма и весьма затруднительно. В частности, в работе приведены доказательства двух теорем существования – одна из теории графов, другая из геометрии.
На наш взгляд, математику любой специализации полезно иметь вероятностный метод в своём арсенале средств для решения задач. Что и обуславливает актуальность этой работы.
^ Удача на ЕГЭ в формулах теории вероятностей
Таранин Руслан, 9 кл., МОУ лицей № 11, г. Шахты, Ростовская область.
Руководитель: Росенко Олег Валерьевич, учитель математики,
МОУ лицей № 11, г. Шахты, Ростовская область.
Для учеников 9-11 классов одно из наиважнейших событий сейчас – удачная сдача Единого Государственного Экзамена. Сколько раз мы слышали от своих наименее подготовленных к сдаче сверстников такие слова: «Ничего... На тройку угадаю…» И тут стоит всерьез задуматься - какова же действительно вероятность получения оценки «три» при постановке ответов наудачу. Это и стало темой нашего проекта.
Для раскрытия темы проекта поставлены такие цели и задачи:
Определить погрешность статистики ЕГЭ, то есть найти реальный процент учащихся, которые «претендовали» разве что на оценку «2», но благодаря собственной удаче получили «3»;
Раскрыть действительное представление школьников о вероятности угадывания заданий в тестах ЕГЭ. Установить, совпадает ли их представление с расчетными данными;
Провести социологический опрос среди школьников старших классов - о вероятности угадать ответы на 4 вопроса из 10-ти, при условии, что в каждом вопросе 4 варианта ответа (норматив на 3 балла по статистике ЕГЭ за 2009 год) и 6 вопросов из 16-ти (норматив на «3» балла по статистике ЕГЭ за 2004 год);
Нахождение вероятности правильного ответа наугад на 4 вопроса из 10-ти, а также на 6 из 16-ти с помощью формулы, найденной практическим путем, и формулы Бернулли;
Проведение среди учащихся старших классов тестов на «да» и «нет», подсчет вероятности проставления ответов наугад на оценку «3»;
Проведение тестов ЕГЭ среди школьников 9-х классов, подтверждение вычислений вероятности данными эксперимента.
Почему же эта тема актуальна? На некоторых сайтах вскользь упоминается вероятность угадывания вопросов на оценку «3» в тестах ЕГЭ, однако полных сведений по данному вопросу нигде не представлено. Наша работа восполнит пробелы в анализе результатов ЕГЭ, в статистической обработке результатов, в прогнозе результатов тестирования в другой форме.
Использованы такие методы, как: социологический опрос среди школьников 9-х классов, регрессионный анализ экспериментальных данных тестов, вероятностные расчеты, наблюдение и анализ экспериментов.
По завершении выполнения проекта можно отметить следующие результаты:
Вероятность угадать 4 ответа из 10-ти (порог на оценку «3» в 2009 году) приближенно равна 49%.
Вероятность угадать 6 из 16-ти вопросов (порог на оценку «3» в 2004 году) приближенно равна 57%.
В основном, участники социологического опроса имеют завышенную оценку вероятности угадывания 4-х из 10 ответов на вопросы. Относительные погрешности равны: |22.5 – 38.51|/22,5
 73% и |49 – 55.1|/49
73% и |49 – 55.1|/49  12%.
12%.Процент неуспевающих школьников в статистике ЕГЭ 2004 и 2009 года занижен. При реальных 7% (2009) он составляет 14%, исходя из данных, полученных в нашем проекте. При 19,5% (2004) он составляет 45,3%.
Паркеты
^ Колотнева Татьяна, 10 кл., МОУ СОШ № 1, х. Маяк, Сальский район.
Руководитель: Будко Любовь Фёдоровна, МОУ СОШ № 1,
х. Маяк, Сальский район, Ростовская область.
В современной жизни паркеты настолько часто встречаются, что мы их не замечаем. Они на обоях, на полу, на тротуарах. Привычный тетрадный лист в клеточку – пример паркета. Составить красивый необычный паркет – это, конечно, дело дизайнеров. Меня привлекает специальность дизайнера и красота паркетов.
На первом этапе своей работы я познакомилась с понятием паркета и изучила историю их возникновения.
Орнамент имеет свою историю. Его истоки уходят в те времена, когда человек перешел к оседлому образу жизни и начал изготавливать орудия труда и предметы быта. Всё разнообразие паркетов можно разделить на следующие виды: правильный паркет, полуправильный паркет, паркет из неправильных многоугольников, геометрический орнамент, растительный орнамент и другие.
Особенно внимательно я отнеслась к паркету на плоскости Лобачевского, так как составление паркета Лобачевского подчиняется математическим законам. Опираясь на эти законы, я составила таблицу возможно допустимых углов. Она в дальнейшем помогла мне решать практические задачи на составление паркетов.
Интерес вызвало у меня решение прикладных задач. В своей работе я привожу решение 12 задач. Считаю - задачи повышают интерес к математике и увеличивают ее прикладную направленность.
Материал работы можно использовать для профильных курсов в девятых классах, так как это может способствовать, например, выбору такой профессии, как дизайнер. Изучение этой темы поможет окончательно остановить свой выбор на профессии дизайнера и подстегнет к углубленному изучению курса математики. Ведь теория паркетов тесно связана с математическими формулами, теоремами, свойствами, расчётами.
