От лат cavitas пустота), образование в капельной жидкости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац
| Вид материала | Документы |
- Вывихи. Переломы, 241.71kb.
- От лат evaporo испаряю и греч grapho пишу), метод получения изображений объектов, 2696.94kb.
- Реферат от лат rеfеrо "сообщаю", 198.27kb.
- Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
- Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
- Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
- Реферат от лат. «сообщать», 61.18kb.
- Лекция. Взаимосвязанные рынки, 285.49kb.
- Реферат Реферат, 36.91kb.
- Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.
281
ляется к.-л. тремя координатами, напр. прямоугольными декартовыми х, у, z, а закон движения задаётся тремя ур-ниями: x=f1(t), y=f2(t), z=f3(t). Исключив из этих ур-ний время t, можно найти траекторию точки. Естественный (или траекториый) способ применяется обычно, когда известна траектория точки по отношению к выбранной системе отсчёта. Положение точки определяется расстоянием s=О1М от выбранного на траектории начала отсчёта O1, измеренным вдоль траектории и взятым с соответствующим знаком (рис. 1), а закон движения даётся ур-нием s=f(t), выражающим зависимость s от времени t. Зависимость s от t может быть также задана графиком движения, на к-ром в выбранном масштабе вдоль оси t отложено время, а вдоль s — расстояние (рис. 2), или
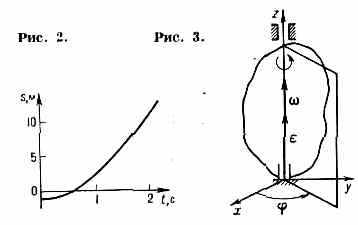
таблицей, где в одном столбце даются значения t, а в другом — соответствующие им значения s. Осн. кинематич. хар-ками движущейся точки явл. её скорость и ускорение.
Способы задания движения тв. тела зависят от вида его движения, а число ур-ний движения — от числа степеней свободы тела (см. Степеней свободы число). Простейшими явл. поступательное движение и вращательное движение тв. тела. При поступат. движении все точки тела движутся одинаково, и его движение задаётся и изучается так же, как движение одной точки. При вращат. движении вокруг неподвижной оси АВ (рис. 3) тело имеет одну степень свободы; его положение определяется углом поворота , а закон движения задаётся ур-нием: =f(t). Осн. кинематич. хар-ками явл. угловая скорость и угловое ускорение тела. Зная и , можно определить скорость и ускорение любой точки тела.
Более сложным явл. движение тела, имеющего одну неподвижную точку и обладающего тремя степенями свободы (напр., гироскоп). В этом случае положение тела относительно системы отсчёта определяется к.-н. тремя углами (напр., Эйлеровыми углами), а закон движения — ур-ниями, выражающими зависимость этих углов от времени. Осн. кинематич. хар-ками явл. и тела. Движение тела
слагается из серии элем. поворотов вокруг непрерывно меняющих своё направление мгновенных осей вращения ОР, проходящих через неподвижную точку О (рис. 4).
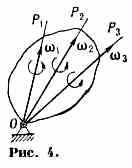
Самый общий случай — движение свободного тв. тела, имеющего шесть степеней свободы. Положение тела определяется тремя координатами одной из его точек, наз. полюсом (в задачах динамики за полюс принимается обычно центр тяжести тела), и тремя углами, к-рые выбираются так же, как для тела с неподвижной точкой. Закон движения тела задаётся шестью ур-ниями, выражающими зависимости названных координат и углов от времени. Движение тела слагается из поступательного вместе с полюсом и вращательного вокруг этого полюса, как вокруг неподвижной точки. Такими, напр., являются: движение в воздухе артиллерийского снаряда или самолёта, совершающего фигуры высш. пилотажа, движения небесных тел. Осн. кинематич. хар-ки — скорость и ускорение поступат. части движения, равные скорости и ускорению полюса, и угл. скорость и угл. ускорение вращения тела вокруг полюса. Все названные хар-ки (как и кинематич. хар-ки для тела с неподвижной точкой) определяются по ур-ниям движения; зная эти хар-ки, можно вычислить скорость и ускорение любой точки тела. Частным случаем рассмотренного движения явл. плосконаправленное (или плоское) движение тв. тела, при к-ром все его точки движутся параллельно нек-рой плоскости. Подобное движение совершают звенья многих механизмов и машин.
В К. изучают также сложное движение точек или тел, т. е. движение, рассматриваемое одновременно по отношению к двум (или более) взаимно перемещающимся системам отсчёта. При этом одну из систем отсчёта рассматривают как основную (её условно наз. неподвижной), а перемещающуюся по отношению к ней систему отсчёта наз. подвижной; в общем случае подвижных систем отсчёта может быть несколько. При изучении сложного движения точки её движение, а также скорость и ускорение по отношению к осн. системе отсчёта наз. условно абсолютными, а по отношению к подвижной системе — относительными. Движение самой подвижной системы отсчёта и всех неизменно связанных с нею точек np-ва по отношению к осн. системе наз. п е р е н о с н ы м движением. Осн. задачи К. сложного движения заключаются в установлении зависимостей между кинематич. хар-ками абс. и относит. движений точки (или тела) и хар-ками движения подвижной системы отсчёта, т. е. переносного движения (см. Относительное движение).
Для тв. тела, когда все составные (т. е. относительные и переносные) движения явл. поступательными, абс. движение также поступательное со скоростью, равной геом. сумме скоростей составных движений. Если составные движения тела явл. вращательными вокруг осей, пересекающихся в одной точке (как, напр., у гироскопа), то результирующее движение также явл. вращательным вокруг этой точки с угл. скоростью, равной геом. сумме угл. скоростей составных движений. Если же составными движениями тела явл. и поступательные и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
В К. сплошной среды устанавливаются способы задания движения этой среды, рассматривается общая теория деформаций и определяются т. н. ур-ния неразрывности (сплошности) среды (подробнее см. Гидромеханика, Упругости теория). • См. лит. при ст. Механика.
С. М. Тарг.
КИНЕМАТИЧЕСКАЯ ВЯЗКОСТЬ (кинематический коэффициент вязкости), см. Вязкость. КИНЕТИКА (от греч. kinetikos -приводящий в движение), раздел механики, в к-ром исследуется механич. состояние тела в связи с физ. причинами, его определяющими. К. разделяется на динамику — учение о движении тел под действием сил и статику — учение о равновесии тел.
КИНЕТИКА ФИЗИЧЕСКАЯ, микроскопич. теория процессов в статистически неравновесных системах. Она изучает методами квант. или классич. статистической физики процессы переноса энергии, импульса и в-ва в разл. физ. системах (газах, плазме, жидкостях, тв. телах), а также влияние на эти системы внеш. полей.
В отличие от термодинамики неравновесных процессов и электродинамики сплошных сред, К. ф. исходит из представления о мол. строении рассматриваемых сред и силах вз-ствия между их ч-цами, что позволяет вычислить кинетические коэффициенты, диэлектрич. и магн. проницаемости и др. подобные хар-ки сплошных сред.
К. ф. включает кинетическую теорию газов из нейтр. атомов или молекул, статистич. теорию неравновесных процессов в плазме, теорию явлений переноса в тв. телах (диэлектриках, металлах и ПП), кинетику магн. процессов и теорию кинетич. явлений, связанных с прохождением быстрых ч-ц через в-во. К ней же относится теория процессов переноса в квантовых жидкостях и кинетика фазовых переходов.
В К. ф. используют существ. различие времён релаксации в неравновесных процессах. Напр., для газа из ч-ц или квазичастиц время свободного пробега между столкновениями значительно больше времени столкновения t. На временных ин-
282
тервалах, значительно превышающих t, в системе происходит усреднение хаотич. движений ч-ц («хаотизация», или «перемешивание», газа). Это даёт возможность перейти от описания неравновесного состояния ф-цией распределения ч-ц по всем координатам q и импульсам р к упрощённому описанию на основе одночастичной ф-ции распределения одной ч-цы по её координатам и импульсам (в этом случае можно считать, что все ч-цы ведут себя одинаково).
Осн. метод К. ф.— построение и решение кинетического уравнения Больцмана для ф-ции распределения молекул f(q, p, t) в их фазовом пространстве (q, p). Произведение fdqdp есть ср. вероятное число молекул в элементе фазового объёма dqdp(dq= dx dy dz, dp=dpxdpydpz). Любой рассматриваемый неравновесный процесс связан с перераспределением молекул (атомов) в элементах фазового объёма за счёт их свободного движения или в результате столкновений. Ф-ция распределения f удовлетворяет кинетич. ур-нию Больцмана, учитывающему все возможные причины перераспределения молекул:
df/dt+v•gradf+pдf/дp=Stf,
где v — скорость молекул; v•gradf — изменение числа молекул в элементе фазового объёма, связанное с их движением; р•(дf/дp) — изменение числа молекул, вызванное действием внеш. сил; Stf — интеграл столкновений, определяющий разность числа молекул, приходящих в элемент объёма и убывающих из него вследствие столкновений.
Для газа из одноатомных молекул или более сложных молекул, но без учёта их внутр. степеней свободы
Stf=∫w(f'f'1-ff1)dp1dp'dp'1,
где w — вероятность столкновения, связанная с дифференциальным эфф.
сечением d=(w/(v-v1))dp'dp'1, p, р1—
импульсы молекул до столкновения,
р', p'1 — их импульсы после столкновения, f, f1 — ф-ции распределения молекул до столкновения, f', f'1 — их ф-ции распределения после столкновения. В простейшем приближении Stf=-(f-f0)/, где f0 — равновесная ф-ция распределения, — ср. время релаксации.
Для газа из сложных молекул, обладающих внутр. степенями свободы, напр. двухатомных молекул с собств. моментом вращения М, ф-ция распределения зависит также от М и нужно учесть увеличение фазового объёма молекулы, связанное с её вращением.
К. ф. позволяет получить ур-ния баланса ср. плотностей массы, импульса и энергии. Напр., для газа плотность , гидродинамич. скорость
v и ср. энергия ξ удовлетворяют ур-ниям баланса:
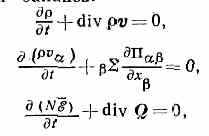
где П=∫mvvfdp — тензор плотности потока импульса, Q= ∫ξvfdp —
плотность потока энергии, N — число ч-ц.
Если состояние газа мало отличается от равновесного, то в малых элементах объёма устанавливается локально-равновесное распределение, характеризуемое Максвелла распределением с темп-рой, плотностью и гидродинамич. скоростью, соответствующими рассматриваемому элементу объёма. В этом случае неравновесная ф-ция распределения мало отличается от локально-равновесной и решение кинетич. ур-ния даёт малую к ней поправку, пропорц. градиентам темп-ры grad Т и гидродинамич. скорости gradv. Неравновесный поток импульса даёт сдвиговую вязкость, а для газов с внутр. степенями свободы он содержит ещё член, пропорц. div v, к-рый приводит к объёмной вязкости. Плотность потока энергии Q пропорц. grad Т (обычная теплопроводность), а в случае смеси газов выражение для Q содержит ещё член, пропорц. градиенту концентрации gradс (Дюфура эффект). Поток в-ва в смеси газов содержит член, пропорц. градиенту концентрации (обычная диффузия), и член, пропорц. градиенту темп-ры (термодиффузия). Подобные соотношения наз. линейными соотношениями между термодинамич. силами и потоками. Для входящих в них коэфф. (напр., сдвиговой вязкости и объёмной вязкости, коэфф. теплопроводности, диффузии, термодиффузии, эффекта Дюфура) К. ф. даёт выражения через эфф. сечения столкновений, следовательно через константы межмол. вз-ствия. Кинетич. коэфф. для перекрёстных явлений, напр. для термодиффузии и для эффекта Дюфура, оказываются равными (частный случай общих соотношений взаимности Онсагера; см. Онсагера теорема).
Ур-ния баланса импульса, энергии, числа ч-ц определ. сорта вместе с линейными соотношениями между термодинамич. силами и потоками позволяют получить Навье — Стокса уравнения, теплопроводности уравнение, ур-ние диффузии. Такой гидродинамич. подход к решению задач о переносе физ. величин справедлив, если длина свободного пробега l значительно меньше характерных размеров областей неоднородности.
К. ф. позволяет исследовать явления переноса в разреженных газах и в том случае, когда отношение длины свободного пробега l к характерным
размерам L системы (т. е. число Кнудсена l/L) уже не очень мало и имеет смысл рассматривать поправки порядка l/L (слабо разреженные газы). В этом случае ур-ния К. ф. позволяют объяснить явление температурного скачка на границе потока газа и тв. поверхности, а также скольжение потока в слое порядка l вблизи поверхности.
Для сильно разреженных газов, когда l/L>>1, гидродинамич. ур-ния неприменимы и необходимо решать кинетич. ур-ние с определёнными граничными условиями на поверхностях. Эти условия определяются ф-цией распределения молекул, рассеянных из-за вз-ствия со стенкой. Рассеянный поток может приходить в тепловое равновесие со стенкой (полная аккомодация), но в реальных случаях это не достигается. Для сильно разреженных газов роль коэфф. теплопроводности играют коэфф. теплопередачи. Напр., кол-во теплоты q, переносимое через ед. площади параллельных пластинок, между к-рыми находится разреженный газ, равно: q=(T2- T1)/L, где t1 и T2 — темп-ры пластинок, L — расстояние между ними, — коэфф. теплопередачи.
Для описания процессов в плазме К. ф. пользуется двумя ф-циями распределения — эл-нов fe и ионов fi, удовлетворяющих системе двух кинетич. ур-ний. На ч-цы плазмы действуют силы F=Ze(E+1/c[vB]), где
Ze — заряд ч-цы, Е — напряжённость электрич. поля, В— индукция магн. поля, удовлетворяющие Максвелла уравнениям. В ур-ния Максвелла входят ср. значения плотностей токов и зарядов. Их определяют при помощи ф-ций распределения fe и fi. Т. о., кинетич. ур-ния и ур-ния Максвелла представляют собой связанные системы ур-ний, описывающие все явления в плазме.
К. ф. неравновесных процессов в диэлектриках основана на решении кинетич. ур-ния Больцмана для фононов крист. решётки (ур-ние Пайерлса). В частности, кинетич. ур-ние для фононов позволяет исследовать теплопроводность и поглощение звука в диэлектриках.
К.ф. металлов основана на решении кинетич. ур-ния для эл-нов с учётом их вз-ствия с фононами. Рассеяние эл-нов на фононах обусловливает появление электрич. сопротивления. К. ф. теоретически объясняет гальваномагнитные, термоэлектрич. и термомагн. явления, скин-эффект и циклотронный резонанс в ВЧ полях и ряд др. эффектов в металлах. Для сверхпроводников она объясняет особенности их ВЧ поведения.
К. ф. магнитных явлений основана на решении кинетич. ур-ния
283
для магнонов, что позволяет вычислить магн. восприимчивость систем в перем. полях, изучить кинетику процессов намагничивания.
К. ф. неравновесных процессов в жидкостях требует более общего подхода, т. к. в этом случае одно-частичная ф-ция распределения не раскрывает специфики явлений и необходимо рассматривать двухчастичную ф-цию распределения. Однако для жидкости возможен гидродинамич. подход, т. к. для неё существуют медленно меняющиеся гидродинамич. переменные — плотность числа ч-ц, плотность энергии, плотность импульса. В течение малого времени релаксации в макроскопически малых объёмах жидкости устанавливается локально-равновесное распределение, подобное равновесному распределению Гиббса, но с темп-рой, хим. потенциалом и гидродинамич. скоростью, к-рые соответствуют рассматриваемому малому объёму жидкости. Для достаточно медленных процессов и когда масштабы пространств. неоднородности значительно меньше масштаба корреляции между ч-цами жидкости, неравновесная ф-ция распределения близка к локально-равновесной и можно найти к ней поправку, пропорц. градиентам темп-ры, гидродинамич. скорости и хим. потенциалам компонентов. Полученная равновесная ф-ция распределения позволяет вычислить потоки импульса, энергии и в-ва и вывести ур-ния Навье — Стокса, теплопроводности и диффузии. Кинетич. коэфф. оказываются в этом случае пропорц. пространственно-временным корреляц. ф-циям потоков энергии, импульса и в-ва данного сорта (ф-лы Грина— Кубо).
• Лифшиц Е. М., Питаевский Л. П., Физическая кинетика, М., 1979 (Теоретическая физика, т. 10); Гуров К. П., Основания кинетической теории. Метод Н. Н. Боголюбова, М., 1968; Климонтович Ю. Л., Кинетическая теория неидеального газа и неидеальной плазмы, М., 1975; Ч е п м е н С., К а у л и н Т., Математическая теория неоднородных газов, пер. с англ., М., 1960; Ф е р ц и г е р Дж., К а п е р Г., Математическая теория процессов переноса в газах, пер. с англ., М., 1976; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971;Балеску Р., Равновесная и неравновесная статистическая механика, пер. с англ., т. 2, М., 1978.
Д. Н. Зубарев.
КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ, раздел теор. физики, исследующий св-ва газов статистич. методами на основе представления об их мол, строении и определ. законе вз-ствия между молекулами. Обычно к К. т. г. относят лишь теорию неравновесных св-в газов, теория же их равновесных св-в — область статистической физики равновесных систем. Осн. объекты применения К. т. г.— газы, газовые смеси и плазма, однако теория последней выделилась в самостоят. область теор. физики.
Молекулы в газах движутся почти свободно в промежутках между столкновениями, приводящими к резкому изменению их скоростей. Время столкновения значительно меньше ср. времени свободного пробега молекул газа между столкновениями, поэтому теория неравновесных процессов в газах значительно проще, чем в жидкостях или тв. телах. Наблюдаемые физ. хар-ки газа представляют собой результат действия всех его молекул. Для вычисления этих хар-к нужно знать распределение молекул газа по скоростям и пр-ву, занятому газом, т. е. знать функцию распределения f(v, r, t). Произведение f(v,r,t)dvdr определяет вероятное число молекул, находящихся в момент времени t в элементе объёма dr=dxdydz около точки r и обладающих скоростями в пределах dv=dvxdvydvz вблизи значения v. Плотность n числа ч-ц газа в точке r в момент t равна: n(r, t)=∫f(v,r,t)dv. Осн. задача К. т. г.—
определение явного вида ф-ции f(v, r, t), поскольку она позволяет вычислить ср. значения величин, характеризующих состояние газа, и процессы переноса энергии, импульса и числа ч-ц, к-рые могут в нём происходить. Напр., v (r, t)=1/n∫│v│f(v, r, t)dv — средняя (по абс. величине) скорость молекул газа, a v2= 1/n∫v2f(v, r, t)dv — ср. квадрат их скорости.
Для идеального однородного газа в состоянии статистич. равновесия ф-ция f представляет собой Максвелла
распределение:
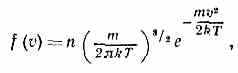
где т — масса молекулы. В этом случае
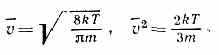
Передача энергии и импульса в газе происходит гл. обр. благодаря парным столкновениям молекул. Вероятное число парных столкновений молекул dv в ед. времени, находящихся в объёме dr и имеющих скорости в пределах dv1 и dv2 около значений скоростей v1 и v2, равно: dv=f(v1, r, t)Xf(v2, r, t)│v1-v2│ddv1dv2, где d — дифференциальное эфф. сечение сталкивающихся молекул в лаб. системе координат (так, =d2cos для модели молекул в виде упругих сфер с диаметром d, где — угол между относит. скоростью v1-v2 и линией центров сталкивающихся молекул, т. е. линией, соединяющей центры молекул в момент их наибольшего сближения). Это выражение для числа столкновений основано на «гипотезе мол. хаоса», т. е. на предположении об отсутствии корреляции между скоростями сталкивающихся молекул, что
справедливо для разреженных газов и газов ср. плотности.
Ср. длину свободного пробега молекул I можно определить через ср. число столкновений в ед. времени; l — ср. расстояние, к-рое прошла бы молекула за ср. время между столкновениями, двигаясь со ср. скоростью v, т. е. l=v/, где =1/n∫dv. Можно
также определить l как ср. расстояние между двумя последоват. столкновениями. В этом случае сначала вычисляют пробег для молекул с данной скоростью, а затем его усредняют по всем скоростям молекул. Для газа с молекулами в виде упругих сфер по первому определению l=1/2d2n, а по второму определению l=0,667/d2n , различие между ними
невелико.
Элем. теория явлений переноса основана на понятии ср. длины свободного пробега. Рассматривая перенос импульса, энергии, массы компонентов через единичную площадку в газе, можно соответственно получить значения коэфф. вязкости , теплопроводности и взаимной диффузии D12 двух компонентов (1 и 2) газовой смеси:
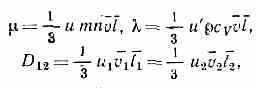
где с у — теплоёмкость при пост. объёме, =mn — плотность газа, u, u', u2 — численные коэффициенты порядка единицы, для вычисления к-рых нужна более точная теория.
Последовательная К. т. г. основана
