От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание А. В. Ефремов. Кварцевые часы Времени измерение, Кван­товые стандарты частоты. Кельвина уравнение Кельвина шкала Кеплера законы 2-й закон 3-й закон Орбита планеты — эллипс: F Керра постоянная Керра эффект Керра ячейка В. А. Замков. Килограмм на кубический метр Килограмм-метр в секунду

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КВАНТОМЕТР, многоканальная фотоэлектрич. установка для пром. спектрального анализа. См. также Спектральные приборы, Спектральная аппаратура рентгеновская.

КВАРКИ, гипотетич. материальные объекты, из к-рых, по совр. представ­лениям, состоят все адроны. Гипотеза о К. была высказана в 1964 М. Гелл-Маном и Г. Цвейгом (США) для объяс­нения закономерностей в спектроско­пии и св-вах адронов. Она возникла в связи с обнаружением большого числа резонансов и их успешной сис­тематизацией. Согласно кварковой ги­потезе, барионы состоят из трёх К. (антибарионы — из трёх антиквар­ков), мезоны — из К. и антикварка. Все известные в то время адроны можно было построить из К. трёх типов: u, d и s, обладающих спи­ном ¹/₂, барионным зарядом ¹/₃ и электрич. зарядами соотв. ²/₃, -¹/₃ и -¹/₃ элем. заряда е. В состав стран­ных частиц входит s-K.— носитель странности. В дальнейшем оказалось необходимым расширение семейства К. Были введены «очарованный» с-К. и «красивый» b-K. и предсказано су­ществование новых семейств адронов, часть из к-рых уже обнаружена (см. Мезоны со скрытым «очарованием», «Очарованные» частицы, Ипсилон-час­тицы). Возможно существование и др. типов К., в частности t-K.

Нек-рые барионы (напр., ⁺⁺ , ) оказываются состоящими из трёх оди­наковых К. в одном и том же состоя­нии, что запрещено принципом Пау­ли. Поэтому каждому типу («аро­мату») К. была приписана дополнит. внутр. хар-ка — квант. число «цвет», к-рое может принимать три значения. При этом барионам соответствует «бес­цветная» (т. е. антисимметричная по «цветам») комбинация трёх К., а ме­зонам — «бесцветная» сумма комби­наций К. и антикварка одинаковых «цветовых» индексов.

Гипотеза кварковой структуры ад­ронов оказалась в дальнейшем необ­ходимой для понимания динамики разл. процессов с участием адронов (глубоко неупругого рассеяния лепто­нов, образования адронных струй в е⁺е^--аннигиляции и в адрон-адронных процессах с большой передачей импульса и др.). Так, глубоко не­упругое рассеяние лептонов на адронах, согласно совр. представлениям, идёт с выбиванием К. лептоном и пре­вращением его и адронного остатка в струи адронов. Измерения хар-к таких струй (угл. распределения, ср. электрич. и ср. барионного зарядов в др.) даёт возможность судить о сред-

них (по «цветам») значениях квант. чисел К.— спине, электрич. и барионном зарядах и др.

Существуют более сложные вариан­ты кварковых теорий с целочисл. зарядами К., к-рые пока трудно экспериментально отличить от тео­рий с дробными зарядами.

Хотя гипотеза К. необходима для объяснения систематики и динамики адронов, К. в свободном состоянии не были обнаружены (несмотря на многочисл. их поиски на ускорителях высо­ких энергий, в косм. лучах и окру­жающей среде). Это даёт основание считать, что здесь физики встрети­лись с принципиально новым явле­нием природы — т. н. удержанием К. (точнее, удержанием «цвета»).

В квантовополевой теории К.— квантовой хромодинамике, к-рая стро­ится на основе локальной «цветовой» калибровочной симметрии, вз-ствие К. осуществляется посредством обмена «цветными» глюонами — безмассовы­ми ч-цами со спином 1. Характерной особенностью этой теории явл. убыва­ние «цветового» эффективного заряда К. и глюонов с уменьшением расстоя­ния, благодаря чему на малых расстоя­ниях К. ведут себя как квазисвобод­ные частицы. Считается, что рост «цветового» заряда с увеличением расстояния между К. приводит к рож­дению из вакуума пар К.-антикварк, к-рые «обесцвечивают» разделяемые К., превращая их в «бесцветные» адро­ны. Однако эту картину удержания «цвета» нельзя считать доказанной.

• Коккедэ Я., Теория кварков, пер. [с англ.], М., 1971; Л а н д с б е р г Л. Г., Поиски кварков, «УФН», 1973, т. 109, в. 4, с. 695; Г л э ш о у Ш., Кварки с цветом и ароматом, там же, 1976, т. 119, в. 4, с. 715; Н а м б у Й., Почему нет свободных квар­ков, там же, 1978, т. 124, в. 1, с. 147; Окунь Л. Б., Лептоны и кварки, М., 1981.

А. В. Ефремов.

КВАРЦ (нем. Quarz), природный и синтетич. монокристалл SiO₂ (наиб. распространённое на Земле соедине­ние). Существует четыре полиморфные модификации К., из к-рых приме­няется гл. обр. низкотемпературный -К. При нагревании выше 575°С -К., имеющий точечную группу сим­метрии 32, без разрушения приобре­тает структуру высокотемпературного К. с точечной группой симметрии 62. Плотность 2,65 г/см³, T_пл1470 °С, твёрдость по шкале Мооса 7. К. хи­мически стоек, оптически анизотро­пен, прозрачен для УФ и частично ИК излучения. К.— пьезоэлектрик, обла­дает нелинейными оптич. и электро-оптич. св-вами. Прозрачные разно­видности К.: горный хрусталь, аметист (фиолетовый), раухтопаз (дымчатый), морион (чёрный), цитрин (жёлтый). Монокристаллы К. применяются для изготовления пьезоэлектрич. преоб­разователей, фильтров, УЗ линий задержки, призм для спектрографов, монохроматоров, линз для УФ оп­тики и др.

Я. В. Переломова.

КВАРЦЕВЫЕ ЧАСЫ, прибор для точного измерения времени, ход которых определяется колебаниями квар­цевого генератора. Точность отсчёта времени обусловлена постоянством (стабильностью) частоты колебаний кварцевого резонатора (см. Пьезо­электричество) и его добротностью. Т. к. частота  прецезионного квар­цевого резонатора всё же зависит от темп-ры (/10^-8 на 1°С), то его помещают в термостат, в к-ром под­держивается пост. темп-pa с точ­ностью до 0,001°С. Помимо кварце­вого генератора, К. ч. содержат пре­образователи частоты колебаний (де­лители и умножители частоты), син­хронный двигатель, приводящий в движение стрелочные часы (или уст­ройство цифрового отсчёта), и кон­тактное устройство для подачи сиг­налов точного времени. К. ч. обычно снабжены устройством, выдающим на­бор стандартных частот для измерит. целей.

В бытовых К. ч. колебания миниа­тюрного кварцевого резонатора под­держиваются микросхемой, выраба­тывающей также сигналы, управляю­щие устройством цифрового отсчёта. Питание осуществляется малогабарит­ными батареями, циферблат обычно выполнен на основе жидких кристал­лов. Нек-рые модели наручных К. ч. могут работать в режиме секундомера или будильника и снабжаются кален­дарём.

• См. лит. при ст. Времени измерение, Кван­товые стандарты частоты.

М. Е. Жаботинский.

KDP, см. Дигидрофосфат. калия.

КЕЛЬВИН (К), единица СИ термодинамич. темп-ры, равная 1/273,16 части термодинамич. темп-ры тройной точ­ки воды. Названа в честь англ. фи­зика У. Томсона (лорда Кельвина, W. Thomson, Lord Kelvin). До 1968 именовалась градус Кельвина (°К). Применяется как ед. Междунар. практич. температурной шкалы, 1 К=1°С.

КЕЛЬВИНА УРАВНЕНИЕ, характе­ризует изменение давления пара жид­кости или растворимости тв. тел, вызванное искривлением поверхности раздела смежных фаз (жидкость — пар, тв. тело — жидкость). Так, над сферич. каплями жидкости давление насыщ. пара р повышено по сравне­нию с давлением насыщ. пара р₀ над плоской поверхностью при той же темп-ре Т, а над вогнутыми соотв. понижено. Растворимость с тв. в-ва с выпуклой поверхностью выше (с вог­нутой — ниже), чем растворимость с₀ плоских поверхностей того же в-ва. К. у. получено У. Томсоном в 1871 из условия равенства химических по­тенциалов в смежных фазах, находя­щихся в состоянии термодинамич. рав­новесия, и имеет вид:

p/p₀=c/c₀=exp(2v/rRT), где r — радиус ср. кривизны поверх­ности раздела фаз,  — межфазное

279


поверхностное натяжение, v — моляр­ный объём жидкости или тв. тела, R — универсальная газовая постоян­ная.

Т. к. значения р и с различны для ч-ц разных размеров или для участ­ков поверхностей, имеющих впадины и выступы, К. у. определяет направ­ление переноса в-ва (от больших значений р и с к меньшим) в процессе перехода системы к состоянию термодинамич. равновесия. Это приводит, в частности, к тому, что крупные капли или ч-цы растут за счёт испа­рения (растворения) более мелких, а неровные поверхности сглаживаются за счёт растворения выступов и за­полнения впадин. Заметные отличия р и с имеют место лишь при доста­точно малых r. Поэтому К. у. наибо­лее широко используется для хар-ки состояния малых объектов (ч-ц кол­лоидных систем, зародышей новой фазы) и при изучении капиллярных явлений.

КЕЛЬВИНА ШКАЛА, часто приме­няемое наименование термодинамич. температурной шкалы. Названа в честь У. Томсона, впервые (1848) предложившего принцип построения температурной шкалы на основе вто­рого начала термодинамики.

КЕПЛЕРА ЗАКОНЫ, три закона дви­жения планет, открытые нем. астро­номом И. Кеплером (J. Kepler) в нач. 17 в. Ниже приведены их совр. фор­мулировки.

1-й закон: при невозмущённом дви­жении (в двух тел задаче) орбита дви­жущейся матер. точки (планеты) есть кривая второго порядка, в одном из фокусов к-рой находится центр силы притяжения (Солнце). Т. о., орбита матер. точки в невозмущённом дви­жении — это одно из конич. сечений, т. е. окружность, эллипс (для пла­нет), парабола или гипербола.

2-й закон: при невозмущённом дви­жении площадь, описываемая радиу­сом-вектором движущейся точки, из­меняется пропорц. времени (рис.). Часто 2-й закон формулируют как закон площадей: радиус-вектор пла­неты в равные промежутки времени описывает равные площади.

3-й закон: при невозмущённом эллнптич. движении двух матер. точек (планет) вокруг центр. тела (Солнца) произведения квадратов времён об­ращения на суммы масс центральной и движущейся точек относятся как кубы больших полуосей их орбит, т. е.



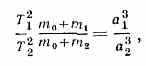
где t₁ и T₂ — периоды обращения двух точек, m₁ и m₂ — их массы, m₀ — масса центр. точки (Солнца), a₁ и а₂ — большие полуоси орбит точек (планет). Пренебрегая массами планет m₁ и m₂ по сравнению с мае-

сой Солнца m_солн, получаем 3-й К. з. в его первонач. форме: квадраты периодов обращений двух планет вок­руг Солнца относятся как кубы боль­ших полуосей их эллиптич. орбит. 3-й К. з. в применении к планетам, спутникам планет, компонентам двой­ных звёзд позволяет подсчитать массы планет, сумму масс двойной звёздной системы (если известны период обращения компонент и параллакс сис­темы), расстояния до двойных сис­тем (т. н. динамич. параллаксы).



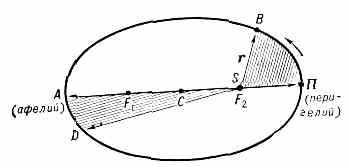
Орбита планеты — эллипс: F₁ и F₂ — фокусы эллипса, в одном из к-рых находится Солнце S; СП=СА — большая полуось орбиты; r — радиус-вектор планеты; отрезки траек­тории ПВ и AD планета проходит за одина­ковое время; площади секторов SПB=SAD.


К. з., найденные из наблюдений, были вы­ведены Ньютоном как строгое реше­ние задачи двух тел. Однако в дейст­вительности, в результате взаимного влияния планет Солнечной системы, траектории планет — сложные про­странств. кривые, к-рые можно ин­терпретировать как эллиптические лишь за время одного-двух оборотов.

• Дубошин Г. Н., Небесная механика. Основные задачи и методы, 2 изд., М., 1968; Гребеников Е. А., Рябов Ю. А., Поиски и открытия планет, М., 1975.

КЕРМА (сокр. англ. kinetic energy released in matter — кинетич. энер­гия, освобождённая в в-ве), сумма начальных кинетич. энергий всех заряж. ч-ц, образуемых нейтронами, рентгеновскими и -квантами в ед. массы облучаемого в-ва в результате вз-ствия с в-вом. К. измеряется в грэях (СИ) или в радах. К.— мера энер­гии, переданной излучением заряж. ч-цам в данной точке облучаемого объёма. Т. к. ч-цы теряют энергию на длине пробега, то пространств. распределение поглощённой дозы в в-ве отличается от распределения К., и тем больше, чем больше пробеги ч-ц. Приращение К. в ед. времени наз. мощностью К.

• См. лит. при ст. Дозиметрия.

Г. Б. Радзиевский.

КЕРРА ПОСТОЯННАЯ, константа пропорциональности, связывающая от­носит. величину индуцированного электрич. полем двупреломления изот­ропной центросимметричной среды с квадратом напряжённости электрич. поля (см. Керра эффект). К. п. харак­теризует электрооптич. св-ва среды.

КЕРРА ЭФФЕКТ, квадратичный электрооптич. эффект, возникновение двойного лучепреломления в оптически изотропных в-вах (жидкостях, стёк­лах, кристаллах с центром симмет­рии) под воздействием однородного электрич. поля. Открыт шотл. физиком Дж. Керром (J. Kerr) в 1875. Помещённое в электрич. поле изотроп­ное в-во становится анизотропным, приобретая св-ва одноосного кристал­ла (см. Кристаллооптика), оптич. ось к-рого направлена вдоль поля. Возможная схема наблюдения К. э. изображена на рисунке. Между скре­щёнными поляризатором П и анализа­тором А находится ячейка Керра



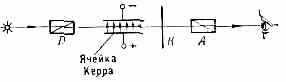
Схема установки для наблюдения эффекта Керра.

(плоский конденсатор, заполненный прозрачным изотропным в-вом). В от­сутствии электрич. поля свет преоб­разуется в линейно поляризованный в призме П и полностью гасится приз­мой А, не проходя к наблюдателю. При наложении электрич. поля ли­нейно поляризованная световая волна в в-ве распадается на две, поляризо­ванные вдоль поля (необыкновенная волна) и перпендикулярно полю (обык­новенная волна). Эти волны имеют в в-ве разл. скорости распростране­ния, вследствие чего выходящий из среды свет оказывается эллиптически поляризованным и частично проходит через анализатор. Помещая перед ним компенсатор К, можно исследовать свет, прошедший ячейку Керра. Ве­личина двойного лучепреломления n пропорц. квадрату напряжённости электрич. поля Е: n= nkE², где n — показатель преломления вещества в отсутствии поля, k — постоянная Кер­ра. Постоянной Керра иногда наз. также величину B=nk/ ( — длина световой волны). Постоянная Керра может быть положительной и отри­цательной. Её величина зависит от агрегатного состояния в-ва (для га­зов k~10 ^-15 ед. СГСЕ, для жидкостей k~10^-12 ед. СГСЕ), темп-ры (с уве­личением темп-ры постоянная Керра уменьшается), а также от структуры молекул в-ва.

Объяснение К. э. было дано франц. физиком П. Ланжевеном (1910) и нем. физиком М. Борном (1918). Электрич, поле ориентирует молекулы в-ва, об­ладающие дипольным моментом, вдоль поля,— ориентационный К. э., и индуцирует дипольный момент в моле­кулах (или атомах), не обладающих собственным дипольным моментом, поляризационный К. э. (см. Поляри­зуемость). В результате этого показатели преломления (и, следовательно, I скорости распространения в в-ве световых волн, поляризованных вдоль и поперёк Е) становятся различными, и возникает двойное лучепреломление.

В перем. электрич. поле величина ориентационного К. э. зависит от соотношения между частотой поля и скоростью ориентационной релакса­ции молекул (~10⁹ с^-1). Инерцион­ность поляризационного К. э. огра-

280


ничена временами ~10^-13 с. Поэтому при частотах электрич. поля вплоть до 10⁹—10¹³ Гц интенсивность света, проходящего через анализатор А, бу­дет обнаруживать модуляцию на уд­военной частоте (из-за квадратичности эффекта), а ячейка Керра будет рабо­тать как модулятор светового потока. Следствием квадратичности К. э. явл. также возникновение пост. составляю­щей двупреломления в перем. электрич. поле. Этот факт лежит в основе т. н. оптического К. э.— воз­никновения двупреломления под дей­ствием поля мощного (как правило, лазерного) оптич. излучения.

Магнитооптический К. э. состоит в том, что плоско поляризов. свет, отражаясь от намагниченного ферромагнетика, становится эллипти­чески поляризованным, при этом боль­шая ось эллипса поляризации повора­чивается на нек-рый угол по отноше­нию к плоскости поляризации падаю­щего света (см. Металлооптика). Это магнитооптическое явление - имеет природу, сходную с Фарадея эффек­том, и объясняется квантовой тео­рией.

• Волькенштейн М. В., Строение и физические свойства молекул, М.—Л., 1955; его же, Молекулярная оптика, М.—Л., 1951; Л а н д с б е р г Г. С., Оптика, 5 изд. М., 1976 (Общий курс физики).

Ю. Е. Светлов.

КЕРРА ЯЧЕЙКА, электрооптич. устройство, основанное на Керра эф­фекте, применяемое в кач-ве оптиче­ского затвора или модулятора света; наиболее быстродействующее устрой­ство для управления интенсивностью светового потока (скорость срабаты­вания ~10^-9—10^-13 с). К. я. со­стоит из сосуда с прозрачными ок­нами, заполненного пропускающим свет в-вом, напр. прозрачной жид­костью, в к-рую погружены два элект­рода, образующие плоский конденса­тор. Между электродами проходит линейно поляризованный световой луч (см. рис. в ст. Керра эффект), к-рый в отсутствии электрич. поля не про­пускается анализатором А (анализа­тор и поляризатор находятся в скре­щенном положении). При включении электрич. поля, составляющего угол 45° с направлениями электрич. поля поляризованных световых колебаний, в жидкости возникает двойное луче­преломление, световая волна оказы­вается эллиптически поляризованной и анализатор частично пропускает свет. В зависимости от заполняющей жидкости (применяются жидкости с большой постоянной Керра) и разме­ров ячейки макс. прозрачность дости­гается при напряжении на электро­дах 3—30 кВ. В нек-рых случаях в К. я. используют крист. и стекло­образные среды.

К. я. применяется в скоростной фото- и киносъёмке, в оптич. телефо­нии, в оптич. локации, геодезич. дальномерных устройствах и схемах управления оптич. квант. генерато­ров, в научных исследованиях.

• М у с т е л ь Е. Р., Парыгин В. Н.,

Методы модуляции и сканирования света,

М., 1970.

В. А. Замков.

К-ЗАХВАТ, захват ат. ядром эл-на с ближайшей к ядру орбиты—К-оболочки. См. Электронный захват.

КИКОИНА — НОСКОВА ЭФФЕКТ (фотомагнитоэлектрический эффект), возникновение электрич. поля в ос­вещённом ПП, помещённом в магн. поле. Электрич. поле перпендику­лярно магн. полю и потоку носителей тока (эл-нов проводимости, дырок), диффундирующих в ПП в направле­нии от освещённой стороны ПП, где поглощённые фотоны образуют элек­тронно-дырочные пары, к неосвещён­ной. К.— Н. э. наблюдается при резко неоднородной концентрации неоснов­ных носителей тока, что достигается при сильном поглощении света. От­крыт в 1933 сов. физиками И. К. Ки­коиным и М. М. Носковым.

• См. лит. при ст. Фотоэдс.

КИЛО... (франц. kilo..., от греч. chilioi — тысяча), приставка к наиме­нованию ед. физ. величины для об­разования наименования кратной еди­ницы, равной 1000 исходных ед. Обо­значения: к, k. Пример: 1 км=1000 м.

КИЛОВАТТ (кВт, kW), широко при­меняемая кратная ед. от ватта. 1 кВт=1000 Вт = 10¹⁰ эрг/с=101,97 кгс•м/с=1,36 л. с. =859,84 ккал/ч.

КИЛОВАТТ-ЧАС (кВт•ч, kW•h), вне­системная ед. энергии или работы, применяемая преим. в электротех­нике. 1 кВт•ч=3,6•10⁶ Дж.

КИЛОГРАММ (кг, kg), единица мас­сы, основная в СИ. К. равен массе междунар. прототипа, хранимого в Междунар. бюро мер и весов (в Севре, близ Парижа). Прототип К. сделан из платиново-иридиевого сплава (90% Pt, 10% Ir) в виде цилиндрич. гири (диаметром и высотой 39 мм); относит. погрешность сличений с прототипом эталонов-копий не превышает 2•10^-9. Широко применяется дольная ед.— грамм, равная 0,001 кг.

КИЛОГРАММ НА КУБИЧЕСКИЙ МЕТР (кг/м³, kg/m³), единица СИ плотности в-ва; 1 кг/м³ равен плот­ности однородного в-ва, 1 м³ к-рого содержит массу, равную 1 кг. 1 кг/м³= 10^-3 г/см³.

КИЛОГРАММ-МЕТР В СЕКУНДУ (кг•м/с, kg•m/s), единица СИ импульса (кол-ва движения); 1 кг•м/с равен импульсу тела массой 1 кг, движуще­гося поступательно со скоростью 1 м/с. КИЛОГРАММОМЕТР, см. Килограмм-сила-метр.

КИЛОГРАММ-СИЛА (кгс или кГ, kgf или kG), единица силы МКГСС системы единиц. 1 кгс=9,80665 нью­тона. В ряде европ. гос-в (ГДР, ФРГ, Австрия, Швеция и др.) для К.-с. официально принято название килопонд (kp).

КИЛОГРАММ-СИЛА-МЕТР (кгс•м или кГ•м, kgf•m или kG•m) (иногда эту ед. неправильно наз. килограммо­метр), единица энергии и работы МКГСС системы единиц. 1 кгс•м= 9,80655 Дж.

КИЛОПОНД, см. Килограмм-сила.

КИНЕМАТИКА (от греч. kinema, род. п. kinematos — движение), раз­дел механики, посвящённый изуче­нию геом. св-в движений тел, без учёта их масс и действующих на них сил. Методы и зависимости, устанав­ливаемые в К., используются при кинематич. исследованиях движений, в частности при расчётах передач дви­жений в разл. механизмах, машинах и др., а также при решении задач динамики. В зависимости от св-в изучаемого объекта К. разделяют на К. точки, К. тв. тела и К. непрерыв­ной изменяемой среды (деформируе­мого тв. тела, жидкости, газа).

Движение любого объекта в К. изучают по отношению к нек-рому телу (тело отсчёта), с к-рым связы­вают т. н. систему отсчёта (оси х, у, г на рис. 1), позволяющую опреде­лять положение движущегося объекта в разные моменты времени относи­тельно тела отсчёта.



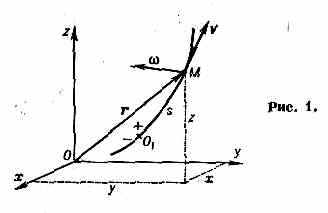
Выбор системы отсчёта в К. произволен и зависит от целей исследования. Напр., при изу­чении движения колеса вагона по от­ношению к рельсу систему отсчёта связывают с Землёй, а при изучении движения того же колеса по отноше­нию к кузову вагона — с кузовом и т. д. Движение рассматриваемого объекта считается заданным (извест­ным), если известны ур-ния (или графики, таблицы), позволяющие оп­ределить положение этого объекта по отношению к системе отсчёта в лю­бой момент времени.

Осн. задача К.— установление (при помощи тех или иных матем. методов) способов задания движения точек или тел и определение соответствующих кинематич. хар-к этих движений (тра­ектории, скорости и ускорения дви­жущихся точек, угл. скорости и угл. ускорения вращающихся тел и др.).

Движение точки может быть за­дано одним из трёх способов: вектор­ным, координатным или естественным. При векторном способе поло­жение точки по отношению к системе отсчёта определяется её радиусом-вектором r, проведённым от начала отсчёта до движущейся точки, а за­кон движения даётся векторным ур-нием: