От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Кирхгофа правила Кистевой разряд КЛАПЕЙРОНА УРАВНЕНИЕ (Кла­пейрона — Менделеева уравнение) Клапейрона — клаузиуса уравнение Карно цикла Классическая механика Классы кристаллов Клаузиуса неравенство Q — кол-во теплоты, поглощён­ной или отданной системой на беско­нечно малом участке кругового про­цесса при темп-ре Т Клаузиуса — моссотти фор­мула М — мол. масса в-ва,  — его плотность, n Клейна — гордона — фока уравнение Клин фотометрический Рис. 1. Схема прямопролётного двухрезонаторного клистрона. К-МЕЗОНЫ (каоны) С. С. Герштейн.

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КИРХГОФА ПРАВИЛА, устанавли­вают соотношения для токов и напря­жений в разветвлённых электрич. це­пях постоянного или квазистацио­нарного тока. Сформулированы Г. Р. Кирхгофом в 1847.

Первое К. п. вытекает из закона со­хранения заряда и состоит в том, что алгебр. сумма токов I_k, сходящихся в точке разветвления проводников (узле, рис., а), равна нулю: ^l_k=₁I_k=0 (l— число сходящихся токов); токи, при­текающие к узлу, считаются положи­тельными, вытекаю­щие из него — отри­цательными.

Второе К. п.: в любом замкну­том контуре, выде­ленном в сложной цепи проводников (рис., б), алгебр. сумма падений на­пряжений I_kR_k на отд. участках кон­тура (R_k—сопротив­ление k-того участка) равна алгебр. сумме эдс ξ_k в этом контуре:

^m_k=1=I_kR_k=^m_k=1ξ_k,

где m— число участков в замкнутом контуре (на рис. m=3, ξ₂=0). При этом следует выбрать положит. на­правления токов и эдс, напр. следует считать их положительными, если на­правление тока совпадает с направле­нием обхода контура по часовой стрел­ке, а эдс повышает потенциал в на­правлении этого обхода, отрицатель­ными — при противоположном на­правлении. Второе К. п. получается в результате применения Ома за­кона к разл. участкам замкнутой цепи.

К. п. позволяет рассчитывать слож­ные электрич. цепи, напр. определять силу и направление тока в любой части разветвлённой системы провод­ников, если известны сопротивления и эдс всех его участков. Для системы из n проводников, образующих r уз­лов, составляют n ур-ний: r-1 ур-ние для узлов на основе первого К. п. (ур-ние для последнего узла не явл. независимым, а вытекает из предыду­щих) и n-(r-1) ур-ний для независи­мых замкнутых контуров на основе второго К. п.; каждый из n проводни­ков в эти последние ур-ния должен войти хотя бы один раз. Т. к. при составлении ур-ний нужно учитывать направления токов в проводниках, к-рые заранее неизвестны, эти на­правления задаются произвольно; если при решении для к.-л. тока полу­чается отрицат. значение, то это озна­чает, что его направление противопо­ложно выбранному.

287


КИСТЕВОЙ РАЗРЯД, одна из форм электрического разряда в газах; возни­кает в случае сильно неоднородного поля при разряде с острия. По хар-ру элем. процессов К. р. близок к нач. стадии искрового разряда и отличается от него тем, что пучок искр (кисть), расходящийся от острия, не достигает второго электрода. Эта и ряд др. особенностей позволяют рассматри­вать К. р. как коронный разряд на острие с резко выраженными преры­вистыми явлениями. При понижении напряжения К. р. переходит в обыч­ный коронный разряд.

КЛАПЕЙРОНА УРАВНЕНИЕ (Кла­пейрона — Менделеева уравнение), зависимость между параметрами иде­ального газа (давлением р, объёмом V и абс. темп-рой Т), определяющими его состояние: pV=BT, где коэфф. пропорциональности В зависит от массы газа М и его мол. массы. Уста­новлен франц. учёным Б. П. Э. Кла­пейроном (В. Р. Е. Clapeyron) в 1834. В 1874 Д. И. Менделеев вывел ур-ние состояния для одного моля идеального газа: pV=RT, где R — универсаль­ная газовая постоянная. Если мол. масса газа , то

pV=(M/)RT, или PV=NkT,

где N — число ч-ц газа. К. у. пред­ставляет собой уравнение состояния идеального газа, к-рое объединяет Бойля — Мариотта закон, Гей-Люссака закон и Авогадро закон.

К. у.— наиболее простое ур-ние со­стояния, применимое с определ. сте­пенью точности к реальным газам при низких давлениях и высоких темп-pax (напр., к атм. воздуху, продуктам сгорания в газовых двига­телях), когда они близки по св-вам к идеальным газам.

КЛАПЕЙРОНА — КЛАУЗИУСА УРАВНЕНИЕ, термодинамич. ур-ние, относящееся к процессам перехода в-ва из одной фазы в другую (испаре­ние, плавление, сублимация, поли­морфное превращение и др.). Согласно К.— К. у., теплота фазового пере­хода L (напр., теплота испарения, теп­лота плавления) при равновесно про­текающем процессе определяется вы­ражением: L = Tdp/dT(V₂-V₁), где Т — темп-pa перехода (процесс изотерми­ческий), dp/dT — значение производ­ной от давления по темп-ре на кривой фазового равновесия, V₂-V₁ — из­менение объёма в-ва при переходе его из 1-й фазы во 2-ю.

К.—К. у. получено в 1834 Б.П.Э. Клапейроном из анализа Карно цикла для конденсирующегося пара, находя­щегося в тепловом равновесии с жид­костью. В 1850 нем. физик Р. Клаузи­ус (R. Clausius) усовершенствовал ур-ние и обобщил его на др. фазовые переходы. К.—К. у. применимо к лю­бым фазовым переходам, сопровождающимся поглощением или выделе­нием теплоты (т. н. фазовым перехо­дам I рода), и явл. прямым следствием условий фазового равновесия, из к-рых оно и выводится. К.— К. у. может служить для расчёта любой из величин, входящих в ур-ние, если остальные известны. В частности, с его помощью рассчитывают теплоты испарения, эксперим. определение к-рых сопряжено со значит. труднос­тями.

Часто К.— К. у. записывают отно­сительно производной dp/dT (или dT/dp): dp/dT=L/[T(V₂-V₁)]. Для процессов испарения и сублимации dp/dT выражает изменение давления насыщ. пара р с темп-рой Т, а для процессов плавления и полиморфного превращения dT/dp определяет изме­нение темп-ры перехода с давлением. Т. о., К.— К. у. явл. дифф. ур-нием кривой фазового равновесия в пере­менных р, Т. Для решения К.— К. у. необходимо знать, как изменяются с темп-рой и давлением величины L, V₁ и V₂, что представляет сложную задачу. Обычно эту зависимость ус­танавливают эмпирически и решают К.— К. у. численно.

При переходах, происходящих с по­глощением теплоты (в-во для осу­ществления перехода нагревается, и L>0), знак dp/dT определяется зна­ком разности (V₂-V₁). Если в-во во 2-й фазе занимает больший объём, чем в 1-й (т.е. V₂>V₁), то темп-ра перехода возрастает с увеличением давления и, наоборот, давление, при к-ром начинается переход, повышается с темп-рой. Такая зависимость харак­терна, напр., для процессов испаре­ния и сублимации.

При переходе в-ва из тв. состояния в жидкое условие L>0 выполняется, но возможны оба случая: V₂>V₁ и V₂1. В-ва, для к-рых реализуется второй случай, наз. а н о м а л ь н ы м и; для них плотность жидкости при темп-ре плавления больше плот­ности тв. фазы и dp/dT<0, т. е. темп-ра плавления понижается с ростом давления. К таким в-вам относятся вода, висмут, германий, нек-рые сорта чугуна и др. Понижение темп-ры плавления льда с увеличением дав­ления играет важную роль в ряде явлений. В природных условиях с ним связано, напр., сползание лед­ников.

К.— К. у. применимо не только к чистым в-вам, но также к р-рам и отдельным их компонентам. В по­следнем случае К.— К. у. связывает парц. давление насыщ. пара данного компонента с его парц. теплотой ис­парения.

• Курс физической химии, под ред. Я. И. Ге­расимова, 2 изд., т. 1, М., 1969.

КЛАССИЧЕСКАЯ МЕХАНИКА, ме­ханика, в основе к-рой лежат Ньютона законы механики и предметом изуче­ния к-рой явл. движение макроскопи­ческих материальных тел, совершае­мое со скоростями, малыми по сравнению со скоростью света. См. Ме­ханика.

КЛАССЫ КРИСТАЛЛОВ, то же, что точечные группы симметрии (см. Сим­метрия кристаллов). КЛАССЫ ТОЧНОСТИ средств измере­ний, обобщённая хар-ка средств из­мерений (мер, измерительных при­боров), служащая показателем уста­новленных для них гос. стандартами пределов осн. и дополнит. погреш­ностей и др. параметров, влияющих на точность. Напр., для концевых мер длины К. т. характеризует пре­делы допустимых отклонений от номин. размера и влияние изменений темп-ры, а также степень непарал­лельности рабочих поверхностей и отклонение их от идеальной плоскости. Введение К. т. облегчает стандарти­зацию средств измерений. Суще­ствующие обозначения К. т.— спо­соб выражения пределов допусти­мых погрешностей. Если пределы погрешностей даны в виде приве­дённой погрешности (т. е. в % от верх. предела измерений, диапазона измерений или длины шкалы при­бора), а также в виде относит. погреш­ности (т. е. в % от действит. значения величины), то К. т. обозначают чис­лом, соответствующим значению осн. погрешности. Напр., К. т. 0,1 соот­ветствует осн. погрешности 0,1%. Многие показывающие приборы (ам­перметры, вольтметры, манометры и др.) нормируются по приведённой по­грешности, выраженной в % от верх. предела измерений. В этих случаях применяется ряд К. т.: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. При нормировании по относит. погрешности обозначе­ние К. т. заключают в кружок. Для гирь, мер длины и приборов, для к-рых предел погрешности выражают в единицах измеряемой величины, К. т. принято обозначать номером (1-й, 2-й и т. д.— в порядке сниже­ния К. т.). Ряды К. т., их обозна­чения и соответствующие требова­ния к средствам измерений включаются в государственные стандарты на отдельные их виды.

• ГОСТ 8.401—80. Государственная систе­ма обеспечения единства измерений. Классы точности средств измерений. Общие тре­бования, М., 1981; Ш и р о к о в К. П., Рабинович С. Г., О классах точности средств измерений, «Измерительная техни­ка», 1969, № 4, с. 3. К. П. Широт.

КЛАУЗИУСА НЕРАВЕНСТВО, выражает теорему термодинамики, со­гласно к-рой для любого кругового процесса (цикла), совершённого систе­мой, выполняется неравенство:



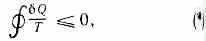
где  Q — кол-во теплоты, поглощён­ной или отданной системой на беско­нечно малом участке кругового про­цесса при темп-ре Т (в том случае, когда теплота подводится к рабочему телу, Q считают положительным, а когда отводится — отрицательным), Необратимому циклу, т. е. циклу,

288


включающему хотя бы один необра­тимый процесс, соответствует знак неравенства. Циклу, состоящему из обратимых процессов (в частности, Карно циклу), отвечает знак равен­ства. Подынтегральное выражение Q/T для обратимого процесса пред­ставляет собой полный дифференциал термодинамич. ф-ции, к-рую Р. Клау­зиус назвал энтропией (т. е. Q/T=dS, где S — энтропия системы). В общем случае Q/TsdS, а это не­равенство также наз. К. н. Согласно (*), энтропия системы в результате осуществления цикла либо возрастает, либо остаётся неизменной. Истори­чески К. н. (Клаузиус, 1854) явилось первой матем. формулировкой второго начала термодинамики как закона возрастания энтропии. После статистич. обоснования австр. физиком Л. Больцманом этого закона (1877) он стал наиболее фундам. выражением второго начала термодинамики.

КЛАУЗИУСА — МОССОТТИ ФОР­МУЛА, выражает приближенную связь между статич. диэлектрической проницаемостью к неполярного ди­электрика и поляризуемостью а его молекул, атомов или ионов и от их числа N в 1 см³ (ч-цы одного сорта):



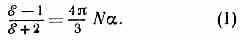
Часто К.— М. ф. записывают в виде:



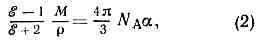
где М — мол. масса в-ва,  — его плотность, n_a — Авогадро постоян­ная. Правую часть (2) иногда назы­вают мол. рефракцией. К.— М. ф. установлена нем. физ. Р. Клаузиусом (R. Clausius), развившим идеи итал. учёного О. Ф. Моссотти (О. F. Mossotti).

К.— М. ф. хорошо выполняется для неполярных газов при низких (~200— 500 мм рт. ст. или 2•10⁵—5•10⁵ Па), средних (от 500 мм рт. ст. до 5 атм) давлениях и приближённо при по­вышенных (>5—10 атм) давлениях. В случае динамич. диэлектрич. про­ницаемости и чисто электронной поля­ризуемости для частот оптич. диапа­зона К.— М. ф. переходит в Лоренц— Лоренца формулу. •См. лит. при ст. Диэлектрики.

КЛЕЙНА — ГОРДОНА — ФОКА УРАВНЕНИЕ, квантовое релятив. ур-ние для ч-ц с нулевым спином. Исторически К.— Г.— Ф. у. явл. пер­вым релятив. ур-нием квант. меха­ники для волн. ф-ции ч-цы (); оно было предложено в 1926 австр. физи­ком Э. Шредингером (как релятив. обобщение Шредингера уравнения) и независимо от него швед. физиком 0. Клейном (О. Klein), В. А. Фоком, нем. физиком В. Гордоном (W. Gor­don) и др. Для свободной ч-цы К.— Г.— Ф. у. записывается в виде:




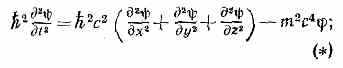
ему соответствует релятив. соотноше­ние между энергией ξи импульсом р ч-цы: ξ²=p²c³+m²c⁴ (m — масса ч-цы). Решением ур-ния (*) явл. ф-ция (х, у, z, t), зависящая только от координат (х, у, z) и времени (t). Следовательно, ч-цы, состояние к-рых описывается этой ф-цией, не обладают никакими дополнит. внутр. степе­нями свободы, т. е. действительно явл. бесспиновыми (к таким ч-цам относятся, напр., - и К-мезоны).

Анализ ур-ния показал, что его решение () принципиально отли­чается по своему физ. смыслу от обыч­ной волн. ф-ции как амплитуды ве­роятности нахождения ч-цы в задан­ном месте пр-ва в заданный момент времени: (х, у, z, t) не определяется однозначно значением  в нач. мо­мент времени (такая однозначная за­висимость постулируется в квант. механике), и, более того, выражение вероятности состояния наряду с по­ложит. значениями может принимать также и лишённые физ. смысла отрицат. значения. Поэтому сначала от К.— Г.— Ф. у. отказались. Однако в 1934 швейц. физик В. Паули и амер. физик В. Ф. Вайскопф нашли правильную интерпретацию этого ур-ния в рамках квантовой теории поля (они рассмотрели его как ур-ние поля, аналогичное ур-ниям Макс­велла для эл.-магн. поля, и проквантовали; при этом  стало оператором).

• См. лит. при ст. Квантовая теория поля.

М. А. Либерман.

КЛИН ФОТОМЕТРИЧЕСКИЙ, уст­ройство для ослабления светового по­тока, применяемое в фотометрии. Представляет собой клин из ахрома­тического (имеющего нейтрально-се­рый цвет) в-ва, коэфф. поглощения к-рого не зависит от длины световой волны (спец. стек­ло, желатиновая плёнка, содержа­щая коллоидные графит или серебро, и др.). Степень ос­лабления светового потока к.-л. уча­стком К. ф. опре­деляется его опти­ческой плотностью D=lg(Ф/Ф₀), где Ф/Ф₀ — отношение падающего на клин и прошедшего через него световых по­токов. Оптич. плотность может изме­няться вдоль клина либо непрерывно, увеличиваясь пропорц. его толщине l (непрерывный К. ф.), либо сту­пенями на определ. величину (с т у п е н ч а т ы й К. ф.). К. ф. характе­ризуют константой k, к-рая у непре­рывного клина равна разности оптич. плотностей любых его точек, отстоя­щих друг от друга на ед. длины, а у ступенчатого — разности оптич. плотностей двух соседних полей. Ли­нейная зависимость l и D от расстоя­ния х между началом клина О и рас­сматриваемым участком АС (рис.)



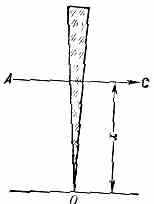
позволяет наносить на К. ф. равно­мерную шкалу, градуируемую по кон­станте k.

Перемещением клина, фиксируемым по шкале, можно менять его коэфф. пропускания =Ф/Ф₀=(1-)²•10^-kx, где  — коэфф. отражения от каждой поверхности клина.

КЛИСТРОН [от греч. klyzo — ударяю и (элек)трон], электронный прибор для усиления и генерирования колеба­ний СВЧ. Существуют прямопролётные К. (двух- и многорезонаторные) и отражательные К.; сверхминиатюрные



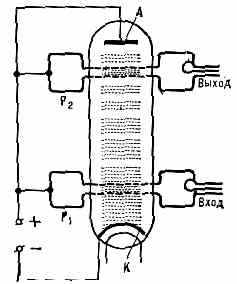
Рис. 1. Схема прямопролётного двухрезонаторного клистрона.


отражательные К. наз. м и н и т р о н а м и. Принцип действия двухрезонаторного прямопролётного К. состоит в следующем: эл-ны, эмиттируемые катодом К, ускоряются электрич. по­лем и, пролетев через два объёмных резонатора Р₁ и Р₂, попадают на коллектор А (рис. 1). В первом резо­наторе p₁ поток эл-нов модулируется по скорости. Эл-ны группируются в сгустки, к-рые влетают во второй ре­зонатор Р₂ в момент, когда электрич. поле эл.-магн. колебаний, возбуждён­ных в нём, тормозит эл-ны, в резуль­тате чего энергия эл-нов, полученная ими от источника пост. напряжения, переходит в энергию эл.-магн. поля, и эл.-магн. колебания усиливаются. Если двухрезонаторный К. работает как усилитель, то усиливаемые коле­бания подводятся к p₁ и снимаются с Р₂. В генераторах оба резонатора связаны по СВЧ полю.

Двухрезонаторные К. появились в 1932—35. В совр. технике их исполь­зуют редко, в осн. для генерации колебаний мощностью в 1—5 Вт. В кач-ве мощных усилителей колеба­ний СВЧ с большим коэфф. усиления (неск. десятков дБ) используются прямопролётные К. с большим числом резонаторов.

Как генераторы малой мощности «1 Вт) используются отражательные К., в к-рых эл-ны, пролетев резона­тор, тормозятся и возвращаются об­ратно, отражаясь в поле отражателя (рис. 2). При этом они группируются

289




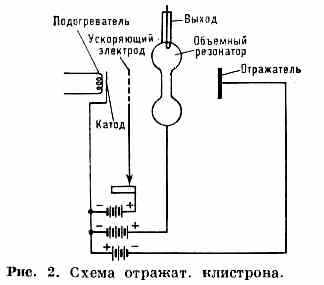
в сгустки, при втором пролёте резо­натора тормозятся и отдают энергию эл.-магн. полю. Изменяя напряжение на отражателе, можно в нек-рых пре­делах регулировать частоту генера­ции. К. генерируют колебания с час­тотой до 2•10²ГГц.

• Лебедев И. В., Техника и приборы СВЧ, т. 2, М., 1972; Б у н и н Г. Г., Васенькин В. А., Отражательные клист­роны, М., 1966; К а л и ш П. Р., Я р о ч к и н Н. И., Усилительные клистроны, М., 1967; Голант М. Б., Бобровский Ю. Л., Генераторы СВЧ малой мощности, М., 1977.

К-МЕЗОНЫ (каоны), группа неста­бильных элем. ч-ц из двух заряженных (К⁺ , К^~-) и двух нейтральных (К°, К^~°) ч-ц с нулевым спином и массой, прибл. в 970 раз большей массы эл-на (в энергетич. ед. масса К⁺ равна 493,7 МэВ, а К°—497,7 МэВ). К-м. участвуют в сильном вз-ствии, т. е. явл. адронами: они не имеют барионного наря­да и обладают ненулевым значением квант. числа странности (S): у К⁺ и К° S = + l, а у К^- и К^~° (являющихся античастицами К⁺ , К°) S=-1. Сов­местно с гиперонами К-м. относятся к странным частицам. К⁺ и К° объе­диняются в изотопич. дублет (см. Изотопическая инвариантность) и рас­сматриваются как разл. зарядовые состояния одной ч-цы с изотопич. спином I=¹/₂. Аналогичную группу составляют К^- и К^~°.

Согласно модели кварков, в состав К^- и К^~° входит s-кварк с S=-1, a в состав К⁺ и К°— антикварк s^~ с S=+1 (см. Элементарные частицы).

Открытие К-м.. связано с работами большого числа учёных. В 1947—51 в косм. лучах были открыты ч-цы, массы к-рых были прибл. одинако­выми, а способы распада — разными: -мезоны, распадающиеся на два -мезона, и -мезоны, распадающиеся на три -мезона. В 1954 эти ч-цы стали получать с помощью ускорителей, и тщат. измерения масс и времён жиз­ни показали, что во всех случаях наблюдались разл. способы распада одних и тех же ч-ц, названных К-м.

Сильное взаимодейст­вие К-м. Закон сохранения стран­ности в сильном вз-ствии накладывает характерный отпечаток на про­цессы сильного вз-ствия с участием К-м. Так, К⁺ и К° (.S=1) рождаются при столкновениях «нестранных» ч-ц— -мезонов и нуклонов только совм. с гиперонами или К^-, К^~°, имеющими отрицат. значение странности. Силь­ное вз-ствие может вызывать, напр., процессы:



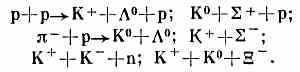
Во всех этих реакциях суммарная странность в конечном состоянии рав­на 0 в соответствии с тем, что в нач. состоянии S=0. К^- и К^~° рождаются при столкновении нестранных ч-ц либо совместно с К⁺ или К°, либо с антигиперонами, странность к-рых поло­жительна. Рождение гиперонов в пуч­ках К⁺ , К° менее вероятно, чем в пуч­ках К^-, К^~°, т. к. оно требует появ­ления совм. с гипероном неск. допол­нит. К⁺ или К°. Поэтому медленные К⁺ , К° слабее взаимодействуют с в-вом, чем К^-, К^~°.

Слабое взаимодействие К - м. Распады К-м. обусловлены сла­бым вз-ствием и происходят с изме­нением странности на единицу. Они могут осуществляться разл. способа­ми, напр. K^±^±+v_(v^~_) (63,5%); ^±+° (21,16%). Время жизни К⁺ и К составляет 1,2•10^-8 с. В распа­дах К-м. не сохраняются пространств. чётность и зарядовая чётность, что проявляется, напр., в возможности распада как на два, так и на три -мезона.. Рисунок иллюстрирует про­цессы сильного и слабого вз-ствий К-м.



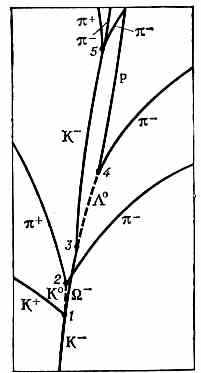
Схематич. изоб­ражение фотогра­фии, полученной в водородной пу­зырьковой каме­ре, иллюстрирую­щее процессы вз-ствий К-мезонов. В точке 1 за счёт сильного вз-ствия проис­ходит реакция

K^-+р^-+ К⁺+К°, в к-рой сохраняется странность. Обра­зовавшиеся ч-цы распадаются в результате сла­бого вз-ствия с изменением странности на 1: К°⁺+^- (в точке 2); ^--°+К^- (в точке 3); °p+^- (в точке 4); К^-⁺+^-+^- (в точке 5). Треки ч-ц искривлены, т. к. камера находится в магн. поле. Пункти­ром обозначены треки нейтр. ч-ц, не остав­ляющих следа в камере.


Специфические свойст­ва нейтральных К-м. К° и К^~°, обладая разл. значениями стран­ности, по-разному участвуют в сильном вз-ствии. Однако слабое вз-ствие, меняющее странность, делает возмож­ными взаимные превращения K°K^~0. Т. к. странность в слабом вз-ствии меняется на единицу, то переходы К° К^~° с │S│=2 происходят в два этапа (во 2-м порядке по слабому вз-ствию). Наличие таких переходов между ч-цей и античастицей обуслов­ливает уникальные св-ва нейтр. К-м. Для любых других ч-ц подобные пере­ходы запрещены строгими законами сохранения, напр. электрич. или ба­рионного заряда. В вакууме благода­ря переходам КК^~0 состояниями, имеющими определённые энергию и время жизни, будут не К° и К^~°, а две квантовомеханич. суперпозиции этих состояний, к-рые соответствуют ч-цам с разными массами и разными време­нами жизни: т. н. д о л г о ж и в у щ е м у К⁰_L-мезону и к о р о т к о ж и в у щ е м у К⁰_S-мезону. Время жизни К" составляет _L5,18•10^-8с, a k0s—_S0,89•10^-10 с. Их массы равны примерно массе К°; разность масс K°_L и k⁰_s пропорциональна амп­литуде перехода К°К^~° и очень мала (~h/_S3•10^-6 эВ). Осн. способы распада k⁰_s и К⁰_L,



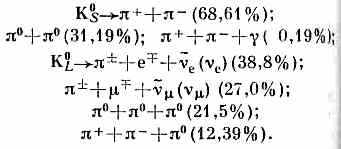
Т. о., в то время как в процессах, вызываемых сильным вз-ствием, про­являются состояния К° и К^~°, обла­дающие определ. значениями стран­ности, в процессах слабого вз-ствия как ч-цы проявляются состояния К⁰_L и К⁰_S. Состояния K⁰_S и К⁰_L близки к суперпозициям состояний, к-рые наз. К⁰₁ и К⁰₂:



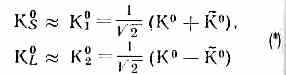
[в (*) через K°_S, K°_L, К⁰, К^~0 и т. д. обозначены волн. ф-ции соответст­вующих ч-ц; 1/2 — нормирующий множитель], т. е. К⁰_S и К⁰_L прибл. на 50% «состоят» из К° и на 50% из К^~0. Аналогично К° и К^~° прибл. на 50% «состоят» из k⁰_s и на 50% из К⁰_L. Поэтому распады К° и К^~° происходят прибл. на 50% по схеме распадов K⁰_S и прибл. на 50% по схеме К⁰_L. То, что состояния К° и К^~° представляют суперпозицию состояний К⁰_S и К⁰_L с разными массами и временами жиз­ни, приводит к появлению своеоб­разных осцилляции («биений»), ана­логичных биениям в системе, состоя-

290


щей из двух связанных между собой маятников, имеющих одинаковые час­тоты колебаний. Так, К°, возникая в результате сильного вз-ствия, на нек-ром расстоянии от точки рожде­ния частично превращается за счёт слабого вз-ствия в К^~° и оказывается способным вызывать яд. реакции, ха­рактерные для К^~° и запрещённые для К°, напр. реакцию К^~0+р⁰+⁺. Другое своеобразное явление — т. н. регенерация k⁰_s при прохождении через в-во долгоживущих К⁰_L-мезонов. На достаточно больших расстоя­ниях от места образования пучка К° (или К^~°) он состоит практически толь­ко из К⁰_L, т. к. короткоживущие К⁰_S распадаются раньше. Поэтому на та­ких расстояниях наблюдаются лишь распады, характерные для K⁰_L. Ка­залось бы, k⁰_s не могут вновь по­явиться в пучке. Однако при про­хождении пучка К⁰_L через слой в-ва из-за различия во вз-ствиях с в-вом К° и К^~°, «составляющих» k⁰_l, изме­няется относит. состав пучка и по­является добавка K⁰_S с характерными для них распадами.

Комбинации К⁰₁ и К⁰₂ обладают определ. симметрией относительно опе­рации комбинированной инверсии — комбинированной чётностью (или СР-чотностью): у К⁰¹ СР=+1, у К⁰₂ СР=-1. Поэтому К⁰₁ может распадаться на два  (систему, обладающую теми же ев-вами относительно операции СР, что и К⁰₁), а К⁰₂ не может. Т. к. вероятность распада на двазначи­тельно превышает вероятности др. каналов распада, большое различие во временах жизни К0_L и К⁰_S счита­лось указанием на существование в природе симметрии относительно операции комбиниров. инверсии, а состояния k⁰_s и k⁰_l отождествлялись с K⁰₁ и К⁰₂. Однако в 1964 было уста­новлено, что К⁰_L с вероятностью прибл. 0,2% распадается на два . Это сви­детельствует о нарушении СР-симметрии и об отличии состояний k⁰_s и К⁰_L от K⁰₁ и К⁰₂. Другое проявление нарушения СP-инвариантности — за­рядовая асимметрия распадов K⁰_L^-+e⁺(_:⁺)+v^~_e(v^~_) и К⁰_L⁺ +e^-(^-)+v^~_e(v^~_): вероятность первого распада больше, чем второго, прибл. на 10^-3. Это означает, что k⁰_l не явл. истинно нейтральной частицей. При­рода сил, нарушающих СР-симметрию, не выяснена.

• Марков М. А., Гипероны и К-мезоны, М., 1958; Д а л и ц Р., Странные частицы и сильные взаимодействия, пер. с англ., М., 1964; Окунь Л. Б., Слабое взаимодействие элементарных частиц, М., 1963; Л и Ц., В у Ц., Слабые взаимодействия, пер. с англ., М., 1968; Газиорович С., Физика эле­ментарных частиц, пер. с англ., М., 1969: Э д е р Р. К., Ф а у л е р Э. К., Странные частицы, пер. с англ., М., 1966.

С. С. Герштейн.