От лат cavitas пустота), образование в капельной жидкости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац
| Вид материала | Документы |
- Вывихи. Переломы, 241.71kb.
- От лат evaporo испаряю и греч grapho пишу), метод получения изображений объектов, 2696.94kb.
- Реферат от лат rеfеrо "сообщаю", 198.27kb.
- Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
- Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
- Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
- Реферат от лат. «сообщать», 61.18kb.
- Лекция. Взаимосвязанные рынки, 285.49kb.
- Реферат Реферат, 36.91kb.
- Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.
КОВАРИАНТНОСТЬ (от лат. со — совместно и varians — изменяющийся), форма записи физ. величин и ур-ний, непосредственно отражающая хар-р их изменения (векторный, спинорный, тензорный и т. д.) при преобразованиях системы пространственно-временных координат. Примером может служить представление энергии ξ и импульса р в относительности теории в виде четырёхмерного импульса р с компонентами р, =0, 1, 2, 3 (р0=ξ/с, p1=px, р2=pу, p3=pz), изменяющегося при Лоренца преобразованиях как четырёхмерный вектор. В спец. теории относительности ур-ния, записанные в ковариантной форме, имеют одинаковый вид во всех инерциальных системах отсчёта. Широко К. используется в общей теории относительности (теории тяготения), где она означает неизменность вида ур-ний относительно любых преобразований пространственно-временных координат.
А. В. Ефремов.
КОГЕЗИЯ (от лат. cohaesus — связанный, сцепленный), сцепление друг с другом частей одного и того же тела, обусловленное действием сил межмолекулярного взаимодействия, водородной связи и (или) химической связи между составляющими его молекулами (атомами, ионами) и приводящее к объединению этих частей в единое целое с наибольшей прочностью. Силы К. резко убывают с расстоянием, незначительны в газах и наиб. велики в тв. телах. К. характеризует прочность тела, лишённого дефектов по отношению к деформациям.
КОГЕРЕНТНОСТЬ (от лат. cohaerens— находящийся в связи), согласованное протекание во времени и в пр-ве неск. колебат. или волн. процессов, проявляющееся при их сложении. Колебания наз. когерентными, если разность их фаз остаётся постоянной (или закономерно изменяется) во времени и при сложении колебаний определяет амплитуду суммарного колебания. Гармонич. колебание описывается выражением:
Р(t)=Acos(t+), (1)
где Р — изменяющаяся величина (смещение маятника, напряжённость электрич. и магн. полей и т. д.), а амплитуда А , частота со и фаза — константы. При сложении двух гармонич. колебаний с одинаковой частотой со, но разными амплитудами a1 и А2 и фазами 1 и 2 образуется
гармонич. колебание той же частоты. Амплитуда результирующего колебания
Ар =(A21+A22+2A1A2cos(1-2)) (2)
может изменяться в пределах от A1+A2 до ai-A2 в зависимости от разности фаз 1-2 (рис.).
В действительности идеально гармонич. колебания неосуществимы. В реальных колебат. процессах амплитуда, частота и фаза колебаний могут непрерывно хаотически изменяться во времени. Если фазы двух колебаний 1 и 2 изменяются беспорядочно, но
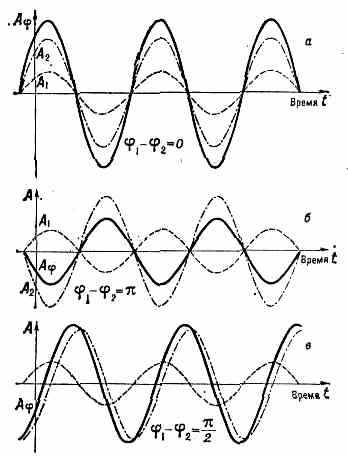
Сложение двух гармонич. колебаний (пунктир) с амплитудами a1 и A2 при разл. разностях фаз. Результирующее колебание — сплошная линия.
их разность 1-2 остаётся постоянной, то амплитуда суммарного колебания определяется разностью фаз складываемых колебаний, т. е. колебания когерентны. Если разность фаз двух колебаний изменяется очень медленно, то в этом случае колебания остаются когерентными лишь в течение нек-рого времени, пока их разность фаз не успела измениться на величину, сравнимую с я.
Если сравнивать фазы одного и того же колебания в разные моменты времени, разделённые интервалом т, то при достаточно большом т случайное изменение фазы колебания может превысить л. Это означает, что через время т гармонич. колебание «забывает» свою первонач. фазу и становится некогерентным «самому себе». С ростом т К. обычно ослабевает постепенно. Для количеств, хар-ки этого явления вводят ф-цию R (), наз. функцией корреляции. Результат сложения двух колебаний, полученных от одного источника и задержанных друг относительно дру-
291
га на время , можно представить с помощью R () в виде:
Ар = (A21+A22+2A1A2R ()cos) , (3)
где — ср. частота колебания. Ф-ция R()=1 при =0 и обычно спадает до 0 при неогранич. росте . Значение т, при к-ром R()=0,5, наз. временем когерентности или продолжительностью гармонич. цуга. По истечении одного гармонич. цуга колебаний он как бы заменяется другим с той же частотой, но с другой фазой.
Хар-р и св-ва колебат. процесса существенно зависят от условий его возникновения. Напр., свет, излучаемый газовым разрядом в виде узкой спектр. линии, может быть близок к монохроматическому. Излучение такого источника складывается из волн, посылаемых разл. ч-цами независимо друг от друга и поэтому с независимыми фазами (спонтанное излучение). В результате амплитуда и фаза суммарной волны хаотически изменяются с характерным временем, равным времени К. Изменения амплитуды суммарной волны велики: от 0, когда исходные волны гасят друг друга, до макс. значения, когда соотношение фаз исходных волн благоприятствует их сложению. Колебания, возникающие в автоколебат. системе, напр. в ламповом или транзисторном генераторах, лазере, имеют др. структуру. В первых двух частота и фаза колебаний хаотически изменяются, но результирующая амплитуда поддерживается постоянной. В лазере все ч-цы излучают согласованно (вынужденное излучение), синфазно с колебанием, установившимся в резонаторе. Соотношения фаз слагающих колебаний всегда благоприятны для образования устойчивой амплитуды суммарного колебания. Термин «К.» иногда означает, что колебание порождено автоколебат. системой и имеет стабильную амплитуду.
При распространении плоской эл.-магн. волны в однородной среде фаза колебаний в к.-н. определ. точке пр-ва сохраняется только в течение времени К. 0. За это время волна распространяется на расстояние c0. При этом колебания в точках, удалённых друг от друга на расстояние, большее c0, вдоль направления распространения волны, оказываются некогерентными. Расстояние, равное c0 вдоль направления распространения плоской волны, наз. длиной К. или длиной цуга.
Идеально плоская волна неосуществима, как и идеально гармонич. колебание. В реальных волн. процессах амплитуда и фаза колебаний изменяются не только вдоль направления распространения волны, но и в плоскости, перпендикулярной этому на-
правлению. Случайные изменения разности фаз в двух точках, расположенных в этой плоскости, увеличиваются с расстоянием между ними. К. колебаний в этих точках ослабевает и на нек-ром расстоянии l, когда случайные изменения разности фаз становятся сравнимыми с я, исчезает. Для описания когерентных св-в волны в плоскости, перпендикулярной направлению её распространения, применяют термины площадь К. и пространственная К., в отличие от временной К., связанной со степенью монохроматичности волны. Количественно пространств. К. также можно характеризовать ф-цией корреляции RI(l). Условие Rf(l)=0,5 определяет размер или радиус К., к-рый может зависеть от ориентации отрезка l в плоскости, перпендикулярной направлению распространения волны. Всё пр-во, занятое волной, можно разбить на области, в каждой из к-рых волна сохраняет К. Объём такой области (объём К.) принимают равным произведению длины цуга на площадь фигуры, ограниченной кривой RI(l)=0,5RI(0).
Нарушение пространств. К. связано с особенностями процессов излучения и формирования волн. Напр., нагретое тело излучает совокупность сферич. волн, распространяющихся по всем направлениям. По мере удаления от теплового источника конечных размеров волна приближается к плоской. На больших расстояниях от источника размер К. равен l,22r/, где r — расстояние до источника, — размер источника. Для солн. света размер К. равен 30 мкм. С уменьшением утл. размера источника размер К. растёт. Это позволяет определить размер звёзд по размеру площади К. приходящего от них света. Величину / наз. углом К. С удалением от источника интенсивность света убывает пропорц. 1/r2. Поэтому с помощью нагретого тела нельзя получить интенсивное излучение, обладающее большой пространств. К. Световая волна, излучаемая лазером, формируется в результате вынужденного излучения во всём объёме активного в-ва. Поэтому пространств. К. лазерного излучения сохраняется во всём поперечном сечении луча.
Понятие «К.», возникшее первоначально в классич. оптике как хар-ка, определяющая способность света к интерференции (см. Интерференция света), широко применяется при описании колебаний и волн любой природы. Благодаря квант. механике, распространившей волн. представления на все процессы в микромире, понятие «К.» стало применяться к пучкам эл-нов, протонов, нейтронов и др. ч-ц. Здесь под К. понимают упорядоченные согласованные и направленные движения большого кол-ва квазинезависимых ч-ц. Понятие «К.» проникло также в теорию тв.
тел (напр., гиперзвуковые фононы, см. Гиперзвук) и квант. жидкостей. После открытия сверхтекучести жидкого гелия появилось понятие «К.», означающее, что макроскопич. кол-во атомов жидкого сверхтекучего гелия может быть описано единой волн. ф-цией, имеющей одно собств. значение, как будто это одна ч-ца, а не ансамбль огромного числа взаимодействующих ч-ц.
• Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); М а р т и н с с е н В., Ш п и л л е р Е., Что такое когерентность, «Природа», 1968, № 10; К л а у д е р Дж., С у д а р ш а н Э., Основы квантовой оптики, пер. с англ., М., 1970; Перина Я., Когерентность света, пер. с англ., М., 1974.
А. В. Францессон,
КОКРОФТА — УОЛТОНА ГЕНЕРАТОР, каскадный генератор последоват. питания с ёмкостной связью.
КОЛЕБАНИЙ И ВОЛН ТЕОРИЯ, область науки, исследующая колебат. и волн. явления в системах разл. природы. В колебат. и волн. процессах разл. природы обнаруживаются одни и те же закономерности, к-рые описываются одними и теми же матем. и физ. моделями и исследуются общими методами. К. и в. т. устанавливает общие св-ва колебат. и волн. процессов в реальных системах и определяет связь между параметрами системы и её колебательными (волновыми) хар-ками, независимо от св-в конкретной системы, связанных с проявлением её природы (физической, химической и пр.). Поэтому результаты, полученные при исследовании колебаний и волн, напр. в механике, могут быть перенесены в оптику или радиотехнику. Так, при создании параметрических генераторов света использовались идеи и методы, выработанные при исследовании параметрич. колебаний в радиотехнике.
Изучение любого волн. или колебат. процесса начинается с идеализации реальной системы, т. е. с построения модели и составления для неё соответствующих ур-ний. Идеализации одних и тех же систем могут быть различны в зависимости от того, какое явление исследуется. Справедливость принятых идеализации оценивается путём сравнения результатов теории, построенной на основании данной модели, с результатами анализа более общей модели или с поведением реальной системы — экспериментом. Напр., когда речь идёт только о нахождении условий раскачки качелей при периодич. изменении их длины, модель может быть совсем простой — линейный осциллятор с периодически меняющейся собств. частотой. Когда же необходимо ответить на вопрос об амплитуде установившихся колебаний таких качелей, нужно уже учитывать нелинейность (зависимость частоты колебаний качелей от амплитуды колебаний), в результате чего приходим к модели физ. маятника, т. е. нелинейного осциллятора с периодически изменяемым параметром.
292
Понятия и представления К. и в. т. относятся либо к явлениям (резонанс, автоколебания и т. д.), либо к моделям (линейная и нелинейная система, системы с сосредоточенными параметрами или системы с распределёнными параметрами, система с одной или неск. степенями свободы и пр.). На основе сложившихся представлений К. и в. т. можно связать те или иные явления в конкретной системе с её хар-ками, не решая задачи всякий раз заново. Напр., преобразование энергии одних колебаний в другие в слабонелинейной системе (волны на воде, эл.-магн. волны в ионосфере, колебания маятника на пружине) возможно только в случае, когда выполнены определ. резонансные условия между собств. частотами подсистемы.
Методы К. и в. т.— это методы анализа ур-ний, описывающих модели реальных систем. Большинство из них совпадают с методами качеств. теории дифф. ур-ний (метод фазового пр-ва, метод отображений Пуанкаре и др.), с асимптотич. методами решения дифференциальных и иных ур-ний (метод ван дер Поля, метод усреднения и т. д.). Специфика методов К. и в. т. состоит в том, что при изучении моделей колебат. или волн. явлений интересуются, как правило, общими св-вами решений соответствующих ур-ний.
Осн. разделы К. и в. т.— теория устойчивости линеаризованных систем, теория параметрич. систем, теория автоколебат. и автоволн. процессов, теория ударных волн и солитонов, кинетика колебаний и волн в системах с большим числом степеней свободы, теория стохастич. систем — систем со сложной динамикой. Если «классическая» К. и в. т. рассматривала в осн. системы с простой динамикой и поэтому изучала, как правило, лишь регулярные (периодические) колебания и волны, то в совр. теории усилился интерес к статистич. задачам, связанным с анализом процессов «рождения» статистики в детерминиров. системах. В этих задачах, а также при исследовании сложных колебат. и волн. структур в неравновесных средах совр. К. и в. т. перекрывается с синергетикой.
• См. лит. при статьях Колебания и Волны.
М. И. Рабинович.
КОЛЕБАНИЯ, движения или процессы, обладающие той или иной степенью повторяемости во времени. К. свойственны всем явлениям природы: пульсирует излучение звёзд, внутри к-рых происходят циклич. яд. реакции; с высокой степенью периодичности вращаются планеты Солн. системы; движение Луны вызывает приливы и отливы на Земле; в земной ионосфере и атмосфере циркулируют потоки заряж. и нейтр. ч-ц; ветры возбуждают К. и волны на поверхности водоёмов и т. д. Внутри любого живого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы, напр. с удивительной надёжностью бьётся человеческое сердце, даже психика людей подвержена К. В виде сложнейшей совокупности К. ч-ц и полей (эл-нов, фотонов, протонов и др.) можно представить «устройство» микромира.
В технике К. либо выполняют определённые функцией, обязанности (маятник, колебат. контур, генератор К. и др.), либо возникают как неизбежное проявление физ. св-в (вибрации машин и сооружений, неустойчивости и вихревые потоки при движении тел в газах и т. д.).
В физике выделяются К. механические, электромагнитные и их комбинации. Это обусловлено той исключит. ролью, к-рую играют гравитац. и эл.-магн. вз-ствия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механич. К. плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых К. электрич. и магн. полей, воспринимаемых нами как свет, мы получаем б. ч. прямой информации об окружающем мире.
К. любых физ. величин почти всегда связаны с попеременным превращением энергии одного вида в энергию другого вида. Так, при отклонении маятника (груза на нити, рис. 1) от положения равновесия увеличивается потенц. энергия груза, запасённая им в поле тяжести; если груз отпустить, он падает, вращаясь около точки подвеса как около центра; в крайнем нижнем положении потенц. энергия превращается в кинетическую, и груз проскакивает это равновесное положение, увеличивая снова потенц. энергию. Далее процесс перекачки энергии повторяется, пока рассеяние (диссипация) энергии, обусловленное, напр., трением, не приводит к полному прекращению К.
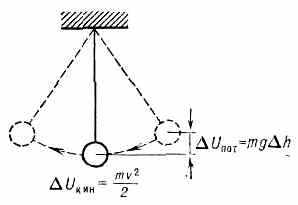
Рис. 1. Схема колебаний маятника: m — масса груза; g — ускорение силы тяжести; h — высота подъёма груза; v — его макс. скорость.
В случае К. электрич. зарядов и токов в колебательном контуре или электрич. и магн. полей в эл.-магн. волнах роль потенциальной играет электрическая энергия, а кинетической — магнитная.
По мере изучения К. разл. физ. природы возникло убеждение о возможности общего, «внепредметного», подхода к ним, основанного на св-вах и закономерностях колебат. процессов
вообще. В результате появилась теория К. и волн. Осн. матем. аппаратом теории К. первоначально служили дифф. ур-ния в обыкновенных производных. Однако со временем изучаемые ею модели по существу распространились на все виды описаний динамич. систем: от интегродифференциально разностных до статистических (подробнее см. Колебаний и волн теория).
Кинематика К. позволяет выделить несколько наиб. типичных примеров (рис. 2). Для простоты будем говорить о К., описываемых ф-цией времени u(t), хотя с кинематич. точки зрения пространств. и временные К. взаимно сводятся друг к другу путём перехода из одной системы отсчёта к другой.
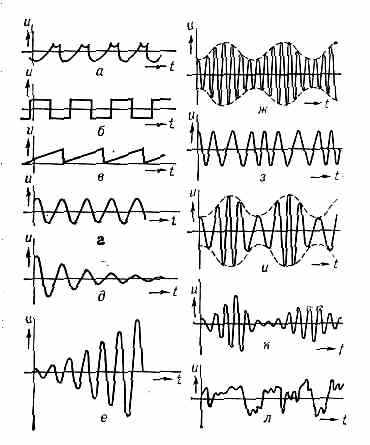
Рис. 2. Разл. виды колебаний: а — периодич. колебания сложной формы; б — прямоуг. колебания; в — пилообразные; г — синусоидальные; д — затухающие; е — нарастающие; ж — амплитудно-модулированные; в — частотно-модулированные; и — колебания, модулированные по амплитуде и по фазе; к — колебания, амплитуда и фаза к-рых — случайные ф-ции; л — случайные колебания; u — колеблющаяся величина; t — время.
На рис. 2, а— г показаны периодич. К. разл. формы, в к-рых любое значение u(t) повторяется через одинаковые промежутки времени Т, наз. периодом К., т. е. u(t+T)=u(t). Величину, обратную периоду Т и равную числу К. в ед. времени, наз. частотой К. =1/T; пользуются также круговой или циклич. частотой =2. В случае пространств. К. вводят аналогичные понятия пространств. периода (или длины волны Я) и волн. числа k=2/.
Разновидностями периодич. К. явл. прямоугольные (рис. 2, б), пилообразные (рис. 2, в) и наиб. важные синусоидальные, или гармонические
293
колебания (рис. 2, г). Последние могут быть записаны в виде:
u(t)=asin=asin(t+0),
где а — амплитуда, — фаза, 0 — её нач. значение. В случае строго гармонич. К. величины а, и 0 не зависят от времени. Часто употребляется также комплексная запись синусоидальных К.
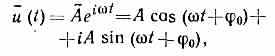
к-рая удобна при расчётах, однако физ. смысл имеют отдельно вещественная и мнимая части. При этом комплексная амплитуда ААеi0 объединяет в себе действит. значения амплитуды и фазы К. Для показанного на рис. 2, д затухающего К.
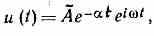
где коэфф. затухания а можно относить либо к мнимой части комплексной частоты +i, либо к экспоненциально убывающей амплитуде. Иногда вводят понятие декремента затухания =Т; при отрицательных б этот коэфф. наз. инкрементом, амплитуда соответствующего К. экспоненциально нарастает. У К. с перем. амплитудой периодичность нарушается; но при << их всё же можно считать почти (квази) периодическими, а при >> — почти апериодическими, т. е. по существу уже не К., а монотонными процессами. Для передачи информации применяются модулиров. К. (рис. 2, ж—и), амплитуда, фаза или частота к-рых изменяются по определ. закону в соответствии с передаваемыми сигналами, напр. в радиовещании ВЧ К. модулируются К. звук. частот, передающими речь, музыку (см. Модуляция колебании).
При изучении стохастич. процессов приходится иметь дело с частично и полностью случайными К. На рис. 2, к показан пример синусоидального К., модулированного по амплитуде и фазе случайными ф-циями, а на рис. 2, л дана одна из реализаций совершенно неупорядоченного процесса («белого шума»), к-рый лишь условно можно отнести к К.
Колебат. движения на плоскости и в пр-ве в принципе могут быть представлены как совокупность одномерных К. вдоль соответствующих осей координат. Так, два гармонич. К. (одномерные осцилляторы) с частотами n (вдоль оси х) и m (вдоль оси ух) (при рациональном отношении п/т) явл. проекциями сложных периодических плоских К., наз. Лиссажу фигурами. Равномерное движение по окружности (ротатор) можно разложить на два одинаковых гармонич. К. (n=m), сдвинутых по фазе на /2. В природе и во мн. техн. устройствах часто возникают движения,
почти не отличающиеся (на протяжении больших промежутков времени) от чисто гармонических или равномерно вращательных. Мн. физ. приборы (спектр. анализаторы) выделяют из произвольных процессов наборы К., близких к гармоническим. Возможна и обратная процедура синтеза гармонич. К., математически соответствующая рядам и интегралам Фурье, в силу к-рой любой временной процесс можно воссоздать сложением или интегрированием гармонич. К. разл. частот и амплитуд.
Динамика К. Свободные, или собственные, К. явл. движением системы, предоставленной самой себе, в отсутствии внеш. воздействий. При малых отклонениях от состояния равновесия движения системы удовлетворяют суперпозиции принципу, согласно к-рому сумма двух произвольных движений также составляет допустимое движение системы; такие движения описываются линейными ур-ниями (в частности, дифференциальными). Если система ещё и консервативна (т. е. в ней нет потерь или притока энергии извне), а её параметры не изменяются во времени (о переменных параметрах будет сказано ниже), то любое собств. К. может быть однозначно представлено как сумма нормальных колебаний, синусоидально изменяющихся во времени с определёнными собств. частотами. В колебат. системах с сосредоточенными параметрами, состоящих из N связанных осцилляторов (напр., цепочка из колебат. электрич. контуров или из соединённых упругими пружинками шариков), число норм. колебаний (мод) равно N. В системах с распределёнными параметрами (струна, мембрана, полый или открытый резонатор) таких К. существует бесконечное множество. Напр., для струны длиной L с закреплёнными концами моды отличаются числом полуволн, к-рые можно уложить на всей длине струны: L=n/2(n=0, 1, 2, . . ., ). Если скорость распространения волн вдоль струны равна v, то спектр собств. частот определяется ф-лой: n=knv=2/Tn=2v/n=nv/L (n=0, 1, 2, . . ., ). Наличие дисперсии, когда v=v(), искажает это простое эквидистантное распределение частот, спектр к-рых определяется уже из т. н. дисперсионного ур-ния: n=(kn)=(n/L)v(n). В реальных системах собств. К. будут затухать из-за потерь, поэтому их можно считать приближённо гармоническими лишь в интервале времени, меньшем 1/. Затухающее К. (рис. 2, д) можно представить в виде пакета гармонич. К., непрерывно заполняющих интервал частот (0:±), тем более узкого, чем меньше , т. к. ~. В этом случае говорят об уширении спектр. линии. Т. о., сгущение спектра из-за дисперсии и уширение линии из-за потерь может повлечь за собой превращение дискр. спектра в сплошной (ширина линий становится прибл. равной интервалу между ними, т. е ~~(n+1-n).
Наличие даже слабой нелинейности систем с дискр. спектром собств. частот приводит к «перекачке» энергии К. по спектр. компонентам; при этом возникают процессы «конкуренции мод» — выживание одних и подавление других. Дисперсия может стабилизировать эти процессы и привести к формированию устойчивых пространственно-временных образований, примерами к-рых в системах с непрерывным спектром явл. солитоны.
Возбуждение К. происходит: либо путём непосредств. воздействия на колебат. систему (раскачка маятника периодич. толчками, включение периодической эдс в колебат. контур и т. д.) — в этом случае говорят о вынужденных колебаниях; либо путём периодич. изменения параметров колебат. системы (длины подвеса маятника, ёмкости или самоиндукции контура, коэфф. упругости струны и т. п.) — т. н. параметрич. возбуждение колебаний; либо благодаря развитию неустойчивостей и возникновению самосогласованных колебат. движений внутри самой системы — т. н. автоколебания.
Особое значение при возбуждении К. имеет явление резонанса, состоящее в резком увеличении амплитуды К. при приближении частоты внеш. воздействия к нек-рой резонансной частоте, характеризующей систему. Если последняя линейна и параметры её не зависят от времени, то резонансные частоты совпадают с частотами её собств. К. и соответствующий отклик тем сильнее, чем выше добротность К. Раскачка происходит до тех пор, пока энергия, вносимая извне (напр., при каждом отклонении маятника), превышает потери за период осцилляции. Для линейных К. энергия, получаемая от источника, пропорц. первой степени амплитуды, а потери растут пропорц. её квадрату, поэтому баланс энергий всегда достижим.
При больших амплитудах К. становятся нелинейными, происходит смещение собств. частот системы и обогащение их спектра гармониками и субгармониками. Ограничение амплитуды колебаний может быть обусловлено как нелинейной диссипацией энергии, так и уходом системы из резонанса. При возбуждении К. в системах с распределёнными параметрами макс. амплитуды достигаются в случае пространственно-временного резонанса, когда не только частота внеш. воздействия, но и его распределение по координатам хорошо «подогнаны» к структуре норм. моды или, на языке бегущих волн, когда наступает совмещение не только их частот (резонанс), но и волн. векторов (синхронизм) .
Существует нек-рый выделенный класс вынужденных К., при к-ром
294
внеш. воздействие, не являясь чисто колебательным (напр., мгновенный удар), имеет, однако, настолько богатый частотный спектр, что в нём всегда содержатся резонансные частоты системы. Напр., заряж. ч-ца, пролетающая между двумя металлич. плоскостями, возбуждает почти весь набор нормальных эл.-магн. К. и волн, свойственный этой системе. Сюда же следует отнести черенковское излучение (см. Черенкоеа — Вавилова излучение) или тормозное излучение ч-цы в однородных средах, когда и спектр внеш. воздействия и спектр собственных К.— оба сплошные, т. е. в них представлены все возможные частоты. Наконец, есть и совсем аномальный случай вынужденных К. в системах с непрерывным спектром собств. частот типа ротатора (маховик, колесо, эл-н в магн. поле и т. п.), где вращат. движение (а следовательно, и два ортогональных колебат. движения) может возбуждаться силами, неизменными во времени.
Параметрич. возбуждение К. возникает при периодич. воздействии на те параметры системы, к-рые определяют величину запасённой колебат. энергии: в электрич. контуре — это индуктивность или ёмкость (но не сопротивление), у маятника — это длина нити или масса груза (но не коэфф. трения). См. Параметрический резонанс, Параметрическая генерация и усиление электромагнитных колебаний.
При определ. условиях в такой нелинейной колебат. системе могут возникать непрекращающиеся самоподдерживающиеся К., или автоколебания, при к-рых внеш. источнику отводится лишь ф-ция восполнения потерь энергии на диссипацию. Процесс формирования автоколебаний обычно состоит в последовательном самосогласовании движений. Пусть нач. состояние системы неустойчиво либо по отношению к ничтожно малым флуктуациям (мягкий режим возбуждения), либо по отношению к определ. конечным возмущениям (жёсткий режим возбуждения). В любом случае спонтанно (случайно) возникшее К. начнёт увеличиваться по амплитуде (процесс усиления К.), эти усиленные К. через элемент положительной обратной связи, обеспечивающий самосогласованность фаз, снова «подаются» в место своего возникновения и снова усиливаются и т. д. Получается очень быстрый (чаще всего экспоненциальный) рост К. Ограничение К. наступает из-за конечности энергетич. ресурсов, а также из-за рассогласованности фаз (подробнее см. А втоколебания).
К. могут быть самого широкого диапазона частот v и периодов Т. Так, приведём для примера значения Т или v для нек-рых важнейших К. и вращений: теор. модель пульсации Вселенной (T~1017—1018 с); обращение Солнца вокруг центра Галактики
(T~1016 с); ледниковые периоды на Земле (7'~1011—1012 с); наибольший цикл солн. активности (T~7•108 с); обращение Земли вокруг Солнца — год (T~3•107 с); обращение Луны вокруг Земли — лунный месяц (Т~2,4•106 с); вращение Земли вокруг своей оси — сутки (T~9•104 с); оборот часовой стрелки (T=4,3•104 с); оборот минутной стрелки (T=36•103с); ветровые волны на море (Т~1 с или ~l Гц); опасные для человека инфразвуки (=5—10 Гц); колесо автомобиля при скорости 60 км/ч (~10 Гц); звук. волны, воспринимаемые человеком на слух (=20—2•104 Гц); стандартная частота К. перем. тока (=50 Гц); УЗ (=2•104—109 Гц); эл.-магнитного К. радиодиапазона (=105—3•108 Гц); эл.-магн. К. СВЧ диапазона (=3•108—3•1011); гиперзвук (=109—1013 Гц); типичные колебания атомов в молекуле (~1011—1013 Гц); оптика (видимый свет) (~0,4•1014—0,75•1014 Гц); УФ излучение (~1015—1017 Гц); рентг. изяучение (~1018—1019 Гц); гамма-лучи (~1020 Гц); короткоживущие частицы — резонансы (T=10-22—10-24 с).
• Стретт Дж. В. (лорд Рэлей), Теория звука, пер. с англ., 2 изд., т. 1—2, М., 1955; Андронов А. А., В и т т А. А., X а й к и н С. Э., Теория колебаний, 3 изд., М., 1981; Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Бишоп Р., Колебания, пер. с англ., 2 изд., М., 1979.
М. А. Миллер, М. И. Рабинович.
КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ, один из осн. видов внутр. движений тв. тела, когда составляющие его структурные ч-цы (атомы, ионы, молекулы) колеблются около положений равновесия — узлов кристаллической решётки. Амплитуда колебаний тем больше, чем выше темп-pa, но всегда существенно меньше, чем постоянная решётки. Когда амплитуда достигает нек-рого критич. значения, крист. структура разрушается, начинается процесс плавления. Наоборот, при понижении темп-ры амплитуда уменьшается. Однако полное прекращение колебаний запрещено законами квант. механики; при Т=0К атомы совершают нулевые колебания. Энергия нулевых колебаний мала, поэтому с понижением темп-ры все жидкости затвердевают, за исключением жидкого гелия, к-рый затвердевает при Т=0К только при повыш. давлении. На тепловые К. к. р. (фон) могут налагаться звук. колебания, вызванные распространением в кристалле упругих волн, порождаемых внешним воздействием (удар, периодическая внешняя сила).
Под колебаниями атомов и ионов подразумеваются колебания массивных по сравнению с эл-нами ат. ядер. Это позволяет приписать кристаллу потенц. энергию, зависящую только от координат ядер (адиабатическое приближение).
Силы, к-рые стремятся удержать атомы в положении равновесия, приближённо можно считать пропорциональными их относит. смещениям, как если бы атомы были связаны упругими «пружинками» (рис. 1). Представление кристалла в виде совокупности ч-ц, связанных упругими силами, наз. гармоническим приближением. В такой системе могут распространяться упругие волны разной длины. При
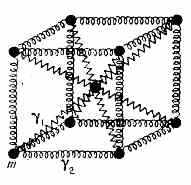
Рис. 1. Представление объёмно-центрированного кубич. кристалла в виде совокупности ч-ц массы m, связанных друг с другом «пружинками» с жёсткостью .
, больших, чем межатомные расстояния (малые частоты колебаний), гармонич. приближение даёт те же результаты, что и модель кристалла как сплошной упругой среды. Для больших частот, когда длина волны сопоставима с межат. расстояниями, начинает сказываться дискр. ат. структура кристалла, при низких темп-pax проявляются квант. эффекты. Это было экспериментально обнаружено по отклонению теплоёмкости от Дюлонга и Пти закона и объяснено в теории Эйнштейна (модель кристалла как совокупности гармонич. осцилляторов, колеблющихся с одинаковой частотой) и более строго в теории Дебая, где был учтён непрерывный спектр частот осцилляторов.
Оказалось, что имеется глубокая аналогия между светом и упругими волнами в кристаллах; для последних также имеет место дискретность энергии. Кванты энергии упругих колебаний были названы фононами. Энергия фонона равна ђ ( — частота колебаний). Звук. волны в кристаллах рассматриваются как распространение квазичастиц фононов, тепловые К. к. р.— как термич. возбуждение фононов.
Можно показать, что в кристалле, состоящем из N элементарных ячеек по v атомов в каждой, существуют 3N-6 типов простейших колебаний, наз. нормальными колебаниями или модами. Их число равно числу степеней свободы у совокупности частиц, составляющих кристалл, за вычетом трёх степеней свободы, отвечающих поступательному, и трёх — вращательному движению кристалла как целого (см. Степеней свободы число). Числом 6 можно пренебречь, т. к. 3vN — величина ~1022— 1023 для 1 см3 кристалла. В кристалле одновременно могут существовать все возможные нормальные колебания, причём каждое протекает так, как если бы остальных не было вовсе. Любое движение атомов в кристалле,
295
не нарушающее его микроструктуры, представляется в виде суперпозиции норм. колебаний кристалла (см. Суперпозиции принцип).
Каждое норм. колебание можно представить в виде двух упругих плоских бегущих волн, распространяющихся в противоположных направлениях (н о р м а л ь н ы е в о л н ы).
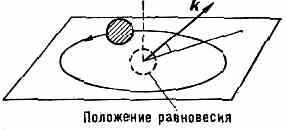
Рис. 2. Эллиптич. поляризация упругих волн в кристалле; k — волн. вектор.
Плоская бегущая волна, помимо частоты , характеризуется волн. вектором k, а также нек-рым числом , к-рое определяет тип и поляризацию волны, т. е. направление смещения отд. атомов. В общем случае имеет место эллиптич. поляризация, когда каждый атом в данном норм. колебании описывает эллипс около своего положения равновесия (рис. 2). При этом нормаль к плоскости эллипса не совпадает по направлению с k. Эллиптич. орбиты одинаковы для идентичных атомов, занимающих эквивалентные положения в решётке. В тех кристаллах, где каждый узел явл. центром симметрии (см. Симметрия кристаллов), все норм. волны плоско поляризованы: атомы в любом норм. колебании совершают возвратно-поступат. движения около своих положений равновесия.
Упругие волны в кристалле всегда обладают дисперсией (см. Дисперсия волн). В частности, их фазовая скорость, как правило, отличается от групповой скорости, с к-рой по кристаллу переносится энергия колебаний. Т. к. вз-ствие между атомами конечно по величине, то в кристалле существует нек-рая макс. частота колебаний макс (обычно макс~1013 Гц). Частоты норм. колебаний могут не сплошь заполнять интервал от =0 до =макс, в нём могут быть пустые участки (запрещённые зоны). Колебания, частоты к-рых соответствуют запрещённым зонам, и колебания с частотами >макс не могут распространяться в кристалле. " Акустические и оптические ветви нормальных колебаний. Все 3N норм, колебаний объединяются в 3 групп или ветвей с разл. поляризациями по N колебаний в каждой, отличающихся значениями волн. вектора k. Для каждой ветви а (=1, 2, 3, ... 3) существует свой закон дисперсии =(k). Если представить кристалл в виде совокупности одинаковых атомов массы т, расположенных на равных расстояниях а друг от друга и связанных попарно «пружинками» с жёсткостью так, что они образуют бесконечную цепочку и могут смещаться только вдоль её оси (рис. 3, о), то элем. ячейка состоит из одной ч-цы и имеет только одну степень свободы.
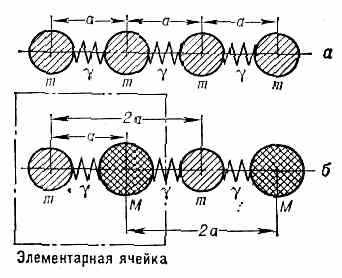
Рис. 3. Простейшие модели кристалла: а — линейная одноат. цепочка; б — линейная двухат. цепочка; m и М — массы двух ч-ц, составляющих элем. ячейку.
При этом существует только одна ветвь норм. колебаний с законом дисперсии:
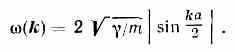
У двухат. линейной цепочки (рис. 3, б) ячейка содержит две ч-цы (=2) с массами m и М и имеются две ветви с более сложными законами дисперсии (рис. 4).
В трёхмерном кристалле всегда существуют три ветви колебаний =1, 2, 3, наз. акустическими, у к-рых при k=0 частоты =0. В случае, когда длина волны значительно превышает наибольший из периодов пространств. решётки (k— мало), акустич. ветви характеризуются линейным законом дисперсии =ck. Это обычные звук. волны (отсюда термин «акустич. ветвь»), а с — фазовая скорость их распространения, зависящая от направления распространения и поляризации. Они плоско поляризованы в одном из трёх взаимно перпендикулярных направлений, отвечающих трём значениям =1, 2, 3 и соответствующих колебаниям кристалла как сплошной среды. В анизотропном кристалле ни одно из этих направлений обычно не совпадает с направлением распространения волны, т. е. с k. Лишь в упруго-изотропной среде звук. волны имеют чисто продольную и чисто поперечную поляризации. Акустич. ветви охватывают диапазон частот от =0 до ~1013 Гц. С уменьшением закон дисперсии становится более сложным.
Для остальных 3 (-1) ветвей смещения атомов в процессе колебаний, соответствующих большой длине волны, происходят так, что центр масс отдельной элем. ячейки покоится (при k0 атомы движутся.«навстречу» друг другу). В ионных кристаллах движение такого типа можно возбудить переменным электрич. полем, напр.
световой волной с частотой, лежащей в ИК области. Поэтому эти ветви наз. оптическими. Спектр колебаний одноат. цепочки содержит одну акустич. ветвь. В случае двухат. цепочки имеются две ветви — одна акустическая и одна оптическая (рис. 4).

Рис. 4. Закон дисперсии частот двухат. линейной цепочки: 1— акустич. ветвь; 2 — оптич. ветвь.
