От лат cavitas пустота), образование в капельной жидкости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац
| Вид материала | Документы |
- Вывихи. Переломы, 241.71kb.
- От лат evaporo испаряю и греч grapho пишу), метод получения изображений объектов, 2696.94kb.
- Реферат от лат rеfеrо "сообщаю", 198.27kb.
- Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
- Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
- Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
- Реферат от лат. «сообщать», 61.18kb.
- Лекция. Взаимосвязанные рынки, 285.49kb.
- Реферат Реферат, 36.91kb.
- Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.
Т. к. период крист. решётки (~10 Å) во много раз меньше длинны волны видимого света (4000—7000 Å), кристалл можно рассматривать как однородную, но анизотропную среду. Оптическая
анизотропия кристаллов обусловлена анизотропией поля сил вз-ствия ч-ц. Хар-р этого поля связан с симметрией кристаллов. Все кристаллы, кроме кубических, оптически анизотропны.
В изотропных средах вектор электрич. индукции D связан с вектором электрич. поля Е соотношением: D=Е, где диэлектрич. проницаемость — скалярная величина, в случае перем. полей зависящая от их частоты (см. Диэлектрики). Т. о., в изотропных средах векторы D и Е имеют одинаковое направление. В кристаллах направления векторов D и Е не совпадают, а соотношение между этими величинами имеет более сложный вид, т. к. диэлектрич. проницаемость , описываемая тензором, зависит от направления в кристалле (см. Пространственная дисперсии). Следствием этого и явл. анизотропия оптич. св-в кристаллов, в частности зависимость скорости распространения в нём волны v и преломления показателя n от направления.
Если из произвольной точки О кристалла провести по всем направлениям радиусы-векторы r, модули к-рых r=n=, где — диэлектрич. проницаемость в направлении r при данной частоте колебаний, то концы векторов r будут лежать на
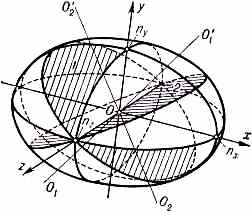
Рис. 1. Оптич. индикатриса двуосного кристалла — трёхосный эллипсоид; его оси симметрии Ох, Оу и Oz наз. гл. осями индикатрисы; nх, ny, nz — показатели преломления вдоль гл. осей; 1 и 2 — два круговых сечения эллипсоида; O1 O' и О2 О2' — оптич. оси кристалла.
поверхности эллипсоида, наз. оптической индикатрисой (рис. 1). Оси симметрии этого эллипсоида определяют три взаимно перпендикулярных главных направления в кристалле, по к-рым направления векторов D и E совпадают. В прямоуг. декартовой системе координат, осп к-рой совпадают с гл. направлениями, ур-ние оптич. индикатрисы имеет вид:

где nх, ny и nz— значения n вдоль гл. направлений (гл. значения n), Оптической осью кристалла наз. нормаль N к плоскости кругового сечения оптич. индикатрисы.
Для кубнч. кристаллов оптич. индикатриса превращается в сферу с ра-
324
диусом r=n. В кристаллах ср. сингоний (тригональной, тетрагональной и гексагональной) одно из гл. направлений совпадает с гл. осью симметрии кристалла. В этих кристаллах
оптич. индикатриса — эллипсоид вращения, и они имеют только одну оптич. ось, совпадающую с осью вращения эллипсоида. Такие кристаллы наз. дноосными. Кристаллы низших сингоний (ромбической. моноклинной и триклинной) наз. двуосными. Их оптич. индикатриса — трёхосный эллипсоид, имеющий два круговых сечения и две оптич. оси (рис.. 1).
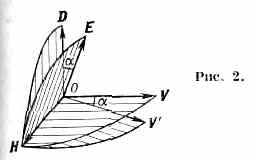
Вследствие несовпадения направлений векторов D и E поляризованная плоская монохроматич. волна в кристалле характеризуется двумя тройками взаимно перпендикулярных векторов D, H, v и Е, Н, v' (рис. 2). Скорость v' совпадает по направлению с Пойнтинга вектором S и равна скорости переноса энергии волной. Её называют лучевой скоростью волны. Скорость v наз. нормальной скоростью волны. Она равна скорости распространения фазы и фронта волны по направлению нормали N к фронту. Величины v и v' связаны соотношением: v'=v/cos, где — угол между векторами D и Е.
Нормальная и лучевая скорости волны определяются из уравнения Френеля — осн. ур-ния К., к-рое имеет вид:
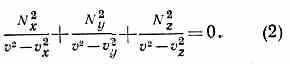
Здесь Nx, Ny и Nz — проекции вектора нормали N на гл. направления кристалла; vx=c/nx, vy=clny, vz=c!nz — гл. фазовые скорости волны.
Т. к. ур-ние Френеля — квадратное относительно v, то в любом направлении N имеются два значения нормальной скорости волны v1 и v2, совпадающие только в направлении оптич. осей кристаллов. Если из точки О откладывать по всем направлениям N векторы соответствующих им нормальных скоростей v1 и v2, то концы векторов будут лежать на двух поверхностях, наз. поверхностями нормалей. У одноосного кристалла одна из поверхностей — сфера, вторая— овалоид, к-рый касается сферы в двух точках пересечения её с оптич. осью. У двуосных кристаллов эти поверхности пересекаются в четырёх точках, лежащих на двух оптич. осях (б и н о р м а л я х).
Аналогично геом. место точек, удалённых от точки О на расстояния
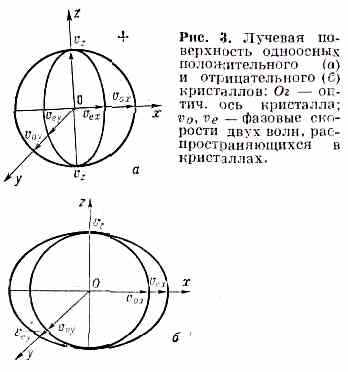
v1 и v2, наз. лучевыми поверхностями или поверхностями волны. В одноосных кристаллах одна из поверхностей — сфера, вторая — эллипсоид вращения вокруг оптич. оси Oz. Сфера и эллипсоид касаются друг друга в точках их пересечения с оптич. осью (рис. 3). В двуосных кристаллах поверхности пересекаются друг с другом в четырёх точках, попарно лежащих на двух прямых, пересекающихся в точке О (б и р а д и а л и).
Т.о., в кристаллах в произвольном направлении N могут распространяться две плоские волны, поляризованные в двух взаимно перпендикулярных плоскостях.
Направления векторов D1 и D2 этих волн совпадают с осями эллипса, получающегося при пересечении оптич. индикатрисы с плоскостью, перпендикулярной N и проходящей через точку О. Нормальные скорости этих волн равны: v1=с/n1 и v2=с/n2. Векторы E1 и Е2 этих волн также лежат в двух взаимно перпендикулярных плоскостях, причём им соответствуют два лучевых вектора S1 и S2 и два значения лучевой скорости v'1= v1/cos и v'2=v2/cos.
При преломлении света на границе кристалла в нём возникают два преломлённых луча, один из к-рых подчиняется обычным законам преломления и поэтому наз. обыкновенным (о), а второй не подчиняется этим законам и наз. необыкновенным (е) (см. Двойное лучепреломление). Одноосный кристалл наз. положительным, если v0>ve, и отрицательным, если v0
Две световые волны с ортогональной поляризацией, распространяющиеся внутри кристалла в одном направлении, приобретают за счёт различия показателей преломления разность хода. С помощью поляризац. устройства можно свести направления колебаний в вышедших из кристалла волнах в одну плоскость и наблюдать их
интерференцию (см. Интерференция поляризованных лучей).
В кристаллах нек-рых классов симметрии вдоль каждого направления могут распространяться две эллиптически поляризованные волны (с противоположными направлениями обхода) — обе со своим показателем преломления. В направлении оптич. оси поляризация волн оказывается круговой, что приводит к вращению плоскости поляризации падающего на кристалл линейно поляризованного света.
В сильно поглощающих кристаллах линейно поляризованная волна расщепляется на две эллиптически поляризованные волны с одинаковым направлением обхода. В таких кристаллах наблюдается разл. поглощение волн, обладающих разной поляризацией.
Каждый кристалл обладает присущим ему комплексом кристаллооптич. св-в и величин, по к-рым он может быть идентифицирован. В прикладной К. разработаны разл. методы измерения этих величин (иммерсионный метод, коноскопия и др.).
Методы К. используют для получения и анализа поляризованного света, для создания оптических затворов, модуляторов, дефлекторов и др.
• Б о р н М., В о л ь ф Э., Основы оптики, пер. с англ., М., 1973; Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Федоров Ф. И., Оптика анизотропных сред, Минск, 1958; Шубников А. В., Основы оптической кристаллографии, М., 1958; Татарский В. В., Кристаллооптика и иммерсионный метод исследования минералов, М., 1965; Дитчберн Р., Физическая оптика, пер. с англ., М., 1965; С т о й б е р Р., Морзе С., Определение кристаллов под микроскопом, пер. с англ., М., 1974; Современная кристаллография, т. 4, М., 1981, гл. 8.
В. В. Татарский, Б. Н. Гречушников.
КРИСТАЛЛОФИЗИКА, изучает физ. св-ва кристаллов и др. анизотропных сред, влияние разл. внеш. воздействий на эти св-ва и реальную структуру кристаллов. В отношении мн. физ. св-в дискретность решётчатого строения кристалла не проявляется, и кристалл можно рассматривать как сплошную однородную анизотропную среду. Понятие однородности среды означает рассмотрение физ. явлений в объёмах, значительно превышающих объём элем. ячейки кристалла. Св-ва кристаллов зависят от направления (анизотропия), но одинаковы в направлениях, эквивалентных по симметрии (см. Симметрия кристаллов).
Для количеств. описания физ. св-в кристаллов в К. используется матем. аппарат матричного и тензорного исчисления и теории групп. Нек-рые св-ва кристаллов, напр. плотность, не зависят от направления и характеризуются скалярными величинами. Фнз. св-ва, характеризующие взаимосвязь между двумя векторными величинами (напр., между поляриза-
325
цией P и электрич. полем Е, плотностью тока j и электрич. полем Е) или псевдовекторными величинами (напр., между магн. индукцией В и напряжённостью магн. поля Н), описываются тензорами второго ранга (напр., тензоры диэлектрической восприимчивости, электропроводности, магнитной проницаемости). Многие физические поля в кристаллах, напр. электрич. и магн. поля, поле механич. напряжений, сами явл. тензорными (векторными) полями. Связь между физ. полями и св-вами кристаллов или между их св-вами может описываться тензорами высших рангов, характеризующими такие св-ва, как пьезоэлектрич. эффект (см. Пьезоэлектричество), электрострикция, магнитострикция, упругость, фотоупругость и т. д.
Диэлектрич., магн., упругие и др. св-ва кристаллов удобно представлять в виде т. н. указательных поверхностей. Описывающий такую поверхность радиус-вектор характеризует величину той или иной кристаллофиз. константы для данного направления (см. Индикатриса в оптике). Симметрия любого св-ва кристалла не может быть ниже симметрии его внеш. формы (п р и н ц и п Н е й м а н а). Иными словами, группа симметрии g1, описывающая любое физ. св-во кристалла, неизбежно включает элементы симметрии его точечной группы G, т. е. является её надгруппой: G1∩G. Так, кристаллы, обладающие центром симметрии, не могут обладать полярными св-вами, т. е. такими, к-рые изменяются при изменении направления на обратное, напр. пироэлектрическими (см. Пироэлектрики). Наличие элементов симметрии определяет ориентацию гл. осей указательной поверхности и число компонент тензоров, описывающих то или иное физ. св-во. Так, в кристаллах кубич. сингонии все физические св-ва, описываемые тензорами второго ранга, не зависят от направления. Такие кристаллы изотропны относительно этих св-в (указательная поверхность — сфера). Те же св-ва в кристаллах ср. сингонии (тетрагональной, тригональной и гексагональной) характеризуются симметрией эллипсоида вращения, т. е. тензор 2-го ранга имеет две независимые компоненты. Одна из них описывает св-во вдоль гл. оси кристалла, а другая — в любом из направлений, перпендикулярных гл. оси. Для полного описания св-в таких кристаллов в любом направлении только эти две величины и необходимо измерить. В кристаллах низших сингонии физические св-ва, описываемые тензорами второго ранга, обладают симметрией трёхосного эллипсоида и характеризуются тремя гл. значениями (и ориентацией гл. осей этого тензора).
Физ. св-ва, описываемые тензорами более высокого ранга, характеризуются большим числом параметров. Так, упругие св-ва, описываемые тензором 4-го ранга, для кубич. кристалла характеризуются тремя, а для изотропного тела двумя независимыми величинами. Для описания упругих св-в триклинного кристалла необходимо определить 21 независимую компоненту тензора. Число независимых компонент тензоров высших рангов (5-го, 6-го и т. д.) для разных точечных групп симметрии определяется методами теории групп. Полное определение физ. св-в кристаллов и текстур осуществляется радиотехн., акустич., оптич. и др. методами.
В К. исследуются как явления, характерные только для анизотропных сред (двойное лучепреломление, вращение плоскости поляризации света, прямой и обратный пьезоэффекты, электрооптич., магнитооптич. и пьезооптич. эффекты, генерация оптич. гармоник и др.), так и явления, наблюдаемые и в изотропных средах (электропроводность, упругость и т. д.). Последние в кристаллах могут иметь особенности, обусловленные анизотропией.
К. явл. частью кристаллографии и примыкает к физике твёрдого тела и кристаллохимии; задачей К. явл. также исследование изменений св-в кристалла при изменении его структуры или сил вз-ствия в крист. решётке. Мн. задачи К. связаны с изменением симметрии кристаллов в разл. термодинамич. условиях. Кюри принцип позволяет предсказать изменение точечной и пространств. групп симметрии кристаллов, испытывающих фазовые переходы, напр., в ферромагн. и сегнетоэлектрич. состояния (см. Ферромагнетизм, Сегнетоэлектрики).
В К. изучаются и различного рода дефекты крист. решётки (центры окраски, вакансии, дислокации, дефекты упаковки, границы крист. блоков, зёрен, домены и т. д.) и их влияние на физ. св-ва кристаллов (на пластичность, прочность, электропроводность, люминесценцию, механич. добротность и т. д.). К задачам К. относится также поиск новых перспективных крист. материалов.
• Н а й Дж., Физические свойства кристаллов и их описание при помощи тензоров и матриц, пер. с англ., М., 1967. См. также лит. при ст. Кристаллография, Симметрия
кристаллов.
К. С. Александров.
КРИСТАЛЛОФОСФОРЫ (от кристаллы и греч. phos — свет, phoros — несущий), неорганич. крист. люминофоры. Люминесцируют под действием света, потока эл-нов, проникающей радиации, электрич. тока и т. д. К. могут быть только ПП и диэлектрики, в к-рых имеются центры люминесценции, образованные активаторами или дефектами крист. решётки (вакансиями, междоузельными атомами и др.). Механизм свечения К. в осн. рекомбинационный (см. Люминесценция).
Люминесценция К. может происходить как в результате возбуждения непосредственно центров люминесценции, так и при поглощении энергии возбуждения крист. решёткой К. и передаче её центрам люминесценции. Непосредств. рекомбинация эл-нов и дырок в К. также сопровождается свечением (краевая люминесценция). Длительность послесвечения К. от 10-9 с до неск. часов.
Основой К. служат сульфиды, селениды и теллуриды Zn и Cd, оксиды Са и Mn, галогениды щелочных металлов и нек-рые др. соединения, активаторами — ионы металлов (Cu, Со, Mn, Ag, Eu, Tu и др.). Синтез осуществляется чаще всего прокаливанием тв. шихты, нек-рые К. получают из газовой фазы или расплава. Комбинируя активаторы и основы, синтезируют К. для преобразования разл. видов энергии в видимый свет определ. длины волны с кпд до десятков %. К. обладают ярким свечением, хим. и радиац. стойкостью; применяются в люминесцентных лампах, экранах телевизоров и осциллографов, электролюминесцентных панелях, сцинтилляционных счётчиках, в кач-ве активной среды ПП лазеров и т. д.
• Фок М. В., Введение в кинетику люминесценции кристаллофосфоров, М., 1964; Физика и химия соединений АII, ВVI, пер. с англ., М., 1970.
Э. А. Сеириденков.
КРИСТАЛЛОХИМИЯ, раздел кристаллографии, в к-ром изучаются закономерности расположения атомов в кристаллах и природа хим. связи между ними. К. основана на обобщении результатов экспериментальных рентгенографич. и др. дифракц. методов исследований ат. структуры кристаллов (см. Рентгеновский структурный анализ, Электронография, Нейтронография), на классич. и квант. теориях хим. связи, на расчётах энергии крист. структур с учётом симметрии кристаллов. Кристаллохим. закономерности позволяют объяснить и в ряде случаев предсказать, исходя из хим. состава в-ва, расположение атомов или молекул в кристаллической решётке и расстояния между ними. Хим. связь между атомами в кристаллах возникает за счёт вз-ствия внеш. валентных электронов атомов. Равновесное расстояние между атомами обычно составляет 1,5—4 Å (в зависимости от типа хим. связи). При сближении атомов на расстояния, меньшие, чем равновесное, возникает резкое их отталкивание. Это позволяет в первом приближении приписать атомам для того или иного типа связи определ. «размеры», т. е. нек-рые пост. радиусы, и тем самым перейти от физ. модели кристалла как атомно-электронной системы к его геом. модели как системе несжимающихся шариков. Полное кристаллохим. описание ат. структуры того или иного кристалла включает указание размеров элем. ячейки, пространств. группы симметрии кристалла, коор-
326
динат атомов, расстоянии между ними, типа хим. связи; описания окружения атомов, характерных ат. группировок, тепловых колебаний атомов и т. п. По хар-ру хим. связи кристаллы делят на четыре осн. группы — ионные кристаллы (напр., NaCl), ковалентные (напр., алмаз, кремний), металлические (металлы и интерметаллич. соединения) и молекулярные кристаллы (напр., нафталин). В ионных кристаллах эл-ны переходят от атомов металлов, к-рые становятся положит.
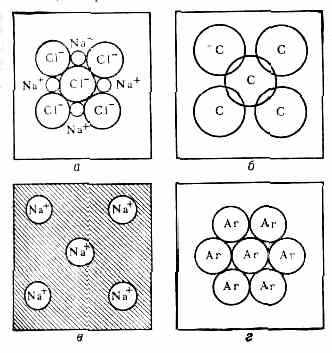
Осн. типы хим. связи в кристаллах: а — ионная связь; б — ковалентная связь; в — металлич. связь; г — связь за счёт сил Ван-дер-Ваальса.
ионами (катионами), к атомам неметаллов, к-рые становятся отрицат. ионами (анионами), что приводит к электростатич. притяжению между ними (рис., а). В случае ковалентной связи валентные эл-ны соседних атомов обобществляются, образуя «мостики» электронной плотности между связанными атомами (рис., б). В металлич. кристаллах валентные эл-ны образуют общий электронный «газ», осуществляющий коллективное вз-ствие атомов кристалла (рис., в). Расстояния между атомами для этих трёх типов связи составляют 1,5—2,5 Å. В мол. кристаллах атомы внутри молекул объединены прочными ковалентными связями, а атомы соседних молекул взаимодействуют за счёт более слабых ван-дер-ваальсовых сил, (рис., г), имеющих диполь-дипольное и дисперсионное происхождение (см. Межмолекулярное взаимодействие). Расстояние между атомами соседних молекул 3,5—4 Å. Во многих кристаллах связь имеет промежуточный хар-р, напр. в кристаллах полупроводников (Ge, GaAs) связь в осн. ковалентная, но с примесью ионной и металлической. В нек-рых кристаллах (напр., лёд, органич. кристаллы) существует т. н. водородная связь (см. Межатомное взаимодействие).
Каждому крист. в-ву присуща определ. структура, но при изменении тсрмодинамич. условий она иногда может меняться (полиморфизм). Обычно чем проще ф-ла соединения, тем более симметрична его структура. Кристаллы с одинаковой хим. ф-лой (в смысле числа и соотношения разл. атомов) могут иметь одинаковую крист. структуру (говорят, что они образуют данный «структурный тип») несмотря на различие типов связи (и з о с т р у к т у р н о с т ь): изоструктурны галогениды щелочных металлов типа NaCl и нек-рые окислы (напр., MgO), ряд сплавов (напр., Ti— Ni). Есть большие серии изоструктурных соединений с ф-лой вида АВ2, АВ3, АВХ3 и т. п. Изоструктурны кристаллы мн. элементов, напр. -Fe и Cu, образующие гранецентрированную кубич. решётку, но такую же структуру имеют и отвердевшие инертные газы. Если кристаллы изоструктурны и обладают одинаковым типом связи, то их называют изоморфными (см. Изоморфизм). Во многих случаях между изоморфными кристаллами возможно образование непрерывного ряда твёрдых растворов.
В геом. модели кристалла К. использует концепцию эфф. радиусов атомов, ионов и молекул (к р и с т а л л о х и м и ч е с к и е р а д и у сы). На основе эксперим. данных о расстояниях между атомами в кристаллах построены таблицы кристаллохим. радиусов для всех типов связей, так что межат. расстояние равно сумме радиусов (св-во аддитивности кристаллохим. радиусов). Молекулы в органич. кристаллах предстают как бы окаймлённые «шубой» ван-дер-ваальсовых радиусов.
Осн. геом. представлением в К. явл. теория плотной упаковки, к-рая наглядно объясняет расположение атомов в ряде металлич. и ионных структур. В последнем случае используется представление о заселении «пустот» в упаковке анионов катионами, имеющими меньший ионный радиус.
В мол. кристаллах структурной ед. плотной упаковки явл. молекула. К. органич. соединений рассматривает правила плотной упаковки молекул, связь симметрии молекул и симметрии кристалла, типы органич. структур. Особые кристаллохнм. закономерности выявляются в структуре полимеров, жидких кристаллов, биологических кристаллов.
Координац. число К и вид координац. многогранника характеризуют хим. связь данного атома и структуры кристалла в целом. Напр., Be (за редкими исключениями) и Ge имеют тетраэдрич. окружение (K=4), у Аl и Cr координац. многогранник — октаэдр, у Pd и Pt — квадрат (K=4). Малые координац. числа указывают на значит. роль направленной ковалентной связи, большие — на большую роль ионной или металлич. связей.
Во многих крист. структурах (графит, MoS2 и др.) сосуществуют связи разл. типов. Такие структуры наз. гетеродесмическими, в отличие от гомодесмических — с однотипной связью (алмаз, металлы,
NaCl, кристаллы инертных элементов). Для гетеродесмич. структур характерно наличие фрагментов, внутри к-рых атомы соединены более прочными (обычно ковалентнымп) связями. .Эти фрагменты могут представлять собой отд. «острова», цепи, слои, каркасы. Островные структуры типичны для мол. кристаллов. Часто в кач-ве «островов» выступают отд. молекулы и многоат. ионы (напр., SO-4, NO-3, СО-3) или ат. группировки типа РtСl6 в комплексных соединениях. Ряд кристаллов имеет цепочечное строение, типичный пример — кристаллы полимеров. Слоистую структуру имеют BN, MoS2, многие силикаты. Для нек-рых классов соединений характерно наличие устойчивых структурных группировок, сочетающихся в них по-разному. Так, в силикатах осн. структурный элемент — тетраэдрич. группировка SiO4 может выступать либо изолированной, либо образовывать пары, кольца, цепочки, слои и т. п.
Образование той или иной крист. структуры определяется общим принципом термодинамики: наиболее устойчива структура, к-рая при данном давлении и данной темп-ре Т имеет минимальную свободную энергию W= U-ST, где U — энергия связи кристалла (энергия, необходимая для разъединения кристалла на отд. атомы или молекулы) при T=0 К, S — энтропия.
Свободная энергия тем выше, чем сильнее связь в кристаллах. Она составляет 100—20 ккал/моль для кристаллов с ковалентной связью, несколько меньше у ионных и металлич. кристаллов и наиболее низка для мол. кристаллов с ван-дер-ваальсовыми связями (1—10 ккал/моль). Теоретич. определение свободной энергии и предсказание структуры пока возможны лишь для сравнительно простых случаев. Они проводятся в рамках зонной квантовой теории тв. тела. В ряде случаев достаточно точные результаты даёт использование полуэмпирич. выражений для потенц. энергии вз-ствия атомов в кристаллах с тем или иным типом связи.
• Б о к и й Г. Б., Кристаллохимия, 3 изд., ., 1971; Китайгородский А. И., Органическая кристаллохимия, М., 1955; Киттель Ч., Введение в физику твердого тела, пер. с англ., М., 1978; К р е б с Г., Основы кристаллохимии неорганических соединений, пер. с нем., М., 1971; П е н к а л я Т., Очерки кристаллохимии, пер. с польск., Л., 1974; Урусов В. С., Энергетическая кристаллохимия, М., 1975; Современная кристаллография, т. 2, М., 1979.
Б. К. Вайнштейн.
