От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Калориметр ионизацион­ный Н. Л. Григоров. В. Л. Соколов. Рис. 2. Рассеяние ч-ц на цепочке атомов:  — угол падения ч-цы на цепочку;  Ю. В. Мартыненко. Кандела на квадратный метр Канонический ансамбль гиббса Каноническое распределе­ние гиббса Капиллярная конденсация Капиллярное давление Капиллярные волны Капиллярные явления Рис. 1. Капиллярное поднятие жидкости, смачивающей стенки (вода в стеклянном со­суде и капилляре). Кель­вина уравнением Рис. 2. а — переме­щение жидкости в ка­пилляре под дейст­вием разности капил­лярных давлений (r Н. В. Чураев.

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КАЛОРИМЕТР ИОНИЗАЦИОН­НЫЙ, прибор для измерения энергии адронов (с энергией >10¹¹ эВ). Энергия ч-цы поглощается в толстом слое в-ва; ч-цы высоких энергий в результате ядерных реакций рождают большое число вторичных ч-ц, в частности фо­тонов, к-рые в свою очередь образуют новые ч-цы, и т. д. В конечном итоге образуется лавина ч-ц (электронно-фотонный ливень). Если толщина слоя поглощающего в-ва достаточно велика и лавина заряж. ч-ц полностью тор­мозится в нём, то число созданных в в-ве ионов пропорц. энергии первич­ной косм. ч-цы. Для измерения полного числа ионов поглотитель из плотного в-ва (обычно Fe или Pb) разбивается

на ряд слоев толщиной в неск. см, между к-рыми размещаются детекто­ры, напр. ионизационные камеры.

К. и. применяется для изучения вз-ствий косм. ч-ц высокой энергии (10¹¹—10¹³ эВ) с ат. ядрами и в эк­спериментах на ускорителях. Его обычно сочетают с приборами, поз­воляющими наблюдать результаты этого вз-ствия с ядерными фотографи­ческими эмульсиями (рис. ), с искровы­ми камерами и др.



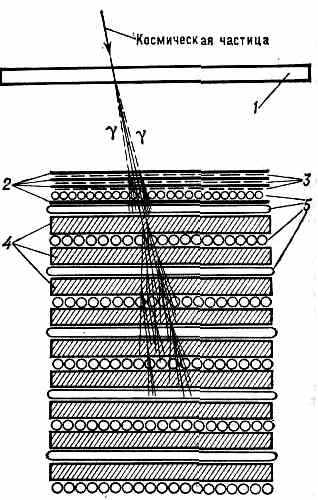
Рис. Схема ионизац. калориметра в сочета­нии с яд. фотоэмульсиями; 1 — мишень, в к-рой происходит вз-ствие косм. ч-цы с яд­рами атомов мишени, приводящее к появле­нию -квантов высоких энергий; 2 — слои Pb, в к-рых -излучение порождает мощные лавины заряж. ч-ц; 3 — яд. фотоэмульсии, регистрирующие эти лавины; 4 — слои в-ва (Fe или Pb), тормозящего лавины заряж. ч-ц; 5 — импульсные ионизац. камеры.


Типичные габари­ты К. и.: высота 1,5—2 м, площадь поперечного сечения 1 м², масса 10—20 т.

• Григоров Н. Л., Рапопорт И. Д., Ш е с т о п е р о в В. Я., Частицы вы­соких энергий в космических лучах, М., 1973.

Н. Л. Григоров.

КАЛОРИМЕТРИЯ, совокупность ме­тодов измерения тепловых эффектов (кол-в теплоты), сопровождающих раз­личные физ., хим. и биол. процессы. К. включает измерения теплоёмкостей тел, теплот фазовых переходов (плав­ления, кипения и др.), тепловых эф­фектов намагничивания, электриза­ции, растворения, сорбции, хим. ре­акций (напр., горения), реакций об­мена в-в в живых организмах и т. д. Приборы, применяемые для калори­метрич. измерений, наз. калориметра­ми. Конструкция калориметров опре­деляется условиями измерений (в пер­вую очередь температурным интерва­лом измерений) и требуемой точностью. Калориметрич. измерения при темп-рах от 400 К (граница условна) и

240


выше наз. высокотемпера­турной К., а в области темп-р жидких азота, водорода и гелия (от ~77 К и ниже) — низкотемпе­ратурной К.

Результаты калориметрич. измере­ний находят широкое применение в теплотехнике, металлургии, хим. тех­нологии. Ими пользуются при рас­чётах кол-в теплоты, требуемых для нагрева, расплавления или испаре­ния в-в в разл. технол. процессах; для вычисления границ протекания хим. реакций и условий их проведе­ния. Так, область давлений и темп-р, в к-рой получают синтетич. алмазы из графита, была определена расчётом, в значительной мере основанным на ка­лориметрич. измерениях теплоёмко­сти и теплот сгорания этих в-в. Дан­ные низкотемпературной К. широко используются при изучении механич., магн. и электрич. эффектов в тв. те­лах и жидкостях, а также для расчёта термодинамич. ф-ций (напр., энтро­пии в-в).

В. Л. Соколов.

КАЛОРИЯ (от лат. calor — тепло) (кал, cal), внесистемная единица кол-ва теплоты. 1 кал=4,1868 Дж; К., применявшаяся в термохимии, рав­нялась 4,1840 Дж.

КАМЕРА-ОБСКУРА (от лат. camera obscura, букв.— тёмная комната), про­стейшее оптич. приспособление, поз­воляющее получать на экране изоб­ражения предметов. К.-о. представля­ет собой тёмный ящик с небольшим отверстием в одной из стенок, перед к-рым помещают рассматриваемый предмет. Лучи света, исходящие от разл. точек предмета, проходят через это отверстие и создают на противо­положной стенке ящика (экране) дей­ствительное перевёрнутое изображе­ние предмета. Оптимально резкое изо­бражение получается, когда радиус отверстия r составляет 0,95 радиуса первой зоны Френеля: r=0,95(d), где  — длина волны света, d — расстояние от отверстия до экрана.

С 17 в. К.-о. использовалась для наблюдения солн. затмений и для полу­чения перспективных рисунков, позд­нее была вытеснена линзовой каме­рой. К.-о. иногда применяется бла­годаря след, св-вам: 1) она даёт изо­бражение, свободное от дисторсии; 2) позволяет фотографировать объек­ты в таких лучах, для к-рых нельзя подобрать линзы, напр. К.-о. исполь­зуется при диагностике плазмы, при фотографировании разрядной трубки в рентг. лучах.

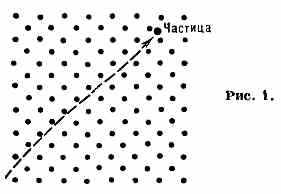
КАНАЛИРОВАНИЕ заряженных ча­стиц в кристаллах, движение ч-ц вдоль «каналов», образованных па­раллельными рядами атомов. Ч-цы испытывают скользящие столкнове­ния (импульс почти не меняется) с ря­дами атомов, удерживающих их в этих «каналах» (рис. 1). Если тра­ектория ч-цы заключена между дву­мя ат. плоскостями, то говорят о плоскостном К., в отличие от

аксиального К., при к-ром ч-ца движется между соседними ат. рядами или цепочками. К. было пред­сказано нем. физиком И. Штарком в 1912 и обнаружено лишь в 1963—65. К. тяжёлых ч-ц (протонов, поло­жит. ионов) наблюдается при их энергиях, больших неск. кэВ. При этом длина волны де Бройля ч-цы



мала по сравнению с постоянной крист. решётки, и К. может быть опи­сано законами классич. механики. Для К. необходимо, чтобы угол, обра­зуемый вектором скорости ч-цы с осью цепочки (или плоскостью канала), не превышал нек-рого критич. зна­чения _к, определяемого ф-лой:

_к=(Z₁Z₂/ξd) ,

где Z₁ и Z₂— заряды движущейся ч-цы и ядер атомов цепочки, ξ — энер­гия ч-цы, d — расстояние между со­седними атомами цепочки. Напр., при аксиальном К. протонов с энергией ξ=0,5 МэВ в монокристалле воль­фрама (Z₂=74e, e — заряд протона, d=3•10^-8 см) _к=2,3°, а мин. рас­стояние _к между траекторией ч-цы и осью цепочки равно: _к=0,3 Å (рис. 2). Все ч-цы, падающие на цепочку под углом <_к, будут зеркально отра­жаться от неё.



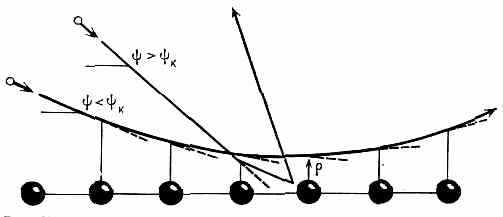
Рис. 2. Рассеяние ч-ц на цепочке атомов:  — угол падения ч-цы на цепочку; _к — критич. угол.


Электронная плотность в каналах меньше, чем в среднем в кристалле, и длина пробега ч-ц значительно боль­ше, чем вне его. Ч-цы могут выходить из канала в результате рассеяния на структурных дефектах решётки.

В случае К. эл-нов существенно влияние их волн. св-в и отрицат. за­ряда. При К. релятивистских заря­женных частиц возникает интенсив­ное электромагн. излучение (в гамма- и рентгеновских диапазонах). Для электронов и позитронов оно появля­ется при энергии ~1 МэВ.

• Тулинов А. Ф., Влияние кристалли­ческой решетки на некоторые атомные и ядер­ные процессы, «УФН», 1965, т. 87, в. 4, с. 585; Линдхард Й., Влияние кристалли­ческой решетки на движение быстрых заря­женных частиц, там же, 1969, т. 99, в. 2, с. 249; Томпсон М., Каналирование ча­стиц в кристаллах, пер. с англ., там же, с. 297; Меликов Ю. В., Тулинов А. Ф., Ядерные столкновения и кристаллы, «Природа», 1974, № 10, с. 39; Б а з ы л е в В. А., Ж е в а г о Н. К., Генерация интен­сивного электромагнитного излучения ре­лятивистскими частицами, «УФН», 1982, т. 137, в. 4.

Ю. В. Мартыненко.

КАНДЕЛА (от лат. candela— свеча) (кд, cd), единица СИ силы света; К.— сила света, испускаемого с пло­щади 1/600000 м² сечения полного излучателя (см. Световые эталоны) в перпендикулярном к этому сечению направлении при темп-ре излучателя, равной темп-ре затвердевания пла­тины (2042 К), и давлении 101 325 Па.

КАНДЕЛА НА КВАДРАТНЫЙ МЕТР (кд/м², cd/m²), единица СИ яркости; равна яркости светящейся плоской поверхности площадью 1 м² в пер­пендикулярном к ней направлении при силе света 1 кд. 1 кд/м²=10^-4 стильб = •10^-4 ламберт. Прежнее наименование ед.— нит.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕХАНИКИ (уравнения Гамильтона), дифференциальные ур-ния движения механич. системы (выведенные ирланд. учёным У. Гамильтоном в 1834), в к-рых переменными, кроме обобщён­ных координат q_i, явл. обобщённые импульсы р_i, совокупность q_i и р_i наз. канонич. переменными. К. у. м. имеют вид:



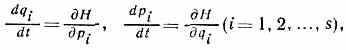
где H(q_i, р_i, t) — Гамильтона функ­ция, равная (когда связи не зависят от времени, а дей­ствующие силы по т е н ц и а л ь н ы) сумме кинетич. и потенц. энергий системы, выражен­ных через канонич. переменные; s — число степеней сво­боды системы. Ин­тегрируя эту сис­тему обыкновен­ных дифф. ур-ний 1-го порядка, мож­но найти все q_i и p_i как ф-ции времени t и 2s постоян­ных, определяемых по нач. данным. К. у. м. обладают тем важным св-вом, что позволяют с помощью т. н. канонич. преобразований перейти от q_i и р_i к новым канонич. переменным Q_i(q_i, p_i, t) и P_i(q_i, p_i, t). к-рые тоже удовлетворяют К. у. м., но с другой ф-цией Н(Q_i, Р_i, t). Так К. у. м. можно привести к виду, упрощающему процесс их интегрирования. Кроме классич. механики, К. у. м. исполь­зуются в статистич. физике, квант. механике, электродинамике и др. об­ластях физики.

С. М. Тарг.

241


КАНОНИЧЕСКИЙ АНСАМБЛЬ ГИББСА, статистический ансамбль для макроскопич. систем в тепловом рав­новесии с термостатом при пост. числе ч-ц в системе и пост. объёме. Такие системы можно рассматривать как малые части (подсистемы) статистич. ансамбля больших энергетически изо­лированных систем. При этом роль термостата играет вся система, кроме данной выделенной подсистемы. Вве­дён амер. физиком Дж. У. Гиббсом (J. W. Gibbs) в 1901 как одно из осн. понятий статистической физики. В К. а. Г. распределение по состояниям описывается каноническим распределе­нием Гиббса.

КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕ­НИЕ ГИББСА, распределение веро­ятностей состояний статистического ансамбля систем, к-рые находятся в тепловом равновесии со средой (тер­мостатом) и могут обмениваться с ней энергией при пост. объёме и пост. числе ч-ц (т. е. статистич. распределе­ние для канонического ансамбля Гиб­бса). Установлено Дж. У. Гиб­бсом (1901) как фундам. закон ста­тистической физики и обобщён в 1927 Дж. фон Нейманом (Германия) для квант. статистики.

Согласно К. р. Г., ф-ция распределе­ния, определяющая вероятность микроскопич. системы, равна:

f(p, q)=Z^-1e^{-H(p, q)/kT},

где Т — абс. темп-pa, Н(p, q) — Га­мильтона функция системы, (p, q) — обобщённые координаты (q) и им­пульсы (р) всех ч-ц системы, Z — ста­тистический интеграл, определяемый из условия нормировки функции f и равный:



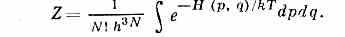
К. р. Г. можно вывести из микро­канонического распределения Гиббса, если рассматривать совокупность дан­ной системы и термостата как одну большую замкнутую изолированную систему и применить к ней микроканонич. распределение. Оказывается, что её малая подсистема обладает К. р. Г., к-рое можно найти интегри­рованием по всем фазовым перемен­ным термостата (теорема Гиббса).

В квантовой статистике статнстич. ансамбль характеризу­ется распределением вероятностей w_i квант, состояний системы с энергией ξ_i. Условие нормировки вероятности в квант. случае имеет вид _iw_i=1. Для всех Гиббса распределений в квант. случае w_i зависит лишь от уровней энергии ξ_i всей системы:

w_i=Z^-1e^-ξi/kT, где Z — статисти­ческая сумма, определяемая из условия нормировки и равная:



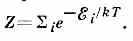
К. р. Г. в квант. случае можно также представить с помощью матрицы плот­ности =Z^-1e^-H/kT, где H — опе­ратор Гамильтона системы. К. р. Г. для квант. систем, как и для класси­ческих, можно вывести из микроканонич. распределения на основе теоре­мы Гиббса.

К. р. Г. как для классич., так и для квант. систем позволяет вычис­лить свободную энергию (Гельмгольца энергию) F=-kTlnZ, где Z — ста­тистич. сумма или интеграл. По най­денной свободной энергии можно опре­делить все др. потенциалы термодина­мические.

Д. Н. Зубарев.

КАОНЫ, то же, что К-мезоны.

КАПИЛЛЯРНАЯ КОНДЕНСАЦИЯ, конденсация пара в капиллярах и микротрещинах пористых тел, а также в промежутках между тесно сближен­ными тв. ч-цами или телами. Необхо­димое условие К. к.— смачивание жид­костью поверхности тела (ч-ц). К. к. начинается с адсорбции молекул пара поверхностью конденсации и образо­вания менисков жидкости. Т. к. имеет место смачивание, форма менисков в капиллярах вогнутая и давление насыщ. пара над ними р согласно Кельвина уравнению ниже, чем давле­ние насыщ. пара р₀ над плоской по­верхностью. Таким образом, К. к. происходит при более низких, чем p₀ давлениях. Объём жидкости, скон­денсировавшейся в порах, дости­гает предельной величины при р=р₀. В этом случае поверхность раздела жидкость — газ имеет нулевую кри­визну (плоскость, катеноид).

Сложная капиллярная структура пористого тела может служить при­чиной капиллярного ги­стерезиса — зависимости кол-ва сконденсировавшейся в капиллярах жидкости не только от р, но и от пре­дыстории процесса, т. е. от того, как было достигнуто данное состояние: в процессе конденсации или же в ходе испарения жидкости.

К. к. увеличивает поглощение (сорбцию) паров пористыми телами, в особенности вблизи точки насыще­ния паров. Процесс используется для улавливания жидкостей тонкопорис­тыми телами (сорбентами) и играет большую роль в процессах сушки, удержания влаги почвами, строитель­ными и др. пористыми материалами (см. Капиллярные явления).

Н. В. Чураев.

КАПИЛЛЯРНОЕ ДАВЛЕНИЕ, раз­ность давлений по обе стороны искрив­лённой поверхности раздела фаз (жид­кость — пар или двух жидкостей), вызванная поверхностным (межфаз­ным) натяжением. См. Капиллярные явления.

КАПИЛЛЯРНЫЕ ВОЛНЫ, малой длины волны на поверхности жидкости. В восстановлении равновесного состоя­ния поверхности жидкости при К. в. осн. роль играют силы поверхност­ного натяжения.

КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ, физ. явления, обусловленные поверхност­ным натяжением на границе разде­ла несмешивающихся сред. К К. я. относят обычно явления в жид­ких средах, вызванные искривлением их поверхности, граничащей с др. жидкостью, газом или собственным паром.

Искривление поверхности ведёт к появлению в жидкости дополнит. капиллярного давления Ар, величина к-рого связана со ср. кри­визной r поверхности ур-нием Лапла­са: p=p₁-р₂=2₁₂/r, где ₁₂— по­верхностное натяжение на границе двух сред; p₁ и р₂ — давления в жид­кости 1 и контактирующей с ней среде (фазе) 2. В случае вогнутой поверхно­сти жидкости (r<0) p_1
2 и р<0. Для выпуклых поверхностей (r>0) р>0. Капиллярное давление созда­ётся силами поверхностного натяже­ния, действующими по касательной к поверхности раздела. Искривление по­верхности раздела ведёт к появлению составляющей, направленной внутрь объёма одной из контактирующих фаз. Для плоской поверхности раздела (r=) такая составляющая отсут­ствует и р=0.

К. я. охватывают разл. случаи рав­новесия и движения поверхности жид­кости под действием сил межмолеку­лярного взаимодействия и внеш. сил (в первую очередь, силы тяжести). В простейшем случае, когда внеш. силы отсутствуют или скомпенсирова­ны, поверхность жидкости всегда ис­кривлена. Так. в условиях невесо­мости ограниченный объём жидкости, не соприкасающейся с др. телами, при­нимает под действием поверхност­ного натяжения форму шара (см. ст. Капля). Эта форма отвечает устой­чивому равновесию жидкости, по­скольку шар обладает мин. поверх­ностью при данном объёме и, следова­тельно, поверхностная энергия жид­кости в этом случае минимальна. Фор­му шара жидкость принимает и в том случае, если она находится в другой, равной по плотности жидкости (дей­ствие силы тяжести компенсирует­ся архимедовой выталкивающей си­лой).

Св-ва систем, состоящих из мн. мелких капель или пузырьков (эмуль­сии, жидкие аэрозоли, пены), и усло­вия их образования во многом опреде­ляются кривизной поверхности ч-ц, то есть К. я. Не меньшую роль К. я. играют и при образовании новой фа­зы: капелек жидкости при конденса­ции паров, пузырьков пара при кипе­нии жидкостей, зародышей тв. фазы при кристаллизации.

При контакте жидкости с тв. тела­ми на форму её поверхности сущест­венно влияют явления смачивания, обусловленные вз-ствием молекул жид­кости и тв. тела. На рис. 1 показан профиль поверхности жидкости, сма­чивающей стенки сосуда. Смачивание означает, что жидкость сильнее

242


вз-ствуст с поверхностью тв. тела (капилляра, сосуда), чем находящийся над ней газ. Силы притяжения, дейст­вующие между молекулами тв. тела и жидкости, заставляют её подни­маться по стенке сосуда, что приводит к искривлению при­мыкающего к стен­ке участка поверх­ности. Это создаёт отрицат. (капил­лярное) давление, к-рое в каждой точ­ке искривлённой



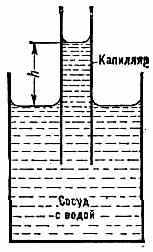
Рис. 1. Капиллярное поднятие жидкости, смачивающей стенки (вода в стеклянном со­суде и капилляре).


поверхности в точности уравновеши­вает дополнит. давление, вызванное подъёмом уровня жидкости. Гидро­статическое давление в объёме жид­кости при этом изменений не претер­певает.

Если сближать плоские стенки со­суда т. о., чтобы зоны искривления начали перекрываться, то образуется вогнутый мениск — полностью искрив­лённая поверхность. В жидкости под мениском капиллярное давление отри­цательно, под его действием жидкость всасывается в щель до тех пор, пока вес столба жидкости (высотой Л) не уравновесит действующее капилляр­ное давление р. В состоянии равно­весия (₁-₂)gh=р=2₁₂/r, где ₁ и ₂— плотность жидкости 1 и газа 2; g— ускорение свободного падения. Это выражение, известное как ф-ла Жюрена, определяет высоту h капил­лярного поднятия жидкости, полно­стью смачивающей стенки капилляра. Жидкость, не смачивающая поверх­ность, образует выпуклый мениск, что вызывает её опускание в капилляре ниже уровня свободной поверхности (h<0).

Капиллярное впитывание играет су­ществ. роль в водоснабжении расте­ний, передвижении влаги в почвах и др. пористых телах. Капиллярная про­питка разл. материалов широко при­меняется в процессах хим. техноло­гии.

Искривление свободной поверхно­сти жидкости под действием внеш. сил обусловливает существование т. н. капиллярных волн («ряби» на поверх­ности жидкости). К. я. при движении жидких поверхностей раздела рассмат­ривает физ.-хим. гидродинамика.

Движение жидкости в капиллярах может быть вызвано разностью ка­пиллярных давлений, возникающей в результате разл. кривизны поверх­ности жидкости. Поток жидкости на­правлен в сторону меньшего давления: для смачивающих жидкостей — к ме­ниску с меньшим радиусом кривизны (рис. 2, а).

Пониженное, в соответствии с Кель­вина уравнением, давление пара над

смачивающими менисками явл. при­чиной капиллярной конденсации жид­костей в тонких порах.

Отрицательное капиллярное давле­ние оказывает стягивающее действие на ограничивающие жидкость стенки(рис. 2, б).



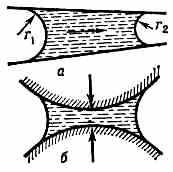
Рис. 2. а — переме­щение жидкости в ка­пилляре под дейст­вием разности капил­лярных давлений (r₁>r₂); б — стягива­ющее действие капил­лярного давления (напр., в капилляре с эластичными стен­ками).


Это может приводить к значит. объёмной деформации высоко­дисперсных систем и пористых тел — капиллярной контракции. Так, напр., происходящий рост капиллярного давления при высу­шивании приводит к значит. усадке материалов.

Многие св-ва дисперсных систем (проницаемость, прочность, поглоще­ние жидкости) в значит. мере обуслов­лены К. я., т. к. в тонких порах этих тел реализуются высокие капиллярные давления.

К. я. впервые были открыты и ис­следованы Леонардо да Винчи (1561), Б. Паскалем (17 в.) и Дж. Жюреном (Джурин, 18 в.) в опытах с капилляр­ными трубками. Теория К. я. развита в работах П. Лапласа (1806), Т. Юнга (Янг, 1805), Дж. У. Гиббса (1875) и И. С. Громеки (1879, 1886).

• А д а м Н. К., Физика и химия поверхнос­тей, пер. с англ., М., 1947; Громека И. С., Собр. соч., М., 1952.

Н. В. Чураев.