От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Каустическая поверхность Качественный спектраль­ный анализ Квадрупольное взаимодей­ствие Квадрупольный мо­мент ядра). Квадрупольное излучение Квадрупольные линзы Квадрупольный масс-спект­рометр Квадрупольный момент ядра В. П. Парфёнова. Квазиволновой вектор Квазиклассическое прибли­жение Квазинейтральность плазмы Квазиодномерные проводни­ки Кписталлическая структу­ра K В. С. Эдельман, Э. М. Эпштейн. В. И. Таланов, М. А. Миллер. Квазистационарное состоя­ние Квазиупругая сила

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КАТОПТРИКА (от греч. katoptrikos — зеркальный, отражённый в зер­кале), историческое, ныне устар. наз­вание раздела геометрической оптики, в к-ром рассматривались оптич. св-ва отражающих поверхностей (зеркал оп­тических) и систем зеркал.

КАУСТИЧЕСКАЯ ПОВЕРХНОСТЬ (от греч. kaustikos — палящий) в оп­тике, поверхность, огибающая семей­ство световых лучей, испущенных све­тящейся точкой и прошедших через оптич. систему. Иначе, К. п.— поверх­ность, в каждой точке к-рой пересе­каются после преломлений на грани­цах оптич. сред системы два луча, расходящиеся от светящейся точки под очень малым углом. К. п. хорошо видна в задымлённой среде, т. к. на ней концентрируется световая энер­гия. По св-вам симметрии К. п. мож­но классифицировать аберрации опти­ческих систем. Напр., осесимметричная К. п. соответствует сферической абер­рации, К. п., симметричная относи­тельно к.-л. меридиональной плоскос­ти,— коме. У безаберрац. оптич. си­стем К. п. обращается в точку — изображение точечного источника.

КАЧЕСТВЕННЫЙ СПЕКТРАЛЬ­НЫЙ АНАЛИЗ, анализ хим. состава в-ва (без определения концентраций) по его спектру путём его сопоставле­ния с известными спектрами в-в. Атомный К. с. а. осуществляется с помощью таблиц и атласов, молеку­лярный — преим. на ЭВМ, в память к-рых введены спектр. данные мн. в-в. К К. с. а. относится и анализ струк­туры молекул по спектрам. См. Спект­ральный анализ.

КВАДРУПОЛЬ (от лат. quadrum -четырёхугольник, квадрат и греч. polos — полюс), электрически нейт­ральная система заряж. ч-ц, к-рую можно рассматривать как совокуп­ность двух диполей с равными по величине, но противоположными по знаку дипольными моментами, распо­ложенных на нек-ром расстоянии а друг от друга (рис.). Осн. хар-ка К.— его квадрупольный момент Q (для К., изображённых на рисунке, Q=2ela, где е — абс. величина электрич. заряда, l — размер диполей).

246


На больших расстояниях R от К. напряжённость электрического поля Е убывает обратно пропорц. R⁴, а зависимость Е от зарядов и их рас­положения описывается в общем случае набором из пяти независимых величин, к-рые вместе составляют квадрупольный момент системы. Квадрупольный момент определяет также энергию К. во внешнем, медленно меняющемся электрич. поле. К. явл. мультиполем 2-го порядка.




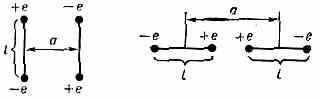
Примеры относит. расположения диполей в квадруполе.

КВАДРУПОЛЬНОЕ ВЗАИМОДЕЙ­СТВИЕ, взаимодействие систем заряж. ч-ц, обусловленное наличием у этих систем квадрупольного момента (см. Квадруполь). Если электрич. заряд или .дипольный момент систем отлич­ны от нуля, то К. в. можно пренебречь, т. к. оно по порядку величины зна­чительно меньше электростатич. и дипольного вз-ствий.

К. в. существенно для вз-ствия ато­мов на больших расстояниях, если квадрупольный момент обоих атомов отличен от нуля. Энергия К. в. ато­мов (не обладающих электрич. дипольным моментом) убывает с увеличе­нием расстояния R пропорц. 1/R⁵, в то время как энергия вз-ствия дипольных моментов, наводимых в этих атомах вследствие их взаимной поля­ризуемости, меняется с расстоянием пропорц. 1/R⁸. Поэтому К. в. атомов на больших расстояниях оказывается доминирующим. Квадрупольные мо­менты атомов могут быть рассчитаны методами квант. механики.

Квадрупольным моментом обладают мн. ат. ядра, распределение электрич. заряда в к-рых не обладает сферич. симметрией (см. Квадрупольный мо­мент ядра). К. в. играет большую роль в яд. физике при возбуждении ядер с нулевым дипольным моментом кулоновским полем налетающих на ядра заряж. ч-ц.

Г. Я. Мякишев

КВАДРУПОЛЬНОЕ ИЗЛУЧЕНИЕ,

излучение эл.-магн. волн, обуслов­ленное изменением во времени элект­рич. квадрупольного момента (см. Квадруполь) излучающей системы. Излучение, возникающее при измене­нии магн. квадрупольного момента, наз. магн. К. и. или просто магн. излучением. См. Мультипольное из­лучение, Излучение.

КВАДРУПОЛЬНЫЕ ЛИНЗЫ, см. Электронные линзы.

КВАДРУПОЛЬНЫЙ КОНДЕНСА­ТОР, система четырёх электродов в виде стержней (круглого или близ­кого к квадратному поперечного се­чения), расположенных симметрично относительно центр. оси и параллель­но ей. Противоположные (относительно оси) стержни соединены попарно, между парами приложена разность потенциалов. К. к. используется как анализатор масс (см. рис. 7 в ст. Масс-спектрометр), для сортировки атомов и молекул по энергетич. со­стояниям (см. Молекулярный генера­тор) и т. д.

КВАДРУПОЛЬНЫЙ МАСС-СПЕКТ­РОМЕТР, устройство, в к-ром разде­ление ионов по величине отношения массы к его заряду осуществляется в электрич. поле квадрупольного кон­денсатора. См. Масс-спектрометр.

КВАДРУПОЛЬНЫЙ МОМЕНТ ЯДРА, величина, характеризующая определённого рода отклонение распре­деления электрич. заряда в ат. ядре произведением eQ, где е — элементар­ный электрич. заряд, Q—коэфф., имею­щий размерность площади (обычно выражается в см²) и равный ср. зна­чению 2(3cos²-1)>, где r — расстояние элемента заряда от начала координат,  — полярный угол соот­ветствующего радиуса — вектора (по­лярная ось направлена по спину ядра). Для сферически симметричного ядра Q=0. Если ядро вытянуто вдоль оси симметрии, то Q>0, если сплюсну­то, то Q<0. К. м. я. изменяется в широких пределах, напр. для ядра ¹⁷₈O Q= -0.027•10^-24 см², для ядра ²⁴¹₉₃Am Q=4,9•10^-24 см². Как прави­ло, большие К. м. я. положительны. Это означает, что при значит. откло­нении от сферич. симметрии заряд ядро имеет форму вытянутого эллип­соида вращения. См. Ядро атомное.

В. П. Парфёнова.

КВАЗАРЫ (англ. quasar, сокр. от quasi-stellar radiosource — квази­звёздный источник радиоизлучения), мощные внегалактич. источники эл.-магн. излучения; представляют собой активные ядра далёких галактик. Открыты в 1960 как звездообразные источники радиоизлучения с очень малыми угл. размерами (меньше 10") и малой визуальной звёздной величи­ной (типичные значения m_V~ 16— 18^m). В 1963 в спектрах К. было обнаружено значит. красное смещение (г) спектр. линий, указывающее на большую удалённость К. (все К. на­ходятся дальше 200 Мпс, а у одного из К. z=3,53, т. е. он близок к гра­нице видимой Вселенной). С учётом расстояния до К. мощность излучения типичного К. составляет в радиодиа­пазоне ~ 10⁴³ эрг/с, в оптич. диапа­зоне ~ 10⁴⁶ эрг/с, в ИК диапазоне .~10⁴⁷ эрг/с, т. е. излучение К. в 10³—10⁴ раз превышает излучение всех звёзд крупной галактики (у К. 3С273 обнаружено также рентг. излу­чение ~ 10⁴⁶ эрг/с). По избыточному УФ излучению К. удаётся отличить от норм. звёзд, а по сильному ИК излу­чению — от белых карликов. К фундам. св-вам К. относится переменность их излучения в радио-, ИК- и оптиче­ском диапазонах (наименьшая времен­ная вариация т ~ 1 ч). Поскольку раз-

меры переменного по блеску объекта не могут превышать c., размеры К. 4•10¹² м (т. е. меньше диаметра орбиты Урана).

Физ. природа активности К. ещё до конца не раскрыта. Существует предположение, что активная фаза ядер галактик составляет сравни­тельно небольшую часть времени их существования и что эта фаза может периодически повторяться. Согласно существующим гипотезам, мощное из­лучение К. (как тепловое, так и синхронное) может быть обусловле­но: 1) процессами в компактном (~10⁸ m_солн — солн. масс) звёздном скоплении (столкновения звёзд, вспышки сверхновых, ансамбль пуль­саров); 2) трансформацией в излуче­ние энергии магн. полей и кинетич. энергии массивного вращающегося магнитоплазмеиного тела; 3) аккре­цией в-ва на массивную чёрную дыру, находящуюся в центре К. Раскрытие энергетики К. внесёт, несомненно, существенный вклад в совр. физику и астрофизику. Особый интерес К. представляют как далёкие объекты, участвующие в космологич. расшире­нии Метагалактики. Исследование пространств. распределения К. и различий в их св-вах может пролить свет на ранние стадии эволюции Все­ленной (см. Космология).

• Б е р б и д ж Дж., Б е р б и д ж М., Квазары, пер. с англ., М., 1969; Происхож­дение и эволюция галактик и звезд, под ред. С. Б. Пикельнера, М., 1976; X е й Дж., Радиовселенная, пер. с англ., М., 1978.

КВАЗИВОЛНОВОЙ ВЕКТОР, вектор­ная величина k, характеризующая состояние ч-цы (или квазичастицы) в периодич. поле крист. решётки. К. в. похож на волновой вектор; отлича­ется от квазиимпульса р численным множителем: k=p/h.

КВАЗИИМПУЛЬС, векторная вели­чина р, характеризующая состояние ч-цы или квазичастицы (напр., эл-на) в периодич. поле крист. решётки. По своим св-вам К. похож на импульс так же, как квазиволновой вектор на волновой вектор. При столкнове­ниях ч-ц закон сохранения К. слож­нее, чем закон сохранения импульса: К. либо сохраняется, либо изменяется на дискр. величину. КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИ­ЖЕНИЕ квантовой механики (Венцеля — Крамерса — Бриллюэна ме­тод), приближённый метод решения задач квант. механики, применимый, когда и квант. и классич. описание движения ч-цы дают близкие резуль­таты; впервые использован нем. физи­ком Г. Венцелем, англ. физиком Г. Крамерсом и франц. физиком Л. Бриллюэном в 1926. С точки зрения общей теории волн. полей К. п. соот­ветствует такому описанию, при к-ром основным явл. рассмотрение лучей («геом. приближение»), а «волновые» эффекты выступают как малые по-

247


правки. Такое описание приемлемо, если длина волны (в квант. механике — длина волны де Бройля) достаточно мала — много меньше всех масшта­бов неоднородностей действующих на ч-цу внеш. полей. Кроме того, необ­ходимо, чтобы длина волны медленно менялась от точки к точке. Т. к. длина волны де Бройля  равна отношению постоянной Планка h к импульсу р, к-рый связан с полной ξ и потенци­альной U(х) энергиями соотношением ξ=р²/2m+U(х) (где х — координата), К. п. применимо лишь в случаях, когда U(х) меняется достаточно мед­ленно с изменением х.

Формально К. п. сводится к вычис­лению действия S в виде разложения в ряд: S=S₀+S₁+S₂+.., первый член к-рого не зависит от h (классич. действие S₀), второй пропорц. h, третий пропорц. h² и т. д. Найдя S, можно получить и волн. ф-цию , равную: =ехр(2iS/h). Обычно ограничива­ются членом S₁. Получаемая при этом

 наз. квазиклассич. волн. ф-цией, _кп.

Важный частный случай — движе­ние ч-цы в конечной области пр-ва. При таком финитном движении внутри нек-рой потенциальной ямы К. п. не может быть применимым везде; это ясно хотя бы из того, что, доходя до «стенки» ямы, ч-ца (на языке клас­сич. физики) на мгновение останавли­вается, т. е. р обращается в нуль, а следовательно, . Для окрест­ностей вблизи таких точек поворота нужно искать  на основе точного квантовомеханич. Шредингера урав­нения, а затем потребовать, чтобы между _кп и  был непрерывный пе­реход при приближении к точкам поворота. Оказывается, что из тре­бований этой непрерывности и одно­значности  без дополнит. предполо­жений вытекают условия квантова­ния Бора.

Применимость К. п. оправдана лишь при больших значениях квантовых чисел.

• См. лит. при ст. Квантовая механика.

В. II. Григорьев.

КВАЗИНЕЙТРАЛЬНОСТЬ ПЛАЗМЫ, одно из важнейших св-в плазмы, за­ключающееся в практически точном ра­венстве плотностей входящих в её состав положит. ионов и эл-нов. В этом случае пространств. заряды эл-нов и ионов компенсируют друг друга, так что полное поле внутри равновес­ной плазмы равно нулю. К. п. имеет место, если линейные размеры обла­сти, занимаемой плазмой, много боль­ше дебаевского радиуса экранирования D. Вблизи границы плазмы, где более быстрые эл-ны вылетают за счёт теп­лового движения на длину D, К. п. может нарушаться.

КВАЗИОДНОМЕРНЫЕ ПРОВОДНИ­КИ, кристаллич. вещества, у к-рых электропроводность вдоль избранного

направления ст.. значительно превы­шает электропроводность  в пер­пендикулярной плоскости : _║>>.

Такая анизотропия св-в связана с осо­бенностями крист. строения, из-за к-рых движение эл-нов в кристалле явл. одномерным. Так, в решётке, образованной комплексами, содержа­щими атомы переходных металлов,

напр. в кристалле R₂Pt (CN₄)B_0,3•ЗН₂O (рис.), атомы Pt об­разуют параллельные цепочки, окружённые группами CN. Благо­даря малому расстоя­нию (2,88 А) между атомами Pt в цепочке электронные оболочки атомов Pt сильно пере­крываются, в резуль­тате чего становится возможным переход эл-нов от одного ато­ма Pt к другому, т. е. возможен электрич. ток вдоль цепочки. Электропроводность кристалла вдоль оси с оказывается доволь­но высокой [при ком­натной температуре _║=3•10² (Ом•м)^-1, _║/ 2•10²].

Другой класс К. п. образуют в-ва, молекулы к-рых содержат комплекс тетрацианохинодиметана (TCNQ). При кристаллизации эти комплексы выстраиваются в линейные цепочки, что обусловливает проводимость вдоль цепочек [_║ = 2•10² (Ом•м)^-1, _║/~10—10³].

Известны К. п. с ПП и металлич. типами проводимости. Чисто метал­лич. проводимость у макроскопич. образцов наблюдать не удаётся, т. к. неизбежные структурные дефекты приводят к разрывам проводящих цепочек, имеющих поперечные раз­меры порядка атомных. Чтобы прео­долеть места разрывов, эл-н должен обладать заметной энергией. Прово­димость всех известных К. п. носит активац. хар-р, т. е. при T300—400 К ~ехр(-/T), где  — энер­гия активации (~10^-1—10^-2 эВ). При малой  наблюдаются диэлектрич. св-ва К. п, (диэлектрич. проницае­мость =10³).

Исследование К. п. в значит. сте­пени было стимулировано идеей У. А. Литла (США, 1964) о возмож­ности высокотемпературной сверхпро­водимости в одномерных проводниках. Однако оказалось, что все известные

К. п. с металлич. проводимостью неустойчивы по отношению к измене­нию периода крист. решётки (в про­стейшем случае к удвоению), к-рое сопровождается расщеплением частич­но заполненной зоны проводимости на целиком заполненную подзону и пу­стые подзоны. В результате при по­нижении темп-ры К. п. претерпевает переход в диэлектрич. состояние



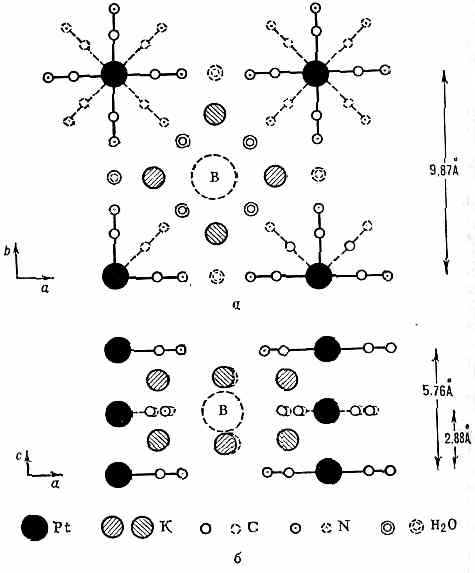
Кписталлическая структу­ра K₂Pt(CN₄)B_0,3•2,7H₂O: а — в плоскости аb; б — в плоскости ас.


(переход Пайерлса). Этот переход сопровождается перестройкой фононного спектра (что проявляется в экспериментах по рассеянию нейтро­нов или рентг. лучей), изменением оптич. св-в, проводимости, электрон­ной теплоёмкости, парамагн. воспри­имчивости и т.д. Переход К. п. в диэлектрич. состояние может быть также связан с межэлектронным вз-ствием (переход Мотта).

К. п. могут быть созданы помеще­нием металла в сильное магн. поле H. Благодаря поперечному магнетосопротивлению p~H²; в совершенных монокристаллах металлов при Т~ ~4 К уже в полях Н порядка неск. кЭ достигается _║/~ 10³—10⁶.

Двухмерная слоистая крист. струк­тура может привести к квазидвумер­ной проводимости; пример — графит, обладающий гексагональной струк­турой с межплоскостным расстоянием вдоль оси 6,69Å и межат. расстоянием в гексагональной плоскости 2,45Å. Это различие приводит к /_║ 10⁴.

• Овчинников А. А., Украин­ский И. И., Квенцель Г. Ф., Теория одномерных моттовских полупроводников и электронная структура длинных молекул с сопряженными связями, «УФН», 1972, т. 108-в. 1, с. 81; Б у л а е в с к и й Л. Н., Струк-

248


турный (пайерлсовский) переход в квазиод­номерных кристаллах, там же, 1975, т. 115. в. 2, с. 263; Проблема высокотемпературной сверхпроводимости, М., 1977.

В. С. Эдельман, Э. М. Эпштейн.

КВАЗИОПТИКА, оптика широких волн. пучков, занимающая промежу­точное положение между СВЧ элект­родинамикой, где строго учитываются дифракц. эффекты, и геометрической оптикой, где ими полностью пренеб­регают. В К. дифракц. явления учи­тываются лишь в той мере, в какой они существенны при описании распро­странения достаточно протяжённых широких волн. пучков. Представле­ниями же геом. оптики пользуются при описании трансформации этих пучков линзами, зеркалами, призмами и т. п.

Обособившись в самостоят. раздел электродинамики в период освоения диапазона миллиметровых волн, К. в дальнейшем приобрела универсаль­ный хар-р как аппарат, пригодный для волн любой природы и в любом диа­пазоне длин волн, если только вы­полнен необходимый критерий её применимости — достаточное превы­шение поперечных размеров волн. пуч­ка над длиной волны .

Квазиоптич. электродинамич. си­стемы заменили традиционные в СВЧ диапазоне одномодовые объёмные ре­зонаторы и радиоволноводы при пере­ходе в диапазоны миллиметровых, субмиллиметровых и оптич. длин волн. Прежние системы оказались непри­годными из-за уменьшения размеров, повышения требований на точность изготовления элементов, снижения электрич. прочности, а главное — значит. возрастания потерь в экра­нирующих проводниках. Использо­вать же экранированные системы с раз­мерами d >> (т. н. сверхразмерные волноводы и резонаторы) оказалось затруднительным вследствие уплот­нения спектра собственных частот, практически сливающегося в сплош­ной спектр из-за уширения линий. В квазиоптических резонаторах можно сгруппировать часть мод в пучки, практически оторванные от боковых стенок резонатора и сохра­няющие свою структуру при устра­нении этих стенок вообще. Так был совершён переход от полностью экра­нированных систем к открытым, представляющим собой системы зер­кал спец. (обычно сферического) про­филя, корректирующих дифракц. уширение пучка (см. Оптический ре­зонатор). На аналогичных принципах строятся и квазиоптич. открытые ли­нии передачи, в к-рых волновой пучок формируется последовательностью длиннофокусных линз или эллиптич. зеркал (корректоров). Как в открытых волноводах, так и в открытых резона­торах потери на излучение, различ­ные для разных мод, играют опреде­ляющую роль в разрежении спектра (селекция мод). В ряде техн. прило­жений (напр., волоконная оптика), а также в задачах распространения волн

(ионосферные волноводы, подводный звуковой канал и др.) используются квазиоптич. линии, практически одно­родные вдоль трассы. Формирование пучков осуществляется поперечной неоднородностью сред.

Основу матем. аппарата К. состав­ляют метод интегральных преобразо­ваний и метод параболич. ур-ния, ча­ще применяемых в непрерывных си­стемах. Наряду с линейной К. по­лучила развитие и К. нелинейных сред.

• Техника субмиллиметровых волн, под ред. Р. А. Валитова, М., 1969; Квазиоптика, пер. с англ. и нем., под ред. Б. 3. Каценеленбаума и В. В. Шевченко, М., 1966.

В. И. Таланов, М. А. Миллер.

КВАЗИСТАТИЧЕСКИЙ ПРОЦЕСС (равновесный процесс), в термодина­мике — бесконечно медленный пере­ход термодинамич. системы из одного равновесного состояния в другое, при к-ром в любой момент времени физ. состояние системы бесконечно мало отличается от равновесного (см. Рав­новесие термодинамическое). Равно­весие в системе при К. п. устанавли­вается во много раз быстрее, чем про­исходит изменение физ. параметров системы. Всякий К. п. явл. обрати­мым процессом. К. п. играют в термо­динамике важную роль, т. к. термо­динамич. циклы, включающие одни К. п., дают макс. значения работы (см. Карно цикл). Термин «К. п.» предло­жен в 1909 нем. математиком К. Каратеодори.

КВАЗИСТАЦИОНАРНОЕ СОСТОЯ­НИЕ, то же, что метастабильное состояние.

КВАЗИСТАЦИОНАРНЫЙ ТОК, от­носительно медленно изменяющийся перем. ток, для мгновенных значений к-рого с достаточной точностью выпол­няются законы пост. токов (Ома закон, Кирхгофа правила и т. д.). Подобно пост. току, К. т. имеет одинаковую силу тока во всех сечениях неразветв­лённой цепи. Однако при расчётах К. т. (в отличие от расчёта цепей пост. тока) необходимо учитывать возни­кающую при изменениях тока эдс электромагнитной индукции. Ин­дуктивности, ёмкости, сопротивления ветвей цепи К. т. могут считаться сосредоточенными параметрами.

Для того чтобы данный перем. ток можно было считать К. т., необходимо выполнение условия квазистационар­ности, к-рое для синусоидальных пе­рем. токов сводится к малости геом. размеров электрич. цепи по сравнению с длиной волны рассматриваемого то­ка. Токи пром. частоты, как правило, можно считать К. т. (частоте 50 Гц соответствует дл. волны ~ 6000 км). Исключение составляют токи в линиях дальних передач.

КВАЗИУПРУГАЯ СИЛА, направлен­ная к центру О сила F, величина к-рой пропорц. расстоянию r от цент­ра О до точки приложения силы; численно F=cr, где с — пост. коэф­фициент. Тело, находящееся под дей­ствием К. с., обладает потенц. энергией П=cr²/2. Назв. «К. с.» связано с тем, что аналогичным св-вом обладают силы, возникающие при малых де­формациях упругих тел (т. н. силы упругости). Для материальной точки, находящейся под действием К. с., центр О явл. положением устойчивого равновесия. Выведенная из этого положения точка будет совершать около О линейные гармонические ко­лебания или описывать эллипс (в частности, окружность).