От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Момент количества движения. Системы многих частиц. Тождествен­ные частицы. Паули принципом. Обменное взаимодействие. Химиче­ская связь. L в данном состоянии определяется коэфф. с L можно найти непосред­ственно через L В. Б. Берестецкий.

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

Временное уравнение Шредингера. До сих пор рассматривались лишь воз­можные квант. состояния системы и не рассматривалась эволюция си­стемы во времени (её динамика). Полное решение задач К. м. должно давать  как ф-цию координат и вре­мени t. Для одномерного движения (вдоль оси х) она определяется ур-нием



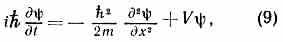
являющимся ур-нием движения в К. м. и наз. временным урав­нением Шредингера. Оно спра­ведливо и в случае, когда потенц. энергия зависит от времени: V=V(х, t). Частными решениями ур-ния (9) явл. ф-ции



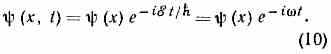
Здесь ξ — энергия ч-цы, a (х) удов­летворяет стационарному ур-нию Шре­дингера (7); для свободного движения (х) представляет собой волну де Бройля e^ikx и (x, t) = e^i(kx-t). Волн. ф-ции (10) обладают тем важ­ным св-вом, что соответствующие рас­пределения вероятностей не зависят от времени, т. к. │(x,t)│²=│(x)│². Поэтому состояния, описываемые та­кими волн. ф-циями, наз. стацио­нарными; они играют особую

роль в приложениях К. м. Общим ре­шением временного ур-ния Шредин­гера явл. суперпозиция стационарных состояний. В этом (нестационарном) случае, когда вероятности сущест­венно меняются со временем, энергия ξ системы не имеет определ. значе­ния. Так, если (x, t)=С₁e^{(k1x-1t)}+ + C₂e^i(k2x-2t}, то ξ =Ћ₁ с вероят­ностью |С₁|² и ξ=Ћ₂ с вероятно­стью |С₂|². Для энергии и времени существует соотношение неопределён­ностей:

ξt~ћ, (11)

где ξ — дисперсия энергии, а t — промежуток времени, в течение к-рого энергия может быть измерена.

Трёхмерное движение. В общем слу­чае движения ч-цы в трёх измерениях волн. ф-ция зависит от координат х, у, z и времени: =(х, у, z, t), а волна де Бройля имеет вид:



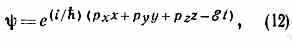
где р_х, p_y, p_z — три проекции им­пульса на оси координат, а ξ= (p²_x+p²_y +p²_z)/2m. Соотв. имеются три соотношения неопределённостей:



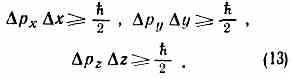
Временное ур-ние Шредингера имеет вид:



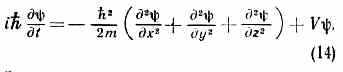
Это ур-ние принято записывать в символич. форме:



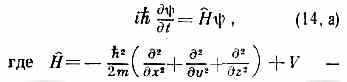
дифф. оператор, наз. оператором Га­мильтона или гамильтонианом. Ста­ционарным решением ур-ния (14) яв­ляется



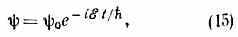
₀ — решения ур-ния Шрединге­ра для стационарных состояний:



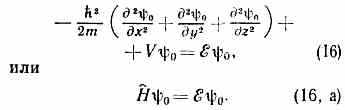
При трёхмерном движении спектр энергии также может быть непрерыв­ным и дискретным. Возможен и слу­чай, когда неск. разных состояний, описываемых разными волн. ф-ция­ми, имеют одинаковую энергию; такие состояния наз. вырожденными. В случае непрерывного спектра ч-ца уходит на бесконечно большое рас­стояние от центра сил. Но, в отличие от одномерного движения (когда бы­ли только две возможности — про-

258


хождение или отражение), при трёх­мерном движении ч-ца может удалить­ся от центра под произвольным углом к направлению первонач. движения, т. е. рассеяться. Волн. ф-ция ч-цы теперь явл. суперпозицией не двух, а бесконечного числа волн де Бройля, распространяющихся по всевозможным направлениям. Рас­сеянные ч-цы удобно описывать в сферич. координатах, т. е. определять их положение расстоянием от центра (ра­диусом) r и двумя углами — широтой  и азимутом . Соответствующая волн. ф-ция на больших расстояниях от центра сил имеет вид:



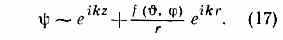
Первый член (пропорц. волне де Брой­ля, распространяющейся вдоль оси z) описывает падающие ч-цы, а второй (пропорц. «радиальной волне де Брой­ля») — рассеянные. Ф-ция f(, ) наз. амплитудой рассеяния; она определяет дифф. сечение рассеяния da, характеризующее ве­роятность рассеяния под данными углами:

d=|f(, )|²d, (18)

где d — элемент телесного угла, в к-рый происходит рассеяние.

Дискр. спектр энергии возникает (как и при одномерном движении), когда ч-ца оказывается внутри потенц. ямы. Уровни энергии нумеруют квант. числами, причём, в отличие от од­номерного движения, не одним, а тремя.

Момент количества движения. Очень важной задачей явл. движение в поле центр. сил притяжения. Угл. часть движения (вращение) определяется в К. м., как и в классической, заданием момента кол-ва движения М, к-рый при движении в поле центр. сил сохра­няется. Но, в отличие от классич. механики, в К. м. момент может при­нимать только вполне определённые дискр. значения, т. е. имеет дискр. спектр. Это можно показать на при­мере орбитального (азимутального) движения ч-цы — вращения вокруг заданной оси (принимаемой за ось z). Волн. ф-ция в этом случае имеет вид «угл. волны де Бройля» е^im, где  — азимут, а число m так же связано с моментом M_z, как в пло­ской волне де Бройля волн. число k с импульсом р, т. е. m=М_z/ћ. Т. к. углы  и +2 описывают одно и то же положение системы, то и волн. ф-ция при изменении  на 2 должна возвращаться к прежнему значению. Отсюда вытекает, что т может при­нимать только целые значения: m=0, ±1, ±2,..., т.е. М_z может быть ра­вен:

M_z=mћ=0, ±ћ, ±2ћ, ... (19)

Вращение вокруг оси z — только часть угл. движения (проекция дви­жения на плоскость ху), а М_z — про­екция полного момента М на ось r.

Для определения М надо знать две остальные его проекции. Но в К. м. три составляющие момента не могут одновременно иметь точные значения. Действительно, проекция момента содержит произведение проекции им­пульса на соответствующее плечо — координату, перпендикулярную им­пульсу, а все проекции импульса и все плечи, согласно соотношениям неопределённостей (13), одновременно не могут принимать точно определ. значения. Оказывается, что кроме M_z, задаваемой числом m, можно одновременно точно задать величину момента, определяемую целым числом l:

M²=ћ²l(l+1), l=0, 1, 2, ... (20)

Т. о., при описании угл. движения ч-цы вводятся два квант. числа — l и т. Число l наз. орбитальным квантовым числом; от него может зависеть значение энергии ч-цы (как в классич. механике от вытянутости орбиты). Число т наз. маг­нитным квантовым числом и при данном l может принимать значения 0, ±1, ±2, ..., ±l — всего 2l+1 значений; от m энергия не зави­сит, т. к. само значение т зависит от выбора оси z, а поле сферически симме­трично. Поэтому уровень с квант. числом l имеет (2l+1)-кратное вырож­дение. Энергия уровня начинает за­висеть от т лишь тогда, когда сферич. симметрия нарушается, напр. при помещении системы в магн. поле (Зеемана эффект).

При заданном моменте радиальное движение похоже на одномерное дви­жение с тем отличием, что вращение вызывает центробежные силы. Их учитывают введением (кроме обычной потенц. энергии) центробежной энер­гии М²/2m₀r²=ћ²l(l+1)/2m₀r² (здесь m₀ — масса ч-цы). Решение ур-ния Шредингера для радиальной части волн. ф-ции атома определяет его уровни энергии; при этом вводится третье квант. число — радиаль­ное n_r или главное n, к-рые связаны соотношением: n=n_r+l+1, n_r=0, 1, 2, ..., n=1, 2, 3, ... . В част­ности, для движения эл-на в кулоновском поле ядра с зарядом Ze (водородоподобный атом) уровни энергии определяются ф-лой:



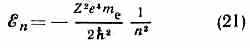
(m_e — масса эл-на), т. е. энергия за­висит только от га. Для многоэлект­ронных атомов, в к-рых каждый эл-н движется не только в поле ядра, но и в поле остальных эл-нов, уровни энер­гии зависят также и от l.

На рис. 3 в статье Атом приведены распределения электронной плотности вокруг ядра в атоме водорода для со­стояний с низшими значениями квант. чисел n, l и m. Видно, что задание момента (чисел l и m) полностью определяет угл. распределение. В ча­стности, при l=0(M²=0) распределение электронной плотности сфери­чески симметрично. Т. о., квант. дви­жение при малых l совершенно непо­хоже на классическое. Так, сферически симметричное состояние со ср. зна­чением радиуса r0 отвечает как бы классич. движению по круговой орбите (или по совокупности круговых орбит, наклонённых под разными углами), т. е. движению с ненулевым момен­том. Это различие между квантовоме­ханич. и классич. движениями — следствие соотношения неопределён­ностей и может быть истолковано на его основе. При больших квант. числах длина волны де Бройля ста­новится значительно меньше расстоя­ний L, характерных для движения данной системы:



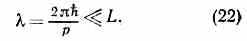
В этом случае квантовомеханич. за­коны движения приближённо пере­ходят в классич. законы движения ч-ц по определ. траекториям, подобно тому как законы волн. оптики в аналогичных условиях переходят в законы геом. оптики. Условие мало­сти де-бройлевской длины волны (22) означает, что pL >>ћ, где pL по поряд­ку величины равно классич. действию для системы. В этих условиях квант действия ћ можно считать очень малой величиной, т. е. формально переход квантовомеханич. законов в класси­ческие осуществляется при ћ0. В этом пределе исчезают все спецнфич. квантовомеханич. явления, напр. обращается в нуль вероятность тун­нельного эффекта.

Спин. В К. м. ч-ца (как сложная, напр. ядро, так и элементарная, напр. эл-н) может иметь собств. момент кол-ва движения, наз. спином. Это означает, что ч-це можно приписать квант. число (J), аналогичное орбит. квант. числу l. Квадрат собств. мо­мента кол-ва движения имеет величину ћ²/(J+1), а проекция момента на определ. направление может прини­мать 2J+1 значений от -ћJ до +ћJ с интервалом ћ. Т. о., состояние ч-цы (2J+1)-кратно вырождено. Поэто­му волна де Бройля ч-цы со спином аналогична волне с поляризацией: при данной частоте и длине волны она имеет 2J+1 поляризаций. Число поляризаций может быть произволь­ным целым числом, т. е. спиновое квант. число J может быть как целым (0,1,2,...), так и полуцелым (¹/₂, ³/₂, ⁵/₂,...) числом. Напр., спин эл-на, протона, нейтрона равен ¹/₂ (в еди­ницах ћ); спин ядер, состоящих из чётного числа нуклонов,— целый (или нулевой), а из нечётного — полу­целый. Отметим, что для фотона соот­ношение между числом поляризаций и спином (равным 1) другое: фотон не имеет массы покоя, а (как показывает релятив. К. м.) для таких ч-ц число

259


поляризаций равно двум (а не 2J+1=3).

Системы многих частиц. Тождествен­ные частицы. Квантовомеханич. ур-ние движения для системы, состоя­щей из N ч-ц, получается соответствую­щим обобщением ур-ния Шредингера для одной ч-цы. Оно содержит потенц. энергию, зависящую от коорди­нат всех ч-ц, и включает как воздей­ствие на них внеш. поля, так и вз-ствие ч-ц между собой. Волн. ф-ция также явл. ф-цией от координат всех ч-ц. Её можно рассматривать как волну в ЗN-мерном пр-ве; следовательно, на­глядная аналогия с распространением волн в обычном пр-ве утрачивается. Но теперь это несущественно, по­скольку известен смысл волн. ф-ции как амплитуды вероятности.

Если Квантовомеханич. системы со­стоят из одинаковых ч-ц, то в них на­блюдается специфич. явление, не имеющее аналогии в классич. меха­нике. В классич. механике случай одинаковых ч-ц тоже имеет нек-рую особенность. Пусть, напр., столкну­лись две одинаковые «классич.» ч-цы (первая двигалась слева, а вторая — справа) и после столкновения разле­телись в разные стороны (напр., пер­вая — вверх, вторая — вниз). Для результата столкновения не имеет



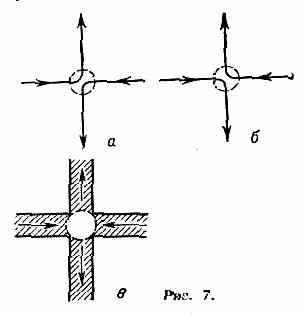
значения, какая из ч-ц пошла, напр., вверх, поскольку ч-цы одинаковы,— практически надо учесть обе возмож­ности (рис. 7, а и 7, б). Однако в прин­ципе в классич. механике можно различить эти два процесса, т. к. можно проследить за траекториями ч-ц во время столкновения. В К. м. траекторий, в строгом смысле этого слова, нет, и область столкновения обе ч-цы проходят с нек-рой неопре­делённостью, с «размытыми траекто­риями» (рис. 7, в). В процессе столкно­вения области размытия перекры­ваются, и невозможно даже в принци­пе различить эти два случая рассея­ния. Следовательно, одинаковые ч-цы становятся полностью неразличимы­ми — тождественными. Не имеет смысла говорить о двух разных случаях рассеяния, есть только один

случай — одна ч-ца пошла вверх, другая — вниз, индивидуальности у ч-ц нет. Этот квантовомеханич. прин­цип неразличимости одинаковых ч-ц можно сформулировать математически на языке волн. ф-ций. Нахождение ч-цы в данном месте пр-ва определя­ется квадратом модуля волн. ф-ции, зависящей от координат обеих ч-ц, |(l, 2)|², где 1 и 2 означают сово­купность координат и спин соотв. первой и второй ч-цы. Тождественность ч-ц требует, чтобы при перемене ме­стами ч-ц вероятности были одинако­выми, т. е.

|(1, 2)|²=|(2, 1)|². (23)

Отсюда вытекают две возможности:

(1, 2)=(2, 1), (24, а)

(1, 2) =-(2, 1). (24, б)

Если при перемене ч-ц местами волн. ф-ция не меняет знака, то она наз. симметричной [случай (24,а)], если меняет,— антисиммет­ричной [случай (24, б)]. Т. к. все вз-ствия одинаковых ч-ц симметричны относительно переменных 1, 2, то св-ва симметрии или антисимметрии волн. ф-ции сохраняются во времени.

В системе из произвольного числа тождеств. ч-ц должна иметь место симметрия или антисимметрия отно­сительно перестановки любой пары ч-ц. Поэтому св-во симметрии или антисимметрии — характерный при­знак данного сорта ч-ц. Соответствен­но, все ч-цы делятся на два класса: ч-цы с симметричными волн ф-циями наз. бозонами, с антисимметричными— фермионами. Существует связь между значением спина ч-ц и симметрией их волн. ф-ций: ч-цы с целым спином явл. бозонами, с полуцелым — фермионами (т. н. связь спина и статистики; см. ниже). Это правило сначала было установлено эмпирически, а затем доказано Паули теоретически (оно явл. одной из осн. теорем релятив. К. м.). В частности, эл-ны, протоны, нейтроны явл. фермионами, а фотоны, пи-мезоны, К-мезоны — бозонами. Сложные ч-цы (напр., ат. ядра), со­стоящие из нечётного числа фермионов, явл. фермионамн, а из чётного — бозонами.

Св-ва симметрии волн. ф-ции опре­деляют статистические св-ва системы. Пусть, напр., невзаимодействующие тождеств. ч-цы находятся в одинако­вых внеш. условиях (напр., во внеш. поле). Состояние такой системы можно определить, задав числа заполнения — числа ч-ц, находящихся в каждом данном (индивидуальном) состоянии, т. е. имеющих одинаковые наборы квант. чисел. Но если тождеств. ч-цы имеют одинаковые квант. числа, то их волн. ф-ция симметрична относитель­но перестановки ч-ц. Отсюда следует, что два одинаковых фермиона, входя­щих в одну систему, не могут нахо­диться в одинаковых состояниях, т. к. для фермионов волн. ф-ция должна быть антисимметричной. Это св-во

наз. принципом запрета Паули или Паули принципом. Т. о., числа запол­нения для фермионов могут прини­мать лишь значения 0 или 1. Т.к. эл-ны явл. фермионами, то принцип Паули существенно влияет на пове­дение эл-нов в атомах, в молекулах и т. д. Для бозонов же числа заполне­ния могут принимать произвольные целые значения. Поэтому с учетом квантовомеханич. св-в тождеств. ч-ц существует два типа статистик ч-ц: Ферми — Дирака статистика для фермионов и Бозе — Эйнштейна ста­тистика для бозонов. Пример систе­мы, состоящей из фермионов (ферми-системы),— электронный газ в метал­ле, пример бозе-системы — газ фотонов (т. е. равновесное эл.-магн. излуче­ние), жидкий ⁴Не.

Принцип Паули явл. определяющим для понимания структуры периодич. системы элементов Менделеева. В слож­ном атоме на каждом уровне энергии может находиться число эл-нов, рав­ное кратности вырождения этого уров­ня. Кратность вырождения зависит от орбит. квант. числа и от спина эл-на (s); она равна:

(2l+1)(2s+1)=2(2l+1).

Так возникает представление об элек­тронных оболочках атома, отвечаю­щих периодам в таблице элементов Менделеева (см. Атом).

Обменное взаимодействие. Химиче­ская связь. Молекула представляет собой связ. систему ядер и эл-нов, меж­ду к-рыми действуют электрические (кулоновскне) силы (притяжения и отталкивания). Т. к. ядра значитель­но тяжелее эл-нов, эл-ны движутся гораздо быстрее и образуют нек-рое распределение отрицат. заряда, в поле к-рого находятся ядра. В классич. механике и электростатике доказы­вается, что система такого типа не имеет устойчивого равновесия. По­этому, даже если принять устойчивость атомов (к-рую нельзя объяснить на основе законов классич. физики), не­возможно без специфически квантово­механич. закономерностей объяснить устойчивость молекул. Особенно непо­нятно с точки зрения классич. пред­ставлений существование молекул из одинаковых атомов, т. е. с ковалентной хим. связью (напр., простейшей молекулы — Н₂). Оказалось, что св-во антисимметрии электронной волн. ф-ции так изменяет хар-р вз-ст­вия эл-нов, находящихся у разных ядер, что возникновение такой связи становится возможным.

Рассмотрим для примера молекулу водорода Н₂, состоящую из двух протонов и двух эл-нов. Волн. ф-ция такой системы представляет собой произведение двух ф-ций, одна из к-рых зависит только от координат, а другая — только от спиновых пере­менных обоих эл-нов. Если суммарный спин эл-нов равен нулю (спины анти­параллельны), спиновая ф-ция анти­симметрична относительно нереста-

260


новки спиновых переменных эл-нов, и для того чтобы полная волн. ф-ция (в соответствии с принципом Паули) была антисимметричной, координат­ная часть волн. ф-ции _r должна быть симметричной относительно переста­новки координат эл-нов. Это озна­чает, что _r имеет вид:

_r~_a(1) _b(2)+_b(1) _a(2), (25) где _a(i), _b(i) — волн. ф-ции i-того эл-на (i=1,2) соотв. у ядра a и b.

Кулоновское вз-ствие пропорц. плотности электрич. заряда =e||²=е*. При учёте св-в симметрии e||², помимо плотности обычного вида:

e||(1)|²|2|_b(2)|², e|_b(1)|²|a(2)|², соответствующих движению отд. эл-нов у разных ядер, появляется плот­ность вида:

e*_a(1)*_b(2)_a(2),

e*_b(1)*_b(2)_a(2), e*_b(l)_a(l)*_a(2)_b(2).

Она паз. обменной плотно­стью, потому что возникает как бы за счёт обмена эл-нами между двумя атомами. Именно эта обменная плот­ность, приводящая к увеличению плот­ности отрицат. заряда между двумя положительно заряж. ядрами, и обе­спечивает устойчивость молекулы в случае ковалентной хим. связи. При суммарном спине эл-нов, равном еди­нице, _r антисимметрична, т. е. в (25) перед вторым слагаемым стоит знак минус, и обменная плотность имеет отрицат. знак, а следовательно, умень­шает плотность отрицат. электрич. заряда между ядрами, приводит как бы к дополнит. отталкиванию ядер. Т. о., симметрия волн. ф-ции приводит к «дополнительному», обменному вза­имодействию. Характерна зависи­мость этого вз-ствия от спинов эл-нов. Непосредственно динамически спины не участвуют во вз-ствии — источни­ком вз-ствия явл. электрич. силы, зависящие только от расстояния между зарядами, но в зависимости от ориен­тации спинов волн. ф-ция, антисим­метричная относительно перестановки двух эл-нов (вместе с их спинами), может быть симметричной или анти­симметричной относительно переста­новки только положения эл-нов (их координат). От типа же симметрии _r зависит знак обменной плотности и соотв. эфф. притяжение или отталки­вание ч-ц в результате обменного вз-ствия. Так, спины эл-нов благода­ря квантовомеханич. специфике св-в тождеств. ч-ц фактически определяют хим. связь. Расчёты строения и св-в молекул на основе К. м. явл. предме­том квантовой химии.

Обменное вз-ствие играет существ. роль во мн. явлениях, напр. объясняет ферромагнетизм. Множество явлений в конденсиров. телах тесно связано со статистикой образующих их ч-ц и с обменным вз-ствием. Условие антисим­метрии волн. ф-ции для фермионов приводит к тому, что они при большой плотности как бы эффективно отталки­ваются друг от друга, даже если между

ними не действуют никакие силы. В то же время между бозонами, к-рые описываются симметричными волн. ф-циями, возникают как бы силы притяжения: чем больше бозонов на­ходится в к.-л. состоянии, тем больше вероятность перехода др. бозонов системы в это состояние (подобного рода эффекты лежат в основе сверхте­кучести и сверхпроводимости, прин­ципа работы квант. генераторов и квант. усилителей).

Математическая схема квантовой ме­ханики. Нерелятив. К. м. может быть построена на основе немногих фор­мальных принципов. Матем. аппарат К. м. обладает логич. безупречностью и изяществом. Чёткие правила уста­навливают соотношение между эле­ментами матем. схемы и физ. величи­нами.

Первым осп. понятием К. м. явл. квантовое состояние. Вы­бор матем, аппарата К. м. диктуется физ. принципом суперпозиции квант. состояний, вытекающим из волн. св-в ч-ц. Согласно этому принципу, суперпозиция любых возможных со­стояний системы, взятых с произволь­ными (комплексными) коэффициента­ми, явл. также возможным состоя­нием системы. Объекты, для к-рых определены понятия сложения и умно­жения на комплексное число, наз. векторами. Т. о., принцип суперпо­зиции требует, чтобы состояние систе­мы описывалось нек-рым вектором — вектором состояния (с к-рым тесно связано понятие ампли­туды вероятности, или волн. ф-ции), являющимся элементом линейного «пр-ва состояний». Это позволяет ис­пользовать матем. аппарат, развитый для линейных (векторных) пр-в. Век­тор состояния обозначается, по Ди­раку, |>. Кроме сложения и умно­жения на комплексное число, вектор |> может подвергаться ещё двум операциям. Во-первых, его можно проектировать на другой вектор, т. е. составить скалярное произведение |> с любым другим вектором состоя­ния |'>; оно обозначается как <'|> и явл. комплексным числом, причём

<'|'<|'>*. (26)

Скалярное произведение вектора ||> с самим собой, <|>,— положит. число; оно определяет длину (норму) вектора. Длину вектора состояния удобно выбрать равной единице; его общий фазовый множитель произво­лен. Разл. состояния отличаются друг от друга направлением вектора состояния в пр-ве состояний.

Во-вторых, можно рассмотреть опе­рацию перехода от вектора |> к другому вектору |'> или произвести преобразование |>|'>. Симво­лически эту операцию можно записать как результат действия на |> нек-рого линейного оператора L:



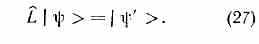
При этом |'> может отличаться от |> длиной и направлением. Линей­ные операторы, в силу принципа суперпозиции состояний, имеют в К.м. особое значение; в результате воздей­ствия линейного оператора на супер­позицию произвольных векторов |₁> и |₂> получается суперпозиция пре­образованных векторов:



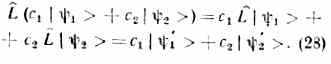
Важную роль для оператора L играют такие векторы |>|_>, для к-рых |'> совпадает по направ­лению с |>, т. е.



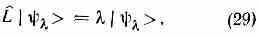
где  — число. Векторы |_ > наз. собственными векторами оператора L, а числа , — его собственными значениями. Собств. векторы |_> принято обозначать просто |>, т. е. |_>|>. Собств. значения  образуют либо дискр. ряд чисел (тогда говорят, что оператор L имеет дискр. спектр), либо непрерывный набор (непрерыв­ный спектр), либо частично дискрет­ный, частично непрерывный.

Очень важный для К. м. класс опе­раторов составляют линейные эрмитовы операторы, собств. значения  к-рых вещественны. Собств. векторы эрмитового опе­ратора, принадлежащие разл. собств. значениям, ортогональны друг к дру­гу, т. е.

<|'0. (30)

Из них можно построить ортогональ­ный базис («декартовы оси коорди­нат») в пр-ве состояний. Удобно нор­мировать эти базисные векторы на единицу: < |1. Произвольный вектор |> можно разложить по этому базису:



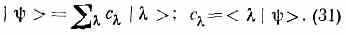
При этом:



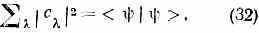
что эквивалентно теореме Пифагора; если |> нормирован на единицу, то



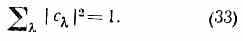
Принципиальное значение для по­строения матем. аппарата К. м. имеет тот факт, что для каждой физ. вели­чины существуют нек-рые выделен­ные состояния системы, в к-рых эта величина принимает вполне опреде­лённое (единств.) значение. По су­ществу это св-во явл. определением измеримой (физ.) величины, а со­стояния, в к-рых физ. величина имеет определ. значение, наз. собствен­ными состояниями этой, величины.

261


Согласно принципу суперпозиции, любое состояние системы может быть представлено в виде суперпозиции собств. состояний к.-л. физ. величины. Возможность такого представления математически аналогична возмож­ности разложения произвольного вектора по собств. векторам линейного эрмитового оператора. В соответствии с этим в К. м. каждой физ. величине, или наблюдаемой, L (координате, им­пульсу, моменту кол-ва движения, энергии и т. д.) ставится в соответст­вие линейный эрмитов оператор L. Собств. значения  оператора L интер­претируются как возможные значе­ния физ. величины L, получающиеся при измерениях. Если вектор состоя­ния |> — собств. вектор оператора L, то физ. величина L имеет определ. значение. В противном случае L при­нимает разл. значения  с вероятно­стью |с_|², где с_ — коэфф. разложе­ния |> по |>:

|_c_|>. (34)

Коэфф. c_=<|> разложения |> в базисе |> наз. также волн. ф-цией в -представлении. В частности, волн. ф-ция (х) представляет собой коэфф. разложения вектора состояния |> по собств. векторам оператора коорди­наты х:

(x)=
Ср. значение L наблюдаемой L в данном состоянии определяется коэфф. с_, согласно общему соотно­шению между вероятностью и ср. значением:



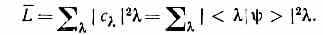
Значение L можно найти непосред­ственно через L и |> (без определе­ния коэфф. с_) по ф-ле:



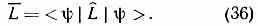
Вид линейных эрмитовых операто­ров, соответствующих таким физ. ве­личинам, как импульс, момент кол-ва движения, энергия, постулируется на основе общих принципов определения этих величин и соответствия принци­па, требующего, чтобы в пределе Ћ0 рассматриваемые физ. величины принимали «классич.» значения. Вме­сте с тем в К. м. вводятся нек-рые ли­нейные эрмитовы операторы [напр., отвечающие преобразованию векторов состояния при отражении осей коорди­нат (пространственной инверсии), пе­рестановке одинаковых ч-ц], к-рым соответствуют измеримые физ. вели­чины, не имеющие классич. аналогов (напр., чётность).

С операторами можно производить алгебр. действия сложения и умноже­ния. Но, в отличие от обычных чисел (к-рые в К. м. наз. с-числами), операторы явл. такими «числами» (q-числами), для к-рых операция умножения некоммутативна. Если L и М — два оператора, то в общем случае их дей­ствие на произвольный вектор |> в разл. порядке даёт разные векторы: LМ|>МL|>, т. е. LM ML. Величина LM-ML обозначается как [L, M] и наз. коммутатором. Только если два оператора переставимы (коммутируют), т. е. [L, М]=0, у них могут быть общие собств. векторы и, следовательно, наблюдаемые L и М могут одновременно иметь определён­ные (точные) значения  и . В оста­льных случаях эти величины не имеют одновременно определ. значений, и тогда они связаны соотношением не­определённостей. Можно показать, что если [L, М]=с, то LM|c|/2, где L и M — среднеквадратичные отклонения от ср. значений для соот­ветствующих величин.

Возможна такая матем. формулиров­ка, в к-рой формальный переход от классич. механики к К. м. осуществ­ляется заменой с-чисел соответствую­щими q-числами. Сохраняются и ур-ния движения, но они превращаются в уравнения для операторов. Из этой формальной аналогии между К. м. и классич. механикой можно найти осн. коммутационные (перестановоч­ные) соотношения. Так, для коорди­наты и импульса [х, p]=iћ. Отсюда следует соотношение неопределён­ностей рхћ/2. Из перестановочных соотношений можно получить, в частности, явный вид оператора им­пульса в координатном представле­нии. Тогда волн. ф-ция есть (x), a оператор импульса — дифф. оператор



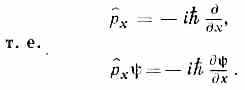
Можно показать, что спектр его собств значений непрерывен, а амплитуда вероятности есть де-бройлевская волна (|р> — собств. вектор опе­ратора импульса р). Если задана энер­гия системы Н(р, х) как ф-цня коор­динат и импульсов ч-ц, то знание ком­мутатора [х, р] достаточно для на­хождения [Н, р], [Н, х], а также уровней энергии как собств. значений оператора полной энергии Н.

На основании определения момента кол-ва движения M_z=xp_y- ур_х,...

можно получить, что |М_x, М_y|=iћM_z. Эти коммутац. соотношения справед­ливы и при учёте спинов ч-ц; оказы­вается, что они достаточны для определения собств. значения квадра­та полного момента: M²=Ћ²j (j+1), где квант. число j — целое или полу­целое число, и его проекции:

M_z=mћ, m=-j,-j+1,...,+j. Ур-ния движения квантовомеханич. системы могут быть записаны в двух

формах: в виде ур-ния для вектора состояния



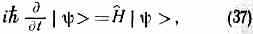
наз. шрёдингеровской формой ур-ния движения, и в виде ур-ния для опе­раторов (q-чисел)



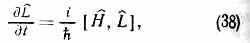
наз. гейзенберговской формой ур-ний движения (наиб. близкой классич. механике). Из (38), в частности, сле­дует, что ср. значения физ. величин изменяются по законам классич. механики; это положение наз. тео­ремой Эренфеста.

Для логич. структуры К. м. харак­терно присутствие двух разнородных по своей природе составляющих. Вектор состояния (волн. ф-ция) одно­значно определён в любой момент времени, если задан в нач. момент при известном вз-ствии системы. В этой части теория вполне детерминистична. Но вектор состояния не есть наблюдаемая величина. О наблюдае­мых на основе знания |> можно сде­лать лишь статистические (вероятно­стные) предсказания. Результаты индивидуального измерения над квант. объектом в общем случае непредска­зуемы. Предпринимались попытки восстановить идею полного детерми­низма в классич. смысле введением предположения о неполноте квантовомеханнч. описания. Напр., высказы­валась гипотеза о наличии у квант. объектов дополнит. степеней свободы — «скрытых параметров», учёт к-рых сделал бы поведение системы полно­стью детерминированным в смысле классич. механики; неопределённость возникает только вследствие того, что эти «скрытые параметры» неизвестны и не учитываются. Однако амер. учёный Дж. фон Нейман доказал теорему о невозможности нестатистич. интерпретации К. м. при сохранении её осн. положения о соответствии между наблюдаемыми (физ. величи­нами) и операторами.

• Классич. труды — Гейзенберг В., Физические принципы квантовой теории, Л.—М., 1932; Дирак П., Принципы кван­товой механики, пер. с англ., М., 1960; Паули В., Общие принципы волновой ме­ханики, пер. с нем., М.—Л., 1947. Учебни­ки — Ландау Л. Д., Л и ф ш и ц Е. М., Квантовая механика. Нерелятивистская тео­рия, 3 изд., М., 1974 (Теоретическая физи­ка, т. 3); Б л о х и н ц е в Д. И., Основы квантовой механики, 4 изд., М., 1963; Д а в ы д о в А. С., Квантовая механика, М., 1963; Ф е й н м а н Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, пер. с англ., в. 8—9, М., 1966—67; Ш и ф ф Л., Квантовая механика, пер. с англ., 2 изд., М., 1959; М е с с и а А., Квантовая механи­ка, пер. с франц., т. 1—2, М., 1978—79.

В. Б. Берестецкий.