От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Квантовая механика История создания К. м. Дифракция микрочастиц). Вероятности и волны.

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КВАНТОВАЯ МЕХАНИКА (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч-ц, атомов, моле­кул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч-цы и системы, с физ. величинами, непосредственно из­меряемыми на опыте.

Законы К. м. составляют фунда­мент изучения строения в-ва. Они позволили выяснить строение атомов, установить природу хим. связи, объ­яснить периодич. систему элементов, понять строение ат. ядер, изучать св-ва элем. ч-ц. Поскольку св-ва мак­роскопич. тел определяются движе­нием и вз-ствием ч-ц, из к-рых они состоят, законы К. м. лежат в основе понимания большинства макроскопич. явлений. К. м. позволила, напр., объ­яснить температурную зависимость теплоёмкостей газов и тв. тел и вычис­лить их величину, определить строе­ние и понять мн. св-ва тв. тел (метал­лов, диэлектриков, ПП). Только на основе К. м. удалось последовательно объяснить такие явления, как фер­ромагнетизм, сверхтекучесть, сверх­проводимость, понять природу таких астрофиз. объектов, как белые кар­лики, нейтронные звёзды, выяснить механизм протекания термоядерных реакций в Солнце и звёздах. Сущест­вуют также явления (напр., Джозефсона эффект), в к-рых законы К. м. непосредственно проявляются в пове­дении макроскопич. объектов.

Ряд крупнейших техн. достижений 20 в. основан по существу на специфич. законах К. м. Так, квантовомеханич. законы лежат в основе работы яд.

реакторов, обусловливают возмож­ность осуществления в земных усло­виях термояд. реакций, проявляются в ряде явлений в металлах и ПП, используемых в новейшей технике, и т. д. Фундамент квантовой электро­ники составляет квантовомеханич. теория излучения. Законы К. м. ис­пользуются при целенаправл. поиске и создании новых материалов (особен­но магнитных, полупроводниковых и сверхпроводящих). Т. о., К. м. стала в значит. мере «инженерной» наукой, знание к-рой необходимо не только физикам-исследователям, но и ин­женерам.

Место К. м. среди других наук о дви­жении. В нач. 20 в. выяснилось, что классич. механика Ньютона имеет огранич. область применимости и нуж­дается в обобщении. Во-первых, она неприменима при скоростях движения тел, сравнимых со скоростью света. Здесь её заменила релятив. механика, построенная на основе спец. теории относительности Эйнштейна (см. Относительности теория). Релятив. ме­ханика включает в себя Ньютонову (нерелятивистскую) механику как частный случай. (Ниже термин «клас­сич. механика» будет объединять Нью­тонову и релятив. механику.)

Для классич. механики в целом ха­рактерно описание ч-ц путём задания их положения в пр-ве (координат) и скоростей и зависимости этих величин от времени. Такому описанию соот­ветствует движение ч-ц но вполне определ. траекториям. Однако опыт показал, что это описание не всегда справедливо, особенно для ч-ц с очень малой массой (микрочастиц). В этом состоит второе ограничение примени­мости механики Ньютона. Более об­щее описание движения даёт К. м., к-рая включает в себя, как частный случай, классич. механику. К. м. де­лится на нерелятивистскую, справед­ливую в случае малых скоростей, и релятивистскую, удовлетворяющую требованиям спец. теории относитель­ности. В статье изложены основы нерелятив. К. м. (однако нек-рые общие положения относятся к квант. теории в целом). Нерелятив. К. м. (как и механика Ньютона для своей области применимости) — вполне за­конченная и логически непротиворе­чивая теория, способная в области своей компетентности количественно решать в принципе любую физ. задачу. Релятив. К. м. не явл. в такой сте­пени завершённой и свободной от противоречий теорией. Если в нере­лятив. области можно считать, что движение определяется силами, дей­ствующими (мгновенно) на расстоя­нии, то в релятив. области это не­справедливо. Поскольку, согласно теории относительности, вз-ствие пере­даётся (распространяется) с кон. ско­ростью, должен существовать физ. агент, переносящий вз-ствие; таким агентом явл. физ. поле. Трудности ре­лятив. теории — это трудности теории

252


поля, с к-рыми встречается как релятив. классич. механика, так и релятив. К. м. В статье не будут рассматриваться вопросы релятив. К. м., связанные с квантовой теорией поля.

Соотношение между классической и К. м. определяется существованием универсальной мировой постоянной— постоянной Планка h (или h=h/2). Постоянная h, наз. также квантом действия, имеет размерность дей­ствия и равна: h6,62•10^-27 эрг•с h=1,05•10^-27 эрг•с). Если в услови­ях данной задачи физ. величины раз­мерности действия значительно боль­ше h (так что h можно считать очень малой величиной), применима клас­сич. механика. Формально это усло­вие и явл. критерием применимости классической механики. Более под­робно этот критерий будет разъяс­нён при изложении физических основ К. м.

История создания К. м. В нач. 20 в. были обнаружены две (казалось, не связанные между собой) группы явле­ний, свидетельствующих о неприме­нимости механики Ньютона и клас­сич. электродинамики к процессам вз-ствия света с в-вом и к процессам, происходящим в атоме. Первая группа явлений была связана с установле­нием на опыте двойственной природы света — дуализмом света (см. ниже); вторая — с невозможно­стью объяснить на основе классич. представлений существование устой­чивых атомов, а также их оптич. спектры. Установление связи между этими группами явлений и попытки объяснить их на основе новой теории и привели, в конечном счёте, к открытию законов К. ж.

Впервые квант. представления (в т. ч. h) были введены в 1900 нем. физиком М. Планком в работе, посвя­щённой теории теплового излучения тел (см. Планка закон излучения). Существовавшая к тому времени теория теплового излучения, построенная на основе классич. электродинамики и статистич. физики, приводила к бессмысленному результату, состояв­шему в том, что тепловое (термодинамич.) равновесие между излучением и в-вом не может быть достигнуто, т. к. вся энергия должна перейти в излу­чение. Планк разрешил это противо­речие и получил результаты, прекрас­но согласующиеся с опытом, предпо­ложив, что свет испускается не непре­рывно (как это следовало из классич. теории излучения), а определёнными дискр. порциями энергии — кван­тами. Величина такого кванта энер­гии зависит от частоты света v и равна: ξ=h.

От этой работы Планка можно про­следить две взаимосвязанные линии развития, завершившиеся к 1927 окон­чат. формулировкой К. м. в двух её формах. Первая начинается с работы Эйнштейна (1905), в к-рой была дана теория фотоэффекта. Развивая идею

Планка, Эйнштейн предположил, что свет не только испускается и погло­щается, но и распространяется кван­тами, т. е. что дискретность присуща самому свету: свет состоит из отд. пор­ций — световых квантов, названных позднее фотонами. Энергия фотона ξ=h. На основании этой гипотезы Эйнштейн объяснил установленные на опыте закономерности фотоэффекта, к-рые противоречили классической (ба­зирующейся на классич. электродина­мике) теории света.

Дальнейшее доказательство корпус­кулярного хар-ра света было получено в 1922 амер. физиком А. Комптоном, показавшим экспериментально, что рассеяние света свободными эл-нами происходит по законам упругого стол­кновения двух ч-ц — фотона и эл-на (см. Комптона эффект). Кинематика такого столкновения определяется за­конами сохранения энергии и импуль­са, причём фотону наряду с энергией ξ=h следует приписать импульс p=h/= h/c, где  — длина световой волны. Энергия и импульс фотона связаны соотношением ξ=ср, спра­ведливым в релятив. механике для ч-цы с нулевой массой покоя. Т. о., было доказано экспериментально, что наряду с известными волн. св-вами (проявляющимися, напр., в дифрак­ции света) свет обладает и корпуску­лярными св-вами: он состоит как бы из ч-ц — фотонов. В этом проявляется дуализм света, его корпускулярно-волн. природа. Дуализм содержится уже в ф-ле ξ=h, не позволяющей выбрать к.-л. одну из двух концеп­ций: энергия ξ относится к ч-це, а частота  явл. хар-кой волны. Воз­никло формальное логич. противоре­чие: для объяснения одних явлений необходимо было считать, что свет имеет волн. природу, а для объясне­ния других — корпускулярную. По существу разрешение этого противо­речия и привело к созданию физ. основ К. м.

В 1924 франц. физик Л: де Бройль, пытаясь найти объяснение постулиро­ванным в 1913 дат. физиком Н. Бо­ром условиям квантования ат. орбит (см. ниже), выдвинул гипотезу о всеобщности корпускулярно-волнового дуализма. Согласно де Бройлю, каж­дой ч-це, независимо от её природы, следует поставить в соответствие вол­ну, длина к-рой  связана с импуль­сом ч-цы р соотношением:

=h/p. (1)

По этой гипотезе не только фотоны, но и все «обыкновенные ч-цы» (эл-ны, протоны и др.) обладают волн. св-ва ми, к-рые, в частности, должны про­являться в дифракции ч-ц. В 1927 амер. физики К. Дэвиссон и Л. Джермер впервые наблюдали дифракцию эл-нов. Позднее волн. св-ва были обнаружены и у др. ч-ц, и справед­ливость ф-лы де Бройля была под­тверждена экспериментально (см.

Дифракция микрочастиц). В 1926 австр. физик Э. Шредингер пред­ложил ур-ние, описывающее пове­дение таких «волн» во внеш. силовых полях. Так возникла волновая механика. Волн. ур-ние Шре­дингера явл. основным ур-нием нерелятив. К. м. В 1928 англ. физик П. Дирак сформулировал релятив. ур-ние, описывающее движение эл-на во внеш. силовом поле; Дирака урав­нение стало одним из осн. ур-ний ре­лятив. К. м.

Вторая линия развития (также яв­ляющаяся обобщением гипотезы План­ка) начинается с работы Эйнштейна (1907), посвящённой теории теплоём­кости тв. тел. Эл.-магн. излучение, представляющее собой набор эл.-магн. волн разл. частот, динамически экви­валентно нек-рому набору осциллято­ров. Испускание или поглощение волн эквивалентно возбуждению или зату­ханию соответствующих осцилляторов. Тот факт, что испускание и поглоще­ние эл.-магн. излучения в-вом про­исходят квантами с энергией h, можно выразить так: осциллятор поля не может обладать произвольной энер­гией, он может иметь только определ. значения энергии — дискр. уровни энергии, расстояние между к-рыми равно h. Эйнштейн обобщил идею квантования энергии осциллятора эл.-магн. поля на осциллятор произ­вольной природы. Поскольку тепло­вое движение тв. тел сводится к коле­баниям атомов, то и тв. тело динами­чески эквивалентно набору осцилля­торов. Энергия таких осцилляторов тоже квантованна, т. е. разность со­седних уровней энергии должна рав­няться h, где  — частота колебаний атомов. Теория Эйнштейна, уточнён­ная П. Дебаем, М. Борном и Т. Кар­маном (Германия), сыграла выдаю­щуюся роль в развитии теории тв. тел.

В 1913 Бор применил идею кванто­вания энергии к теории строения ато­ма, планетарная модель к-рого выте­кала из результатов опытов англ. фи­зика Э. Резерфорда (1911). Согласно этой модели, в центре атома находится положительно заряж. ядро, в к-ром сосредоточена почти вся масса атома; вокруг ядра вращаются по орбитам отрицательно заряж. эл-ны. Рассмот­рение такого движения на основе клас­сич. представлений приводило к па­радоксальному результату — невоз­можности существования стабильных атомов: согласно классич. электроди­намике, эл-н не может устойчиво двигаться по орбите, поскольку вра­щающийся электрич. заряд должен излучать эл.-магн. волны и, следова­тельно, терять энергию; радиус его орбиты должен непрерывно уменьша­ться, и за время ~ 10^-8 с эл-н должен упасть на ядро. Это означало, что законы классич. физики неприменимы

253


к движению эл-нов в атоме, т. к. ато­мы не только существуют, но и весьма устойчивы.

Для объяснения устойчивости ато­мов Бор предположил, что из всех орбит, допускаемых Ньютоновой ме­ханикой для движения эл-на в электрич. поле ат. ядра, реально осуществ­ляются лишь те, к-рые удовлетворяют определ. условиям квантования, тре­бующим, чтобы величина действия для классич. орбиты была целым кратным постоянной Планка h. Бор постулиро­вал, что, совершая допускаемое усло­виями квантования орбит. движение (т. е. находясь на определ. уровне энергии), эл-н не испускает световых волн. Излучение происходит лишь при переходе эл-на с одной орбиты на другую, т. е. с одного уровня энергии ξ_i на другой, с меньшей энергией ξ_k при этом рождается квант света с энергией

h=ξ_i-ξ_k. (2)

Так возникает линейчатый спектр ато­ма. Бор получил правильную ф-лу для частот спектр. линий атома во­дорода (и водородоподобных атомов), охватывающую совокупность откры­тых ранее эмпирич. ф-л (см. Спектра­льные серии). Существование уровней энергии в атомах было непосредст­венно подтверждено Франка — Герца опытами (1913—14).

Т. о., Бор, используя квант. посто­янную h, отражающую дуализм света, показал, что эта величина определяет также и движение эл-нов в атоме, законы к-рого существенно отличаются от законов классич. механики. Этот факт позднее был объяснён на основе универсальности корпускулярно-волн. дуализма.

Успех теории Бора, как и предыду­щие успехи квант. теории, был до­стигнут за счёт нарушения логич. цельности теории: с одной стороны, использовалась Ньютонова механика, с другой — привлекались чуждые ей искусств. правила квантования, к тому же противоречащие классич. электродинамике. Кроме того, теория Бора оказалась не в состоянии объяс­нить движение эл-нов в сложных атомах (даже в атоме гелия), возник­новение связи между атомами, приво­дящей к образованию молекулы, и др. «Полуклассич.» теория Бора не могла также ответить на вопрос, как движет­ся эл-н при переходе с одного уровня энергии на другой. Дальнейшая раз­работка вопросов теории атома при­вела к убеждению, что движение эл-нов в атоме нельзя описывать в тер­минах (понятиях) классич. механи­ки (как движение по определ. траек­тории, или орбите), что вопрос о дви­жении эл-на между уровнями не­совместим с хар-ром законов, опреде­ляющих поведение эл-нов в атоме, и что необходима новая теория, в

к-рую входили бы только величины, относящиеся к начальному и конечно­му стационарным состояниям атома. В 1925 нем. физик В. Гейзенберг построил такую формальную схему, в к-рой вместо координат и скоростей эл-на фигурировали некие абстракт­ные алгебр. величины — матрицы; связь матриц с наблюдаемыми вели­чинами (уровнями энергии и интенсивностями квант. переходов) дава­лась простыми непротиворечивыми правилами. Работа Гейзенберга была развита Борном и П. Иорданом (Герма­ния). Так возникла матричная механика. Вскоре после появле­ния ур-ния Шредингера была показа­на матем. эквивалентность волновой (основанной на ур-нии Шредингера) и матричной механики. В 1926 Борн дал вероятностную интерпретацию волн де Бройля (см. ниже).

Большую роль в создании К. м. сыграли работы Дирака, относящиеся к этому же времени. Окончат. форми­рование К. м. как последоват. теории с ясными физ. основами и стройным матем. аппаратом произошло после работы Гейзенберга (1927), в к-рой было сформулировано неопределённос­тей соотношение — важнейшее соотно­шение, освещающее физ. смысл ур-ний К. м., её связь с классич. механи­кой и другие как принципиальные вопросы, так и качеств. результаты К. м. Эта работа была продолжена и обобщена в трудах Бора и Гейзенбер­га.

Детальный анализ спектров атомов привёл к представлению (введённому впервые амер. физиками Дж. Ю. Уленбеком и С. Гаудсмитом и развитому швейц. физиком В. Паули) о том, что эл-ну, кроме заряда и массы, должна быть приписана ещё одна внутр. хар-ка — спин. Важную роль сыграл открытый Паули (1925) т. н. прин­цип запрета (Паули принцип, см. ниже), имеющий фундам. значение в теории атома, молекулы, ядра, тв. тела.

В течение короткого времени К. м. была с успехом применена к широкому кругу явлений. Были созданы те­ории ат. спектров, строения молекул, хим. связи, периодич. системы эле­ментов, металлич. проводимости и ферромагнетизма. Дальнейшее прин­ципиальное развитие квант. теории связано гл. обр. с релятив. К. м. Нерелятив. К. м. развивалась в осн. в направлении охвата разнообразных конкретных задач физики атомов, мо­лекул, тв. тел (металлов, ПП), плазмы и т. д., а также совершенствования матем. аппарата и разработки коли­честв. методов решения разл. задач.

Вероятности и волны. Законы К. м. не обладают той степенью наглядности, к-рая свойственна законам классич. механики. Поэтому целесообразно про­следить линию развития идей, состав­ляющих фундамент К. м., и только после этого сформулировать её осн. положения. Выбор фактов, на базе

к-рых строится теория, не единствен, поскольку К. м. описывает широчай­ший круг явлений и каждое из них способно дать материал для её обос­нования.

Рассмотрим простейший опыт по распространению света (рис. 1). На пути пучка света ставится прозрачная пластинка S. Часть света проходит через пластинку, часть отражается от неё. Известно, что свет состоит из «ч-ц» — фотонов. Что же происходит



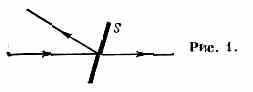
с отдельным фотоном при попадании его на пластинку? Если поставить опыт (напр., с пучком света крайне малой интенсивности), в к-ром можно следить за судьбой каждого фотона, то можно убедиться, что при встрече с пластинкой фотон не рас­щепляется на два, его индивидуаль­ность как ч-цы сохраняется (иначе свет менял бы свою частоту). Оказы­вается, что нек-рые фотоны проходят сквозь пластинку, а нек-рые отража­ются от неё. Если поместить такую же пластинку на пути прошедшего (или отражённого) света, то будет наблю­даться та же картина: часть фотонов пройдёт вторую пластинку, часть от­разится. Следовательно, одинако­вые ч-цы в одинаковых усло­виях могут вести себя по-разному, т. е. поведение фотона при встрече с пластинкой не предска­зуемо однозначно. Детерми­низма в том смысле, как это понима­ется в классич. механике, при движе­нии фотонов не существует. Этот вы­вод явл. одним из отправных пунктов для устранения противоречия между корпускулярными и волн. св-вами ч-ц и построения теории квантовомеханич. явлений.

Волн. теория легко объясняет от­ражение света от прозрачной пластин­ки и прохождение через неё, однознач­но предсказывая отношение интенсивностей прошедшего и отражённого света. С корпускулярной точки зрения интенсивность света пропорц. числу фотонов, следовательно, волн. оптика позволяет определить отношение чи­сел прошедших (n₁) и отражённых (N₂) фотонов, N₁/N₂(N₁+N₂)=N—полное число падающих на пластинку фотонов). Поведение же одного фотона, естественно, ею не описы­вается. Отражение фотона от пластин­ки или прохождение через неё — слу­чайные события: нек-рые фотоны про­ходят через пластинку, нек-рые отра­жаются от неё, но при большом N отношение N₁/N₂ находится в согла­сии с предсказанием волн. оптики. Количественно закономерности, про­являющиеся при случайных событиях, описываются с помощью теории веро­ятностей. Фотон может с вероятно­стью w₁ пройти через пластинку и с

254


вероятностью w₂ отразиться от неё, так что в ср. пройдёт пластинку w₁N ч-ц, а отразится w₂N ч-ц. Если N очень велико, то средние (ожидаемые) значения чисел ч-ц точно совпадают с истинными. Все соотношения оптики могут быть переведены с языка интенсивностей на язык вероятностей, и тогда они будут относиться к поведе­нию одного фотона. Вероятность того, что с фотоном произойдёт одно из двух альтернативных (взаимоисклю­чающих) событий — прохождение или отражение, равна w₁+w₂=1. Это за­кон сложения вероятнос­тей, соответствующий сложению интенсивностей. Вероятность прохождения через две одинаковые пластинки равна w²₁, а вероятность прохождения через первую и отраже­ния от второй — w₁w₂ (что соответ­ствует разделению света второй пла­стинкой на прошедший и отражённый в том же отношении, что и первой). Это закон умножения вероятностей, справедливый для независимых событий. Аналогичные опыты с пучком эл-нов или др. микро­частиц также показывают непредска­зуемость поведения отд. ч-цы. Однако не только прямые опыты говорят в пользу того, что и в самом общем слу­чае следует перейти к вероятностному описанию поведения микрочастиц. Теоретически невозможно предста­вить, что одни микрочастицы описы­ваются вероятностно, а другие клас­сически: вз-ствие «классич.» ч-ц с «квантовыми» с необходимостью при­водило бы к внесению квант. неопре­делённостей и делало бы поведение «классич.» ч-ц также непредсказуе­мым (в смысле классич. детерминиз­ма). Т. о., возможная формулировка задачи К. м.— предсказание вероят­ностей разл. процессов (в отличие от классич. механики, предсказывающей

в принципе достоверные события). Вероятностное описание возможно и в классич. механике: когда нач. ус­ловия заданы не точно, а с нек-рой степенью неопределённости, то и пред­сказания будут содержать неопреде­лённости, т. е. носить в той или иной степени вероятностный хар-р. Приме­ром служит классич. статистич. физи­ка, оперирующая с усреднёнными ве­личинами. Поэтому дистанция между строем мысли квант. и классич. меха­ники была бы не столь велика, если бы осн. понятиями К. м. были именно вероятности. Чтобы выяснить ради­кальное различие между К. м. и клас­сич. механикой, усложним рассмотрен­ный выше опыт по отражению света. Пусть отражённый пучок света (или микрочастиц) при помощи зеркала 3



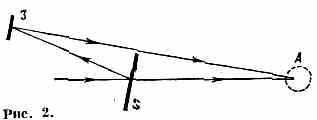
(рис. 2) меняет направление и попа­дает в ту же область А (напр., в тот же детектор, регистрирующий фото­ны), что и прошедший пучок. Есте­ственно было бы ожидать, что в этом случае измеренная интенсивность равна сумме интенсивностей прошед­шего и отражённого пучков. Однако известно, что в результате интерфе­ренции света интенсивность в зависи­мости от расположения зеркала и детектора может меняться в довольно широких пределах и даже обращаться в ноль (пучки как бы гасят друг друга). Что же можно сказать о поведении отд. фотона в пнтерференц. опыте? Вероятность его попадания в данный детектор существенно перераспреде­лится по сравнению с первым опытом (рис. 1) и не будет равна сумме веро­ятностей прихода фотона в детектор первым и вторым путями, т. е. эти два пути не явл. альтернативными. Т. о., наличие двух возможных пу­тей прихода фотона от источника к детектору существ. образом влияет на распределение вероятностей, и поэто­му нельзя сказать, каким путём про­шёл фотон от источника к детектору. Приходится считать, что он одновре­менно мог прийти двумя разл. путями. Аналогичный опыт, проведённый с пучками др. микрочастиц, даёт тот же результат. Возникающие представле­ния действительно радикально отли­чаются от классических: невозможно представить себе движение ч-цы одно­временно по двум путям. Но К. м. и не ставит такой задачи. Она лишь предсказывает результаты опытов с пучками ч-ц. Подчеркнём, что в дан­ном случае не высказывается никаких гипотез, а даётся лишь интерпрета­ция волн. опыта с точки зрения кор­пускулярных представлений. Полу­ченный результат означает невозмож­ность классич. описания движения ч-ц по траекториям, отсутствие наг­лядности квант. описания.

Попытаемся всё же выяснить, ка­ким путём прошла ч-ца, поставив на возможных её путях детекторы. Есте­ственно, что ч-ца будет зарегистриро­вана в к.-л. одном детекторе. Но как только измерение выделит определ. траекторию ч-цы, интерференц. кар­тина исчезнет. Распределение вероят­ностей станет другим. Для возник­новения интерференции нужны обе (все) возможные траектории. Т. о., регистрация траектории ч-цы так изме­няет условия, что два пути становятся альтернативными, и в результате по­лучается сложение интенсивностей (или вероятностей), к-рое было бы в случае «классич.» ч-ц, движущихся по определ. траекториям.

Для квант. явлений очень важно точное описание условий опыта, в к-рых наблюдается данное явление. В условия, в частности, входят и из­мерит. приборы. В классич. физике предполагается, что состояние систе­мы при измерении не меняется. В квант. физике такое предположение

несправедливо: измерит. прибор сам участвует в формировании изучаемого на опыте явления, и эту его роль нель­зя не учитывать. Роль измерит. при­бора в квант. явлениях была всесто­ронне проанализирована Бором и Гейзенбергом. Она тесно связана с соот­ношением неопределённостей (см. ниже).

Внимание к роли измерений не оз­начает, что в К. м. не изучаются физ. явления безотносительно к приборам, напр. св-ва ч-ц «самих по себе». При­мерами могут служить решаемые К. м. задачи об уровнях энергии атомов, о рассеянии микрочастиц при их столкновениях, об интерференц. яв­лениях. Роль прибора выступает на первое место тогда, когда ставятся специфич. вопросы, лишённые, как выяснилось, смысла, напр. вопрос о том, по какой траектории двигался эл-н в интерференц. опыте (т. к. либо нет траектории, либо нет интерферен­ции) .

Интерференц. опыт, как и опыт по отражению света, легко объясняется на основе волн. оптики. В оптике каждая волна характеризуется не только интенсивностью I или амплиту­дой А (I ~ А²), но и фазой . Сово­купность действит. величин А и  принято объединять в одно комплекс­ное число — комплексную амплитуду: =Ae^i. Тогда I=||²=•=A², где

* — ф-ция, комплексно сопряжён­ная с . Т..к. непосредственно изме­ряется именно интенсивность, то для одной волны фаза не проявляется. В опыте с прохождением и отражением света (рис. 1) ситуация именно такая: имеются две волны с комплексными амплитудами ₁ и ₂, но одна из них существует только справа, а другая только слева от пластинки; интенсив­ности этих волн I₁=A²₁, I₂=A²₂, т. е.

фазы не фигурируют. В интерференц. опыте (рис. 2) ситуация иная: волна с амплитудой ₂ с помощью зеркала попадает в область нахождения волны с амплитудой ₁. Волн. поле в обла­сти существования двух волн опреде­ляется с помощью принципа суперпо­зиции: волны складываются с учётом их фаз. Амплитуда суммарной волны

 равна сумме комплексных амплитуд обеих волн:

=₁+₂=A₁е^i1+A₂е^i2. (3)

Интенсивность суммарной волны за­висит от разности фаз ₁-₂ (к-рая пропорц. разности хода световых пучков по двум путям):

||² = |А₁е^i2+A₂е^i2|²=A²₁+A²₂+ 2A₁A₂cos(₁-₂). (4)

Если А₁=А₂ и cos(₁-₂)=-1, то ||²=0. В более общем случае из-за изменения условий опыта (напр., св-в зеркала) амплитуды могут изме­няться по величине и фазе, так что

255


комплексной амплитудой суммарной волны будет =c₁₁+с₂₂, где c₁ и с₂ — комплексные числа. Суть явле­ния при этом остаётся прежней. Хар-р явления не зависит также от общей интенсивности. Если увеличить  в С раз (С может быть как комплекс­ным, так и действительным), то интен­сивность увеличится в |С|² раз, т. е. |С|² будет общим множителем в ф-ле распределения интенсивностей.

Для интерпретации волн. явлений с корпускулярной точки зрения необ­ходимо перенесение принципа супер­позиции в К. м. Поскольку К. м. име­ет дело не с интенсивностями, а с вероятностями, следует ввести амплитуду вероятности =Ae^i, полагая (по аналогии с оптич. волнами), что вероятность w=|C|²=|C|²*. Здесь С — число, наз. нормировочным множителем, к-рый должен быть подобран так, чтобы суммарная вероятность обна­ружения ч-цы во всех возможных местах равнялась единице, т.е. _iw_i=1. Множитель С определён только по модулю, фаза его произвольна. Нор­мировочный множитель важен только для определения абс. вероятности; относит. вероятности определяются ам­плитудами вероятности в произволь­ной нормировке. Амплитуда вероят­ности наз. в К. м. волновой функцией. Амплитуды вероятности, как и оптич. амплитуды, удовлетворяют принципу суперпозиции: если ₁ и ₂ — амп­литуды вероятности прохождения ч-цы соотв. первым и вторым путём, то амплитуда вероятности для случая, когда осуществляются оба пути, должна быть равна: =₁+₂. Тем самым фраза: «Ч-ца прошла двумя пу­тями», приобретает волн. смысл, а ве­роятность w=|₁+₂|² обнаруживает интерференц. св-ва.

Следует подчеркнуть, что смысл, вкладываемый в понятие суперпози­ции в оптике (и др. волн. процессах) и в К. м., различен. Сложение (су­перпозиция) обычных волн не проти­воречит наглядным представлениям, т. к. каждая из волн представляет возможный тип колебаний и суперпо­зиция соответствует сложению этих колебаний в каждой точке. Квантово-механические же амплитуды вероят­ности описывают альтернативные, с классич. точки зрения исключаю­щие друг друга движения (напр., волны ₁ и ₂ соответствуют ч-цам, приходящим в детектор двумя разл. путями). Сложение таких движений совершенно непонятно с позиции классич. физики. В этом проявляется отсутствие наглядности квантовомеханич. принципа суперпозиции. Избе­жать формального логич. противоре­чия этого принципа в К. м. (возмож­ность для ч-цы пройти одновременно двумя путями) позволяет вероятност­ная интерпретация. Постановка опыта

по определению пути ч-цы приведет к тому, что с вероятностью |₁|² ч-ца пройдёт первым и с вероятностью |₂|² — вторым путём; суммарное рас­пределение ч-ц на экране будет опре­деляться вероятностью |₁|²+|²l'², т. е. интерференция исчезнет.

Т. о., рассмотрение интерференц. опыта приводит к след. выводам. Ве­личиной, описывающей состояние физ. системы в К. м., явл. амплитуда ве­роятности, или волн. ф-ция системы; осн. черта такого квантовомеханич. описания — предположение о спра­ведливости принципа суперпо­зиции состояний.

В общем виде принцип суперпозиции утверждает, что если в данных усло­виях возможны разл. квант. состоя­ния ч-цы (или системы ч-ц), к-рым соответствуют волн. ф-ции ₁, ₂,..., _i..., то существует и состояние, опи­сываемое волн. ф-цией _ic_i_i, где c_i — произвольные комплексные числа. Если _i описывают альтернативные состояния, то |c_i|² определяет вероятность того, что система находит­ся в состоянии с волн. ф-цией _i и

|c_i|²=1.

Волны де Бройля и соотношение неопределённостей. Одна из осн. задач К. м.— нахождение волн. ф-ции, от­вечающей данному состоянию изу­чаемой системы. Рассмотрим решение этой задачи на простейшем (но важ­ном) случае свободно движущейся ч-цы. Согласно де Бройлю, со свобод­ной ч-цей, имеющей импульс р, свя­зана волна с длиной =h/p. Это озна­чает, что волн. ф-ция свободной ч-цы (z) — волна де Бройля — должна быть такой ф-цией координаты х, чтобы при изменении x на  волн. ф-ция  возвращалась к прежнему значению: (x+)=(x). Таким св-вом обладает ф-ция e^i2x/=e^lkx, где k=2/ — волн. число. Т. о., состояние ч-цы с определ. импульсом p=(h/2)k=ћk описывается волновой ф-цией:

=Ce^ikx=Ce^ipx/Ћ, (5)

где С — постоянное комплексное чис­ло. Квадрат модуля волн. ф-ции, ||², не зависит от х, т. е. вероятность нахождения ч-цы, описываемой такой , в любой точке пр-ва одинакова. Другими словами, ч-ца со строго опре­дел. импульсом совершенно нелокализована. Конечно, такая ч-ца — идеа­лизация (но идеализацией явл. и волна со строго определ. длиной вол­ны, а следовательно, и строгая опре­делённость импульса ч-цы). Поэтому точнее сказать иначе: чем более опре­делённым явл. импульс ч-цы, тем ме­нее определённо её положение (коор­дината). В этом заключается специфи­ческий для К. м. принцип неопреде­лённости. Чтобы получить количеств. выражение этого принципа — соот­ношение неопределённостей, рассмот­рим состояние, представляющее со­бой суперпозицию нек-рого (точнее, бесконечно большого) числа де-бройлевских волн с близкими k, заключён­ными в малом интервале k. Полу­чающаяся в результате суперпозиции волн. ф-ция (x), наз. волновым паке­том, имеет такой хар-р: вблизи нек-рого фиксиров. значения x₀ все амп­литуды сложатся, а вдали от х₀(|х—х₀|>>) будут гасить друг друга из-за большого разнобоя в фазах. Ока­зывается, что практически такая волн. ф-ция сосредоточена в области шири­ной Ах, обратно пропорц. интервалу k, т. е. x1/k, или xpЋ, где р=ћk:—неопределённость импульса ч-цы. Это соотношение и представляет собой соотношение неопределённо­стей Гейзенберга.

Математически любую ф-цию (x) с помощью преобразования Фурье мож­но представить как наложение про­стых периодич. волн, при этом соот­ношение неопределённостей между х и k получается математически строго. Точное соотношение имеет вид неравенства x^l/₂, или

рхћ/2, (6)

где под неопределённостями Ар и Ах понимаются среднеквадратичные от­клонения импульса и координаты от их ср. значений (т. е. дисперсии). Физ. интерпретация соотношения (6) за­ключается в том, что (в противополож­ность классич. механике) не суще­ствует такого состояния, в к-ром коор­дината и импульс ч-цы имеют одновре­менно точные значения. Масштаб их неопределённостей задаётся постоян­ной Планка Ћ. Если неопределённо­сти, связанные соотношением Гейзен­берга, можно считать в данной задаче малыми и пренебречь ими, то движение ч-цы будет описываться законами клас­сич. механики — как движение по определ. траектории.

Принцип неопределённости — фундам. принцип К. м., устанавливаю­щий физ. содержание и структуру её матем. аппарата. Кроме того, он игра­ет большую эвристич. роль, т. к. мн. результаты задач, рассматриваемых в К. м., могут быть получены и поняты на основе комбинации законов клас­сич. механики с соотношением неопре­делённостей. Важный пример — проб­лема устойчивости атома. Рассмотрим эту задачу для атома водорода. Пусть эл-н движется вокруг ядра (протона) по круговой орбите радиуса r со скоростью v. По закону Кулона, сила притяжения эл-на к ядру равна е²/r², где е — заряд эл-на, а центростремит. ускорение равно v²/r. По второму закону Ньютона, mv²/r=е²/r², где m — масса эл-на, т. е. радиус орбиты r=e²/mv² может быть сколь угодно малым, если v достаточно велика. Но в К. м. должно выполнять­ся соотношение неопределённостей. Если допустить неопределённость по­ложения эл-на в пределах радиуса его орбиты r, а неопределённость скоро­сти — в пределах v, т. е. импульса в пределах p=mv, то соотношение не-

256


определённостей примет вид: mvrћ. Учитывая связь между v и r, полу­чим vе²/ћ и rћ²/me². Следовательно, движение эл-на по орбите с r0=ћ²/me² 0,5•10^-8 см невозможно: эл-н не может упасть на ядро — атом устойчив. Величина r₀ и явл. радиу­сом атома водорода (боровским радиу­сом). Ему соответствует максималь­но возможная энергия связи атома ξ₀ (равная полной энергии эл-на в атоме, т. е. сумме кинетич. энергии mv²/2 и потенц. энергии — е²/r₀, что составляет: ξ₀=-е²/2r₀13,6 эВ), определяющая его мин. энергию — энергию осн. состояния.

Т. о., квантовомеханич. представ­ления впервые дали возможность тео­ретически оценить размеры атома, вы­разив его радиус через мировые по­стоянные ћ, т, е. «Малость» ат. раз­меров оказалась связанной с тем, что мала ћ.

Строгое решение задачи о движении эл-на в атоме водорода получается из квантовомеханич. ур-ния движе­ния — ур-ния Шредингера (см. ниже); решение ур-ния Шредингера даёт волн. ф-цию , к-рая описывает состояние эл-на, находящегося в области притя­жения ядра. Но и не зная явного вида , можно утверждать, что эта волн. ф-ция представляет собой та­кую суперпозицию волн де Бройля, к-рая соответствует локализации эл-на в области размером r₀ и разбросу по импульсам р ~ ћ/r₀.

Соотношение неопределённостей по­зволяет также понять устойчивость молекул и оценить их размеры и мин. энергию, объясняет св-ва гелия, к-рый при норм. давлении ни при каких темп-pax не превращается в тв. состояние, даёт качеств. представле­ния о структуре и размерах ядра и т. д.

Стационарное уравнение Шредин­гера. Волны де Бройля описывают со­стояние ч-цы только в случае свобод­ного движения. Если на ч-цу дейст­вует поле сил с потенц. энергией V, зависящей от координат ч-цы, то её волн. ф-ция  определяется дифф. ур-нием, к-рое получается путём след. обобщения гипотезы де Бройля. Для случая одномерного свободного дви­жения ч-цы (вдоль оси х) с пост. энер­гией ξ ур-ние, к-рому удовлетворяет волна де Бройля (5), может быть за­писано в виде:



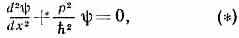
где р=2mξ — импульс свободно движущейся ч-цы массы m. Если ч-ца с энергией ξ движется в потенц. поле, не зависящем от времени, то квадрат её импульса (определяемый законом сохранения энергии) равен: р²=2m[ξ-V(x)]. Простейшим обобще­нием ур-ния (*) явл. поэтому ур-ние



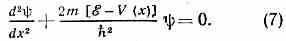
Оно наз. стационарным (не зависящим от времени) уравнением Шрёдингера и отно­сится к осн. ур-ниям К. м. Решение этого ур-ния зависит от вида сил, т. е. от вида потенциала, определяющего V(x). Рассмотрим два типичных слу­чая.

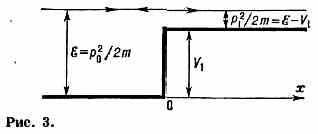
1) Потенциальная стенка:

V=0 при х<0, V=v₁>0 при х>0.

Если полная энергия ч-цы больше высоты стенки, т. е. ξ>V, и ч-ца движется слева направо (рис. 3), то решение ур-ния (7) в области x<0 имеет вид двух волн де Бройля — падающей и отражённой:



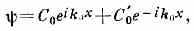
где ћ²k²₀/2m=p²₀/2m=ξ (волна с волн. числом k-=-k₀ соответствует движе­нию справа налево с тем же импульсом р₀),



а при х > 0 — проходящей волны де Бройля:

=C₁e^ik1x,

где ћ²k²₁/2m=p²₁l2m=ξ-V₁. Отноше­ния |C₁/C₀|² и |С'₀/С₀|² определяют ве­роятности прохождения ч-цы над стенкой и отражения от неё. Наличие отражения (т. н. надбарьерное отра­жение) — специфически квантовомеханическое (волновое) явление (ана­логичное частичному отражению све­товой волны от границы раздела двух прозрачных сред): «классич.» ч-ца свободно проходит над таким барье­ром (стенкой), и лишь импульс её уменьшается до значения р₁=((2m(e-V₁)).

Если ξ(рис. 4, a), то кине­тич. энергия ч-цы ξ-V в области x>0 отрицательна. В классич. механике это невозможно, и ч-ца не заходит в такую область пр-ва — она отража­ется от потенц. стенки. Волн. движе­ние имеет др. хар-р. Отрицат. значе­ние k²(p²/2m.=ћ²k²/2m<0) означает, что k — чисто мнимая величина, k=i, где  вещественно. Поэтому вол­на e^ikx превращается в е^-x, т. е. колебат. режим сменяется затухаю­щим (>0, иначе получился бы ли­шённый физ. смысла неогранич. рост волны с увеличением х). Под энергетич. схемой на рис. 4,а (и рис. 4, б) изображено качеств. по­ведение (x), точнее, её действит. части.

2) Две области, свободные от сил, разделены прямоуг. потенциальным барьером, и ч-ца движется к барьеру слева с энергией ξб). Согласно классич. механике, ч-ца отразится от барьера; согласно К. м.,

волн, ф-ция не равна нулю и внутри барьера, а справа, если барьер не слишком широк, будет опять иметь вид волны де Бройля с тем же импуль­сом (т. е. с той же частотой, но, ко­нечно, с меньшей амплитудой). Сле­довательно, ч-ца может пройти сквозь



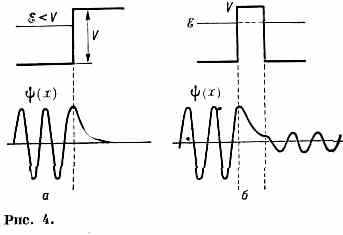
барьер. Коэфф. (или вероятность) про­никновения будет тем больше, чем меньше ширина и высота (чем меньше разность V-ξ) барьера. Этот типич­но квантовомеханич. эффект, наз. тун­нельным эффектом, имеет большое значение в практич. приложениях К. м. Он объясняет, напр., явле­ние альфа-распада (вылет из радио-акт. ядер -частиц). В термояд. ре­акциях, протекающих при темп-рах в десятки и сотни млн. градусов, осн. масса реагирующих ядер преодоле­вает электростатическое (кулоновское) отталкивание и сближается на расстояния порядка действия яд. сил в результате туннельных переходов. Туннельный эффект объясняет также автоэлектронную эмиссию, контакт­ные явления в металлах и ПП и мн. др. Уровни энергии. Рассмотрим пове­дение ч-цы в поле произвольной по­тенциальной ямы (рис. 5). Пусть V(x)0 в нек-рой огранич. области, причём V(x)<0 (что соответствует силам притяжения). Как классиче­ское, так и квант. движение существенно различны в зависимости от того, положительна или отрицательна пол­ная энергия ξ ч-цы.



При ξ>0 «клас­сич.» ч-ца проходит над ямой и уда­ляется от неё. В отличие от классич. случая, при квантовомеханич. дви­жении происходит частичное отраже­ние волны от ямы; при этом возмож­ные значения энергии ч-цы ничем не ограничены — её энергия имеет непрерывный спектр. При ξ<0 ч-ца оказывается «запертой» внутри ямы. В классич. механике эта огра­ниченность области движения абсо­лютна и возможна при любых значе­ниях ξ<0. В К. м. ситуация иная.

257


Волн. ф-ция должна затухать по обе стороны от ямы, т. е. иметь вид е^-\\. Однако решение, удовлетворяющее этому условию, существует не при всех значениях ξ, а только при опре­делённых дискретных значе­ниях. Число таких дискр. значений ξ_n может быть конечным или беско­нечным, но всегда счётно, т. е. может быть перенумеровано, и всегда име­ется низшее значение ξ₀, лежащее вы­ше дна потенц. ямы; номер решения n наз. квант. числом. Т. о., энергия ч-цы (или физ. системы) имеет дискретный спектр. Дискретность допустимых значений энергии систе­мы (или соответствующих частот =-ξ_n/ћ, где =2 — круговая ча­стота) — типично волн. явление. Его аналогии наблюдаются в классич. физике, когда волн. движение про­исходит в огранич. пр-ве. Так, частоты колебаний струны или частоты эл.-магн. волн в объёмном резонаторе дискретны и определяются размерами и св-вами границ области, в к-рой происходят колебания. Действитель­но, математически ур-ние Шредин­гера подобно соответствующим ур-ниям для струны или резонатора. Проиллюстрируем дискр. спектр

энергии на примере квант. осцилля­тора. На рис. 6 по оси абсцисс отло­жено расстояние ч-цы от положения



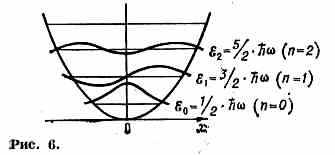
равновесия. Кривая (парабола) изоб­ражает собой потенц. энергию ч-цы. В этом случае ч-ца при всех энергиях «заперта» внутри ямы, поэтому спектр энергии дискретен. Горизонтальные прямые изображают уровни энергии ч-цы. Энергия низшего уровня ξ=Ћ/2 — наименьшее значение энер­гии, совместимое с соотношением неопределённостей: положение ч-цы на дне ямы (ξ=0) означало бы точное равновесие, при к-ром x=0 и р=0, что невозможно, согласно принципу неопределённости. Следующие, более высокие уровни энергии осцилля­тора расположены на равных расстоя­ниях с интервалом Ћ; ф-ла для энергии n-го уровня:



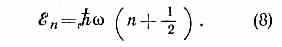
Над каждой горизонтальной прямой на рис. 6 приведена действит. часть волн. ф-ции данного состояния. Ха­рактерно, что число узлов волн. ф-ции равно квант. числу n уровня энергии. За пределами ямы волн. ф-ция быстро затухает.

В общем случае каждая квантовомеханич. система характеризуется сво­им энергетич. спектром. В зависимости от вида потенциала поля, определяю­щего потенц. энергию ч-цы (а следо­вательно, от хар-ра вз-ствия в систе­ме), энергетич. спектр может быть либо дискретным (как у осциллятора), либо непрерывным (как у свободной ч-цы), либо частично дискретным, ча­стично непрерывным (напр., уровни атома при энергиях возбуждения, меньших энергии ионизации, дискрет­ны, а при больших энергиях — не­прерывны).

Особенно важен случай, когда наи­низшее значение энергии, соответст­вующее осн. состоянию системы, лежит в области дискр. спектра и, следова­тельно, осн. состояние отделено от первого возбуждённого состояния энергетич. интервалом, наз. энер­гетической щелью. Такая ситуация характерна для атомов, мо­лекул, ядер и др. квант. систем. Благодаря энергетич. щели внутр. структура системы не проявляется до тех пор, пока обмен энергией при её вз-ствиях с др. системами не пре­высит определ. значения — ширины щели. Поэтому при огранич. обмене энергией сложная система (напр., яд­ро или атом) ведёт себя как бесструк­турная ч-ца (матер. точка). Это имеет первостепенное значение для понима­ния, в частности, особенностей тепло­вого движения ч-ц. Так, при энергиях теплового движения, меньших энер­гии возбуждения атома, ат. эл-ны не могут участвовать в обмене энергией и не дают вклада в теплоёмкость.