От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Квантовая оптика Квантовая радиофизика Квантовая теория многих частиц Квантовая теория поля Квантовая механика Квантование поля. N ч-цами вектор сос­тояния N N (n) может быть произвольным це­лым числом, т. е. в одном и том же состоянии n Паули принцип Ферми — Дирака статистике. Теория возмущений. Диаграммы Фейнмана. Виртуальные частицы. Комптона эффекта. Поляризация вакуума. Трудности теории возмущений. Эффективный заряд. Ренормализационная группа. Квантовая хромодинамика Другие подходы. Калибровочные симметрии и еди­ные теории поля. Квантовая химия Квантовая хромодинамика ... Полное содержание

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КВАНТОВАЯ ОПТИКА, раздел статистической оптики, изучающий микроструктуру световых полей и оптич. явления, в к-рых видна квант. природа света. Представление о квант. структуре излучения введено нем. физиком М. Планком в 1900.

262


Статистич. структуру интерференц. поля впервые наблюдал С. И. Вави­лов (1934), им же предложен термин «микроструктура света».

Световое поле — сложный физ. объект, состояние к-рого определя­ется бесконечным числом параметров. Это относится и к монохроматическо­му излучению, к-рое при классич. описании характеризуется полностью амплитудой, частотой, фазой и поля­ризацией. Задача полного определе­ния состояния светового поля не мо­жет быть решена из-за непреодоли­мых технич. трудностей, связанных с бесконечным числом измерений пара­метров поля. Дополнит. сложности в решение этой задачи вносит сущест­венно квант. хар-р измерений, т. к. они связаны с регистрацией фотонов фотодетекторами.

Успехи лазерной физики и совер­шенствование техники регистрации слабых световых потоков определили развитие и задачи К. о. Долазерные источники света по своим статистич. св-вам однотипны генераторам шума, имеющего гауссовское распределение. Состояние их полей практически полно определяется формой спектра излу­чения и его интенсивностью. С появ­лением квант. генераторов и квант. усилителей К. о. получила в своё распоряжение широкий ассортимент источников с весьма разнообразными, в т. ч. не гауссовскими, статистич. хар-ками.

Простейшая хар-ка поля — его ср. интенсивность. Более полная хар-ка— ф-ция пространственно-временного распределения интенсивности поля, определяемая из экспериментов по регистрации во времени фотонов од­ним детектором. Ещё более полную информацию о состоянии поля дают исследования квант. флуктуации его разл. величин, к-рые удаётся частично определить из экспериментов по со­вместной регистрации фотонов поля неск. приёмниками, либо при иссле­довании многофотонных процессов в в-ве.

Центр. понятиями в К. о., опреде­ляющими состояние поля и картину его флуктуации, явл. т. н. корреля­ционные ф-ции или полевые корреля­торы. Они определяются как квантовомеханич. средние от операторов поля (см. Квантовая теория поля). Степень сложности корреляторов определяет ранг, причём, чем он выше, тем более тонкие статистич. св-ва поля им харак­теризуются. В частности, эти ф-ции определяют картину совместной ре­гистрации фотонов во времени про­извольным числом детекторов. Кор­реляционные ф-ции играют важную роль в нелинейной оптике. Чем выше степень нелинейности оптич. процес­са, тем более высокого ранга корреля­торы необходимы для его описания. Особое значение в К. о. имеет поня­тие квантовой когерентности. Раз­личают частичную и полную когерент­ность поля. Полностью когерентная

волна по своему действию на системы максимально подобна классич. монохроматич. волне. Это означает, что квант. флуктуации поля когерентной волны минимальны. Излучение ла­зеров с узкой спектральной полосой близко по своим хар-кам к полностью когерентному.

Исследование корреляц. ф-ций выс­ших порядков позволяет изучать физ. процессы в излучающих системах (напр., в лазерах). Методы К. о. дают возможность определять детали межмол. вз-ствнй по изменению ста­тистики фотоотсчётов при рассеянии света в среде.

• Глаубер Р.. Оптическая когерентность и статистика фотонов, в кн.: Квантовая оп­тика и квантовая радиофизика, М., 1966; Клаудер Д ж., С у д а р ш а н Э., Ос­новы квантовой оптики, пер. с англ., М., 1970; Спектроскопия оптического смещения и корреляции фотонов, под ред. Г. Камминса и Э. Пайка, пер. с англ., М., 1978; Вави­лов С. И., Микроструктура света, М., 1950.

С. Г. Пржибельский.

КВАНТОВАЯ РАДИОФИЗИКА, см. Квантовая электроника.

КВАНТОВАЯ СТАТИСТИКА, раздел статистической физики, исследующий системы мн. ч-ц, подчиняющихся законам квант. механики.

КВАНТОВАЯ ТЕОРИЯ МНОГИХ ЧАСТИЦ, раздел квант. теории, посвя­щённый изучению систем, состоящих из трёх и большего числа ч-ц. В квант. механике система из N ч-ц описыва­ется при помощи волн. ф-ции, завися­щей как от координат всех ч-ц, так и от всех др. величин, необходимых для задания состояния каждой ч-цы («внутр. переменных»). Если рассмат­ривается такая система, к-рая явл. частью большой подсистемы, то опи­сание производится с помощью мат­рицы плотности.

Точное решение задачи мн. тел в квантовой, как и в классической, тео­рии встречает чрезвычайно большие затруднения. Однако можно указать нек-рые общие св-ва симметрии, вы­текающие из принципа Паули. Волн. ф-ция для систем, состоящих из нек-рого числа одинаковых (тождественных) ч-ц с полуцелым спином (фермионов), явл. антисимметричной, т. е. её знак изменяется при перестановках пере­менных (включая внутренние) двух ч-ц. Для систем ч-ц с целым спином — бозонов такая перестановка не меняет знака волн. ф-ции, т. е. волн. ф-ция симметрична. Различие в св-вах сим­метрии фермионов и бозонов опреде­ляет качеств. отличие в поведении систем, состоящих из ч-ц этих двух типов, в частности их распределение по состояниям (уровням энергии), да­ваемое Бозе — Эйнштейна статисти­кой (для бозонов) или Ферми — Ди­рака статистикой (для фермионов). В бозе-системах в данном квант. со­стоянии может находиться произволь­ное число ч-ц, и поэтому при абс. темп-ре Т  0 (при отсутствии источ­ников возбуждения) все бозоны будут скапливаться на низшем возможном уровне энергии. В ферми-системах

каждое квант. состояние может за­нимать лишь одна ч-ца и поэтому они в сходных условиях заполняют все уровни от низшего до нек-рого гра­ничного (уровня Ферми ξ_F).

Приближённые методы, привле­каемые для решения проблемы мн. тел, приобрели значительно большую эффективность после того, как нача­лось широкое использование представ­лений квантовой теории поля (КТП). Так, при рассмотрении тв. тела можно принять его состояние при нулевой абс. темп-ре за «вакуумное», посколь­ку энергия такого состояния мини­мальна. Возбуждение тв. тела, в ча­стности при его нагревании, можно рассматривать как рождение элем. возбуждений — квантов, каждый из к-рых несёт определённую энергию, импульс и спин. Такие элем. возбуж­дения наз. квазичастицами (в отличие от «истинных» ч-ц — структурных элементов кристалла, напр. атомов, число к-рых неизменно). Привлечение методов КТП, позволяющих предста­вить эволюцию системы как рождение, вз-ствие и взаимные превращения разл. квазичастиц, оказалось весьма плодотворным для физики тв. тела. Примером может служить создание теории сверхпроводимости.

Несколько иной подход удобно ис­пользовать при описании многоэлект­ронных атомов. Сначала принима­ется, что эл-ны независимы, т. е. что каждый из них испытывает лишь влия­ние нек-рого т. н. самосогласованного поля, в к-ром эффективно учитываются как кулоновское поле ядра, так и усреднённое поле вз-ствия между эл-нами. При таком подходе задача о движении каждого из эл-нов (одноэлектронная задача) решается относитель­но просто. Получаются, как и обычно в квант. механике, наборы возможных состояний с разл. значениями квант. чисел, определяющих энергии, мо­менты кол-ва движения и др. физ. величины. В соответствии с принци­пом Паули заполнение эл-нами уров­ней энергии происходит так, что вначале исчерпываются все возмож­ные наборы квант. чисел в состоянии с наинизшей возможной энергией, затем заполняются более высокие уровни и т. д., пока не будут разме­щены все эл-ны. При этом в осн. состоянии системы окажутся запол­ненными все уровни энергии, начиная от наинизшего вплоть до нек-рого предельного значения ξ_F; такое со­стояние можно считать «вакуумным». Все более высокие уровни остаются вакантными. Дополнит. влияние неуч­тённых при этом вз-ствий можно рас­сматривать квантовополевыми ме­тодами. Эти вз-ствия могут приводить к реальному или виртуальному пере­бросу эл-нов с заполненных уровней на свободные (вакантные), что можно описывать как рождение пары: «над

263


вакуумом» возникает ч-ца, а на осво­бодившемся уровне появляется «дыр­ка», к-рая играет роль античастицы. Рождение таких пар и их аннигиля­ция могут быть изображены Фейнмана диаграммами. Если вероятность одноврем. образования мн. пар мала, можно упростить задачу, ограничив­шись учётом рождения и аннигиляции лишь небольшого их числа.

Квантовополевые методы, перене­сённые в физику многочастичных си­стем, оказались здесь даже более эффективными, чем в породившей эти методы физике элем. ч-ц. Более того, КТП получила в новой области такое дальнейшее развитие, к-рое может оказаться полезным и для теории элем. ч-ц. В. И. Григорьев.

КВАНТОВАЯ ТЕОРИЯ ПОЛЯ (КТП), релятивистская квант. теория физ. систем с бесконечным числом степе­ней свободы. Пример такой системы — эл.-магн. поле, для полного описания к-рого в любой момент времени тре­буется задание напряжённостей электрич. и магн. полей в каждой точке пр-ва, т. е. задание бесконечного числа величин. В отличие от этого, положение ч-цы в каждый момент времени определяется заданием трёх её координат.

Квантовая механика значительно сблизила эти два объекта — ч-цы и поля. Согласно квант. механике, эл.-магн. излучение порождается и погло­щается дискр. порциями — кван­тами, или фотонами, к-рые, как и ч-цы, имеют определённую энергию ξ =h и импульс р=h/, где  и  — частота и длина волны излуче­ния. С другой стороны, с каждой ч-цей сопоставляется волновая функция (r, t) и полное описание ч-цы требует задания величины  в любой точке пр-ва в каждый момент времени, при этом ч-це приписываются волн. св-ва: частота =ξ/h и дл. волны =p/h, где ξ и р — энергия и импульс ч-цы.

Рождаться и исчезать могут не только фотоны. Одно из самых об­щих св-в микромира — универсальная взаимная превращаемость ч-ц. Так, фо­тон может породить пару электрон-позитрон; при столкновении протонов и нейтронов могут рождаться -мезоны; -мезон распадается на мюон и нейтрино и т. д. Для описания тако­го рода процессов потребовался пере­ход к квантовому волн. полю (r, t), т. е. построение квант. теории систем с бесконечным числом степеней свободы, получившей назв. КТП.

Поясним этот переход с помощью механич. аналогии. Представим, что всё пр-во заполнено связанными между собой осцилляторами. Такая система имеет бесконечно большое число сте­пеней свободы, и её можно рассматри­вать как поле. Связи между осциллято­рами приводят к тому, что в системе могут возникать коллективные колебания, к-рые характеризуются своими собств. частотами, а по системе могут распространяться волны соответствую­щих колебаний.

При переходе к квантовой меха­нике коллективные колебания кван­туются, а возникающие при этом кван­ты могут рассматриваться как части­цы, обладающие, как и волны, энер­гией и импульсом (следовательно, и нек-рой массой). Очевидно, что эти ч-цы — кванты возбуждения системы нельзя ассоциировать с отд. исходны­ми осцилляторами, находящимися в фиксиров. точках пр-ва. Они представ­ляют собой результат процесса, за­хватывающего всю систему в целом, и описывают нек-рые возбуждения поля. Т. о., изучение поля можно свести к рассмотрению квантованных волн (или ч-ц) возбуждений, их рождения и поглощения. Строго говоря, свобод­ное квант. поле может быть представ­лено как подобная бесконечная сово­купность осцилляторов, заполняющих не обычное, координатное, а 3-мерное импульсное пр-во. Описанная механич. система, однако, реализуется, напр., в теории кристаллов, где число степе­ней свободы конечно и можно ограни­читься нерелятив. приближением.

КТП с необходимостью должна быть релятивистской теорией. Дей­ствительно, теория относительности устанавливает связь между энергией ξ, импульсом р и массой m ч-цы:



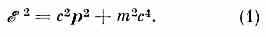
Из (1) видно, что мин. энергия (энер­гия покоя ч-цы), необходимая для образования ч-цы данной массы, рав­на mc². Если система состоит из мед­ленно движущихся ч-ц, то их энер­гия может оказаться недостаточной для образования новых ч-ц ненулевой массы. В такой нерелятив. системе число ч-ц неизменно. Ч-цы же с ну­левой массой покоя (фотон, возможно нейтрино) всегда релятивистские, т. е. всегда движутся со скоростью света.

Квантование поля. Метод квантова­ния систем с перем. числом ч-ц (вто­ричное квантование) был предложен в 1927 англ. физиком П. Дираком и получил дальнейшее развитие в ра­ботах В. А. Фока (1932). Осн. его черта — введение операторов, описы­вающих рождение и уничтожение ч-ц. Поясним их действие на примере оди­наковых (тождественных) ч-ц, на­ходящихся в одном и том же состоянии (напр., все фотоны считаются имею­щими одинаковые частоту, направле­ние распространения и поляризацию).

В квант. теории состояние системы ч-ц описывается волн. ф-цией или вектором состояния. Введём для описа­ния состояния с N ч-цами вектор сос­тояния _N. Квадрат его модуля |_N|², определяющий вероятность данного состояния, равен единице, т. к. N достоверно известно. Введём опера­торы уничтожения и рождения ч-цы: а^- и а⁺. По определению, а~ переводит состояние с N ч-цами в состоя­ние с N-1 ч-цами:



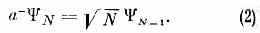
Аналогично оператор рождения ч-цы а* переводит состояние с N ч-цами в состояние с N+1 ч-цами:



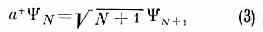
(множители N и (N+1) вводят для выполнения условия нормировки |_N|²=1). В частности, при N=0 а⁺₀=₁, где ₀ — вектор, характе­ризующий вакуумное состояние, т. е. состояние с нулевым числом ч-ц и мин. энергией. Т. о., одночастичное состояние получается в результате рождения из вакуума одной ч-цы, Поскольку невозможно уничтожить ч-цу в состоянии, в к-ром ч-ц нет, то a^-₀=0. Это равенство можно счи­тать определением вакуума. Особое значение вакуумного вектора состоя­ния состоит в том, что из него дей­ствием оператора а⁺ можно получить вектор любого состояния:



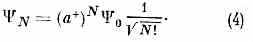
Порядок действия а^- и а⁺ не безразли­чен. Так,



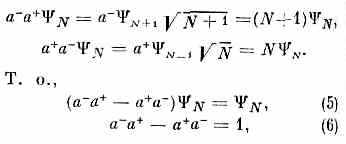
т. е. операторы а^-, а⁺ явл. непереставимыми (некоммутирующими). Соотношения типа (6), устанавливающие связь между действием двух операто­ров, взятых в разл. порядке, наз. коммутационными или перестановоч­ными соотношениями. Если учесть, что ч-цы могут находиться в разл. состояниях, то следует дополнитель­но указывать, к какому состоянию относятся операторы рождения и унич­тожения (т. е. квант. числа состоя­ния — энергию, спин и др.). Для про­стоты обозначим всю совокупность квант. чисел, определяющих состоя­ние, индексом га; тогда а⁺_т(а^-_т) обо­значает оператор рождения (уничтоже­ния) ч-цы в состоянии с набором квант. чисел n. Числа ч-ц, находя­щихся в состояниях, соответствую­щих разл. n, наз. числами заполнения этих состояний, а задание вектора со­стояния в форме, фиксирующей числа заполнения всех возможных состоя­ний системы,— представлени­ем чисел заполнения.

Если nm, то a^-_na⁺_m₀=0, по­скольку невозможно уничтожение ч-ц в таких состояниях, к-рых нет в систе­ме. С учётом этого перестановочные соотношения имеют вид:



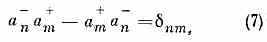
264


где _nm — символ Кронекера: _nm=1 при n=m и _nm=0 при nm.

Из а⁺_n и a^-_n можно построить игра­ющий важную роль оператор числа ч-ц: N(n) = a⁺_na^-_n [это ясно из приведенного выше равенства a⁺_na^-_n_N=N(n)_N]. Через собств. значения N(n) этого оператора выражаются все «кор-1пускулярные» величины, характери­зующие систему,—импульс (Р), энер­гия (В), электрич. заряд (Q) и т. д.:

P=_ppN(p), ξ=_pξ(p)N(p), Q=_peN(p)=eN. Здесь N(р) — чис­ло ч-ц системы, имеющих импульс р, ξ(р) — энергия ч-цы с импульсом р, е — заряд ч-цы (одинаковый для всех ч-ц).

Вакуумное состояние. В квант. ме­ханике доказывается, что если два к.-л. оператора не коммутируют, то соответствующие им физ. величины не могут одновременно иметь точно опре­делённые значения. Так, не сущест­вует состояния эл.-магн. поля, в к-ром были бы одновременно точно определенными напряжённости поля и число фотонов, поскольку относящиеся к этим величинам операторы непереставимы. Поэтому из определения ва­куума как состояния с нулевым чис­лом ч-ц вытекает неопределённость напряжённостей поля в вакуумном сос­тоянии, в частности невозможность этих напряжённостей иметь точно ну­левые значения. Именно в невозмож­ности одноврем. равенства нулю и числа фотонов, и напряжённостей электрич. и магн. полей лежит физ. причина необходимости рассматривать вакуумное состояние не как простое от­сутствие поля, а как одно из возмож­ных состояний поля, обладающее оп­ределёнными св-вами, к-рые могут проявляться на опыте (см. Радиаци­онные поправки).

Связь спина со статистикой. Пра­вила перестановок (6) справедливы для ч-ц, имеющих целый спин. Для них N (n) может быть произвольным це­лым числом, т. е. в одном и том же состоянии n может находиться любое число ч-ц. Такие ч-цы (бозоны) под­чиняются Возе — Эйнштейна ста­тистике. Для ч-ц с полуцелым спи­ном (фермионов) знак минус в (6) заменяется на знак плюс:



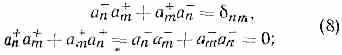
эти соотношения наз. антикоммутационными. Они связаны с тем, что для фермионов справедлив Паули принцип, согласно к-рому в системе одинаковых ч-ц (напр., эл-нов) в любом состоянии может находиться не более одной ч-цы. Действительно, согласно (8), вектор состояния, со­держащий, напр., две ч-цы, при n=m равен самому себе с обратным знаком:

a⁺_na⁺_n₀=-a⁺_na⁺_n₀, что возможно только для величины, тождественно равной нулю. Такие

ч-цы подчиняются Ферми — Дирака статистике.

Взаимодействие в КТП. До сих пор рассматривались свободные невзаимо­действующие ч-цы, число к-рых ос­тавалось неизменным; как нетрудно показать с помощью соотношений (6), оператор числа ч-ц N(n)=a⁺_na^-_n ком­мутирует с оператором энергии ξ=ξ(p)N(p), поэтому число ч-ц должно быть постоянным, т. е. про­цессы появления дополнит. ч-ц, их исчезновение и взаимопревращения отсутствовали. Учёт этих процессов требует включения вз-ствия ч-ц.

В классич. электродинамике вз-ствие между заряж. ч-цами осуще­ствляется через ноле: заряд создаёт поле, к-рое действует на др. заряды. В квант. теории вз-ствие эл.-магн. поля и заряж. ч-цы выглядит как испускание и поглощение ч-цей фо­тонов, а вз-ствие между заряж. ч-цами явл. результатом их обмена фото­нами: каждый из эл-нов испускает фотоны (кванты переносящего вз-ствие эл.-магн. поля), к-рые затем погло­щаются др. эл-намн. Подобная кар­тина вз-ствия возникает благодаря особому св-ву электродинамики — т. н. калибровочной симметрии. Ана­логичный механизм вз-ствия находит всё большее подтверждение и для др. физ. полей. Однако свободная ч-ца ни испустить, ни поглотить кван­та не может. Напр., в системе, где ч-ца покоится, излучение кванта тре­бует затраты энергии и уменьшения массы ч-цы (в силу эквивалентности энергии и массы), что невозможно. Чтобы разрешить этот парадокс, нужно учесть, что рассматриваемые ч-цы— квант. объекты, для к-рых существенно неопределённостей соот­ношение ξtћ, допускающее из­менение энергии ч-цы на величину ξ и, следовательно, излучение или по­глощение квантов ноля при условии, что эти кванты существуют в течение промежутка времени tћ/ξ. (На основе подобных рассуждений и факта короткодействия яд. сил япон. физик X. Юкава предсказал существование ч-цы — переносчика яд. вз-ствия с массой прибл. в 200—300 электрон­ных масс, к-рая впоследствии была обнаружена экспериментально и на­звана -мезоном.)

Теория возмущений. Диаграммы Фейнмана. Виртуальные частицы. Для расчёта процессов в КТП часто используется метод теории возмуще­ний, к-рый заключается в поэтапном учёте всё большего числа актов вз-ствия свободных ч-ц. Каждому эта­пу учёта вз-ствия можно дать нагляд­ное графич. изображение. Такого рода графики, или диаграммы, были впер­вые введены амер. физиком Р. Фейнманом и носят его имя.

Введём для изображения каждой свободной ч-цы нек-рую линию, пред­ставляющую собой лишь графич. сим­вол распространения ч-цы: фотону — волнистую, эл-ну — сплошную. Иног­да на линиях ставят стрелки, условно обозначающие «направление» распро­странения ч-цы. В первом, втором и т. д. приближениях учитываются од­нократные, двукратные и т. д. акты вз-ствия между разл. ч-цами (поля­ми). Разная последовательность та­ких элем. актов соответствует разл.



физ. процессам, а число актов вз-ствия наз. порядком диаграммы. (На всех диаграммах Фейнмана ось времени будет считаться направлен­ной вправо.) На рис. 1 изображена диаграмма 2-го порядка, соответст­вующая рассеянию фотона на эл-не: в нач. состоянии присутствуют эл-н и фотон, в точке 1 они встречаются и происходит поглощение фотона эл-ном, в точке 2 появляется (испускается эл-ном) новый, конечный фо­тон.



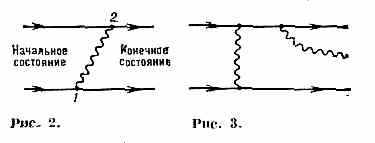
Это — одна из простейших ди­аграмм Комптона эффекта. Диаг­рамма 2-го порядка на рис. 2 отра­жает процесс обмена фотоном между двумя эл-нами: один эл-н в точке 1 испускает фотон, к-рый затем в точ­ке 2 поглощается вторым эл-ном. Эта диаграмма изображает элем. акт эл.-магн. вз-ствия двух эл-нов. Более сложные диаграммы, соответствую­щие такому вз-ствию, должны учи­тывать возможность обмена неск. фо­тонами, а также испускание и погло­щение фотона одним и тем же эл-ном (т. н. радиационные поправки). На рис. 3 изображена диаграмма 3-го порядка, описывающая вз-ствие двух эл-нов с излучением фотона (тормоз­ное излучение).

В приведённых примерах проявля­ется нек-рое общее св-во диаграмм: все они составляются из простейших



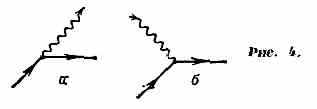
элементов — вершинных частей, или вершин, представляющих собой либо испускание (рис. 4, а) и поглощение (рис. 4, б) фотона эл-ном, либо рож­дение фотоном электрон-позитронной пары (рис. 5, а) или её аннигиляцию

265


в фотон (рис. 5, б) (античастица изоб­ражается такой же линией, что и ч-ца, но направленной «вспять по времени», ибо, согласно теореме СРТ, погло­щение ч-цы эквивалентно испуска­нию античастицы). Каждый из этих



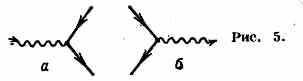
процессов запрещён законами сохра­нения энергии-импульса. Однако если такая вершина входит составной ча­стью в более сложную диаграмму (как в рассмотренных примерах), то квант. неопределённость снимает этот запрет.

Ч-цы, к-рые рождаются и затем по­глощаются на промежуточных этапах процесса, наз. виртуальными, в отличие от реальных ч-ц, существу­ющих достаточно длит. время. На рис. 1 это — виртуальный эл-н, воз­никающий в точке 7 и исчезающий в точке 2, на рис. 2 — виртуальный фотон и т. д. Т. о., вз-ствие осуществ­ляется путём испускания и поглоще­ния виртуальных ч-ц. Можно не­сколько условно принять, что ч-ца виртуальна, если квант. неопределён­ность её энергии ξпорядка ср. значения её энергии. Более распро­странён др. подход к описанию вир­туальных ч-ц, основанных на соот­ношении (1). Для виртуальных ч-ц это соотношение несправедливо; ква­драт их «массы» ξ²/с⁴-p²/с² не равен m², а принимает всевозможные значе­ния, причём разброс последних по отношению к т² тем больше, чем более «виртуальна» ч-ца. Такой подход поз­воляет считать, что в каждом элем. процессе вз-ствия сохраняются и энер­гия, и импульс, квантовые же неопре­делённости переносятся на массы вир­туальных ч-ц.

Диаграммы Фейнмана позволяют при помощи определённых матем. пра­вил находить вероятности соответ­ствующих процессов. Не останавли­ваясь детально на этих правилах, отметим, что вклад каждой из вершин в амплитуду процесса (квадрат абс. величины к-рой определяет его ве­роятность, или эфф. сечение) пропорц. константе связи тех ч-ц (или полей), линии к-рых встречаются в вершине. Во всех приведённых диаг­раммах такой константой явл. электрич. заряд е. Чем больше вершин содержит диаграмма процесса, тем в более высокой степени входит за­ряд в соответствующее выражение для амплитуды. Так, амплитуда, соответ­ствующая диаграммам на рис. 1 и 2 с двумя вершинами, пропорц. е², а диаграмма на рис. 3, содержащая три вершины, пропорц. е³. Если диаг­раммы содержат замкнутые циклы (см. ниже рис. 6, 7, б и 8, б — д), то законы сохранения четырёхмерных импуль­сов (4-импульсов) р(ξ/с, р), где р²= ξ²/c²-р², в каждой вершине не позволяют выразить 4-импульсы всех виртуальных ч-ц через 4-импульсы нач. и конечных ч-ц; импульс одной из них оказывается неопределённым, и необходимо производить интегри­рование по всем его значениям.

Расходимости. В нек-рых случаях это интегрирование приводит к бес­конечно большим выражениям (расходимостям), причина к-рых в том, что в теории используется предполо­жение о точечности свободных ч-ц. На графике вз-ствия двух эл-нов (рис. 2) фотон рождается одним и по­глощается другим эл-ном. Однако возможен и процесс, в к-ром вирту­альный фотон испускается и поглоща­ется одним и тем же эл-ном (рис. 6).



Т. к. обмен квантами обусловливает вз-ствие, то такой график явл. одной из простейших диаграмм вз-ствия эл-на с самим собой, или с собств. полем. Этот процесс можно также назвать вз-ствием эл-на с фотонным вакуумом, поскольку реальных фотонов здесь нет. Т. о., собств. эл.-магн. поле эл-на создаётся испусканием и поглощением этим же эл-ном виртуальных фотонов. Наличие такого самодействия при­водит к увеличению массы эл-на и в классич. электродинамике: поле, по­рождаемое эл-ном, обладает нек-рой энергией, а следовательно, и массой, и при ускорении эл-на нужно прео­долевать также инерцию его эл.-магн. (в простейшем случае — кулоновского) поля. Т. о., и в классич., и в квант. теории поля к «неполевой», или «затравочной», массе m₀ ч-цы необходимо добавить «полевую» часть. Вычисление полевой массы, однако, приводит к бесконечной величине (диа­грамма рис. 6 расходится).

Поляризация вакуума. Аналогичная трудность встречается и при вычисле­нии заряда эл-на, к-рый обычно опре­деляется через вз-ствие эл-на с внеш.



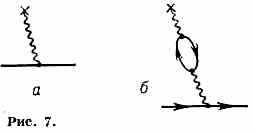
электростатич. полем. В низшем при­ближении это вз-ствие описывается диаграммой рис. 7, а (крестиком на диаграмме обозначен источник элек­тростатич. поля). В след. приближе­нии (рис. 7, б) необходимо учесть, что виртуальный фотон может поро­дить из вакуума виртуальную пару электрон-позитрон, к-рая взаимодей­ствует с полем эл-на. Реальный эл-н притягивает виртуальные позитроны и отталкивает виртуальные эл-ны. Это приводит к явлениям, напоминающим поляризацию среды, в к-рую вносится заряж. ч-ца (отсюда назв. явления). Эл-н оказывается окружён­ным слоем позитронов из виртуаль­ных пар, так что его эфф. заряд из­меняется: возникает экранировка за­ряда, т. е. первоначальный, «затра­вочный», заряд е₀ приобретает отрицат. добавку (эфф. заряд уменьшается). Вычисление же этой добавки (диаг­раммы рис. 7, б) даёт бесконечную ве­личину.

Перенормировка. Анализ встретив­шихся трудностей привёл к идее пе­ренормировок. Оказалось, что в квант. электродинамике и нек-рых др. тео­риях в выражениях для физ. величин бесконечно большие значения всегда появляются лишь в виде добавок к затравочной массе или к затравочному заряду, так что невозможно экспе­риментально отделить эти части друг от друга (такие теории наз. ренормируемыми или перенормируемыми). Перенормировка заключается в ис­пользовании для суммы этих частей эксперим. значений массы и заряда. Это позволяет перестроить разложение (по методу теории возмущений) по е₀ разложением по физ. заряду е, уже не содержащему бесконечных величин (подробнее см. Перенормировка). Од­нако не всегда перенормировка ко­нечного числа величин устраняет рас­ходимости. В нек-рых случаях рассмо­трение диаграмм всё более высокого порядка приводит к появлению расходимостей новых типов, тогда гово­рят, что теория неперенормируема. (Таковы, напр., первые варианты тео­рии слабого вз-ствия.)

Перенормировка заряда и массы даёт возможность выделить конечные наблюдаемые части из бесконечных значений для величин, характеризу­ющих физ. ч-цы. Особое значение это имеет для квант. электродинамики, где каждая вершина соответствую­щей диаграммы Фейнмана вносит в выражение для амплитуды процесса множитель е (точнее, безразмерную величину e/ћc). Т. к. внутр. линии имеют два конца (соединяют две вер­шины), добавление каждой внутр. линии изменяет амплитуду прибл. в =е²/ћc¹/₁₃₇ раз. Если записать ам­плитуду в виде бесконечной суммы членов с возрастающими степенями а, то такому ряду будут соответствовать диаграммы со всё большим числом внутр. линий. Каждый член ряда дол­жен быть примерно на два порядка меньше предыдущего, так что высшие диаграммы должны вносить ничтожно малый вклад и могут быть отброшены. Это позволяет понять, почему именно в квант. электродинамике достигнуто рекордное согласие теории и экспе­римента. Напр., вычисления магн. момента эл-на согласуются с его эксперим. значением с точностью до одной миллиардной доли %.

Трудности теории возмущений. Бо­лее внимат. рассмотрение показывает,

266


что число высших диаграмм факториально растёт (пропорц. n! = 1•2•3• . . . ... •n, где n — число виртуальных фо­тонных линий). Для достаточно вы­сокого порядка (т. е. для достаточно большого числа внутр. линий) число диаграмм настолько велико, что пере­крывает малый множитель ⁿ, и по­правка с ростом порядка диаграмм увеличивается, а сумма всего ряда оказывается бесконечной. Такие ряды

(напр., сумма



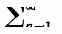
n!ⁿ=+2²+6³+. . .) наз. асимптотическими. В отличие от конечных (сходящихся) рядов, к-рые позволяют, взяв до­статочно большое число членов, про­водить вычисления со сколь угодно большой точностью, асимптотич. ряды могут обеспечить лишь нек-рую ко­нечную точность, зависящую от ве­личины а. Для квант. электродина­мики этот недостаток теории возмуще­ний не создаёт особых трудностей, поскольку предельная точность вы­числения величин, определяемых та­ким рядом, столь высока (~10^-57%), что практически может считаться аб­солютной. Иное положение в теории сильного вз-ствия, где эфф. константа связи g, напр. двух нуклонов (т. е. величина, играющая роль заряда в сильном вз-ствии), велика: g²/ћc14 —15. Поэтому те аргументы, к-рые в электродинамике оправдывают от­брасывание высших диаграмм (т. е. ис­пользование низших приближений те­ории возмущений), здесь теряют силу.

Эффективный заряд. Ренормализационная группа. Процедура перенор­мировки придала квант. электроди­намике черты логич. замкнутости. Однако даже в этой теории проблема самосогласованности не может считаться решённой. Одно из усложнений простейших диаграмм Фейнмана (рис. 1,2) состоит в том, что каждая



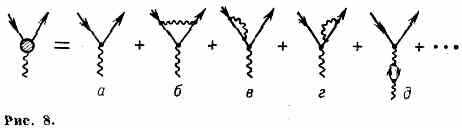
из входящих в них вершин типа изо­бражённых на рис. 4 и 5 может быть дополнена диаграммами более высоких порядков (рис. 8). В сумме они обра­зуют т. н. вершинную часть (своего рода формфактор эл-на) — нек-рую ф-цию Е(m*) (на рис. 8 изображённую в виде заштрихованного кружка), зави­сящую от эфф. массы m* (m*²с²=|Q²|, где Q²— квадрат передачи четырёх­мерного импульса эл-ном фотону) вир­туального фотона и представляющую собой (после проведения перенорми­ровки) ряд по степеням заряда е. Ф-ция Е(m*), т. о., играет роль эф­фективного заряда, зависящего от рас­стояния, на к-ром происходит вз-ствие. (Согласно соотношению не­определённостей, большая величина квадрата переданного 4-пмпульса

соответствует малым расстояниям, и наоборот.)

Условие самосогласованности пе­ренормировки приводит к дифф. ур-нию для ф-цин Е (m*):



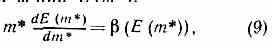
где (Е) имеет вид ряда по Е, опре­деляемого диаграммами рис. 8. В ча­стности, для диаграммы 8,a =0, а для суммы диаграмм 8, б — д (в пре­деле m*>>m_е, где m_е — масса эл-на) (E)=(1/Зћc)Е³. Простой подста­новкой можно проверить, что реше­нием ур-ния (9) с таким (Е) будет



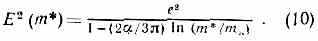
Гл. особенность выражения (10) сос­тоит в том, что с ростом m* (с умень­шением расстояния) эфф. заряд рас­тёт. Это и есть рассмотренный выше эффект экранировки заряда вакуумом. При массе m*=m_ее^з/2 знамена­тель выражения (10) обращается в нуль, а сам заряд становится бес­конечно большим. В результате появ­ляется лишённое физ. смысла огра­ничение на величину передачи 4-импульса, т. е. квант. электродинамика оказывается несамосогласованной, хо­тя это проявляется при фантастически высоких энергиях (~10²⁸⁰ эВ!), пре­восходящих энергию Вселенной. Од­нако как только заряд становится большим, неправомерно ограничивать­ся первыми слагаемыми в разложе­нии (Е), а необходимо рассматри­вать весь ряд. Из-за асимптотич. хар-ра ряда теории возмущений по Е сумма его бесконечно велика при любом значении Е. В математике раз­работаны методы обращения с подоб­ными рядами и сопоставления с ними конечных величин, но для этого не­обходимы какие-то дополнит. сведения о св-вах ф-ций (E). Т. о., воп­рос самосогласованности квант. элект­родинамики остаётся открытым.

Из изложенного выше следует, что формальное использование метода возмущений порождает определённые трудности. Даже введение в теорию новой фундам. постоянной (имеющей смысл фундаментальной длины) либо путём «размазывания» вз-ствия по нек-рой области пространства-вре­мени (см. Нелокальная теория поля), либо путём перехода к квантованному пространству-времени (см. Кванто­вание пространства-времени) не устра­няет этого дефекта теории возмуще­ний, если продолжать пользоваться её традиц. формой. Хотя все диаграммы становятся конечными, ряд для ф-ции  остаётся бесконечным асимптотич.

рядом и по-прежнему неизвестно, как определить его сумму, т. е. вы­яснить хар-р поведения зфф. заряда на малых расстояниях. Подобная же проблема самосогласованности оста­ётся и в объединённой теории слабого и эл.-магн. вз-ствий (см. Слабое взаи­модействие).

Квантовая хромодинамика (КХД) и асимптотическая свобода. Иная си­туация в квантовой хромодинамике — теории, претендующей на описание



сильного вз-ствия кварков и глюонов. В отличие от квант. электродинамики, здесь вместо одного заряж. лептона (напр., эл-на, мюона) выступают три кварка каждого типа, различающихся квант. числом «цвет». Переносчиками вз-ствия (вместо фотона в квантовой электродинамике) служат восемь «цветных» глюонов — безмассовых частиц со спином 1, источником которых явл. «цветовой заряд» квар­ков. Поскольку глюоны — «цветные», при их поглощении и испускании кварки меняют свой «цвет». Обла­дая «цветовым зарядом», глюоны (в отличие от фотонов, не имеющих электрич. заряда) должны испытывать самодействие. Поэтому в КХД в диаг­раммах Фейнмана появляются вер­шины типа рис. 9 (пунктирные линии соответствуют глюонам). Это при­водит к тому, что в разложении вер­шинной части по теории возмущений, кроме диаграмм, аналогичных диаг­раммам рис. 8, а — д квант. электро­динамики, появляются диаграммы с самодействием глюонов (рис. 10, е -— з; сплошные линии соответствуют квар­кам). Именно эти диаграммы обус­ловливают тот факт, что первый член разложения  по эфф. «цветовому за-



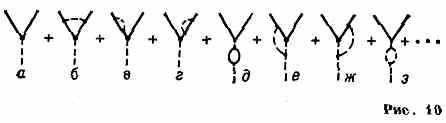
ряду» (т. е. по константе взаимодей­ствия) g оказывается отрицательным:



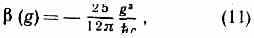
а вместо (10) получается выражение



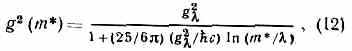
где g_ — величина эфф. заряда при яек-ром фиксированном значения m* = [т.е. g_=g(m*=], к-рое с ростом m* (с уменьшением рас­стояния) стремится к нулю. [Часто (12) записывают в виде g²/ћc=a._s(т*²)= 6/25ln (т*/), где  — некий

267


фундам. размерный параметр.│ Т. о., здесь появилась «антиэкранировка за­ряда»: ч-цы на малых расстояниях ста­новятся как бы свободными точеч­ными объектами. Это явление было на­звано асимптотической свободой. Оно наблюдается экспериментально в глу­боко неупругих процессах. В резуль­тате при больших передачах 4-пмпуль-са теория возмущений становится зам­кнутой: чем больше передача импуль­са, тем меньше эфф. константа раз­ложения g и тем больше основания для применения теории возмущений по такой константе.

С увеличением расстояния (уменьше­нием m*) эфф. заряду возрастает и фор­мально при m*==ехр(-6ћc/25g²) становится бесконечно большим: «цвет­ные» кварки и глюоны оказываются как бы заключёнными в «мешке» и не могут вылетать как свободные ч-цы (удержание «цвета»). Однако в этой области уже неправомерно пользовать­ся ни теорией возмущений для ф-ции (g), на основе к-рой было получено выражение (12), ни приближением одноглюонного обмена (типа рис. 2), описывающим вз-ствие двух кварков. Иных же методов пока нет, хотя поис­ки их продолжаются. Тем не менее одна из распространённых гипотез состоит в том, что эффект удержания «цвета» должен сохраниться и в точ­ном выражении для ф-ции (g).

Другие подходы. В связи с трудно­стями теории возмущений в КТП воз­никли и развиваются подходы, не связанные с разложением по кон­станте вз-ствия. К их числу относятся аксиоматич. подход (см. А ксиоматическая теория поля), для к-рого типичен тщат. анализ положений (аксиом), образующих матем. и физ. фундамент теории, и выделение из их числа наи­более «надёжных». Среди результатов этого подхода — доказательство те­оремы СРТ, строгое доказательство связи спина со статистикой, доказа­тельство дисперсионных соотношений для амплитуд разл. процессов, на основе эксперим. проверки которых удалось установить правильность ис­ходных аксиом вплоть до расстояний 5•10^-16 см.

Другим направлением выхода за рамки теории возмущений явл. т. н. партонная модель, к-рая возникает как асимптотич. св-во КТП в обла­сти больших передач импульса (>>1 ГэВ/с) (см. Партоны). Харак­терная черта этой модели — установ­ление взаимосвязи между разл. про­цессами. Напр., знание сечения глу­боко неупругого рассеяния эл-на (мю­она) на протоне позволяет предска­зать поведение сечения рождения пары e⁺e^-(⁺^-) в протон-протонном со­ударении.

Калибровочные симметрии и еди­ные теории поля. КТП оказалась наиболее адекватным аппаратом для по­нимания природы вз-ствия ч-ц и объединения всех видов вз-ствий. В фи­зике элем. ч-ц различают сильное, эл.-магн., слабое и гравитац. вз-ствия и соотв. классы ч-ц: адрона (т. е. барионы и мезоны) или образующие их кварки и глюоны, к-рые участвуют во всех видах вз-ствия, лептоны и промежуточные векторные бозоны, не участвующие только в сильном вз-ствии (нейтрино не участвуют так­же в эл.-магн. вз-ствии), фотон, участ­вующий только в эл.-магн. и гравитац. вз-ствиях, и гипотетич. гравитон, переносчик гравитац. вз-ствия. Каж­дая из этих групп ч-ц характеризу­ется своими специфич. законами сох­ранения. Так, сохраняется «цветовой» и электрич. заряды. С большой сте­пенью точности сохраняются барионный и лептонный заряды. Кроме того, приближённо сохраняются такие хар-ки сильного вз-ствия, как изотопич. спин, странность, «очарование», и т. д. В КТП каждому из этих законов со­хранения соответствует определённая симметрия ур-ний движения относи­тельно преобразований полей. Напр., ур-ния КХД одинаковы для кварков любого «цвета», ур-ния для лептонов (за исключением слагаемого, пропорц. массе) не меняются при замене волн. ф-ции эл-на на волн. ф-цию _e или на любую их суперпозицию и т. д. Каждую из этих симметрии по аналогии с квант. электродинамикой можно расширить до локальной ка­либровочной симметрии, допускающей переход к подобным суперпозициям отдельно в каждой точке простран­ства-времени. При этом ур-ния дви­жения свободных полей оказываются неинвариантными и необходимо вве­дение компенсирующих (калибровоч­ных) векторных Янга — Миллса по­лей, обмен квантами к-рых обуслов­ливает вз-ствие между соответствую­щими ч-цами, подобно тому, как обмен фотонами обусловливает эл.-магн. вз-ствие заряж. ч-ц. Как и для фото­на, массы покоя этих квантов для не­нарушенной, точной, симметрии долж­ны быть равны нулю. Пример таких квантов — глюоны в КХД.

Для лептонной симметрии, однако, кванты компенсирующих полей — промежуточные векторные бозоны W ⁺, W^- и Z° должны быть массивными, т. к. слабое вз-ствие проявляется лишь на очень малых расстояниях (<10^-15 см). По этой причине лептонная симметрия должна быть нарушен­ной. Обычно это т. н. спонтанное нарушение симметрии, при к-ром нарушается симметрия не ур-ний ноля, а их решений, описывающих физ. состояния ч-ц. Как и в слу­чае точной симметрии, теория оказы­вается ренормируемой, т. е. позво­ляет вычислять радиац. поправки к вероятностям физ. процессов.

Универсальный способ введения всех вз-ствий, основанный на калибровоч­ной симметрии, даёт возможность

их объединения. При этом различие в величинах вз-ствия обусловливается разными массами ч-ц — переносчи­ков вз-ствия. Так, в 60-х гг. была соз­дана единая теория слабых и эл.-магн. вз-ствий (см. Слабое взаимодействие). Характерная особенность этой схе­мы — предсказание существования W⁺, W^-, Z° с массами (в энергетич. ед.) ок. 80—90 ГэВ и т. н. скалярных ч-ц Хиггса (массы к-рых не предска­зываются теорией). Идёт интенсивная работа по включению в эту теорию и сильного вз-ствия путём «великого объединения» (Grand Unification) «цве­товой» и лептонной симметрии. Одним из предсказаний такой теории явл. несохранение барионного заряда и, как следствие, нестабильность про­тона (его время жизни оценивается в 10³⁰ —10³² лет). Расширение прин­ципа калибровочной симметрии до суперсимметрии, объединяющей в од­ном семействе ч-цы с разными спи­нами и статистиками, даёт надежду на включение в объединённую схему и гравитац. вз-ствия (т. н. теория су­пергравитации).

• Ф е й н м а н Р. Ф., Теория фундамен­тальных процессов, пер. с англ., М., 1978; его же, Квантовая электродинамика, пер. с англ., М., 1964; Вайнберг С., Единые теории взаимодействия элементарных частиц, «УФН», 1976, т. 118, в. 3, с. 505.

А. В. Ефремов.

КВАНТОВАЯ ХИМИЯ, область теор. химии, в к-рой идеи и методы квант. механики применяются к исследова­нию атомов, молекул и др. хим. объек­тов и процессов. Квантовомеханич. подход в химии чаще всего основыва­ется на Шредингера уравнении для атома, молекулы или совокупности атомов и молекул: H=E. Опера­тор Н (гамильтониан) учитывает как кинетич. энергию составляющих сис­тему ч-ц (ат. ядер и эл-нов), так и энергию их вз-ствия друг с другом и с внеш. полями. Решение ур-ння даёт значение полной энергии системы Е и её состояния — волновые ф-ции , к-рые зависят от пространств. и спи­новых координат всех ч-ц и с помощью к-рых можно в принципе рассчитать св-ва системы. Однако точные реше­ния найдены лишь для атома водорода (см. Квантовая механика), поэтому для решения конкретных задач К. х. разработан ряд приближённых ме­тодов.

Электронное строение молекул — гл. предмет К. х. Согласно адиабатич. приближению, движение эл-нов в ат. системах рассматривается при фиксиров. положениях ядер и описыва­ется электронной волн. ф-цией, за­висящей от координат эл-нов и ядер. Из неполных сведений о виде этой ф-ции можно вывести качеств. интер­претацию физ. св-в молекул и их спектров, а более точные вычисления позволяют получить количеств. ре­зультаты.

Основы квант. теории многоэлек­тронных систем были заложены в ра­боте нем. физика В. Гейзенберга, по-

268


священной атому гелия (1926), и работах нем. физиков В. Гейтлера (Хайтлер) и Ф. Лондона о молекуле водорода (1927). Они показали, что существо­вание, устойчивость и св-ва этих систем невозможно объяснить в рамках классич. представлений. В последую­щих исследованиях были развиты ме­тоды определения электронных волн. ф-ций для более сложных ат. систем. Наиболее важный из них — метод мол. орбиталей (МО) — рассматривает дви­жение валентных эл-нов молекулы в ноле всех остальных эл-нов и ядер атомов, входящих в молекулу. Волн. ф-ции при таком одноэлектронном приближении находят при решении ур-ния Шрёдингера вариац. методом, обычно по схеме самосогласованного по­ля.. Метод МО представляет собой упрощённый вариант более общего метода вз-ствия конфигураций, к-рый в принципе позволяет рассчитывать достаточно точные волновые ф-ции молекул.

Нахождение и использование даже простейших волновых ф-ций сопряжено с весьма трудоёмкими вычисле­ниями.

В ранних квантовохим. исследова­ниях применялись почти исключитель­но приближённые полуэмпирич. ме­тоды. В сочетании с возмущений тео­рией они развивались как искусство делать качеств. предсказания практи­чески без вычислений, основываясь на интуиции и аналогиях. Так были установлены принципы теории меж­атомных взаимодействий и межмоле­кулярных взаимодействий, разработа­ны основы мол. спектроскопии, созда­на качеств. теория строения и реакц. способности нек-рых типов органич. молекул.

Развитие вычислительной техники в 60-х гг. 20 в. изменило стиль и направ­ление квантовохим. исследований. Ста­ли быстро развиваться неэмпирич. методы расчёта молекул и количеств. варианты полуэмпирич. методов. Рас­чёт на ЭВМ электронного строения мо­лекул ср. размеров (20—30 эл-нов) производится уже с точностью, во мн. случаях достаточной для предсказа­ния геом. строения, физ. св-в и спектров таких молекул. Особенно важны квантовохим. методы расчёта при изучении не поддающихся эксперим. регистрации короткоживущих активных ч-ц и активированных ком­плексов.

На совр. этапе в К. х. наряду с традиц. расчётами электронных волн. ф-ций разрабатываются новые про­блемы и методы. Развивается квант. теория движения ядер в хим. систе­мах, рассматриваются системы, ме­няющиеся во времени — в условиях хим. реакций, фотовозбуждения и рас­пада и т. д. Успешное решение задач К. х. во многом зависит от развития методов квант. механики и статистич. физики так, что К. х. можно с основа­нием рассматривать как ветвь теор. физики.

КВАНТОВАЯ ХРОМОДИНАМИКА (КХД), квантовополевая теория силь­ного вз-ствия кварков и глюонов, по­строенная по образу квант. электроди­намики (КЭД) на основе «цветовой» калибровочной симметрии. В отли­чие от КЭД, фермионы в КХД имеют дополнит. степень свободы — квант. число, принимающее три значения и наз. «цветом». Такими фермионами явл. кварки. Кварк каждого типа («аромата» — u, d, s, с, b) может на­ходиться в трёх «цветовых» состоя­ниях, связанных друг с другом калиб­ровочными преобразованиями. Ана­логом электрич. заряда (источника эл.-магн. поля) в КХД явл. «цветовой заряд», к-рый порождает глюонное по­ле. Вз-ствие кварков осуществляется посредством обмена глюонными полями восьми «цветовых» разновидностей, иг­рающими роль компенсирующих (ка­либровочных) Янга — Миллса полей. В отличие от эл.-магн. поля, эти поля, являясь «цветными», обладают «цве­товым зарядом» и поэтому сами по­рождают глюонные поля и взаимо­действуют друг с другом. Вследствие этого ур-ния для глюонного поля (в отличие от Максвелла уравнений в вакууме) нелинейны. Квантами глюонных полей явл. глюоны — ч-цы со спином 1 и нулевой массой покоя. В кач-ве константы вз-ствия (кон­станты связи) выступает «цветовой заряд» кварков и глюонов.

В методе теории возмущений вз-ствие глюонов приводит к тому, что в Фейнмана диаграммах наряду с вершинами



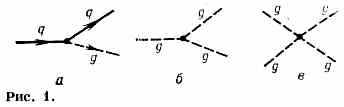
типа, изображённого на рис. 1, а, где кварк q (сплошная линия), испуская (или поглощая) глюон g (пунктирные линии), может изменить свой «цвет» (не меняя «аромата»), появляются вер­шины типа рис. 1, б, в, представляю­щие собой самодействие глюонов. Бла­годаря самодействию глюонов поля­ризация вакуума приводит к антиэк­ранировке «цветового» эффективного заряда g, т. е. к его убыванию с ро­стом квадрата переданного четырёх­мерного импульса (4-импульса) Q² (см. Квантовая теория поля):



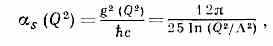
где  — некий фундам. размерный параметр теории. Сравнение с данными эксперимента показывает, что ве­личина  лежит в интервале 100— 300 МэВ/с. Это св-во т. н. асимптоти­ческой свободы позволяет доказать в КХД справедливость партонной кар­тины процессов с большой передачей 4-импульса (см. Партоны).

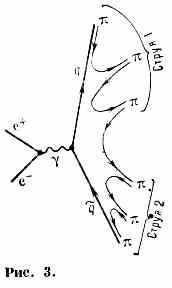
Однако благодаря вз-ствию между кварками и глюонами КХД вносит в эту картину ряд характерных элементов. К ним, например, относятся: а) определённый закон нарушения масштабной инвариантности в глу­боко неупругих процессах; б) опреде­лённое угл. распределение адронных струй, образующихся в процессе ан­нигиляции электрон-позитронной пары в адроны (рис. 3), и, в частности, появ­ление при высокой энергии трёхструйных процессов, связанных с испуска­нием жёсткого глюона кварком или антикварком, возникших при анни­гиляции е⁺е^-; в) трёхструйный хар-р распада ипсилон-частицы (=bb^~) че­рез трёхглюонную аннигиляцию bb^~; г) гораздо меньшая ширина распада векторных мезонов (напр., J/), чем псевдоскалярных или скалярных (напр., _с), поскольку первые рас­падаются с испусканием трёх глюо­нов (вероятность ~³_s), а вторые— двух (вероятность ~²_s), и ряд др. эффектов, получивших не только ка­чественное, но и количеств. подтвер­ждение в эксперименте. Всё это даёт



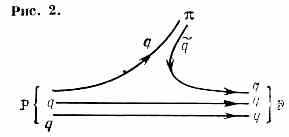
основание рассматривать КХД как динамику «цветных» кварков, свя­зывающую их в «бесцветные» адроны, т. е. как динамику сильного вз-ствия. Наиб. острая проблема КХД — причина отсутствия свободных квар­ков и глюонов. Она тесно связана с вопросом о том, как дальнодействующие силы между кварками (из-за обмена безмассо­выми глюонами) превращаются в короткодействую­щие яд. силы меж­ду адронами. Обычно считается, что по мере уда­ления «цветного» кварка, напр. в протоне (состоя­щем из трёх квар­ков), эфф. вз-ствие его возрастает на­столько, что из вакуума рождает­ся пара кварк-ан­тикварк, «обес­цвечивающая» как вылетающий кварк, так и остаток протона: кварк превращается в вир­туальный мезон (qq^~), ответственный за яд. силы (рис. 2). Аналогично объяс­няется и рождение адронных струй. Напр., в процессе аннигиляции пары е⁺е^- в адроны рождается пара «цвет­ных» qq^~, к-рая по мере разлёта рождает



269