От лат cavitas пустота), образование в капельной жидкости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац
| Вид материала | Документы |
- Вывихи. Переломы, 241.71kb.
- От лат evaporo испаряю и греч grapho пишу), метод получения изображений объектов, 2696.94kb.
- Реферат от лат rеfеrо "сообщаю", 198.27kb.
- Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
- Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
- Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
- Реферат от лат. «сообщать», 61.18kb.
- Лекция. Взаимосвязанные рынки, 285.49kb.
- Реферат Реферат, 36.91kb.
- Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.
Ближе к реальности модель, в к-рой молекулы рассматриваются как центры сил с потенциалом, зависящим от расстояния между ними. При этом дифференциальное эфф. сечение вз-ствия (для случая классич. механики) выражается через параметры столкновения b и : d=bdbd, где b — прицельное расстояние, — азимутальный угол линии центров. Для потенциала вз-ствия принимают обычно ф-ции простого вида, напр. const/rn (где n — нек-рая постоянная) или комбинацию подобных членов с разл. коэфф., к-рые учитывают притяжение молекул на больших расстояниях и
284
отталкивание на малых. Для квант. газов выражение для эфф. сечения получают на основе квант. механики, учитывая при этом влияние эффектов симметрии на вероятность столкновения (см. Кинетическое уравнение Больцмана). Методы решения кинетич. ур-ния были разработаны англ. учёным С. Чепменом и швед. учёным Ц. Энскогом.
К. т. г. позволяет исследовать: 1) смеси газов, когда для каждого компонента нужно вводить свою ф-цию распределения и рассматривать столкновения между молекулами разл. компонентов; 2) многоат. газы, когда нельзя рассматривать молекулу как матер. точку, а нужно учитывать её внутр. степени свободы (колебательные и вращательные); 3) плотные газы, когда нужно учитывать корреляции между сталкивающимися молекулами или многократные столкновения; 4) ионизов. газы (плазму), когда нельзя ограничиться учётом короткодействующих сил, а приходится также учитывать медленно убывающие с расстоянием кулоновские силы; это частично достигается введением самосогласованного поля; 5) разреженные газы, когда длина свободного пробега ч-ц сравнима с размерами системы и нужно учитывать столкновения со стенками.
• Больцман Л., Лекции по теории газов, пер. с нем., М., 1953; Чепмен С., К а у л и н г Т., Математическая теория неоднородных газов, пер. с англ., М., 1960; Боголюбов Н. Н., Проблемы динамической теории в статистической физике, М.—Л., 1946; Силин В. П., Введение в кинетическую теорию газов, М., 1971; Ф е р ц и г е р Дж., К а п е р Г., Математическая теория процессов переноса в газах, пер. с англ., М., 1976; Л и б о в Р., Введение в теорию кинетических уравнений, пер. с англ., М., 1974; Черчиньяни К., Теория и приложения уравнения Больцмана, пер. с англ., М., 1978; Климонтович Ю. Л., Кинетическая теория неидеального газа и неидеальной плазмы, М., 1975; Коган М. Н., Динамика разреженного газа. Кинетическая теория, М., 1967.
Д. Н. Зубарев.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, энергия механич. системы, зависящая от скоростей её точек. К. э. Т матер. точки равна: T=mv2/2, где m — масса этой точки, v — её скорость. К. э. механич. системы равна сумме К. э. всех её точек: T=mkv2k/2. Выражение К. э. системы можно ещё Представить в виде: Т=Mv2c/2+Тс, где М — масса всей системы, vc — скорость центра масс, Тс,— К. э. системы в её движении вокруг центра масс. К. э. тв. тела, движущегося поступательно, вычисляется так же, как К. э. точки, имеющей массу, равную массе всего тела. Ф-лы для вычисления К. э. тела, вращающегося вокруг неподвижной оси, см. в ст. Вращательное движение.
Изменение К. э. системы при её перемещении из положения 1 в положение 2 происходит под действием приложенных к системе внеш. и внутр. сил и равно сумме работ Aek и Aik этих
сил на данном перемещении: T2-T1=kAek+kAik. Это равенство выражает теорему об изменении К. э., с помощью к-рой решаются многие задачи динамики.
При скоростях, близких к скорости света, К. э. матер. точки равна:
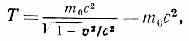
где m0 — масса покоящейся матер. точки, с — скорость света в вакууме (m0с2— энергия покоя точки). При малых скоростях (v<
• См. лит. при ст. Механика.
С. М. Тарг.
КИНЕТИЧЕСКИЕ КОЭФФИЦИЕНТЫ, входят в ур-ния термодинамики неравновесных процессов, определяющие зависимость потоков физ. величин (теплоты, массы компонентов, импульса и др.) от вызывающих эти потоки градиентов темп-ры, концентрации, гидродинамич. скорости и др. К. к. могут быть выражены через коэфф. теплопроводности, диффузии, вязкости и др., к-рые также наз. К. к. Вычисление К. к. на основе представления о мол. строении среды— задача кинетики физической, в частности кинетической теории газов (см. также Онсагера теорема).
Д. Н. Зубарев.
КИНЕТИЧЕСКИЙ МОМЕНТ, то же, что момент количества движения.
КИНЕТИЧЕСКИЙ ПОТЕНЦИАЛ, см. Лагранжа функция.
КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА, интегродифференциальное уравнение, к-рому удовлетворяют неравновесные одночастичные функции распределения систем из большого числа ч-ц, напр. ф-ция распределения f(v, r, t) молекул газа по скоростям v и координатам r, ф-ции распределения эл-нов в металле, фононов в кристалле и т. п. (см. Кинетика физическая). К. у. Б.— осн. ур-ние микроскопич. теории неравновесных процессов, физ. кинетики, в частности кинетической теории газов. К. у. Б. в узком смысле наз. кинетич. ур-ние для газов малой плотности. Различные обобщения К. у. Б., напр. для квазичастиц в кристаллах, для эл-нов в металле, также наз. К. у. Б., просто кинетич. ур-ниями или ур-ниями переноса.
К. у. Б. представляет собой ур-ние баланса числа ч-ц (точнее, точек, изображающих состояние ч-ц) в элементе фазового объема dvdr (dv=dvxdvydvz, dr=dxdydz) и выражает тот факт, что изменение ф-ции распределения ч-ц f(v, r, t) со временем t происходит вследствие движения ч-ц под действием внеш. сил и столкновений между ними. Для газа, состоящего из ч-ц одного сорта, К. у. Б. имеет вид:
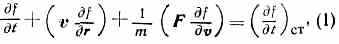
где f(v, r, t) dvdr — ср. число ч-ц в элементе фазового объёма dvdr около точки (v, r); F=F(r, t) — сила, действующая на ч-цу;(дf/дt)ст — изменение ф-ции распределения вследствие столкновении; дf/дt — изменение плотности
числа ч-ц около точки (v, r) в момент времени t за ед. времени. Второй и третий члены ур-ния (1) характеризуют соотв. изменение ф-ции распределения в результате перемещения ч-ц в пр-ве и действия внеш. сил. Её изменение, обусловленное столкновениями ч-ц, связано с уходом ч-ц из элемента фазового объёма при т. н. прямых столкновениях и пополнением объёма ч-цами, испытавшими «обратные» столкновения. Если рассчитывать столкновения по законам классич. механики и считать, что нет корреляции между динамич. состояниями сталкивающихся молекул, то в К. у. Б. (1)
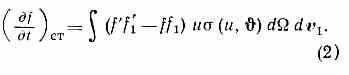
Здесь f(v, r, t) и f1(v1, r, t) — ф-ции распределения до столкновения, f' (v', r, t) и f'1(v'1, r, t) — после столкновения, v и v1— скорости ч-ц до столкновения, v', v'1— скорости тех же ч-ц после столкновения, u=│v-v1│ — модуль относит. скорости сталкивающихся ч-ц, — угол между относит. скоростью v-v1 сталкивающихся молекул и линией, соединяющей их центры, (u, ) d — дифференциальное эфф. сечение рассеяния ч-ц на телесный угол d в лаб. системе, зависящее от закона вз-ствия молекул. Для модели молекул в виде упругих жёстких сфер, имеющих радиус R, =4R2cos. К. у. Б. (1) было выведено австр. физиком Л. Больцманом (L. Boltzmann) в 1872.
К. у. Б. учитывает только парные столкновения между молекулами; оно справедливо при условии, что длина свободного пробега молекул значительно больше линейных размеров области, в к-рой происходит столкновение (для газа из упругих ч-ц сферич. формы это область порядка диаметра ч-ц). Поэтому К. у. Б. применимо для не слишком плотных газов. Иначе будет несправедливо осн. предположение об отсутствии корреляции между состояниями сталкивающихся молекул (гипотеза мол. хаоса). Если система находится в равновесии статистическом, то интеграл столкновений (2) обращается в нуль и решением К. у. Б. будет Максвелла распределение. Найденное для соответствующих условий решение К. у. Б. позволяет вычислить кинетические коэффициенты и получить макроскопич. ур-ния для
285
разл. процессов переноса (вязкости, диффузии, теплопроводности и др.). Для квант. газов значения эфф. сечений рассчитываются на основе квант. механики (с учётом неразличимости одинаковых ч-ц и того факта, что вероятность столкновения определяется не только хар-ром ф-ций распределения ч-ц до столкновения, но и хар-ром этих ф-ций после столкновения). Для фермионов учёт этих факторов приводит к уменьшению вероятности столкновений, а для бозонов— к увеличению. Интеграл столкновений в этом случае имеет более сложный вид (содержит ff1(1±f'1) (1± f'1) вместо ff1, где верхний знак относится К Ферми — Дирака статистике, а нижний — к Возе — Эйнштейна статистике). Ферми—Дирака распределение и Бозе — Эйнштейна распределение явл. решениями соответствующих квант. К. у. Б. для случая статистич. равновесия.
• См. лит. при ст. Кинетическая теория газов.
Д. Н. Зубарев.
КИНЕТОСТАТИКА (от греч. kinetos — движущийся и статика), раздел механики, в к-ром рассматриваются способы решения динамич. задач (особенно в динамике машин и механизмов) с помощью аналитич. или графич. методов статики. В основе К. лежит Д'Аламбера принцип, согласно к-рому ур-ния движения тел можно составлять в форме ур-ний статики, если к действующим на тело силам и реакциям связей присоединить силы инерции.
КИПЕНИЕ, переход жидкости в пар (фазовый переход I рода), происходящий с образованием в объёме жидкости пузырьков пара или заполненных паром полостей на нагреваемых поверхностях. Пузырьки растут (вследствие испарения в образующуюся полость жидкости), всплывают, и содержащийся в них насыщ. пар переходит в паровую фазу над жидкостью.
Для поддержания К. к жидкости необходимо подводить теплоту, к-рая расходуется на парообразование и на работу пара против внеш. давления при увеличении объёма паровой фазы (см. Испарение). Темп-pa, при к-рой происходит К. жидкости, находящейся под пост. давлением, наз. температурой кипения (Tкип). Строго говоря, Ткип соответствует темп-ре насыщ. пара (темп-ре насыщения) над плоской поверхностью кипящей жидкости, т. к. сама жидкость всегда несколько перегрета относительно Ткип. С ростом давления Tкип увеличивается (см. Клапейрона — Клаузиуса уравнение). Предельной темп-рой К. явл. критическая температура в-ва. Темп-pa К. при атм. давлении приводится обычно как одна из осн. физ.-хим. хар-к химически чистого в-ва.
При К. в жидкости устанавливается определ. распределение температуры
(рис. 1): у поверхностей нагрева (стенок сосуда, труб и т. п.) жидкость заметно перегрета. Величина перегрева зависит от ряда физ. и хим. св-в как самой жидкости, так и граничных тв. поверхностей. Опыты показывают, что тщательно очищенные жидкости, лишённые растворённых газов (воздуха),
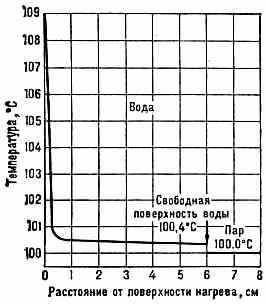
Рис. 1. Распределение темп-ры в жидкости над горизонт. поверхностью нагрева при пузырьковом кипении.
можно при соблюдении особых мер предосторожности перегреть на десятки градусов без закипания. Когда такая перегретая жидкость вскипает, то процесс К. протекает бурно, напоминая взрыв. Теплота перегрева расходуется на парообразование, поэтому закипевшая жидкость быстро охлаждается до темп-ры насыщ. пара, с к-рым она находится в равновесии. Возможность перегрева чистой жидкости без К. объясняется затруднённостью возникновения начальных маленьких пузырьков (зародышей): энергетич. затраты на образование пузырька значительны из-за большой поверхностной энергии пузырька. Если же жидкость содержит растворённые газы и разл. мельчайшие взвеш. ч-цы, то уже незначит. перегрев (на десятые доли градуса) вызывает устойчивое и спокойное К., при к-ром нач. зародышами паровой фазы служат газовые пузырьки, образующиеся на поверхности тв. ч-ц. Осн. центры парообразования находятся в точках нагреваемой поверхности, где имеются мельчайшие поры с адсорбиров. газом, а также разл. неоднородности, включения и налёты, снижающие мол. сцепление жидкости с поверхностью. Для роста образовавшегося пузырька необходимо, чтобы давление пара в нём несколько превышало сумму внеш. давления, давления вышележащего слоя жидкости и капиллярного давления, к-рое зависит от кривизны поверхности пузырька. Это условие осуществляется, когда пар и окружающая его жидкость, находящаяся с паром в тепловом равновесии, имеют темп-ру, превышающую Ткип. В повседневной практике наблюдается именно этот вид К., его наз. пузырьковым. Если повышать темп-ру поверхности нагрева Т (увеличивать температурный напор, измеряемый разностью Т-Tкип), то число центров парообразования резко возрастает, всё большее количество оторвавшихся пузырьков всплывает в жидкости, вызывая её интенсивное перемешивание. Это приводит к значит. росту теплового потока от поверхности нагрева к кипящей жидкости (росту теплоотдачи). Соотв. возрастает и кол-во образующегося пара.
При достижении максимального (критич.) значения теплового потока (для кипящей воды ~1500 кВт/м2 при T-Tкип=25—30°С) начинается второй, переходный режим К. При этом режиме теплоотдача и скорость парообразования резко снижаются, т. к. большая доля поверхности нагрева покрывается сухими пятнами из-за слияния образующихся пузырьков пара. Когда вся поверхность обволакивается тонкой паровой плёнкой, возникает третий, плёночный режим К., при к-ром теплота от раскалённой поверхности передаётся к жидкости через паровую плёнку путём теплопроводности и излучения. Все три режима К. можно наблюдать в обратном порядке, когда массивное металлич. тело погружают в воду для его закалки: вода закипает, охлаждение тела идёт вначале медленно (плёночное К.), потом скорость охлаждения начинает быстро увеличиваться (переходное К.) и
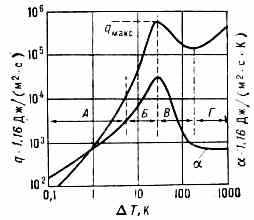
Рис. 2. Изменение плотности теплового потока q и коэфф. теплоотдачи . при кипении воды под атм. давлением в зависимости от температурного напора T: А — область слабого образования пузырьков; Б — пузырьковое кипение; В — плёночное кипение, постепенный переход к сплошной паровой плёнке; Г — стабильное плёночное кипение,qмакс — макс. значение q.
достигает наибольших значений в конечной стадии охлаждения (п у з ы р ь к о в о е К.). Теплоотвод в режиме пузырькового К. явл. одним из наиболее эфф. способов охлаждения (рис. 2).
Растворение в жидкости нелетучего в-ва понижает давление её насыщ. пара и повышает Tкип. Это позволяет определять мол. массу растворённых в-в по вызываемому ими повышению Ткип растворителя.
К. возможно не только при нагревании жидкости в условиях пост. давления. Снижением внеш. давления при пост. темп-ре можно также
286
вызвать перегрев жидкости и её вскипание (за счёт уменьшения темп-ры насыщения). Этим объясняется, в частности, явление кавитации — образование паровых полостей в местах пониж. давления жидкости (напр., в вихревой зоне за гребным винтом теплохода). Понижение Ткип с уменьшением внеш. давления лежит в основе определения барометрич. давления. К. при пониж. давлении применяют в холодильной технике, в физ. эксперименте (см. Пузырьковая камера) и т. д.
• К и к о и н А. К., Кикоин И. К., Молекулярная физика, 2 изд., М., 1976; Р а д ч е н к о И. В., Молекулярная физика, М., 1965; Михеев М. А., Основы теплопередачи, 3 изд., М.—Л., 1956, гл. 5; Скрипов В. П., Метастабильная жидкость, М., 1972.
КИРАЛЬНАЯ СИММЕТРИЯ в квантовой теории поля (КТП), симметрия ур-ний движения, к-рая комбинируется из двух разл. симметрии: симметрии вз-ствия адронов относительно обычных преобразований в «изотопич. пр-ве» (см. Изотопическая инвариантность) без изменения внутр. чётности и той же симметрии, но с изменением внутр. чётности. Т. о., преобразования К. с., кроме перемешивания состояний ч-ц с разл. электрич. зарядами, «перемешивают» и состояния с разной внутр. чётностью. К. с. явл. глобальной, т. е. не зависящей от точек пространства-времени. Такая инвариантность в случае ч-ц ненулевой массы не может быть связана ни с каким законом сохранения для фиксиров. системы ч-ц, а определяет лишь форму их вз-ствия, напр. форму вз-ствия нуклонов с псевдоскалярными пионами, испускание каждого из к-рых изменяет чётность системы. В этом смысле К. с. явл. динамич. симметрией. К. с.— один из примеров симметрии, приводящей к существенно нелинейной КТП (см. Нелинейная теория поля).
Инвариантность относительно вращений в «изотопич. пр-ве» без изменения чётности связана с законом сохранения векторных токов (V), а с изменением чётности — с законом сохранения аксиальных токов (А) (см. Ток). Сохранение векторного тока можно связать с сохранением полного электрич. заряда системы взаимодействующих ч-ц. В случае безмассовых спинорных (со спином 1/2) ч-ц, напр. нейтрино, сохранение аксиального тока можно связать с определ. законом сохранения — законом сохранения спиральности. Действительно, в случае безмассового спинорного поля, распространяющегося со скоростью света, спин квантов поля направлен либо против движения, либо в сторону движения. Соотв. различают левую и правую спиральности; 1-му случаю соответствует комбинация V-А токов частиц, 2-му — комбинация V+A, и эти комбинации должны сохраняться в отсутствие вз-ствия нейтрино с др. ч-цами. Однако если спинорная ч-ца имеет ненулевую массу
покоя, то её спин не обязательно должен быть ориентирован по оси движения. Но во вз-ствиях с др. ч-цами это кач-во спиральности опять проявляется. Так, в слабом взаимодействии участвуют только лептоны с левыми спиральностями, а в сильном могут участвовать как левые (с левой спиральностью ч-ц) токи адронов (V-А), так и правые (V+A).
Наряду с теорией поля, использующей лагранжев формализм с лагранжианами, удовлетворяющими требованиям К. с., для нахождения связей между вероятностями процессов с разл. числом взаимодействующих адронов используется т. н. а л г е б р а т о к о в— соотношения, связывающие коммутатор двух токов с самими токами. Она состоит из двух независимых алгебр: алгебры левых токов адронов (V-А) и алгебры правых токов адронов (V+A). Поскольку в этой теории имеется симметрия относительно правых и левых токов, данная симметрия и наз. киральной (от греч. cheir — рука).
Киральная КТП описывает многочисл. процессы рассеяния и распада адронов при низких энергиях в хорошем согласии с эксперим. данными. Она имеет место и при описании процессов при очень высоких энергиях (напр., в модели партонов).
К. с.— приближённая; она была бы точной, если бы масса псевдоскалярных пионов равнялась нулю. Поскольку же их масса отлична от нуля (хотя и существенно меньше массы барионов), аксиальные токи сохраняются лишь частично (степень несохранения пропорц. массе мезона, см. Аксиального тока частичное сохранение).
•Токи в физике адронов, пер. с англ., ПОД ред. Ю. В. Новожилова и Л. В. Прохорова, М., 1976; Волков М. К., П е р в у ш и н В. Н., Существенно нелинейные квантовые теории, динамические симметрии и физика мезонов, М., 1978.
М. К. Волков.
КИРХГОФА ЗАКОН ИЗЛУЧЕНИЯ, закон, утверждающий, что отношение испускат. способности (, Т) тел к их поглощат. способности а(, Т) не зависит от природы излучающего тела, равно излучат. способности абсолютно чёрного тела 0(, T) и зависит от длины волны излучения
и абс. темп-ры Т: ((, T))/((, T))=0(,T).
Ф-ция 0(, T) в явном виде даётся Планка законом излучения.
К. з. и. явл. одним из осн. законов теплового излучения и не распространяется на др. виды излучения. Он установлен нем. физиком Г. Р. Кирхгофом (G. R. Kirchhoff) в 1859 на основании второго начала термодинамики и затем подтверждён экспериментально. Согласно К. з. и., тело, к-рое при данной темп-ре лучше поглощает излучение, должно интенсивнее излучать. Напр., при накаливании платиновой пластинки, часть к-рой покрыта платиновой чернью, её чёрный конец (поглощат. способность к-рого близка к единице) светится ярче, чем светлый.