От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Капицы закон Капицы скачок температу­ры К. Н. Зиновьева. Кардинальные точки А' произ­вольной точки А Карно теорема Карно теорема Карно цикл Цикл Карно на диаграмме р — V (давление — объ­ём). Q Касательное ускорение М. П. Свиньин. Катодное падение Катодное пятно Катодное распыление Рис. 1. Зависимость коэфф. распыления К меди при облучении её пучком ионов Ar К — число ч-ц, испущенных мишенью, приходя­щихся на одну бомбардирующую ч-цу. При энергиях ξ Рис. 2. Зависимость коэфф. распыления К от Z материала мишени в случае ионов Kr Рис. 3. Зависимость к от угла падения  в случае крист. и аморфной германиевых ми­шеней, бомбардируемых ионами Ar Катодное тёмное простран­ство Э. А. Свириденкое. ... Полное содержание

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КАПИЦЫ ЗАКОН, эмпирич. правило, согласно к-рому электрич. сопротив­ление поликристаллич. образцов ме­таллов в сильном магн. поле растёт пропорц. напряжённости магнитного поля. Установлен П. Л. Капицей в 1928 для Cu, Au и Ag. Нашёл объясне­ние в теории гальваномагнитных яв­лений.

КАПИЦЫ СКАЧОК ТЕМПЕРАТУ­РЫ, открытое П. Л. Капицей (1941) явление в сверхтекучем жидком гелии, состоящее в том, что при передаче теплоты от тв. тела к жидкому гелию на границе раздела возникает раз­ность темп-р T. В дальнейшем было установлено, что К. с. т.— общее физ. явление при низких темп-pax: он возникает на границе раздела любых разнородных сред (из к-рых, по край­ней мере, одна — диэлектрик) при наличии теплового потока через гра­ницу (из одной среды в другую). Скачок темп-ры T прямо пропорц. плотности теплового потока Q и об­ратно пропорц. Т³:

T=RQ=(A/T²⁾Q,

где коэфф. А зависит от упругости находящихся в контакте в-в, а также от термич. и механич. обработки по­верхности.

На границе отожжённая медь — жидкий ⁴Не при темп-ре 0,1 К и Q=10^-4 Вт/м² T=2,4•10^-3 К. Т. о., R=2,4.10^-2/T³(м²•К/Вт). Для др. металлов (при тех же условиях) R имеет близкие значения. Величина R наз. сопротивлением Капицы или граничным тепловым сопротивлением.

Теоретически показано (И. М. Ха­латников, 1952), что при низких темп-pax теплообмен между жидкостью и тв. телом осуществляется посредством тепловых фононов, а К. с. т. на гра­нице возникает из-за различия акустич. импедансов двух сред. К. с. т. препятствует охлаждению тел до сверхнизких темп-р.

• Капица П. Л., Исследование механиз­ма теплопередачи в гелии II, «ЖЭТФ», 1941, т. 11, в. 1, с. 1; Халатников И. М., Теплообмен между твердым телом и гелием II, там же, 1952, т. 22, в. 6, с. 687; Н а г г i s о n J. P., Review Paper. Heat transfer bet­ween liquid helium and solids below 100 mK, «J. Low Temp. Phys.», 1979, v. 37, № 5/6, p. 467.

К. Н. Зиновьева.

КАПЛЯ, небольшой объём жидкости, ограниченный в состоянии равновесия поверхностью вращения. К. образую­тся при медленном истечении жидко­сти из небольшого отверстия или стекании её с края поверхности, при распылении жидкости и эмульгировании, а также при конденсации пара на тв. несмачиваемых поверхностях и в газовой среде на центрах конден­сации.

Форма К. определяется действием поверхностного натяжения и внеш. сил (напр., силы тяжести). Микроскопич. К., для к-рых сила тяжести не играет большой роли, а также К. в условиях невесомости имеют форму шара. Крупные К. в земных условиях имеют форму шара только при ра­венстве плотностей К. и окружающей среды. Падающие дождевые К. под действием силы тяжести, давления встречного потока воздуха и поверх­ностного натяжения сплюснуты с од­ной стороны. На смачиваемых поверх­ностях К. растекаются, на несмачи­ваемых — принимают форму сплюс­нутого шара (см. Смачивание). Форма и размер К., вытекающих из капилляр­ной трубки, зависит от её диаметра, поверхностного натяжения 0 и плот­ности жидкости, что позволяет по весу капель определять а.

• Г е г у з и н Я. Е., Капля, М., 1973.

КАРДИНАЛЬНЫЕ ТОЧКИ оптиче­ской системы, точки на оптич. оси ОО’ (рис.) центрированной оптич. си­стемы, с помощью к-рых может быть построено изображение произвольной точки пр-ва объектов в параксиальной области. Параксиальной наз. область около оси симметрии оптич. системы, где точка изображается точ­кой, прямая — прямой, а плоскость— плоскостью. К. т. оптич. системы служат четыре точки (рис.): передний F и задний F' фокусы, передняя H и задняя Н' главные точки. Задний

243


фокус явл. изображением беско­нечно удалённой точки, расположен­ной на оптич. оси в пр-ве объектов, а передний фокус — изображе­нием в пр-ве объектов бесконечно уда­лённой точки пр-ва изображений. Главные точки — это точки пересечения с оптич. осью главных плоскостей — плоскостей, вза­имное изображение к-рых оптич. система С даёт в натуральную величину (всякая точка h₁, расположенная в главной плоскости НH₁ на расстоянии h от оси OO', изображается в др. глав­ной плоскости Н'Н'₁ точкой Н'₁ на том же расстоянии h от оси, что и точ­ка H₁).




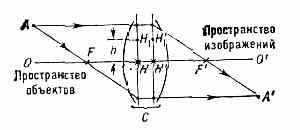
Расстояние от точки Н до точки F наз. передним фокусным расстоянием (отрицательным на рисунке, т. к. направление от Н до F против хода световых лучей), а расстояние от точки Н' до точки F' — задним ф о к у с н ы м р а с с т о я н и е м (положительным на рисунке, т. к. направление от Н' до F' совпа­дает с ходом лучей).

Построение изображения А' произ­вольной точки А центрированной оп­тич. системой с помощью К. т. пока­зано на рисунке. Луч, проходящий через передний фокус F, направляется системой параллельно её оптической осп ОО', а луч, падающий парал­лельно ОО' после преломления в си­стеме, проходит через её задний фо­кус F'.

• Тудоровский А. И., Теория опти­ческих приборов, 2 изд., [ч. 1], М.—Л., 1948.

Г. Г. Слюсарев.

КАРНО ТЕОРЕМА, теорема о макс. коэффициенте полезного действия теп­ловых двигателей (франц. физика Н. Л. С. Карно, N. L. S. Carnot; 1824): кпд =(T₁-T²)T₁ Карно цикла максимален и не зависит от природы рабочего в-ва и конструкции идеаль­ного теплового двигателя, он опре­деляется только темп-рами нагре­вателя t₁ и холодильника Т₂. К. т. сыграла важную роль в установлении второго начала термодинамики.

КАРНО ТЕОРЕМА в теории удара, теорема о потере кинетич. энергии при абсолютно неупругом ударе. Названа по имени франц. математика Л. Н. Карно (L. N. Carnot). Кинетич. энергия, потерянная системой при уда­ре, равна той кинетич. энергии, к-рую имела бы система, если бы её точки двигались с т. н. потерянными скоро­стями, т. е. T₀-t₁= ¹/₂_im_i(v_0i-v_1i)²,

где T₀=¹/₂_im_iv²_0i и T₁=¹/₂_im_iv²_1i—

кинетич. энергия системы соотв. в начале и в конце удара, m_i — масса i-той точки системы, v_оi и v_1i — ско­рости i-той точки в начале и в конце удара, (v_oi-v_1i) — т. н. потерянная скорость точки. К. т. явл. прямым следствием применения к явлению неупругого удара законов сохранения импульсов и энергии для изолирован­ной механич. системы. В ряде случаев К. т. позволяет определить скорости тел в конце неупругого удара.

КАРНО ЦИКЛ, обратимый круговой процесс, в к-ром совершается превра­щение теплоты в работу (или работы в теплоту). К. ц. состоит из последо­вательно чередующихся двух изотермич. и двух адиабатич. процессов, осуществляемых с рабочим телом (напр., паром). Впервые рассмотрен франц. физиком Н. Л. С. Карно (1824) как идеальный рабочий цикл теплового двигателя, совершающего работу за счёт теплоты, подводимой к рабочему телу в изотермич. процессе. Рабочее тело последовательно нахо­дится в тепловом контакте с двумя тепловыми резервуарами (имеющими постоянные темп-ры) — нагревателем (с темп-рой t_i) и холодильником



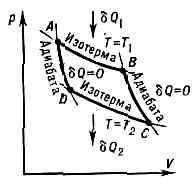
Цикл Карно на диаграмме р — V (давление — объ­ём). Q₁ — кол-во теплоты, полу­чаемой рабочим телом от нагрева­теля, Q₂—кол-во теплоты, отдавае­мой им холодиль­нику. Площадь, ограниченная изо­термами и адиаба­тами, численно равна работе цик­ла Карно.


(с T₂<t₁) . Превращение теплоты в работу сопровождается переносом ра­бочим телом определ. кол-ва теплоты от нагревателя к холодильнику. К. ц. осуществляется след. образом (рис.): рабочее тело (напр., пар в цилиндре под поршнем) при темп-ре Т₁ приво­дится в соприкосновение с нагрева­телем и изотермически получает от него кол-во теплоты Q₁ (при этом пар расширяется и совершает работу). На рисунке этот процесс изображён отрезком изотермы АВ. Затем рабочее тело, расширяясь адиабатически (по адиабате ВС}, охлаждается до темп-ры T₂ и приводится в тепловой контакт с холодильником. При этой темп-ре, сжимаясь изотермически (отрезок CD), рабочее тело отдаёт кол-во теплоты Q₂ холодильнику. Завершается К. ц. адиабатным процессом (отрезок DA), возвращающим рабочее тело в исход­ное термодинамич. состояние. При пост. разности темп-р (T₁-T₂) между нагревателем и холодильником рабочее тело совершает за один К. ц. работу

A=Q₁-Q₂=((T₁-T₂)/T₁)Q₁. Эта ра­бота численно равна площади АВCD, ограниченной отрезками изотерм и адиабат, образующих К. ц.

К. ц. обратим и его можно осуще­ствить в обратной последовательности (в направлении ADCBA). При этом кол-во теплоты Q₂ отбирается у хо­лодильника и передаётся нагревателю за счёт затраченной работы А. Теп­ловой двигатель работает в этом режи­ме как идеальная холодильная машина. К. ц. имеет наивысший кпд =/Q₁=(T₁-T₂)/Т₁ среди всех возможных циклов, осуществляе­мых в одном и том же температур­ном интервале (Т₁ -Т₂) (см. Карно теорема). В этом смысле кпд К. ц. служит мерой эффективности др. ра­бочих циклов.

Исторически К. ц. сыграл важную роль в развитии термодинамики и теплотехники. С его помощью была до­казана эквивалентность формулиро­вок К. Клаузиуса и У. Томсона (Кель­вина) второго начала термодинамики; К. ц. был применён для определения абс. термодинамич. шкалы темп-р (см. Температурные шкалы); часто ис­пользовался для вывода разл. термо­динамич. соотношений (напр., Кла­пейрона — Клаузиуса уравнение).

• Ф е р м и Э., Термодинамика, пер. с англ., Хар., 1969; К р и ч е в с к и й И. Р., По­нятия и основы термодинамики, М., 1962; Зоммерфельд А., Термодинамика и статистическая физика, пер. с нем., М., 1955.

КАСАТЕЛЬНОЕ УСКОРЕНИЕ, состав­ляющая ускорения, направленная по касательной к траектории.

КАСКАДНЫЙ ГЕНЕРАТОР, устрой­ство, преобразующее низкое перем. напряжение в высокое пост. напря­жение. В отд. каскадах перем. напря­жения выпрямляются, а выпрямлен­ные напряжения включаются последо­вательно и суммируются. Связь кас­кадов с источниками питания осуще­ствляется через ёмкости или посред­ством взаимной индукции. Питание каскадов может быть как носледовательным, так и параллельным.



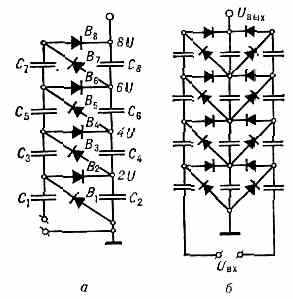
Рис. 1. Схемы каскадных генераторов с последоват. питанием на ёмкостях: о — не­симметричная (генератор Кокрофта — Уолтона); б — симметричная (генератор Халперна); С — ёмкости; В — электрич. вен­тили.


Среди ёмкостных К. г. с последоват. пита­нием наиболее распространены гене­ратор Кокрофта — У о л т о н а (впервые построен в 1932 англ. учёными Дж. Кокрофтом и Э. Уолтоном, рис. 1, а) и симметричный гене-

244


ратор Халперна (1955) (рис. 1, б). На каждом конденсаторе C₂, С₄, С₆, С₈ создаётся пост. разность потенциалов, равная удвоенной амплитуде входного напряжения U_вх, а благодаря последоват. соединению конденсаторов выходное напряжение U_вых равно сумме этих разностей потенциалов. Число каскадов ограни­чено ростом падения напряжения под



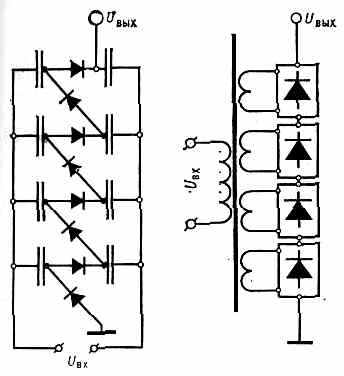
Рис. 2. Схемы генераторов с параллельным питанием каскадов: слева — с ёмкостной, справа — с индуктивной связью.




Рис. 3. Каскадный генератор на напряже­ние 2,5 MB мощностью 26 кВт (СССР).

нагрузкой (пропорц. третьей степени числа каскадов). Распространены также К. г. с параллельным питанием с ёмкостной (рис. 2, слева) и с индук­тивной (рис. 2, справа) связью. Кпд К. г. 70—80%, а у мощных К. г. с кремниевыми электрич. вентилями

может превышать 90%. Максимально достигнутое напряжение и мощность у ёмкостных К. г. ~5 MB и 200 кВт, у К. г. с индуктивной связью 3MB и 100 кВт. В СССР разработаны ём­костные К. г. с напряжением до 2,5 MB (рис. 3). Традиц. область применения К. г.— электрофиз. аппаратура, и в первую очередь высоковольтные уско­рители большой мощности. К. г. применяются также в электротехнике, рентг. аппаратуре, электронной мик­роскопии и др.

• Комар Е. Г., Основы ускорительной техники, М., 1975; Альбертинский Б. II., С в и н ь и н М. П., Каскадные ге­нераторы, М., 1980.

М. П. Свиньин.

КАТАДИОПТРИКА (от греч. katoptrikos — зеркальный, отражённый в зеркале и dioptrikos — относящийся к прохождению света сквозь прозрач­ную среду), историческое, ныне устар., название раздела геометрической оп­тики, в к-ром рассматривались оптич. системы, включавшие как зеркала, так и элементы с преломляющими свет поверхностями (линзы и др.), напр. зеркально-линзовые системы.

КАТОД (от греч. kathodes — ход вниз, возвращение; термин предложен англ. физиком М. Фарадеем в 1834), 1) от­рицательный электрод электроваку­умного или газоразрядного прибора, служащий источником эл-нов, к-рые обеспечивают проводимость межэлек­тродного пр-ва в вакууме или в газе. В зависимости от механизма испус­кания эл-нов различают термо­электронные катоды, фотокатоды и холодные К. 2) Отрицательный элек­трод источника тока (гальванич. эле­мента, аккумулятора и др.). 3) Элект­род электролитич. ванны, электрич. дуги и др. подобных устройств, при­соединяемый к отрицат. полюсу источ­ника тока.

КАТОДНОЕ ПАДЕНИЕ потенциала, разность потенциалов между катодом электрического разряда в газе и стол­бом плазмы. Чаще всего К. п. обус­ловлено избытком положит. ионов у катода, образующим положит. про­странств. заряд, к-рый экранирует катод. Однако в нек-рых видах несамостоят. электрич. тока в газе при интенсивной электронной эмиссии из катода возникает К. п., создаваемое отрицат. пространств. зарядом (из­быток эл-нов); такое К. п. ограничи­вает эмиссию и препятствует даль­нейшему увеличению пространств. заряда.

В зоне К. п. идут процессы первич­ной генерации эл-нов, обеспечиваю­щие протекание электрич. тока в газе: разл. эмиссии с поверхности катода (автоэлектронная эмиссия, термо­электронная эмиссия, взрывная элек­тронная эмиссия и т. п.), формирова­ние слоя, ускорение эл-нов, ионизация и т. д. Энергия, необходимая для протекания этих процессов, черпается за счёт К. п., изменяющегося в зави­симости от условий разряда от неск. В до 1 кВ. Отличия между разными формами газового разряда обусловлены в первую очередь особенностями и различиями этих прикатодных про­цессов. Конкретная величина К. п. зависит от рода газа, материала и формы катода и состояния его поверх­ности. К. п. не зависит от расстояния между электродами и от величины разрядного тока в широком интервале значений последнего.

КАТОДНОЕ ПЯТНО, ярко светящее­ся пятно на поверхности катода. Воз­никает при переходе тлеющего разряда к дуговому разряду вследствие измене­ния осн. механизма генерации эл-нов: в простейшем случае автоэлектронная эмиссия сменяется термоэлектронной эмиссией, зона эмиссии практически со всей поверхности катода стягива­ется в малое К. п., темп-pa в области к-рого резко увеличивается и дости­гает значений темп-ры плавления или возгонки. В зависимости от материала и геометрии катода и величины тока, помимо термоэмиссии, возможны и др. механизмы при переходе тлеющего разряда к дуговому (напр., взрывная электронная эмиссия, плазменный катод).

В. Н. Колесников.

КАТОДНОЕ РАСПЫЛЕНИЕ, разру­шение тв. тел при бомбардировке их поверхности атомами, нонами и нейт­ронами (впервые наблюдалось как разрушение катода в газовом разряде). Продукты распыления — атомы, положит. и отрицат. ионы, а также



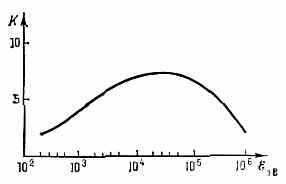
Рис. 1. Зависимость коэфф. распыления К меди при облучении её пучком ионов Ar⁺ от энергии ионов ξ.

нейтр. и ионизиров. ат. комплексы (кластеры). Скорость К. р. характери­зуют коэфф. распыления К — число ч-ц, испущенных мишенью, приходя­щихся на одну бомбардирующую ч-цу. При энергиях ξ бомбардирующих ч-ц ниже определ. порога ξ_п К=0. При ξ>ξ_п К возрастает, проходит через максимум (положение к-рого зависит от рода бомбардирующих ч-ц и в-ва мишени) и убывает (рис. 1). Зависимость К от ат. номера атомов мишени Z показана на рис. 2. Величи­на К зависит также от угла  падения ч-ц на мишень; при увеличении  К растёт, проходит через максимум и затем убывает. В случае монокрист. мишеней на фоне возрастания К. р. наблюдаются резкие его уменьшения, когда направления бомбардировки становятся параллельными кристаллографич. осям либо плоскостям с ма-

245


лыми индексами кристаллографиче­скими (рнс. 3). К. р. может зависеть также от состояния поверхности (раз­меров зёрен, текстуры и др.). В слу­чае поликрист. и аморфных мишеней

угл. распределение распылённого в-ва широкое. Если ξ не слишком мала, то угл. распределение слабо зависит от сор­та ч-ц, их энергии, направления бомбар­дировки и соответст­вует закону косинуса (число распылённых ч-ц пропорц. cos уг­ла их вылета). При высоких энергиях угл. распределение



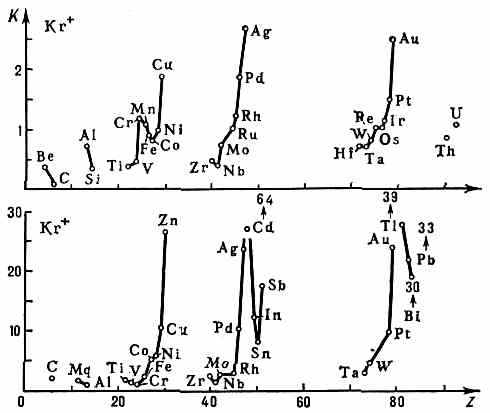
Рис. 2. Зависимость коэфф. распыления К от Z материала мишени в случае ионов Kr⁺ с энергией 400 эВ (вверху) и с энергией 45 кэВ (внизу).


более узкое, а при низких более широ­кое, чем даваемое законом косинуса. В случае монокрист. мишеней наблю­дается преимуществ. выход распылён­ного в-ва вдоль плотно упакованных осей мишени (эффект Венера).

Энергетич. спектр распылённых ч-ц широкий. Ср. энергии распылён­ных ч-ц тем меньше, чем больше коэфф. распыления.



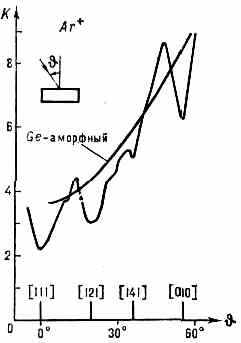
Рис. 3. Зависимость к от угла падения  в случае крист. и аморфной германиевых ми­шеней, бомбардируемых ионами Ar⁺ с энер­гией 30 кэВ.


Для монокрист. мишеней ср. энергия распылённых ч-ц также зависит от кристаллографич. направ­ления.

При бомбардировке атомами и иона­ми на поверхности мишени выявля­ются т. н. фигуры травления. Если облучение производится ионами газа, то в приповерхностном слое ми­шени могут образовываться пузырьки

газа, что приводит к вспучиванию поверхности (б л и с т е р и н г).

К. р. используется для обработки поверхностей, в т. ч. и для получения атомно-чистых поверхностей, для


анализа поверхностей методами ионно-ионной эмиссии, для получения тон­ких плёнок.

•Плешивцев Н. В., Катодное распы­ление, М., 1968; В е h r i s с h R., Sputtering by particle bombardment, В.—Hdlb.—N. Y., 1981.

В. Л. Молчанов.

КАТОДНОЕ ТЁМНОЕ ПРОСТРАН­СТВО, одна из осн. частей тлеющего разряда, в к-рой происходит ускорение эл-нов сильным электрич. полем.

КАТОДНЫЕ ЛУЧИ, поток эл-нов в тлеющем разряде столь низкого дав­ления, что значит. часть эл-нов, уско­ряясь в области катодного тёмного пр-ва, проходит практически весь разрядный промежуток. При падении на стеклянную стенку прибора К. л. вызывают флюоресценцию стекла. Термин «К. л.» почти не применяется.

КАТОДОЛЮМИНЕСЦЕНЦИЯ, лю­минесценция, возникающая при воз­буждении люминофора электронным пучком (катодными лучами); один из видов радиолюминесценции. Способ­ностью к К. обладают газы, мол. кристаллы, органич. люминофоры, кристаллофосфоры, однако только кристаллофосфоры стойки к действию электронного пучка и дают достаточ­ную яркость свечения и поэтому при­меняются в качестве катодолюминофоров.

К.возбуждается уже при энергиях эл-нов, в 1,5 раза превышающих иони­зационный потенциал атомов кристаллофосфора, однако для возбуждения К. обычно применяют пучки эл-нов с энергией выше 100 эВ. Эл-ны таких энергий преодолевают потенц. барьер, связанный с поверхностным зарядом кристалла, и выбивают вторичные эл-ны, к-рые в свою очередь ионизуют др. атомы крист. решётки люминофора. Этот процесс продолжается до тех пор, пока энергия вырываемых эл-нов достаточна для ионизации атомов.

Образовавшиеся в результате иониза­ции дырки мигрируют по решётке и могут передаваться центрам люминес­ценции. При рекомбинации на этих центрах дырок и эл-нов и возникает К. Спектр К. аналогичен спектру фотолюминесценции, её кпд обычно составляет 1—10% от энергии элект­ронного пучка, осн. часть к-рой пере­ходит в теплоту.

К. применяется в вакуумной элект­ронике (свечение экранов телевизо­ров, разл. осциллографов, электронно-оптич. преобразователей и т. д.). Яв­ление К. положено в основу создания лазеров, возбуждаемых электронным пучком.

• Москвин А. В., Катодолюминесценция, ч. 1—2, М.—Л., 1948—49; Электронно­лучевые трубки и индикаторы, пер. с англ., ч. 1 — 2, М., 1949 — 50.

Э. А. Свириденкое.