От лат cavitas пу­стота), образование в капельной жид­кости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац

Вид материала

Документы

Содержание Рис. 1, в. Микромонокристалл германия (увеличение в 4000 раз). Геометрия кристаллов. Рис. 3. Нитевидные кристаллы (электронно-микроскопич. изображение, увеличено в 3000 раз). Ge, тонких плёнок разл. полупроводников). Рис. 4. Монокристальная «буля» рубина (реальная дли­на 20 см). Атомная структура кристаллов. Параметры элементарной ячейки некоторых кристаллов Структура реальных кристаллов. Физические свойства кристаллов. Рис. 6. Нек-рые технически важные крис­таллы и изделия из них: кристаллы кварца, граната KDP и др., стержни рубина для ла­зеров, Критическая сила Е — модуль упругости материала, I Критическая температура Кривые равновесия жидкость — пар и критич. кривая (K Критическая точка. Критическая точка Параметры критической точки жидкость-пар некоторых веществ Критические явления Рис. 1. Изменение мольной магн. восприим­чивости  ферромагнетика (монокристалла Ni) с температурой T вблизи точки Кюри Т Рис. 2. Дисперсия (1) и поглощение (2) звука в Ar вблизи критич. темп-ры T ... Полное содержание

Подобный материал:

• Вывихи. Переломы, 241.71kb.
• От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов, 2696.94kb.
• Реферат от лат rеfеrо "сообщаю", 198.27kb.
• Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
• Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
• Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
• Реферат от лат. «сообщать», 61.18kb.
• Лекция. Взаимосвязанные рынки, 285.49kb.
• Реферат Реферат, 36.91kb.
• Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.

КРИСТАЛЛЫ (от греч. krystallos, первоначальное значение — лёд), твёрдые тела, обладающие трёхмерной периодич. ат. структурой и, при рав­новесных условиях образования, име­ющие естеств. форму правильных сим­метричных многогранников (рис. 1). К.— равновесное состояние твёрдых

327


тел. Каждому хим. в-ву, находяще­муся при данных термодинамич. ус­ловиях (темп-ре, давлении) в крист. состоянии, соответствует определён­ная атомно-крист. структура. К., вы­росший в неравновесных условиях и



Рис. 1, а. Природные кристаллы турмалина.



Рис. 1, б. Монокристалл сегнетовой соли.



Рис. 1, в. Микромонокристалл германия (увеличение в 4000 раз).


не имеющий правильной огранки (или потерявший её в результате обработ­ки), сохраняет осн. признак крист. состояния — решётчатую ат. струк­туру (кристаллическую решётку) и все определяемые ею св-ва.

Большинство тв. материалов явл. поликристаллическими; они состоят из множества отдельных беспорядоч­но ориентированных мелких крист.

зёрен (кристаллитов). Таковы, напр., многие горные породы, техн. ме­таллы и сплавы. Крупные одиночные кристаллы наз. монокристал­лами.

К. образуются и растут чаще всего из жидкой фазы — р-ра или расплава; возможно получение К. из газовой фазы или при фазовом превращении в тв. фазе (см. Кристаллизация). В при­роде встречаются монокристаллы разл. размеров — от громадных (до сотен кг) К. кварца (горного хрусталя), флю­орита, полевого шпата до мелких К. алмаза и др. Для науч. и пром. целей К. выращивают (синтезируют) в ла­бораториях и на заводах (см. Син­тетические кристаллы). К. обра­зуются и из таких сложных природ­ных в-в, как белки и даже вирусы (см. Биологические кристаллы).

Геометрия кристаллов. Выросшие в равновесных условиях К. имеют фор­му правильных многогранников той или иной симметрии, грани К.— пло­ские, рёбра между гранями — прямо­линейные, углы между соответствую­щими гранями К. одного и того же в-ва постоянны. Измерение межгранных углов (гониометрия) поз­воляет идентифицировать К. Ат. структура К. описывается как сово­купность повторяющихся в пр-ве оди­наковых элементарных ячеек, имею­щих форму параллелепипеда с рёб­рами а, b, с (периодами крист. решёт­ки). Всякая ат, плоскость крист. ре­шётки (к-рой может соответствовать грань К.) отсекает на осях координат целые числа периодов решётки (Гаюи закон). Обратные им числа (h, k, l) наз. индексами кристаллографическими граней и ат. плоскостей. Как пра­вило, К. имеет грани с малыми зна­чениями индексов, напр. (100), (110), (311). Длины рёбер а, b, с и углы , ,  между ними измеряются рентге­нографически. Выбор осей координат производится по определённым пра­вилам в соответствии с симметрией кристаллое.

По хар-ру симметрии любой крист. многогранник принадлежит к одному из 32 классов (или точечных групп симметрии), к-рые группируются в семь сингоний: триклинную, моноклинную, ромбическую (низшие сингонии), тетрагональную, гексагональную, тригональную (сред­ние) и кубическую (высшая).

Совокупность кристаллографически одинаковых граней (т. е. совмещаю­щихся друг с другом при операциях симметрии данной группы) образует т. н. простую форму К. Всего суще­ствует 47 простых форм К., но в каж­дом классе могут реализоваться лишь нек-рые из них. К. может быть огра­нён гранями одной простой формы (рис. 2, а), но чаще комбинацией этих форм (рис. 2, б, в).

Если К. принадлежит к классу, содержащему лишь простые оси сим­метрии (не содержащему плоскостей, центра симметрии или инверсионных

осей), то он может кристаллизоваться в зеркально разных формах — правой и левой (т. н. э н а н т и о м о р ф и з м).

Неравновесные условия кристалли­зации приводят к разл. отклонениям



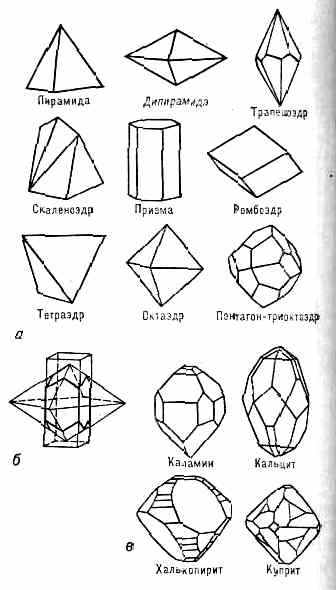
Рис. 2. а — нек-рые простые формы кристал­лов; б — комбинации простых форм; в — наблюдаемые огранки кристаллов.



Рис. 3. Нитевидные кристаллы (электронно-микроскопич. изображение, увеличено в 3000 раз).


формы кристалла от правильного мно­гогранника — к округлости граней и рёбер (вицинали), возникновению пла­стинчатых, игольчатых, нитевидных (рис. 3), ветвистых (дендритных) К. типа снежинок. Это используется в технике выращивания К. разнооб-

328


разных форм (дендритных лент Ge, тонких плёнок разл. полупроводников). Нек-рым К. уже в процессе вы­ращивания придаётся форма требуе­мого изделия — трубы, стержня (рис. 4), пластинки. Если в объёме



Рис. 4. Монокристальная «буля» рубина (реальная дли­на 20 см).


расплава образуется сразу большое число центров кристаллизации, то раз­растающиеся К., встречаясь друг с другом, приобретают форму непра­вильных зерен.

Атомная структура кристаллов. Ме­тоды структурного анализа К. (рентге­новский структурный анализ, элек­тронография, нейтронография) поз­воляют определить расположение атомов в элем. ячейке К. (расстояния между ними), параметры тепловых колебаний кристалла, распределение электронной плотности между атомами, ориентацию их магн. моментов и т. п.




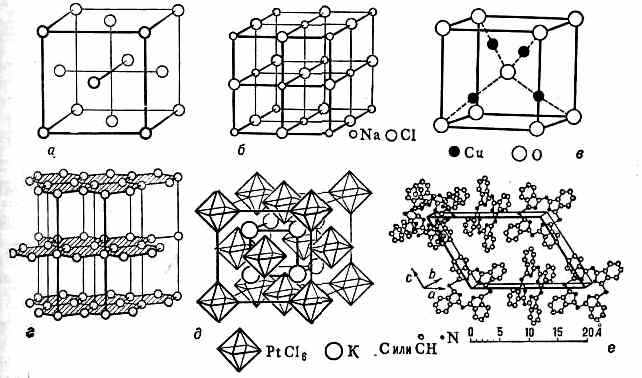
Рис. 5. Ат. структура меди (a), NaCl (б), CuO (в), графита (г), KPtCl₆ (д), фталоцианина (е).


ПАРАМЕТРЫ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ НЕКОТОРЫХ КРИСТАЛЛОВ



Уже изучена атомно-крист. структура более чем 30 тыс. соединений — от К. хим. элементов до сложнейших биол. К. (рис. 5, табл.).

Крист. структуры классифицируют по их хим. составу, в осн. определяющему тип хим. связи, по со­отношению компонент, по взаимной координации ато­мов (слоистые, цепные, кар­касные, координац. решёт­ки; см. Кристаллохимия). При изменении темп-ры или давления структура К. может изменяться. Нек-рые крист. структуры (фазы) явл. метастабильными. Существование у данного в-ва неск. крист. фаз наз. полиморфизмом. На­оборот, разные соединения могут иметь одинаковую крист. структуру (см. Изоморфизм).

Распределение К. по пространств. группам симметрии — соотв. по то­чечным группам (классам) и сингониям — неравномерно. Как правило, чем проще хим. ф-ла в-ва, тем выше сим­метрия его К. Так, почти все металлы

имеют кубическую или гексагональ­ную структуру, основанную на т. н. плотной упаковке атомов, то же от­носится к простым хим. соединениям, напр. к галогенидам щелочных метал­лов. Усложнение хим. ф-лы в-ва ве­дёт к понижению симметрии его К. Органические (молекулярные) К. поч­ти всегда относятся к низшим сингониям.

Тип хим. связи между атомами в К. определяет многие их св-ва. К о в а л е н т н ы е К. с локализованными на прочных связях эл-нами имеют вы­сокую твёрдость, малую электропро­водность, большие показатели пре­ломления. Металлич. К. с высокой концентрацией эл-нов проводимости хорошо проводят электрич. ток и теплоту, пластичны, непрозрачны (см. Металлы). Промежуточные хар-ки — у ионных К. Наиболее слабые (ван-дер-ваальсовы) связи — в молекулярных К. Они легкоплавки, механич. хар-ки их низки. Более низкую ат. упорядоченность, чем у К., имеют жидкие кристаллы и аморфные тела (см. Аморфное состояние, Неупорядо­ченные системы).

Структура реальных кристаллов. Вследствие нарушения равновесных условий роста и захвата примесей при кристаллизации, а также под влия­нием различного рода внеш. воздей­ствий идеальная структура К. всегда имеет те или иные нарушения. К ним относят точечные дефекты — ва­кансии, замещения атомов осн. ре­шётки атомами примесей, внедрение в решётку инородных атомов, дис­локации и др. (см. Дефекты в кри­сталлах). Дозируемое введение не­большого числа атомов примеси, за­мещающих атомы осн. решётки, ши­роко используется в технике для изменения св-в К., напр. введение в кристаллы Ge и Si атомов III и V групп периодич. системы элементов позволяет получать крист. полупро­водники с дырочной и электронной электропроводностями. Другие при­меры примесных кристаллов — рубин, состоящий из Al₂O₃ и примеси (0,05%) Cr; иттриево-алюминиевый гранат, состоящий из Y₃Al₅O₂ и примеси (до 1%) Nd.

При росте К. их грани по-разному захватывают атомы примесей. Это приводит к секториальному строению К. Может происходить и периодич. изменение концентрации захватывае­мой примеси, что даёт зонарную структуру. Кроме того, в процессе роста К. почти неизбежно образуются макроскопич. дефекты — включения, напряжённые области и т. п.

Все реальные К. имеют мозаичное строение: они разбиты на блоки моза­ики — небольшие (~10^-4 см) обла­сти, в к-рых порядок почти идеален, но к-рые разориентированы по отно­шению друг к другу на малые углы (приблизительно неск. минут).

Физические свойства кристаллов. Для К. данного класса можно указать симметрию его св-в. Так, кубич. К. изотропны в отношении прохождения света, электро- и теплопроводности, теплового расширения, но анизотроп­ны в отношении упругих, электрооптич., пьезоэлектрич. св-в. Наиболее анизотропны кристаллы низших сингоний (см. Кристаллофизика).

Все св-ва К. связаны между собой и обусловлены атомно-крист. структу­рой, силами связи между атомами и энергетич. спектром эл-нов (см. Зонная теория). Нек-рые св-ва, напр. тепло­вые, упругие, акустические, зависят непосредственно от межат. вз-ствий. Электрич., магн. и оптич. свойства существенно зависят от распределения эл-нов по уровням энергии. В нек-рых К. ионы, образующие решётку, рас­полагаются так, что К. оказывается

329


самопроизвольно поляризованным (пироэлектрики). Большая величина такой поляризации характерна для сегнетоэлектриков. Многие св-ва К. решающим образом зависят не только от симметрии, но и от кол-ва и типов дефектов (прочность и пластичность, окраска, люминесцентные св-ва и др.). В бездислокационных К. прочность в 10—100 раз больше, чем в обычных.

Применение. Многие монокристал­лы, а также поликрист. материалы имеют широкое практич. применение. Пьезо- и сегнетоэлектрич.. К. приме­няются в радиотехнике. Устройства полупроводниковой электроники (тра­нзисторы, ЭВМ, фотоприёмники и т. д.) основаны на полупроводниковых К. (Ge, Si, GaAs и др.) или микросхе­мах на них (см. Микроэлектроника).



Рис. 6. Нек-рые технически важные крис­таллы и изделия из них: кристаллы кварца, граната KDP и др., стержни рубина для ла­зеров, сапфировые пластины.


В запоминающих устройствах громад­ной ёмкости используются К. магнитодиолектриков и разл. типов ферри­тов. Исключит. значение имеют для квантовой электроники К. рубина, пттриево-алюминиевого граната и др. В технике управления световыми пуч­ками используют К., обладающие электрооптич. св-вами. Для измерения слабых изменений температуры при­меняются пироэлектрич. К., для из­мерения механич. и акустич. воздей­ствий — пъезоэлектрики, пьезомагнетики (см. Пъезомагнетизм) и т. п. Высокие механич. св-ва сверхтвёрдых К. (алмаз и др.) используются в об­работке материалов и в бурении; К. рубина, сапфира и др. служат опор­ными элементами в часах и др. точных приборах. Номенклатура пром. произ-ва разл. синтетич. кристаллов исчисляется тысячами наименований

(рис. 6).

• См. лит. при ст. Кристаллография.

Б. К. Вайнштейн, М. П. Шаскольская.

КРИТИЧЕСКАЯ СИЛА в теории упру­гости и теории пластичности, наимень­шая продольная сила, при к-рой в прямом брусе наступает потеря устой­чивости прямолинейной формы рав­новесия (см. Продольный изгиб). К. с.

зависит от механич. хар-к материала бруса, формы его поперечного сече­ния, условий закрепления, а при пластич. деформациях — ещё и от подат­ливости конструкции, элементом к-рой он является. К. с. упругого бруса определяется ф-лой Эйлера:



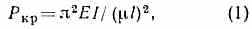
где Е — модуль упругости материала, I — наименьшее значение центр. мо­мента инерции поперечного сечения, l — длина бруса,  — коэфф., учи­тывающий условия закрепления. Напр., для бруса со свободно опёр­тыми концами =1; для бруса, один конец к-рого жёстко заделан, а дру­гой свободен, =2. При пластич. де­формациях пользуются ф-лой Карма­на; так, для бруса со свободно опёр­тыми концами

Р_кр =²K₁I/l², (2)

где k₁— модуль Кармана; для бруса прямоуг. сечения



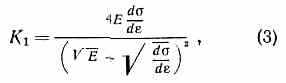
d/d — модуль упрочнения, к-рый определяется по экспериментальной зависимости между напряжением  и деформацией  при растяжении (сжа­тии).

И. В. Кеппен.

КРИТИЧЕСКАЯ ТЕМПЕРАТУРА, 1) теып-ра в-ва в его критическом сос­тоянии. Для индивидуальных в-в К. т. определяется как темп-pa, при к-рой исчезают различия в физ. св-вах между жидкостью и паром, находя­щимися в равновесии. При К. т. плот­ности насыщенного пара и жидкости становятся одинаковыми, граница между ними исчезает и теплота паро­образования обращается в нуль. К. т.— одна из физ.-хим. констант в-ва. Значения К. т. Т_к нек-рых в-в



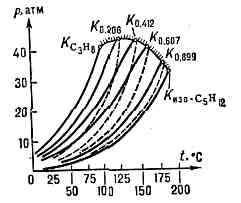
Кривые равновесия жидкость — пар и критич. кривая (K_С3H8 — К_{изо-С5H12}) системы пропан — изопентан при разл. концентра­ции изопентана.


приведены в ст. Критическая точка. В двойных системах (напр., пропан — изопентан, рис.) равновесие жид­кость — пар имеет не одну К. т., а пространственную критич. кривую, крайними точками к-рой явл. К. т. чистых компонентов. 2) Темп-pa, при к-рой в жидких смесях с ограниченно растворимыми компонентами насту­пает их взаимная неограниченная растворимость; её называют К. т. растворимости (см. рис. 3 в ст. Критическое состояние). 3) Темп-ра перехода ряда проводников в сверхпроводящее состояние (см. Сверхпро­водимость). Измерена у мн. металлов, сплавов и хим. соединений. В чистых металлах наинизшая К. т. обнару­жена у W (~0,01 К), наивысшая — у Nb (9,2 К). Очень высокое значение К. т. у Nb₃Ge (T_к23 К).

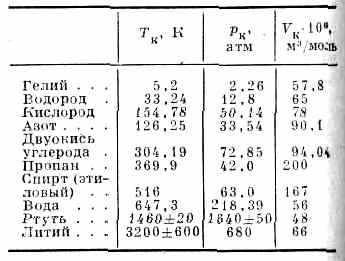
КРИТИЧЕСКАЯ ТОЧКА, точка на диаграмме состояния, соответствую­щая критическому состоянию. К. т. двухфазного равновесия жидкость — пар явл. конечной точкой на кривой испарения и характеризуется критич. значениями темп-ры T_к, давления р_к и объёма V_к (табл.).

ПАРАМЕТРЫ КРИТИЧЕСКОЙ ТОЧКИ ЖИДКОСТЬ-ПАР НЕКОТОРЫХ ВЕЩЕСТВ



К. т. представляет собой частный случай точки фазового перехода и характеризуется потерей термодинамич. устойчивости по плотности или составу в-ва. По одну сторону от К. т. в-во однородно (при Т>Т_к), а по другую (на кривой равновесия) — расслаивается на фазы. У смесей или р-ров следует различать К. т. рав­новесия жидкость — пар и К. т. рав­новесия фаз разл. состава, находящих­ся в одном агрегатном состоянии (т. н. критич. точка растворимости). В связи с этим К. т. смесей (р-ров) дополнительно характеризуется кон­центрацией х_к. В результате увеличе­ния числа параметров, определяющих состояние системы, у смесей имеется не изолированная К. т., а крити­ческая кривая, точки к-рой различаются значениями Т_к. р_к, V_к и х_к. В окрестности К. т. наблюдается ряд особенностей в поведении в-ва (см. Критические явления).

КРИТИЧЕСКИЕ ЯВЛЕНИЯ, специфич. явления, наблюдаемые вблизи критических точек и точек фазовых переходов II рода: рост сжимаемости в-ва в окрестности критич. точки рав­новесия жидкость — пар; .возраста­ние магн. восприимчивости и диэлектрич. проницаемости в окрест­ности Кюри точек Т_C ферромагне­тиков и сегнетоэлектриков (рис. 1); аномалия теплоёмкости в точке пере­хода гелия в сверхтекучее состояние (см. рис. в ст. Сверхтекучесть); за-

330


медление взаимной диффузии в-в вблизи критич. точек расслаивающих­ся жидких смесей; аномалии в рас­пространении ультразвука, рассея­нии света и др.

К К. я. в более узком смысле относят явления, обязанные своим про­исхождением росту флуктуации плот­ности, концентрации и др. физ. величин вблизи точек фазовых перехо­дов.



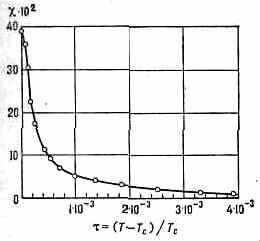
Рис. 1. Изменение мольной магн. восприим­чивости  ферромагнетика (монокристалла Ni) с температурой T вблизи точки Кюри Т_C ( — безразмерный параметр, характе­ризующий степень приближения к точке Кюри).


Значит. рост флуктуации при­водит к тому, что, напр., в критич. точке равновесия жидкость — пар плотность в-ва от точки к точке замет­но меняется. Возникшая неоднород­ность существенно влияет на физ. свой­ства в-ва, в нём, напр., усиливается рассеяние и поглощение излучений. Вблизи критич. точки жидкость — пар размеры флуктуации плотности доходят до тысяч А и сравниваются с длиной световой волны. В результате в-во становится совершенно непроз­рачным, б. ч. падающего света рас-



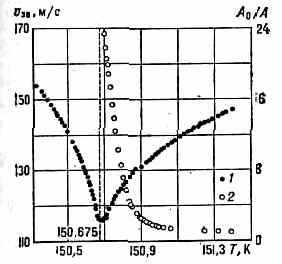
Рис. 2. Дисперсия (1) и поглощение (2) звука в Ar вблизи критич. темп-ры T_к перехода жидкость — пар (А — интенсивность зву­ка, прошедшего через в-во, А₀ — первонач. интенсивность звука, v_зв — скорость звука).


свивается, и в-во приобретает опало­вую (молочно-мутную) окраску — на­блюдается т.н. критическая о п а л е с ц е н ц и я. Рост флуктуа­ции плотности приводит также к дис­персии звука и его сильному погло­щению (рис. 2), замедлению установ­ления теплового равновесия (в кри­тич. точке оно устанавливается в те­чение многих часов), изменению хар-ра броуновского движения, аномалиям вяз­кости, теплопроводности и др.

Аналогичные явления наблюдаются вблизи критич. точек двойных (би­нарных) смесей; здесь они обусловле­ны развитием флуктуации концен­трации одного из компонентов в дру­гом. Так, в критич. точке расслоения смеси двух жидких металлов (напр.,



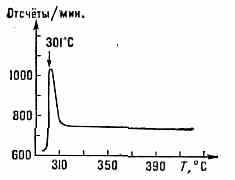
Рис. 3. Температурная зависимость рассея­ния рентг. лучей смесью жидких металлов Li и Na. Вблизи критич. точки растворимости смеси (301°С) число квантов рассеянного рентг. излучения, зафиксированных счёт­чиком в ед. времени, имеет резкий максимум.


Li—Na, Ge—Hg) наблюдается критич. рассеяние рентг. лучей (рис. 3). При упорядочении сплавов (напр., гид­ридов металлов) и установлении ориентационного дальнего порядка (см. Дальний и ближний порядок) в мол. кристаллах (напр., в твердых СН₄, ССl₄, галогенидах аммония) также на­блюдаются типичные К. я., связан­ные с ростом флуктуации соответ­ствующей физ. величины (упорядо­ченности расположения атомов спла­ва или ср. ориентации молекул по кристаллу) в окрестности точки фа­зового перехода.

Сходство К. я. в объектах разной природы позволяет рассматривать их с единой точки зрения. Установлено, напр., что у всех объектов существует одинаковая температурная зависи­мость ряда физ. св-в вблизи точек фазовых переходов II рода. Для полу­чения такой зависимости физ. св-во выражают в виде степенной ф-ции от приведённой темп-ры =(T-Т_к)/Т_к (здесь Т_к — критическая температу­ра) или др. приведённых величин (см. Приведённые параметры состояния). Напр., сжимаемость газа (дV/др)_Т, восприимчивость ферромагнетика (дМ/дН)_р,Т или сегнетоэлектрика (дDlдE)_p,T и аналогичная величина (дx/д)_p,T для смесей с критич, точ­кой равновесия жидкость — жидкость или жидкость — пар одинаково за­висят от темп-ры вблизи критич. точ­ки и могут быть выражены однотип­ной ф-лой:

(дV/др)_T, (дМ/дН)_р,T, (дD/дЕ)_р,T, (дх/д)_р,T~^-. (1)

Здесь V, р, Т — объём, давление и темп-pa, М и D — намагниченность и поляризация в-ва, Н и Е —напря­жённости магн. и электрич. полей,  — химический потенциал компо­нента смеси, имеющего концентра­цию х. Критич. индекс  имеет, по-видимому, одинаковые или близкие значения для всех систем. Экспери­менты дают значения , лежащие между 1 и ⁴/₃, однако погрешности в определении у часто оказываются того же порядка, что и различие резуль­татов экспериментов. Аналогична за­висимость теплоёмкости с от т для всех перечисл. систем, включая теп­лоёмкость гелия в точке перехода в сверхтекучее состояние (в -точке):



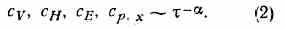
Значения а лежат в интервале между нулём и 0,2, во многих эксперимен­тах значение , оказалось близким к ¹/₈. Для -точки гелия =0 , и ф-ла (2) для гелия видоизменяется: с_p~ln.

Подобным же образом (в виде сте­пенного выражения) в окрестности критич. точки может быть выражена зависимость уд. объёма газа от дав­ления, магн. или электрич. момента системы от напряжённости поля, кон­центрации смеси от хим. потенциала компонентов. Константы ,  и др., характеризующие поведение всех физ. величин вблизи точек фазового пере­хода II рода, наз. критически­ми индексами.

В нек-рых объектах, напр. в обыч­ных сверхпроводниках и мн. сегне­тоэлектриках, почти во всём диапазо­не темп-р вблизи критич. точки К. я. не обнаруживаются. С другой сторо­ны, они оказывают влияние на в-ва обычных жидкостей в окрестности критич. точки в значит. диапазоне темп-р и на св-ва гелия вблизи -точки. Это связано с хар-ром действия межмолекулярных сил. Если эти силы достаточно быстро убывают с расстоя­нием, то в в-ве значит. роль играют флуктуации и К. я. возникают задол­го до подхода к критич. точке. Если же, напротив, молекулы взаимодей­ствуют на значит. расстояниях, что характерно, напр., для кулоновского и диполь-дипольного вз-ствий в сегнетоэлектриках, то установившееся в в-ве ср. силовое поле почти не будет искажаться флуктуациями и К. я. мо­гут обнаружиться лишь предельно близко к точке Кюри.

К. я. — это кооперативные явле­ния, они обусловлены св-вами всей совокупности ч-ц, а не индивидуаль­ными св-вами каждой ч-цы. Проблема кооперативных явлений полностью ещё не решена, поэтому нет и исчерпыва­ющей теории К. я. В существующих подходах к теории К. я. исходят из эмпирич. факта возрастания неодно­родности в-ва с приближением его к критич. точке и вводят понятие ра­диуса корреляции флуктуации r_c, близкое по смыслу к ср. размеру флук­туации. Радиус корреляции характе­ризует расстояние, на к-ром флуктуа­ции влияют друг на друга и, т. о., оказываются зависимыми, «скоррелированными». Этот радиус для всех

331


в-в зависит от темп-ры по степенному закону:

r_c ~ ^-v. (3) Предполагаемые значения v лежат между ¹/₂ и ²/₃.

Из ф-л (1), (2) и (3) видно, что зна­чения соответствующих величин ста­новятся бесконечно большими в точ­ках, где r_с обращается в бесконеч­ность (r_с неограниченно растёт при 0, т. е. с приближением к точке фазового перехода). Это означает, что любая часть рассматриваемой систе­мы в точке фазового перехода «чув­ствует» изменения, произошедшие с остальными частями. Наоборот, вдали от точки перехода флуктуации стати­стически независимы, и случайные из­менения состояния в-ва в данной точ­ке образца не сказываются на осталь­ном в-ве. Наглядным примером слу­жит рассеяние света в-вом. В случае рассеяния света на независимых флуктуациях (т. н. рэлеевское рассеяние) интенсивность рассеянно­го света обратно пропорц. ⁴ ( — длина волны) и прибл. одинакова по разным направлениям (рис. 4, а). При



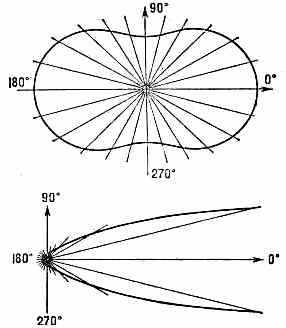
Рис. 4. Вверху —диаграмма направленности рассеяния света на независимых флуктуациях плотности жидкости; внизу — рассея­ние света на скоррелированных флуктуациях (рассеяние при критич. темп-ре).


рассеянии же на скоррелированных флуктуациях (т. н. критич. рассея­ние) интенсивность рассеянного света пропорц. ² и обладает особой диаг­раммой направленности (рис. 4, б). Большое распространение получила теория К. я., рассматривающая в-во близ точки фазового перехода как систему флуктуирующих областей раз­мером ~r_с. Она наз. теорией масш­табных преобразований (с к е й л и н г - т е о р и е й) или теорией по­добия. Скейлинг-теория не позволяет прямым образом вычислить критич. индексы, она лишь устанавливает меж­ду ними определ. соотношения, на ос­нове к-рых можно вычислить все индексы, если известны к.-н. два из них. Соотношения между критич. индексами позволяют определить уравне­ние состояния и вычислять затем разл. термодинамич. величины по сравни­тельно небольшому объёму эксперим. материала. На аналогичном принципе построена теория, связывающая не­сколькими соотношениями критич. ин­дексы кинетич. св-в (вязкости, тепло­проводности, диффузии, поглоще­ния звука и др., также имеющих ано­малии в точках фазовых переходов) с индексами термодинамич. величин. Эта теория наз. д и н а м и ч е с к и м с к е й л и н г о м в отличие от тео­рии статич. скейлинга, к-рая отно­сится только к термодинамич. св-вам материи.

• Ф и ш е р М., Природа критического со­стояния, пер. с англ., М., 1968; П о к р о в с к и й В. Л., Гипотеза подобия в теории фазовых переходов, «УФН», 1968, т. 94, в. 1: Critical phenomena, Wash., 1966; Стенли Г., Фазовые переходы и критические явле­ния, пер. с англ., М., 1973; Анисимов М. А., Исследования критических явлений в жидкостях, «УФН», 1974, т. 114, в. 2, с. 249; Паташинский А. З., Покров­ский В. Л., Флуктуационная теория фа­зовых переходов, М., 1975; Гинзбург В. Л., Л е в а н ю к А. П., С о б я н и н А. А., Рассеяние света вблизи точек фазо­вых переходов в твердом теле, «УФН», 1980, т. 130, в. 4.

В. Л. Покровский.