От лат cavitas пустота), образование в капельной жидкости полостей, заполненных газом, паром или их смесью (т н. кавитац пузырьков или каверн). Кавитац
| Вид материала | Документы |
- Вывихи. Переломы, 241.71kb.
- От лат evaporo испаряю и греч grapho пишу), метод получения изображений объектов, 2696.94kb.
- Реферат от лат rеfеrо "сообщаю", 198.27kb.
- Абсцесс и гангрена легкого определение заболевания острый абсцесс легкого, 403.26kb.
- Перелом подвздошной кости; перелом вертлужной впадины; перелом лобковой кости; открытая, 1124.91kb.
- Вишнев В. Н. Безродная Н. В. Остеохондроз Профилактика и лечение Введение, 623.65kb.
- Реферат от лат. «сообщать», 61.18kb.
- Лекция. Взаимосвязанные рынки, 285.49kb.
- Реферат Реферат, 36.91kb.
- Предыстория или как мне удалось получить музыкальное образование и чем это обернулось, 2157.21kb.
КОМПЛЕКСНАЯ АМПЛИТУДА, представление амплитуды А и фазы гармонич. колебания х=Аcos(t+) с помощью комплексного числа А~=Aехрi=A(cos+isin). При этом гармонич. колебание описывается выражением x=Re[A~exp(it)], где Re — веществ. часть комплексного числа, стоящего в квадратных скобках. Введение К. а. в теории колебаний позволяет перейти от дифф. ур-ний к алгебраическим. В случае перем. тока связь между К. а. тока и напряжения для активного сопротивления R определяется законом Ома: I~=U~/R; для индуктивности L: I~=U~/iL, a для ёмкости С: I~=U~•iС. Величины iL и 1/iC играют роли индуктивного и ёмкостного сопротивлений. К. а. тока для участка электрич. цепи, содержащего элементы L, С и R, на к-рый действует внешняя гармонич. эдс частоты , определяется соотношением I~=U~/Z. Здесь Z=R+i(L-1/C)—комплексное сопротивление участка цепи.
К. а. тока позволяет определить амплитуду и фазу реального тока в цепи.
КОМПЛЕКСНЫХ УГЛОВЫХ МОМЕНТОВ МЕТОД, то же, что Редже полюсов метод.
КОМПОНЕНТЫ (от лат. componens, род. падеж componentis — составляющий) в термодинамике, химически индивидуальные в-ва, из к-рых состоит термодинамич. система и к-рые могут быть выделены из системы и существовать вне её. Числом независимых К. наз. не общее число составляющих систему в-в, а наименьшее их число, достаточное для построения любой фазы системы. Так, в системе из СаО и СО2 образуется СаСO3 по реакции СаО+СO2СаСО3. Здесь за независимые К. можно принять СаО и СO2, а СаСО3 рассматривать как продукт их соединения. С равным правом К. можно считать СаО и СаСО3, а СО2— продуктом термич. диссоциации СаСО3. Независимые К. часто наз. просто К.
Для независимых К. характерно то, что масса каждого из них в системе не зависит от массы других. Поэтому в хим. системах (в к-рых составляющие в-ва вступают в хим. реакции) число независимых К. определяется разностью между числом составляющих в-в и числом независимо протекающих хим. реакций. Систему, в к-рой в-ва не реагируют друг с другом, наз. физической (напр., жидкая смесь бензол—глицерин), для неё число К. равно числу составляющих в-в. В зависимости от числа К. различают системы однокомпонентные, двухкомпонентные (двойные системы), трёхкомпонентные (тройные системы) и многокомпонентные (см. Гиббса правило фаз). Понятие «К.» было введено в 1875—76 амер. физиком Дж. У. Гиббсом.
в Г и б б с Дж. В., Термодинамические работы, пер. с англ., М.—Л., 1950, с. 104; Курс физической химии, под ред. Я. И. Герасимова, 2 изд., т. 1, М., 1969, с. 331; Исаев С. И., Курс химической термодинамики, М., 1975.
КОМПТОНА ЭФФЕКТ (комптон-эффект), упругое рассеяние эл.-магн. излучения на свободных (или слабо связанных) эл-нах, сопровождающееся увеличением длины волны; наблюдается при рассеянии излучения малых длин волн — рентгеновского и -излучений. Открыт в 1922 амер. физиком А. Комптоном (A. Compton) при исследовании рассеяния рентг. лучей в парафине. В К. э. впервые во всей полноте проявились корпускулярные св-ва эл.-магн. излучения (в частности, света).
Согласно классич. теории рассеяния света (развитой англ. физиком Дж. Томсоном), длина световой волны при рассеянии не должна меняться: под действием периодич. электрич. поля световой волны эл-н колеблется с частотой поля и поэтому излучает вторичные (рассеянные) волны той же частоты.
Первоначальная теория К. э. на основе квант. представлений была дана
Комптоном и независимо от него голл. физиком П. Дебаем. По квант. теории, световая волна представляет собой поток световых квантов — фотонов. Каждый фотон имеет определённую энергию ξ=h=hc/ и импульс p=(h/)n, где и — длина волны в частота падающего света, n — единичный вектор в направлении распространения волны. К. э. в квант. теории выглядит как упругое столкновение двух ч-ц — налетающего фотона и покоящегося эл-на. В каждом акте столкновения соблюдаются законы сохранения энергии и импульса. Фотон передаёт часть своей энергии и импульса эл-ну и изменяет направление движения — рассеивается; уменьшение энергии фотона и означает увеличение длины волны рассеянного света. Эл-н, получивший от фотона энергию и импульс, приходит в движение — испытывает отдачу. Направления движения ч-ц после столкновения и их энергии определяются законами сохранения энергии и импульса. (Т. к. при рассеянии фотонов высокой энергии эл-в отдачи может приобрести значит. скорость, необходимо учитывать релятив. зависимость энергии и импульса эл-на от его скорости.) Рис. 1 иллюстрирует закон сохранения импульса при К. э. Совместное решение ур-ний, выражающих законы сохранения энергии и импульса при К. э., даёт для сдвига длины световой волны ф-лу Комптона:
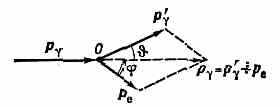
Рис. 1. Упругое столкновение фотона и эл-на в комптон-эффекте. До столкновения эл-н покоится. р и p' — импульсы налетающего и рассеянного фотонов; рe— импульс эл-на отдачи; — угол рассеяния фотона; — угол, под к-рым летит эл-н отдачи относительно направления падающего фотона.
='-= 0(1-cos). (1) Здесь '— длина волны рассеянного света, — угол рассеяния фотона, а 0=h/mec2,426•10-10 см 0,024 Å— т. н. комптоновская длина волны эл-на (mе— масса покоя эл-на). Из ф-лы (1) следует, что не зависит от длины волны падающего света, а определяется лишь углом и максимален при =180° (при рассеянии назад): макс= 20. Из этих же ур-ний можно получить выражение для энергии ξе эл-на отдачи («комптоновского» эл-на) в зависимости от угла его вылета . Эл-ны отдачи всегда имеют составляющую скорости по направлению движения падающего фотона (т. е. <90°).0пыт подтвердил предсказанную зависимость от и наличие эл-нов отдачи. Т. о. экспериментально была доказана правильность корпускулярных представлений о механизме К. э. и тем
306
самым — правильность исходных положений квант. теории.
В реальных опытах по рассеянию фотонов в-вом эл-ны не свободны, а связаны в атомах. Если ξ велика по сравнению с энергией связи эл-нов в атоме (ξсв), то рассеяние происходит, как на свободных эл-нах. Если же ξ недостаточна для того, чтобы вырвать эл-н из атома, то фотон обменивается энергией и импульсом с атомом в целом. Т. к. масса атома очень велика (по сравнению с эквивалентной массой фотона ξ/c2), то отдача практически отсутствует и рассеяние фотонов происходит без изменения их энергии, т. е. без изменения длин волн,— когерентно. В тяжёлых атомах лишь периферич. эл-ны связаны слабо, поэтому в спектре рассеянного излучения присутствует как
смещённая, комптоновская, линия от рассеяния на таких эл-нах, так и несмещённая линия от рассеяния на атоме в целом.
Рассмотренная упрощённая теория К.э. не позволяет вычислить все хар-ки комптоновского рассеяния, в частности интенсивность рассеяния фотонов под разными углами. Полную теорию К. э. даёт квантовая электродинамика. В этой теории К. э. представляется так: эл-н е поглощает (в точке 1) падающий на него фотон и
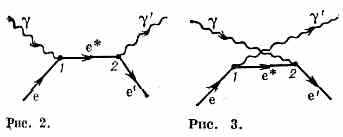
переходит из начального в нек-рое промежуточное (виртуальное) состояние е*, после чего виртуальный эл-н испускает (в точке 2) новый, конечный фотон ', а сам переходит в конечное состояние е'. Этот процесс можно представить в виде Фейнмана диаграммы, изображённой на рис. 2. Возможна и др. последовательность процесса: начальный эл-н сначала испускает конечный фотон и переходит в виртуальное состояние, а затем, поглощая начальный фотон, превращается в конечный эл-н (рис. 3). Испускание и поглощение эл-ном фотона происходят в результате вз-ствия эл-на с эл.-магн. полем, к-рое на диаграммах осуществляется в точках 1 и 2. Интенсивность комптоновского рассеяния зависит как от угла рассеяния, так и от длины волны падающего излучения. В угл. распределении рассеянных фотонов наблюдается асимметрия: больше фотонов рассеивается по направлению вперёд, причём эта асимметрия увеличивается с ростом ξ. Полная интенсивность (или сечение ) комптоновского рассеяния падает с ростом ξ. Зависимость от ξ даётся ф-лой Клейна — Нишины, представляющей собой результат расчётов, отвечающих двум диаграммам Фейнмана на рис. 2 и 3. Эту ф-лу можно записать в виде: =T[1-f()], где T=8/3r20 — сечение томсоновского рассеяния, r0=е2/mес22,8•10-13 см— т. н. классич. радиус эл-на, — энергия падающих фотонов в ед. mес2 (=ξ/mес2), а f() — ф-ция, возрастающая при увеличении . При малых энергиях фотона f()0 и =Т7•10-24 см2. С ростом уменьшается и при очень высоких оно падает до нуля, т. к. в этом случае f()1 (рис. 4).
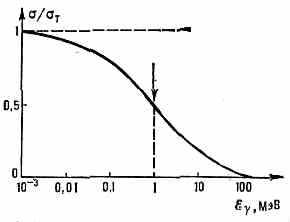
Рис. 4. График зависимости полного сечения о комптон-эффекта (в ед. сечения классич. рассеяния T) от энергии фотона ξ ; стрелка указывает энергию, при к-рой начинается рождение электрон-позитронных пар.
Такая зависимость сечения от энергии определяет место К. э. среди др. эффектов вз-ствия излучения с в-вом, ответственных за потери энергии фотонами при их пролёте через в-во. К. э. даёт гл. вклад в энергетич. потери фотонов в свинце при ξ порядка 1—10 МэВ (в более лёгком элементе — алюминии этот диапазон составляет 0,1—30 МэВ); ниже этой области с ним успешно конкурирует фотоэффект, а выше — рождение пар (см. рис. 2 в ст. Гамма-излучение).
Комптоновское рассеяние широко используется в исследованиях -излучения ат. ядер, лежит в основе принципа действия нек-рых гамма-спектрометров и др.
К. э. возможен не только на эл-нах, но и на др. заряж. ч-цах, напр. на протонах, однако из-за большой массы протона отдача его заметна лишь при рассеянии фотонов очень высокой энергии.
Обратный Комптона эффект. Если эл-ны, на к-рых упруго рассеивается эл.-магн. излучение, релятивистские, то энергия (и импульс) фотонов будет увеличиваться за счёт энергии (и импульса) эл-нов, т. е. длина волны при рассеянии будет уменьшаться. Это явление наз. обратным К. э. Его часто привлекают для объяснения механизма рентг. излучения косм. источников, образования рентг. компоненты фонового галактич. излучения, трансформации плазм. волн в эл.-магн. волны высокой частоты.
• Б о р н М., Атомная физика, пер. с англ., 3 изд., М., 1970; Фейнман Р., Теория фундаментальных процессов, дер. с англ., М., 1978.
В. П. Павлов.
КОМПТОНОВСКАЯ ДЛИНА ВОЛНЫ, величина размерности длины, характерная для релятив. квант. процессов;
выражается через массу т ч-цы и универсальные постоянные А и с: 0=h/mc. Назв. К. д. в. связано с тем, что 0 определяет изменение длины волны эл.-магн. излучения при комптоновском рассеянии на эл-не (см. Комптона эффект). Чаще К. д. в. называют величину 0=ћ/mc. Для эл-на 0З,9•10-11 см, для протона 02,1•10-14 см.
К. д. в. определяет масштаб пространств. неоднородностей полей, при к-рых становятся существенными квант. релятив. процессы. Напр., если рассматривается эл.-магн. поле, длина волны к-рого меньше К. д. в. эл-на, то энергия квантов этого поля ξ=h (где =c/ — частота) оказывается больше, чем энергия покоя эл-на mec2((ξ=hc/>mee2), и, следовательно, в этом поле становятся существенны процессы рождения электрон-познтронных пар, к-рые описываются релятив. квант. теорией поля.
К. д. в. определяет также расстояние, на к-рое может удалиться виртуальная частица массы т от точки своего рождения. Поэтому радиус действия яд. сил (определяемый самыми лёгкими из виртуальных адронов — -мезонами) по порядку величины равен К. д. в. -мезона (~10-13 см). Аналогично поляризация вакуума за счёт рождения виртуальных электрон-позитронных пар проявляется на расстояниях порядка
К. д. в. эл-на.
В. И. Григорьев.
КОНВЕКЦИОННЫЙ ТОК, перенос электрич. зарядов, осуществляемый перемещением заряж. макроскопич. тела. С точки зрения электронной теории, любой перенос зарядов в конечном счёте обусловлен конвекцией (перемещением) заряж. микрочастиц. Этим объясняется полная тождественность магн. св-в К. т. и тока проводимости (упорядоченного движения эл-нов, ионов и т. п.), установленная в опытах амер. физика Г. Роуланда (1879) и А. А. Эйхенвальда (1903).
КОНВЕКЦИЯ (от лат. convectio — принесение, доставка), перенос теплоты в жидкостях, газах или сыпучих средах потоками в-ва. Естественная (свободная) К. возникает в поле силы тяжести при неравномерном нагреве (нагреве снизу) текучих или сыпучих в-в. Нагретое в-во под действием архимедовой силы FA=gV ( — разность плотности нагретого в-ва и окружающей среды, V — его объём, g — ускорение свободного падения; см. Архимеда закон) перемещается относительно менее нагретого в-ва в направлении, противоположном направлению силы тяжести. К. приводит к выравниванию темп-ры в-ва. При стационарном подводе теплоты к в-ву в нём возникают стационарные конвекц. потоки. Интенсивность К. зависит от разности темп-р между слоями, теплопроводности и вязкости среды.
307
На К. ионизованного газа (напр., солнечной плазмы) существенно влияет магн. поле, степень ионизации газа и т. д.
При вынужденной К. перемещение в-ва происходит гл. обр. с помощью насоса, мешалки и др. устройств.
К. широко распространена в природе: в нижнем слое земной атмосферы, в океане, в недрах Земли, в звёздах.
КОНВЕРСИОННЫЕ ЭЛЕКТРОНЫ, электроны, испускаемые атомом в результате эл.-магн. перехода возбуждённого ат. ядра в состояние с меньшей энергией, когда избыток энергии ядро отдаёт одному из ат. эл-нов (см. Конверсия внутренняя).
КОНВЕРСИЯ ВНУТРЕННЯЯ гамма-излучения, явление, при к-ром энергия, высвобождаемая при эл.-магн. переходе возбуждённого- ат. ядра в состояние с меньшей энергией, передаётся непосредственно одному из эл-нов того же атома. При этом испускается т. н. к о н в е р с и о н н ы й э л е к т р о н. Эл-ны могут быть выбиты с разл. оболочек атома, и соответственно различают К-, L-, М- и т. д. эл-ны. Энергия эл-на равна разности энергии конвертированного яд. перехода и энергии связи электрона оболочки (небольшая доля энергии — сотые или тысячные доли % — передаётся конечному атому вследствие неизбежного эффекта «отдачи»).
Измерение энергетич. спектров конверсионных эл-нов позволяет определить энергию яд. переходов и их мультипольность.
Вероятность К. в. по отношению к вероятности перехода с испусканием -кванта характеризуется коэфф. внутр. конверсии — отношением интенсивности потока конверсионных эл-нов к интенсивности соответствующего -излучения. Коэфф. К. в. возрастает с уменьшением энергии перехода, ростом его мультипольности и заряда ядра. В зависимости от этих параметров коэфф. К. в. может меняться в широких пределах от ~10-2 — 10-3 до величин >>1. Для переходов между яд. состояниями со спинами, равными нулю, испускание -квантов запрещено правилами отбора и переход происходит только путём К. в. Сравнение измеренных коэфф. К. в. с рассчитанными теоретически — один из осн. методов определения мультипольностей переходов, спинов и чётностей яд. состояний.
При энергиях ξ яд. переходов, превышающих удвоенную энергию покоя эл-на (1,022 МэВ), может происходить К. в. с образованием электрон-позитронных пар (парная конверсия), вероятность к-рой растёт с ростом энергии и падает с увеличением мультипольности перехода (в отличие от К. в. на эл-нах атома). Спектры эл-нов и позитронов — непрерывные,
причем суммарная кинетич. энергия эл-на и позитрона равна ξ-2mc2 (m — масса электрона).
• Гамма-лучи, М.—Л., 1961; Альфа-, бета- и гамма-спектроскопия, под ред. К. Зигбана, пер. с англ., в. 3—4, М., 1969.
А. А. Сорокин.
КОНДЕНСАЦИЯ (от позднелат. condensatio — уплотнение, сгущение), переход в-ва вследствие его охлаждения или сжатия из газообразного состояния в конденсированное (жидкое или твёрдое). К. пара возможна только при темп-pax ниже критической для данного в-ва (см. Критическое состояние). К., как и обратный ей процесс — испарение, относится к фазовым переходам I рода. При К. выделяется то же кол-во теплоты, к-рое было затрачено на испарение сконденсировавшегося в-ва. Дождь, снег, роса, иней — следствия конденсации водяного пара в атмосфере. К. широко применяется в энергетике, в хим. технологии, в холодильной и криогенной технике, в опреснит. установках и т. д. В технике К. обычно осуществляется на охлаждаемых поверхностях. Известны два режима поверхностной К.: плёночный и капельный. Первый наблюдается при К. на смачиваемой поверхности и характеризуется образованием сплошной плёнки конденсата. На несмачиваемых поверхностях конденсат образуется в виде отд. капель. При капельной К. интенсивность теплообмена (отводы теплоты к поверхности охлаждения) значительно выше, чем при плёночной, т. к. сплошная плёнка конденсата затрудняет теплообмен (ср. Кипение).
Скорость поверхностной К. тем выше, чем ниже темп-pa поверхности по сравнению с темп-рой насыщения пара при заданном давлении. Наличие в объёме наряду с паром др. газа уменьшает скорость поверхностной К., т. к. газ затрудняет поступление пара к поверхности охлаждения. В присутствии неконденсирующихся газов К. начинается при достижении паром у поверхности охлаждения парциального давления и темп-ры, соответствующих состоянию насыщения (точке росы).
К. может происходить также внутри объёма пара (парогазовой смеси). Для начала объёмной К. пар должен быть заметно пересыщен. Мерой пересыщения служит отношение давления пара р к давлению насыщ. пара ps, находящегося в равновесии с жидкой или тв. фазой, имеющей плоскую поверхность. Пар пересыщен, если p/ps>1, при p/ps=l пар насыщен. Степень пересыщения =p/ps, необходимая для начала К., зависит от содержания в паре мельчайших пылинок (аэрозолей), к-рые явл. готовыми центрами К. Чем чище пар, тем выше должна быть нач. степень пересыщения. Зародышами, или центрами, К. могут служить также электрически заряжённые частицы, в частности ионизованные атомы, присутствующие в паре.
Кинетика процесса К. изучается теоретически как задача кинетики физической.
• Хирс Д., Паунд Г., Испарение и конденсация, пер. с англ., М., 1966; Исаченко В. П., О с и п о в а В. А., С укомел А. С., Теплопередача, 3 изд., М., 1975; Л и ф ш и ц Е. М., П и т а е в с к и й Л. П., Физическая кинетика, М., 1979 гл. 12.
КОНДЕНСИРОВАННОЕ СОСТОЯНИЕ вещества, твёрдое и жидкое состояния в-ва. В отличие от газообразного состояния, у в-ва в К. с. существует упорядоченность в расположении ч-ц (ионов, атомов, молекул). Крист. тв. тела обладают высокой степенью упорядоченности — дальним порядком в расположении ч-ц (см. Кристаллическая решётка). Ч-цы жидкостей и аморфных тв. тел располагаются более хаотично, для них характерен ближний порядок (см. Дальний и ближний порядок). Св-ва в-ва в конденсиров. состоянии определяются его структурой и вз-ствием ч-ц (см. Твёрдое тело, Жидкость).
КОНДЕНСОР, короткофокусная линза. или система линз, используемая в оптическом приборе для освещения рассматриваемого или проецируемого предмета. К. собирает и направляет на предмет лучи от источника света, в т. ч. и такие, к-рые в его отсутствие проходят мимо предмета, в результате резко возрастает освещённость предмета. К. применяются в микроскопах, спектральных приборах, проекционных аппаратах разл. типов. Конструкция К. тем сложнее, чем больше его апертура. При числовых апертурах до 0,1 применяют простые линзы; при апертурах 0,2—0,3 — двухлинзовые, выше 0,3 — трёхлинзовые К Наиболее распространён К. из двух одинаковых плоско-выпуклых линз.
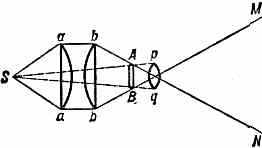
Схема проекц. аппарата с конденсором. S — источник света; ааbb — конденсор; АB -проецируемый предмет; pq — проекц. объектив; MN — экран.
к-рые обращены друг к другу сферич. поверхностями (рис.) для уменьшения сферической аберрации. Иногда поверхности линз К. имеют более сложную форму — параболоидальную, эллипсоидальную и т. д. Разрешающая способность микроскопа повышается с увеличением апертуры его К. Часто К. из неск. линз (с диафрагмой) используется в спектр. приборах для получения однородного освещения предмета при неоднородной структуре источника света.
• ТудоровскийА. И., Теория оптических приборов, 2 изд., т. 2, М.—Л, 1952.
308
КОНДО ЭФФЕКТ, аномальная температурная зависимость уд. электрич. сопротивления нек-рых нормальных металлов (Au, Ag, Cu, Al, Zn и др.): при понижении темп-ры уд. сопротивление этих металлов проходит через минимум при т. н. т е м п е р а т у р е К о н д о ТK, а затем возрастает, приближаясь к конечному пределу 0. К. э. обнаружен экспериментально в кон. 50-х гг., был объяснён япон. физиком Кондо в 1964. Причина К. э.— присутствие в металле примесных атомов Mn, Fe, Cr, Со и др. с незаполненными электронными оболочками, обладающими отличным от нуля магн. моментом (см. Парамагнетик). ТK варьируется в широком интервале, напр. в случае Zn с примесью Mn: TK=1К, а в Аl с примесью Mn: ТK=500К.
Рассеяние эл-на проводимости на парамагн. атоме может сопровождаться переворотом спинов эл-на и примесного атома. Своеобразный хар-р зависимости такого рассеяния от энергии эл-на проводимости и приводит к К. э. Рост уд. сопротивления при понижении темп-ры ниже ТK; прекращается, когда начинается упорядочение ориентации спинов примесных атомов, т. е. возникает ферромагнетизм или антиферромагнетизм. При этом ориентация спинов примесных атомов фиксируется и исчезает возможность рассеяния с переворотом спина. Др. проявление К. э.— уменьшение сопротивления в магн. поле, связанное с фиксацией спинов примесных атомов внеш. магн. полем. • Абрикосов А. А., Введение в теорию нормальных металлов, М., 1972.
Э. М. Эпштейн.
КОНИЧЕСКАЯ РЕФРАКЦИЯ, в кристаллооптике особый вид преломления пучка лучей света на грани двуосного кристалла, наблюдаемый в тех случаях, когда направление пучка совпадает с к.-л. оптич. осью б и н о р м а л ь ю или б и р а д и а л ь ю) такого кристалла. При К. р. каждый падающий на грань луч распадается на бесконечное число лучей, направленных по образующим конуса, вершина к-рого находится в точке падения луча на грань. К. р. была теоретически предсказана в 1832 ирл. математиком У. Р. Гамильтоном (обнаружена на опыте англ. физиком X. Ллойдом в 1833), применившим Гюйгенса — Френеля принцип при рассмотрении распространения света по указанным направлениям в двуосном кристалле. Пусть грани Р и Q пластинки, вырезанной из двуосного кристалла, перпендикулярны к одной из его оптич. осей (бинормали О1с, рис.). Если пучок неполяризованных параллельных лучей, падающих перпендикулярно на входную грань Р, пропустить через узкий прокол О1 в непрозрачном экране, то можно наблюдать внутреннюю К. р.— пучок будет расходиться из О1 внутри пластинки полым конусом с непрерывно меняющейся от участка к участку конуса линейной поляризацией световой волны (направления поляризации, т. е. направления колебаний вектора электрич. индукции, помечены точками и чёрточками на лучах и чёрточками на экране S).
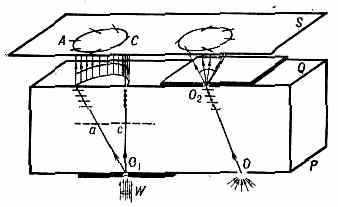
Преломившись на выходной грани Q, пучок образует в воздухе полый цилиндр, дающий светлое кольцо на 5. Внешнюю К. р. можно наблюдать с той же пластинкой. Если узкое отверстие О осветить рассеянным светом и через прокол О2 на выходной грани Q пропустить в воздух лучи, направления к-рых внутри кристалла очень близки к бирадиали, то из О2 будут тоже выходить пучки плоскополяризов. лучей, образующие полый конус с вершиной в О2.
К. р. испытывают только те немногие лучи, направление к-рых до преломления точно совпадает с направлением бинормали или бирадиали. Лучи же близких к ним направлений, гораздо более многочисленные, испытывают лишь обычное двойное лучепреломление, образуя внутри и вне слабо освещённых колец К. р. более яркие кольца.
• См. лит. при ст. Кристаллооптика.
КОНОСКОПИЯ (от греч. konos — конус и skopeo — смотрю, наблюдаю), изучение оптич. св-в кристаллов с помощью интерференц. фигур, наблюдаемых в верхней фокальной плоскости объектива поляризац. микроскопа.

Коноскопич. фигура двуосного кристалла в разрезе, перпендикулярном к биссектрисе острого угла между оптич. осями.
Каждая точка фигуры отвечает определ. направлению света, прошедшего через кристалл. В коноскопич. фигуре (рис.) на фоне изогнутых полос интерференц. окраски видны одна или две тёмные полосы (изогиры), по форме к-рых и их поведению при вращении столика поляризац. микроскопа можно определить осность кристалла, оценить величину угла между оптич. осями, расположение осей оптич. индикатрисы и др.
В. Б. Татарский.
КОНСЕРВАТИВНАЯ СИСТЕМА (от лат. conservo — сохраняю), механич. система, для к-рой имеет место закон сохранения механич. энергии, т. е. сумма кинетич. энергии Т и потенц. энергии П системы постоянна: T+П=const. Др. законы сохранения, напр. кол-ва движения, могут при этом не соблюдаться. Пример К. с.— Солн. система. В земных условиях, где неизбежно наличие сил сопротивления (трения, сопротивления среды и др.), вызывающих убывание механич. энергии и переход её в др. формы энергии, напр. в тепло, К. с. осуществляется лишь грубо приближённо.
КОНСТАНТА СВЯЗИ (константа взаимодействия), параметр, характеризующий силу взаимодействия ч-ц или полей. К. с. обычно определяется через амплитуду рассеяния двух ч-ц при данных (выбранных по соглашению) энергии и передаче импульса. При этом одним из наиб. важных требований, накладываемых на теорию, явл. независимость физ. результатов от изменения такого соглашения — т. н. р е н о р м а л н з а ц и о н н а я и н в а р и а н т н о с т ь (см. Перенормировка). По величине К. с. в физике элем. ч-ц различают сильное вз-ствие, характеризуемое безразмерной постоянной g2/ћc14, эл.-магн. вз-ствие, -характеризуемое величиной =e2/ћc1/137, а также слабое и гравитац. вз-ствия, характеризуемые соответственно величинами GFM2c/ћ3 и GМ2/ћс3,5•10-12. Здесь g — константа сильного вз-ствия, е—элем. электрич. заряд (константа эл.-магн. вз-ствия), GF — фермиевская константа слабого вз-ствия, G — гравитац. постоянная, М — масса нуклона.
В объединённой теории эл.-магн. и слабого вз-ствий константа GF выражается через постоянную и массу промежуточного векторного бозона. Имеется тенденция построения единой теории всех вз-ствий («великое объединение»), в к-рой все К. с. выражались бы друг через друга.
А. В. Ефремов.
КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ, разность потенциалов, возникающая между разными контактирующими проводниками в условиях термодинамич. равновесия. Если два тв. проводника привести в соприкосновение, то между ними происходит обмен эл-нами. В результате проводники заряжаются (с меньшей работой
309
выхода положительно, а с большей — отрицательно) до тех пор, пока потоки эл-нов в обоих направлениях не уравновесятся. Установившаяся К. р. п. равна разности работ выхода проводников, отнесённой к заряду эл-на. Если составить электрич. цепь из неск. проводников, то К. р. п. между крайними проводниками определяется только их работами выхода и не зависит от промежуточных членов цепи (правило Вольта). К. р. п. может достигать неск. В. Она зависит от строения проводника и от состояния его поверхности. Поэтому К. р. п. можно изменять обработкой поверхностей (покрытиями, адсорбцией и т. п.), введением примесей (для полупроводников) и сплавлением с др. в-вами (в случае металлов).
Электрич. поле К. р. п. сосредоточено вблизи границы раздела и в зазоре между проводниками. Линейные размеры этой области тем больше, чем меньше концентрации эл-нов проводимости в проводниках: в металлах ~10-8—10-7 см, в ПП до 10-4— 10-5 см.
Учёт К. р. п. существен при конструировании электровакуумных приборов. В электронных лампах К. р. п. влияет на вид вольтамперных хар-к. В термоэлектронном преобразователе энергии К. р. п. используется для прямого преобразования тепловой энергии в электрическую. К. р. п. обусловливает нелинейность вольтамперных хар-к контактов металл — ПП и св-ва электронно-дырочных переходов,
• П и к у с Г. Е., Основы теории полупроводниковых приборов, М., 1965; Царев Б. М., Контактная разность потенциалов и ее влияние на работу электровакуумных приборов, 2 изд., М., 1955.
В. Б. Сандомирский.
КОНТАКТНЫЕ НАПРЯЖЕНИЯ, напряжения, к-рые возникают при механич. взаимодействии тв. деформируемых тел на площадках соприкосновения тел и вблизи них (напр., при сжатии соприкасающихся тел).
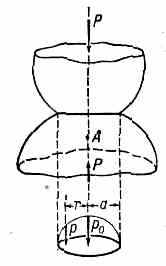
Распределение напряжений при сжатии сферич. тел: Р — сжимающая сила; p0 — макс. напряжение в центре площадки контакта; p — напряжение на расстоянии r от центра; а — радиус площадки; А — точка, в к-рой напряжение максимально.
Знание К. н. важно для расчёта на прочность подшипников, зубчатых и червячных передач, шариковых и цилиндрич. катков, соударяющихся тел
и т. п. Размер поверхности контакта часто мал по сравнению с размерами тел, причём К. н. быстро убывают при удалении от места контакта. Распределение К. н. по площадке контакта (рис.) и в её окрестности неравномерно, причём макс. касат. напряжения, к-рые в значит. мере предопределяют прочность сжимаемых тел, возникают на нек-ром удалении (точка А) от площадки контакта. КОНТРАГИРОВАННЫЙ РАЗРЯД (от лат. contraho — стягиваю, сжимаю), электрический разряд в газе, самосжатый в поперечном направлении, наблюдаемый при больших плотностях тока. Вдоль оси разрядной трубки наблюдается ярко светящийся тонкий токовый шнур, ионизация и плотность тока вне шнура невелики по сравнению со значением в шнуре. Осн. причины К. р.— термич. неоднородность и собств. магн. поле разряда. Первая причина играет роль преим. при давлениях порядка атмосферного. С ростом тока в радиально неоднородном столбе плазмы изменяются условия энергетич. баланса (в мол. газах, напр., при приближении диссоциации к полной резко увеличивается скорость переноса тепла) — в результате происходит контракция разряда. Это наблюдается при ср. плотности тока по сечению трубки ~5,3 мА/см2; плотность эл-нов по оси трубки при К. p. ~1011 см-3. Чем выше давление газа, тем при меньших токах может произойти переход к К. р. При низких давлениях К. р. обусловлен в основном магн. полем. При токах ~104—105 А (в атомарных газах) давление собственного магн. поля становится больше газокинетического и разряд переходит в К.р. (подробнее см. Пинч-эффект).
Л. А. Сена.
КОНТРАСТ (от франц. contraste — противоположность) в оптике, характеризует макс. различие в светимости разл. частей объекта. В геом. оптике
К. выражается как k=(Bмакс-Bмин)/Bмакс+Bмин) ,
где Bмакс и Вмин — макс. и мин. светимости (для объекта) или освещённости (для изображения), k изменяется от единицы (при Bмин=0) до 0 (при Вмин=Вмакс). Отношение =-k'/k, где k'— К. изображения, а k —К. предмета, наз. коэффициентом передачи К. через оптическую систему. При определении и обычно пользуются стандартным объектом — решёткой, состоящей из параллельных светлых и тёмных полос равной ширины. Вследствие аберраций и рассеяния света в оптич. системе к обычно меньше единицы и зависит от числа полос R на ед. длины в решётке. Функция (R) наз. частотно-контрастной характеристикой оптич. системы и наиболее полно описывает кач-во изображения.
Термин «К.» широко используется в др. областях оптики: ф о т о г р а ф и ч е с к и й К.— разность наибольшей и наименьшей оптич. плотностей; К. интерференционной картины — отношение разности яркостей в разл. её точках к соответствующей разности хода; цветовой К. служит хар-кой макс. различия в цветах объекта; зрительный К. характеризует особенность зрит. восприятия, в силу к-рой визуальная оценка яркости наблюдаемого объекта меняется в зависимости от окружающего фона либо от предыдущих зрит. впечатлений. Понятие «К.» используется в методе фазового контраста, к-рый состоит в пропорц. преобразовании разности фаз соседних частей пучка в разность интенсивностей. • Борн М., Вольф Э., Основы оптики, пер. с англ., М., 1973; Русинов М. М., Техническая оптика, Л., 1979.
А. П. Гагарин.
КОНЦЕНТРАТОР АКУСТИЧЕСКИЙ, устройство для увеличения интенсивности звука. К. а. подразделяются на низкочастотные и высокочастотные. Низкочастотный К. а. — устройство для увеличения амплитуды колебат. смещения низкочастотных УЗ излучателей; представляет собой отрезок стержневого звукопровода перем. сечения или перем. плотности, присоединяемый к излучателю более широким концом или концом с большей плотностью материала. Действие его основано на увеличении амплитуды смещения ч-ц стержня вследствие уменьшения поперечного сечения или плотности последнего в соответствии с законом сохранения кол-ва движения. Применяется гл. обр. на частотах от 18 до 44 кГц. Для эфф. работы низкочастотных К. а', должны выполняться соотношения D<'/2, l=n'/2, где n=l, 2, 3, ..., D — макс. поперечный, а l — продольный размер К. а., '— длина волны в нём. Применяются низкочастотные К. а. в УЗ технологии при резке, дроблении и диспергировании материалов, при сварке и т.д., а также в УЗ хирургии. Высокочастотный К. а.— устройство для увеличения плотности энергии в нек-рой части пр-ва по сравнению с плотностью энергии у поверхности УЗ излучателя. Действие его основано на фокусировке звука, поэтому в кач-ве К. а. могут быть использованы любые фокусирующие устройства — акустич. линзы, зеркала, зональные пластинки, рефлекторы, а также спец. К. а., к-рые представляют собой УЗ • фокусирующие излучатели, имеющие форму части сферы, прямого кругового цилиндра или трубы. Они могут создавать в фокальной области интенсивности до неск. кВт/см2 и даже МВт/см2 (т. н. сверхмощные К. а.). В сверхмощных К. а. применяется фокусирование как в жидкости, так и в тв. теле. Высокочастотные К. а. используют гл. обр. в УЗ технологии для эмульгирования, диспергирования, распыления, мойки, сушки и др.; в физике — для исследования действия мощного УЗ на
310
в-во; в биологии — для уничтожения микроорганизмов, исследования влияния УЗ на клетки и т. п., в эксперим. медицине — преим. в нейрохирургии.
И. Н. Каневский,
КОНЦЕНТРАЦИЯ (от новолат. concentratio — сосредоточение), величина, определяющая содержание компонента в смеси, р-ре, сплаве. Способы выражения К. различны. Долевая К. по массе — процентное отношение массы компонента к общей массе смеси (весовые %). Атомная (мольная) долевая К.— процентное отношение содержащихся в смеси грамм-атомов компонента к общему кол-ву грамм-атомов смеси (атомные, или мольные, %). О б ъ ё м н а я д о л е в а я К.— процентное отношение объёма компонента к общему объёму системы (объёмные %). К. жидких систем часто выражают массой в-ва, растворённого в 100 г или в 1 л растворителя, а также числом молей в-ва в 1000 молей растворителя. В учении о р-рах пользуются понятиями молярности (число молей в-ва в 1 л р-ра) и м о л я л ь н о с т и (число молей в-ва в 1 кг растворителя). К способам выражения К. относится также нормальность (число грамм-эквивалентов в-ва в 1 л р-ра) и титр (масса в-ва в 1 мл р-ра). В физике К. наз. кол-во ч-ц в ед. объёма.
К. определяют с помощью разл. хим. методов (напр., титрованием), методами спектрального анализа, лазерной спектроскопии, рентгеновской спектроскопии, поляриметрии и др.
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ в теории упругости и пластичности, увеличение напряжений в малых областях, примыкающих к местам с резким изменением формы поверхности тела, его сечения или с локализов. неоднородностью материала внутри тела. Факторами, обусловливающими К. н. (т. н. концентраторами напряжений или концентраторами), могут быть надрезы, выточки, выбоины, полости, усадочные раковины, трещины, инородные включения, царапины и т. п. К. н. может быть причиной разрушения тел, т. к. она снижает сопротивление тела ударным нагрузкам.
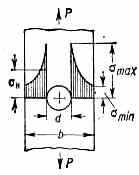
Концентрация напряжений при растяжении силой Р полосы шириной b с круглым отверстием диаметром d.
При удалении от концентратора напряжения убывают быстро (рис.).
Для количеств. оценки К. н. вводится понятие номинального напряжения н— напряжения, к-рое было бы при тех же нагрузках в теле без концентратора напряжений (напр., для
полосы с отверстием — равномерно распределённое норм. напряжение в той части полосы, где нет отверстия). Отношение макс. напряжения к номинальному в той же точке наз. коэфф. К.н. =макс/н, где под макс и н понимаются нормальные, или касательные напряжения, или их комбинация (напр., интенсивность напряжений). Значение коэфф. К.н. зависит от формы концентратора и его абс. и относит. размеров, типа нагрузки, структуры и механич. св-в материала. К существ. перераспределению напряжений и ослаблению эффекта К. н. приводит возникновение пластич. деформации в зоне концентратора напряжений.
Для уменьшения К. н. используются разгружающие надрезы, усиление зоны К. н. (напр., увеличение толщины' пластинки вокруг отверстия), технологич. приёмы упрочнения материала в зоне концентратора напряжений и т. п.
Распределение напряжений при наличии концентратора напряжений определяется методами теории упругости и пластичности, а также экспериментально (тензометрированием, методом лаковых покрытий, поляризационно-оптическим методом и др.).
В. С. Ленский.
КООРДИНАЦИОННАЯ СВЯЗЬ, то же, что донорно-акцепторная связь.
КООРДИНАЦИОННОЕ ЧИСЛО, число ближайших к данному атому соседних атомов в кристаллической решётке (атомной структуре кристалла) или молекул в молекулярных кристаллах. Если центры этих ближайших соседей соединить друг с другом прямыми линиями, то получится плоская фигура или многогранник, наз. координационными. Значение К. ч. колеблется от 2 до 14. Напр., в структуре алмаза, Ge, Si и ZnS К. ч. равно 4, координац. многогранник — тетраэдр. В структурах типа NaCl К. ч. равно 6, координац. многогранник — октаэдр. В нек-рых металлах (Cu, Au и др.) К. ч. равно 12, многогранник — кубооктаэдр. Понятие «К. ч.» применяется и при описании структуры аморфных тел и жидкостей. В этом случае оно явл. статистическим, поэтому К. ч. может оказаться не целым. Для жидкостей К. ч.— мера ближнего порядка; по тому, насколько К. ч. жидкости близко к К. ч. кристалла, судят о близости её структуры к структуре кристалла.
• См. лит. при ст. Кристаллохимия.
КОРИОЛИСА СИЛА, одна из сил инерции; вводится для учёта влияния вращения подвижной системы отсчёта на относительное движение материальной точки; названа по имени франц. учёного Г. Кориолиса (G. Coriolis). К. с. равна произведению массы точки на её Кориолиса ускорение и направлена противоположно этому ускорению. Эффект, учитываемый К. с., состоит в том, что во вращающейся системе отсчёта материальная точка,
движущаяся непараллельно оси этого вращения, отклоняется по направлению, перпендикулярному к её относит. скорости, или оказывает давление на тело, препятствующее такому отклонению. На Земле этот эффект, обусловленный её суточным вращением, заключается в том, что свободно падающие тела отклоняются от вертикали к востоку (в первом приближении), а тела, движущиеся вдоль земной поверхности, отклоняются в Сев. полушарии вправо, а в Южном — влево от направления их движения. Вследствие медленного вращения Земли эти отклонения весьма малы и заметно сказываются или при очень больших скоростях движения (напр., у ракет и у артиллерийских снарядов с большими дальностями полёта), или когда движение длится очень долго, напр, подмыв соответствующих берегов рек (т. н. закон Бэра), возникновение нек-рых возд. и мор. течений и др. В технике К. с. учитывается в теории гироскопов, турбин и мн. др. вращающихся систем.
• См. лит при ст. Механика.
С. М. Таре.
КОРИОЛИСА УСКОРЕНИЕ (поворотное ускорение), составляющая полного ускорения точки, к-рая появляется при т. н. сложном движении (см. Относительное движение), когда переносное движение, т.е. движение подвижной системы отсчёта, не является поступательным. К. у. возникает вследствие изменения относит. скорости точки vот при переносном движении и переносной скорости при относит. движении точки. Численно К. У. wкор=2перvотsin; как вектор К. у. определяется ф-лой wкор=2[перvот], где пер— угл. скорость поворота подвижной системы отсчёта относительно неподвижной, а — угол между vот и пер. Направление К. у. можно получить, спроектировав вектор vот на плоскость, перпендикулярную к пер, повернув эту проекцию на 90° в сторону переносного вращения. Таким образом, К. у.— это часть ускорения точки по отношению к основной, а не к подвижной системе отсчёта. Напр., при движении вдоль поверхности Земли вследствие её вращения точка будет иметь К. у. по отношению к звёздам, а не к Земле. К. у. равно нулю при поступат. переносном движении (пер=0) или когда =0.
• См. лит. при ст. Механика.
С. М. Тарг.
КОРОНА ВЫСОКОЧАСТОТНАЯ, высокочастотный коронный разряд, наблюдается на частотах 105 Гц. При частотах 10 МГц переходит в факельный разряд.
КОРОННЫЙ РАЗРЯД, высоковольтный самостоят. электрический разряд в газе при давлении p1 атм, возникающий в резко неоднородном электрич. поле вблизи электродов с большой кривизной поверхности (острия,
311
провода). В этих зонах происходят ионизация и возбуждение нейтр. ч-ц газа при их соударениях с эл-нами, в результате вокруг электродов возникает святящийся ореол — «корона». При пост. напряжении различают два вида короны: 1) униполярную (положительную или отрицательную), когда коронирует электрод только одного знака и во внеш. зоне движутся ионы этого же знака; если коронирует катод, во внеш. зоне в электроотрицат. газе движутся отрицат. ионы, в электроположительном — эл-ны; 2) биполярную, когда коронируют электроды обоих знаков и во внеш. зоне навстречу друг другу движутся ионы разных знаков.
Осн. процессами генерации эл-нов, обеспечивающими воспроизводство лавин и, следовательно, самостоятельность К. р., являются фотоэффект на поверхности электродов и объёмная фотоионизация собств. излучением разряда. Носители заряда, знак к-рых совпадает со знаком напряжения на коронирующем электроде, выносятся из зоны ионизации во внеш. зону, где условие самостоятельности разряда уже не выполняется. Объёмный заряд внеш. зоны ослабляет напряжённость поля в зоне ионизации и ограничивает силу тока короны. С увеличением приложенного напряжения сила тока увеличивается, но напряжённость электрич. поля на поверхности коронирующего электрода сохраняется неизменной, равной или близкой к напряжённости возникновения короны. В воздухе при атм. давлении напряжённость поля, при к-рой начинается К. р. на проводе радиусом 1 см, равна 39 кВ/см.
Структура зоны ионизации различна в зависимости от давления и рода газа, полярности и типа приложенного напряжения, размеров и формы коронирующего электрода. Она может быть непрерывной (напр., положит. К. р. на тонких проволоках) и прерывистой (К. р. на толстых проводах). При К. р. перем. тока конвективный ток, обусловленный движением объёмного заряда во внеш. зоне, замыкается на противолежащий электрод токами смещения. При напряжении с частотой 105 Гц возникает т. н. высокочастотная корона, резко отличающаяся от перечисленных выше структурой области ионизации и величиной тока.
Корона на проводах возд. линий электропередачи высокого напряжения приводит к потерям энергии. Прерывистый характер короны создаёт также дополнит. радиопомехи и акустич. шумы.
К. р. применяется в пром-сти, в электрофильтрах для очистки газов, а также в процессах т. н. электронно-ионной технологии при нанесении порошковых и лакокрасочных покрытий.
• Капцов Н. А., Электроника, 2 изд., М., 1956; Левитов В. И., Корона переменного тока, [2 изд.], М., 1975.
Н. Б. Богданова.
КОРПУСКУЛА (от лат. corpusculum — частица), ч-ца в классической (некваитовой) физике. Чаще употребляется прилагательное от К.— корпускулярный, т. е. обладающий св-вами ч-цы.
КОРПУСКУЛЯРНАЯ ОПТИКА, раздел физики, в к-ром изучаются законы движения заряж. ч-ц (эл-нов и ионов) в электрич. и магн. полях. Назв. «К. о.» отвечает аналогии, существующей между движением ч-ц в этих полях и распространением света в оптически неоднородных средах. Подробнее см. Электронная и ионная оптика.
КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ, лежащее в основе квант. теории представление о том, что в поведении микрообъектов проявляются как корпускулярные, так и волн. черты. По представлениям классич. (неквантовой) физики, движение ч-ц и распространение волн — принципиально разные физ. процессы. Однако опыты по вырыванию светом эл-нов с поверхности металлов (фотоэффект), изучение рассеяния света на эл-нах (Комптона эффект) и результаты ряда др. экспериментов убедительно показали, что свет — объект, имеющий, согласно классич. теории, волн. природу, обнаруживает сходство с потоком ч-ц — фотонов, обладающих энергией ξ и импульсом р, к-рые связаны с частотой v и длиной волны К света соотношениями: ξ=hv, p=h/. С др. стороны, пучок эл-нов, падающих на кристалл, даёт дифракц. картину, к-рую можно объяснить лишь на основе волн. представлений: со свободно движущимся эл-ном сопоставляется т. н. волна де Бройля, длина волны и частота к-рой связаны соотношениями =h/p, v=ξlh, где р — импульс, ξ — энергия эл-на. Позже было установлено, что это явление свойственно вообще всем микрочастицам (см. Дифракция микрочастиц). Такой дуализм корпускулярных и волн. св-в не может быть понят в рамках классич. физики; так, возникновение дифракц. картины при рассеянии ч-ц несовместимо с представлением о движении их по траекториям. Естеств. истолкование К.-в. д. получил в квантовой механике.
Д. В. Галъцов,
КОСМИЧЕСКАЯ ПЛАЗМА, плазма в косм. пространстве и в косм. объектах: звёздах, звёздных атмосферах, галактич. туманностях и т. п. Плазменное состояние — наиб. распространённое состояние в-ва во Вселенной.
В околоземном косм. пространстве К. п. можно рассматривать в известном смысле как плазму ионосферы, имеющую плотность n до ~105 см-3 на высотах ~350 км; плазму радиационных поясов Земли, (n~107 см-3) и магнитосферы; вплоть до неск. земных радиусов простирается т. н.
плазмосфера, характеризующаяся плотностью ч-ц ~102 см-3. Потоки солн. плазмы, двигающейся радиально от Солнца (т. н. солнечный ветер), по данным прямых измерений в космосе, имеют плотность ~(1—10) см-3. Наименьшими плотностями характеризуется К. п. в межзвёздном и межгалактич. пространстве (вплоть до n 10-3—10-4 см-3). В таких К. п., как правило, отсутствует термодинамич. равновесие, в частности между электронной и ионной компонентами. По отношению к быстропротекающим процессам (напр., ударным волнам) такие плазмы явл. бесстолкновительными.
Солнце и звёзды можно рассматривать как гигантские сгустки К. п. с плотностью, постепенно возрастающей от внеш. частей к центру, последовательно: корона, хромосфера, фотосфера, конвективная зона, ядро.
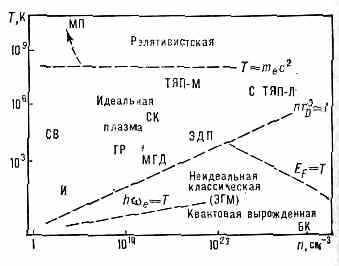
Классификация видов плазмы: ГР — плазма газового разряда; МГД — плазма в магнитогидродинамич. генераторах; ТЯП-М — плазма в термоядерных магн. ловушках; ТЯП-Л — плазма в условиях лазерного термоядерного синтеза; ЭГМ — электронный газ в металлах: ЭДП — электронно-дырочная плазма ПП; БК — вырожденный электронный газ в белых карликах; И — плазма ионосферы; СВ — плазма солн. ветра; GK — плазма солн. короны; С — плазма в центре Солнца; МП — плазма в магнитосферах пульсаров.
Макс., расчётная плотность К. п. в центре нормальных звёзд ~1024 см-3. В массивных и компактных звёздах плотность К. п. может быть на неск. порядков выше. Так, в белых карликах плотность настолько велика, что эл-ны оказываются вырожденными (см. Вырожденный газ). При ещё больших плотностях, как, напр., в нейтронных звёздах, вырождение наступает и для нуклонов.
К. п., как правило, явл. идеальным газом. Условие идеальности (малости энергии вз-ствия по сравнению с тепловой) автоматически выполняется в разреженных плазмах за счёт малости n; в глубинных частях нормальных звёзд — за счёт того, что тепловая энергия достаточно велика; в компактных вырожденных объектах — за счёт кинетич. Ферми энергии.
Шкала темп-р К. п. простирается от долей эВ в К. п. межзвёздной и межгалактич. сред до релятив. и ультрарелятив. темп-р в магнитосфе-
312
pax пульсаров — быстро вращающихся намагниченных нейтронных звёзд. На рис. схематически показано разнообразие видов К. п. и их примерное расположение на диаграмме темп-pa — плотность.
К. п. удалённых объектов исследуется дистанц. спектральными методами с помощью оптич. телескопов, радиотелескопов, а в последнее время и в рентгеновском и -излучениях с помощью внеатмосферных спутниковых телескопов. В пределах солн. системы быстро расширяется диапазон прямых измерений параметров К. п. с помощью приборов на спутниках и косм. аппаратах. Т. о. были обнаружены магнитосферы планет от Меркурия до Сатурна. Методы прямых измерений К. п. включают в себя использование зондовых, спектрометрических измерений и т. д. (см. Диагностика плазмы).
• Арцимович Л. А., Сагдеев Р. З., Физика плазмы для физиков, М., 1979; Пикельнер С. Б., Основы космической электродинамики, 2 изд., М., 1966; Акасофу С. И., Чепмен С., Солнечно-земная физика, пер. с англ., ч. 1—2,-М., 1974 — 75.
Р. З. Сагдеев.
КОСМИЧЕСКИЕ ЛУЧИ, поток элем. ч-ц высокой энергии, преим. протонов, приходящих на Землю прибл. изотропно со всех направлений косм. пр-ва, а также рождённое ими в атмосфере Земли в результате вз-ствия с ат. ядрами воздуха вторичное излучение, в к-ром встречаются практически все известные элем. ч-цы. Среди первичных К. л. различают высоко-энергичные (вплоть до 1021 эВ) галактические К. л. (ГКЛ), приходящие к Земле извне Солн. системы; и солнечные К. л. (СКЛ) умеренных энергий (1010 эВ), связанные с активностью Солнца.
Существование К. л. было установлено в 1912 австр. физиком В. Ф. Гессом по производимой ими ионизации воздуха; возрастание ионизации с высотой доказывало их внеземное происхождение; отклонение их в магн. поле (амер. физик Р. Э. Милликен, 1923; Д. В. Скобельцын, 1927; С. Н. Вернов, 1935) доказало, что К. л. представляют собой поток заряж. ч-ц. В 30—40-х гг. проводились интенсивные исследования вторичной компоненты К. л. с помощью камеры Вильсона, газоразрядных счётчиков, яд. фотоэмульсий. С 50-х гг. центр тяжести науч. исследований постепенно перемещается в сторону изучения первичных К. л. В 80-е гг. регистрация разл. компонент К. л. в широком диапазоне энергий проводится наземной мировой сетью станций (на уровне моря, в горах, шахтах), в стратосфере, на ИСЗ, на межпланетных автоматич. станциях.
В исследовании К. л. чётко выделяются два осн. аспекта — космофизический и ядерно-физический. В первом занимаются изучением природы К. л., их происхождения, состава, энергетич. спектров, временных вариаций, связи разл. явлений в К. л. с хар-ками среды, в к-рой происходит их движение; исследуются возможные источники К. л., механизмы ускорения ч-ц и т. п. Во втором направлении изучаются вз-ствия К. л. высоких энергий с в-вом, генерация элем. ч-ц в атмосфере и их св-ва. Этот аспект тесно примыкает к физике ч-ц высоких энергий. Именно детальное изучение зарядов и масс ч-ц вторичных К. л. привело к открытию таких элем. ч-ц, как позитрон, мюоны, - и К-мезоны, -гиперон. К. л. ещё долго будут оставаться уникальным источником ч-ц сверхвысоких энергий, т. к. в самых больших совр. ускорителях макс. достигнутая энергия пока ещё ~1014 эВ.
Энергетический спектр. Большое значение для определения источника К. л. имеет тщательное измерение их спектров. В интервале энергий от 1010 до 1015 эВ (рис. ) интегр. спектр всех
ч-ц ГКЛ описывается степенной ф-цией
ξ- с пост. показателем степени 1,7 (ξ — полная энергия). Как видно из этого выражения и рис., интенсивность тем больше, чем меньше энергия ч-цы. Однако при энергиях ξ<1010 эВ этот рост замедляется и практически совсем прекращается при ξ109 эВ (спектр становится плоским). Это значит, что в ГКЛ почти нет ч-ц очень малых энергий. При больших энергиях в интервале 1015— 1017 эВ падение интенсивности происходит быстрее, с 2,2. «Излом»

Энергетич. спектр косм. лучей: а — дифф. спектр протонов и ос-частиц умеренных энергий; б, в — интегр. спектры всех ч-ц в области высокой и сверхвысокой энергий. Точки — данные наблюдений.
