курс лекций

Вид материала

Задача Джонсона
Теорема Джонсона.
Задача о мультипроцессоре.
Эта задача может быть решена методом полного перебора вариантов
В результате мы получаем приемлемый по точности план загрузки
Планирование работ с возрастающей длительностью.

Подобный материал:

1 2 3 4 5 6 7 8

Задача Джонсона

Возникновение теории расписаний связано с постановкой и оригинальным решением задачи Джонсона (задачи о 2-х станках)

Дана система, включающая 2 станка, которая должна выполнить N

работ, каждая из которых является

двуэтапной (сперва на одном станке,

потом на другом)

Каждая работа характеризуется парой чисел – {τ1j; τ2j}, j=1-n (длительность работы на каждом станке)

Каждый этап каждой работы выполняется без прерываний если он начался, причем 2-ой этап начинается только после завершения 1-го этапа той же самой работы

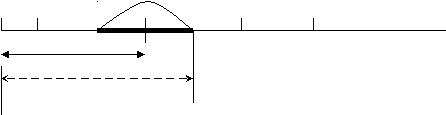
эт.1

э

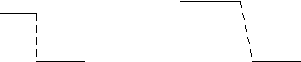т.1

эт.2 эт.2

Предполагается, что вторые этапы всех работ выполняются в той последовательности, что и первые.

Требуется построить расписание работы рассматриваемой двустаночной системы (календарный план), обеспечивающее минимизацию полного времени занятости этой системы выполнением работ.

Tcmin

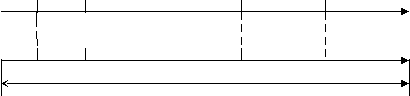τ11 τ12 τ1n-1 τ1n t1

τ21 τ22 τ2n-1 τ2n t2

0

Tc

При неудачном выборе последовательности работ появляются простои и задержки на 2-ом станке.

Подобные эффекты способствуют увеличению Тс.

Задача Джонсона стала знаменитой, т.к. удалось сформулировать условия существования расписания.

Теорема Джонсона.

Т: При возможном произвольном выборе № работ, порядок их производства, доставляющий min Тс в условиях рассматриваемой задачи, таков, что работа с порядковым номером v предшествует работе с № v+1, если min {τ1v;τ2,v+1} < min {τ2v;τ1,v+1}, где v=1,2,…,n-1.

Пример: Даны 5 двуэтапных работ, выполняемых в системе из 2-х станков. Длительности этапов работ заданы таблично.

Работы (произвольная №-ия)	Ι	ΙΙ	ΙΙΙ	ΙV	V
Продолжительность:
1-ый этап	6	0	5	8	2
2-ой этап	3	2	4	6	1

Требуется найти порядок выполнения работ в рассматриваемой системе такой, что полное время занятости системы минимально.

порядокmin Тс

Перестроим таблицу исходных данных:

Все τ1v;τ2v	0	1	2	3	4	5	6	8
1-й порядок работ	II	-	V	-	-	III	I	IV
2-й порядок работ	-	V	II	I	III	-	IV	-

Рассмотрим ряд предложений:

работа II занимает в будущем оптимальной последовательности выполнения работ v+1 позицию, это равносильно требованию:

min{τ1v;2}
эта работа II не может идти ни за какой другой работой, т.е. она должна попасть на 1-ое место в оптимальном порядке

Работа V занимает V позицию, т.е. опережает другую работу,

 min {2;τ2,v+1} < min{τ1,v+1;1}

min {2;τ2,v+1} <1- условие не выполняется, т.е. работа V должна занять последнюю позицию в оптимальном порядке.

Работа I занимает V позицию:

min {6;τ2,v+1}

Работа III занимает v позицию:

min {5;τ2,v+1}
Работа III после работы IV

Таким образом, оптимальная последовательность выполнения работ:

II  IV  III  I  V  min Tc = 23

Задача Бельмана-Джонсана-это задача Джонсона для n станков. Она не решена до сих пор.

Теория вычислительной сложности появилась в результате, т.к. она полезна, и для задач линейного программирования, и для других задач.

Главная задача теории - оценка того, является ли предложенный алгоритм решения задачи вычислительно эффективный, т.е. требующим умеренного объема работ.

Критерием эффективности является утверждение: если трудоёмкость алгоритма характеризуется экспоненциальной функцией от размерности задачи, то алгоритм является вычислительно не эффективный.

Задача о мультипроцессоре.

Мультипроцессором будем называть любую систему, объединяющую однотипные технологические единицы, способные выполнить заданные работы, т.е. многоканальная система.

Постановка задачи: дана система, объединяющая несколько однотипных процессоров (L); N работ с известными длительностями их выполнения (τj), причем каждая работа может быть выполнена на любом процессоре: известен момент начала работ (t0)

Требуется построить расписание для этой системы (план загрузки этой системы), доставляющий min времени занятости системы этими работами

(план)  min Tc

Tc – отсчитывается от момента (t0) до момента завершения последней работы.

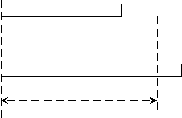
Г

ант-карта:

T1 N>>L- тогда задача имеет

смысл

1

Ti- времена занятости

отдельных процессоров

(i=1-L)

l

TL

.

. Tc=max Tl

.

1 l L

.

L

Эта задача может быть решена методом полного перебора вариантов

n

загрузки системы  2

Алгоритм решения этой задачи:

Среднее время загрузки процессов: Тср= (1/L)*(ΣТl)

ТсТср

min ТсТср  Идеальной схемой загрузки системы является любая схема, позволяющая достичь: min Тс=Тср ,  наша задача сводится, чтобы максимально равномерно загрузить процессы, т.е. это задача выравнивания загрузки всех процессов

Чтобы это доказать, надо рассмотреть сумму отклонений Т от Тср

((Тl-Тср)), которая будет = 0:

l

Σ (Тl-Тср)= Σ Тl - L Tср = Σ Тl -Σ Тl = 0

l l l l

Тогда алгоритм будет следующий:

1) вытянуть все работы в одну линию по возрастанию их длительности

r

I II N -1 N

Тср

τv

И рассмотреть Тср (отсечь). В зависимости от того, что больше I или II, мы отправим на 1-й процесс, либо r самых коротких работ, либо (r-1) работу.

τv – длительность перенумерованных работ (v = 1-N)

τr - I+II

r r

- Тср+Στv = II; Тср-Στv = I;

v=1 v=1

Если I>II, то r-работ на 1-й процессор.

2) Загрузка 2-го процессора по схеме шага 1

Предварительный план загрузки ПΙ системы получается в результате (L-1) шагов.

Характеристики ПI: max I

- время занятости наиболее загруженного процессора max Tl=Tl = Tc

1 l  L

min

- время занятости наименее загруженного процессора min Tl= Tl

1 l  L

L) наиболее и наименее загруженные процессоры

min

Tl

max

Tl

Тср

Попытаемся улучшить эти характеристики , путем перераспределения работ

max I I

между этими 2-мя процессорами (это надо, т.к. Tl = Tc , а Tc надо уменьшить) по предыдущей схеме  ПII. ПII всегда лучше ПI с т.зр. показателя Тс

Далее можно с ПII либо перейти к ПIII, либо оценка точности ПII.

δ =(maxTl-Tср)/Тср

Если δ - удовлетворительная, то не надо искать ПIII.

В результате мы получаем приемлемый по точности план загрузки

0

процессора П

После чего, мы можем поставить задачу нахождения точного решения (т.е. надо доказать, что найденное решение оптимально). Но это делать на практике не обязательно. Здесь возникает задача решения линейного уравнения в целых числах-диафантовых уравнений

Пример задачи о мультипроцессоре. Требуется построить оптимальный план загрузки системы (minТс)

L=4

N=7

Рабо-ты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
τj	54	60	60	72	75	78	90	90	96	108	111	120	120	123	135	150	150

Решение:

Тср=423; НОД τj = 3

Рассматриваем суммы величин τ:

1+τ2=114<Тср 6

τ1+τ2+τ3=174< Тср Tср -Στj =24

………………………. J=1

 на 1-й процессор идут

Т1=339 первые шесть работ

списка

Στj=339
J=1 Στj-Tср=66

J=1

7

Στj=489>Tср

J=1

Повторяем предыдущий шаг для оставшихся работ. На второй процессор идут работы 1-7 Т2=384 и т.д. На 3-й процессор идут работы 11-14 Т3=474, на 4-й процессор идут работы 15-17 Т4=435
П1: (предварительный план загрузки)

54,60,60,72,75,78 90,90,96,108 111,120,120,123 135,150,150

l=1 Т1=399 l=2 Т2=384 l=3 Т3=474 l= 4 Т4=435

Для плана оцениваем

max Тl=Т3=474 min Тl = T2=384

l l

Т3-Т2=90

Встает задача уравнения загрузки 3-го и 2-го процессора

2

3 45

90

Если будет: 90,90,96,108 111,120,120,123

L=2 Т2=384 l=3 T3=474 ,

То загрузка идеально выравнивается

П2:

54,60,60,72,75,78 90,108,111,120 90,96,120,123 135,150,150

l=1 T1=399 l=2 T2=429 l=3 T3=429 l=4 T4=435

max Тl=Т4=435 min Тl = T2=399 T4-T1=36

δ = (435-423)/423=12/423 3%

Если работа 60,72, с 1-го передать в обмен на 150 с 4-го, то будет новый план.

П3:

54,60,75,78,150 90,108,111,120 90,96,120,123 60,72,135,150

l=1 T1=417 l=2 T2=429 l=3 T3=429 T4=417

max Tl=T2=T3 = 429 min Tl=T1, T4=417

min-max=12

δ=6/423=1.5%

VII) Τl: 417 429

Т.к.ΗΟДτj, то ряд: 417,420,423,426,429 содержит точный план.

Это позволяет утверждать: для того, чтобы найти точное решение задачи достаточно решить уравнение вида:

Στjyj=B,

В - любое из чисел ряда

Yj – принимает значение 0/1.

Для этого можно рассмотреть таблицу вида:

№ строки	m B	3	4	5	6
1
2	. . .
3	Тср.=423.
4	. .

m-min и max кол-во отрезков τj, которое может образовывать В.

Все, что попадёт в строку №3, будет оптимальным решением. Если это строка будет пустой, то значит оптимальной будет соседняя строка.

Чтобы посмотреть эту таблицу для нашей задачи, надо рассмотреть 20 тыс. вариантов, т.е. мы в области резко растущей трудоёмкости.

Если бы мы это сделали, то получили бы решение:

(

60,72,90,90,111)

(120,120,108,75)

(150,54,123,96) max Тl = Тср = 423

(150,78,135,60)

(

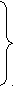60,75,78,90,120)

(150,54,111,108) max Тl =Тср = 423

(135,72,120,96)

(150,60,123,90)

Есть еще несколько идеальных решений.

Планирование работ с возрастающей длительностью.

Истощение инструментального ресурса приводит к возрастанию длительности работы.

Постановка задачи: Дана система однопроцессорная, с помощью которой должна быть выполнены N работ, которые характеризуются своими

номинальными длительностями (τj; j=1-N), т.е. если бы эта работа попала на первое место в очереди, то она была бы выполнена за это время τj

Если некоторая работа начинается в момент времени t>0, то её номинальная длительность увеличивается , то её номинальная длительность увеличивает

(t)

ся на некоторую величину τj

0 0 (t)

τj τm τm t

0 t>0 1 m  N

Требуется найти такой порядок выполнения работ, который обеспечил Тсmin

Предположим:

Закономерности возрастания длительности для всех работ одинаковы

0

(τj)

2) этот рост линейно зависит от t

τj

k

t

Решение:

Рассмотрим на оси времени 2 соседние по номерам работы: τv-1 τv

v-1 tv-1 tv t

0 (tv-1)

О

тсюда следует: tv=tv-1+τv+τv, v=2,3,…,N

Э

то разностное уравнение можно решить непосредственной подстановкой tv, для v=2,3,…,N.

0 0



t1=τ1, tv=τv+(1+k)tv-1 или

v-1 s 0

t

v=Σ(1+k)τv-s и

s=0

n-1 s o

Tc=Σ(1+k)τn-s

S=0 s

Чем дальше работа от конца, тем больше весовой коэффициент (1+к)

 оптимальный порядок: на первое место попадут самые короткие по номиналу работы.

Выводы:

Теория расписаний предлагает разные подходы к исследованию проблем организационного характера.

Задачи теории расписаний представляют практический и теоретический интерес, особенно в части решения проблем вычислительной сложности.
Важный, но малоизучаемый вопрос об учете различных неопределенностей в моделях календарного планирования ( случайных длительностей работ) открывает новые перспективы развития теории расписаний.

Blog