курс лекций

Вид материала

Простейший случайный поток (поток Пуасона).
Система массового обслуживания (СМО).
Простейшая модель обслуживания. Одноканальная СМО с отказом.
Возможные состояния простейшей СМО

Подобный материал:

1 2 3 4 5 6 7 8

Простейший случайный поток

(поток Пуасона).

Характерные особенности потока Пуасона:

случайная величина H распределена по зкону Пуасона:

()²

P(H = ) =   e^-^, где  = 0, 1, 2, …

!


P
- среднеожидаемое значение H (математическое ожидание H) или интенсивность потока

в

ремя T как случайная величина распределена по показательному закону:

f(t) = e^-^, t  (0; )

f(t)

1

поток стационарен (так как P(H = ) не зависит от t) и без последействия.

Верно для данного потока, что:

P(H  2)

Lim  = 0 выразитель свойства ординарности

0 P(H = 1)

Система массового обслуживания (СМО).

Любая система, подвергающаяся воздействию потока событий и реагирующая на это тем, что как-то преобразует этот поток и порождает новый поток событий, может быть названа СМО.

исходящий

поток

СМО

входящий

поток

Простейшая модель обслуживания.

Одноканальная СМО с отказом.

Предположим:

дана СМО, способная обрабатывать поступающие заявки только в последовательном режиме (то есть одноканальная)

аявки (события)

______

входящий поток заявок – Пуасоновский с интенсивностью 
исходящий поток формируется при условии, что время обслуживания каждой заявки в системе, являясь случайным, распределено по показательному закону с параметром  (вместо )

f(t) = e^-^^t

 - интенсивность обслуживания

заявка, пришедшая в систему и заставшая ее занятой, покидает систему (не дожидаясь обслуживания, получает отказ).

В этих условиях требуется определять характеристики рассматриваемой СМО (вероятность отказа, пропускную способность и др.) и тем самым построить формальную модель системы.

Общий подход к исследованию СМО, в том числе и этой, предполагает рассмотрение возможных состояний СМО в разные моменты времени и условий их перехода из одного состояния в другое.

Возможные состояния простейшей СМО:

S₀ – система свободна;
S₁ – система занята обслуживанием заявки.

Переход из одного состояния в другое происходит:

- из S₀ в S₁ с интенсивностью 

- из S₁ в S₀ с интенсивностью 

Схема возможных состояний и переходов для данной СМО:





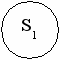
t - t t t + t t

t - мало

Какова вероятность того, что в произвольно взятый момент времени t система окажется в состоянии S₀?

Это условие будет верно, когда:

либо потому, что была в S₀и за t осталась в нем;
либо была в состоянии S₁, но за t стала S₀.

Такая логика дает возможность получить систему дифференциальных уравнений, описывающих процесс, происходящий в системе.

dp₀(t)

 =  - (+ )p₀(t) - система была бы, если бы было много состояний

dt

Условие: P₀ = 1 при t = 0

Решением уравнения будет:

 

P0 =  +   e^-(^⁺^^)t

 +   + 

Из условия P₀ + P₁ = 1 следует, что:



P1 =   (1 – e^-(^⁺^^)t)

 + 

P₀

P₁,P₀

P₁
  

/+

/+

P₁,P₀

/+

P₁

P

t

1

P₀
  

P₀

/+

P₁

1

t

  

//

С течением времени система выходит на стационарный режим работы, который характеризуется неизменностью значений P₁ и P₀ и они равны:

P₀^стац = /; P₁^стац = /

Характеристики:

вероятность отказа в обслуживании равна вероятности того, что в произвольно взятый момент времени система окажется занятой обслуживанием заявки, то есть

P_отк = P₁^стац = /

относительная пропускная способность системы – доля обслуженных заявок от общего числа пришедших заявок:

q_отн = P₀^стац = /

Если , то система начинает не справляться со своими задачами, и вероятность отказа начинает стремиться к единице.

Если , то система будет почти всегда свободна и относительная пропускная способность будет стремиться к единице.

Если , то каждая пришедшая заявка с вероятностью 0,5 будет либо обслужена, либо получит отказ.

Пример:

Пусть должно быть P_отк  0,1, то есть

/  0,1,  10  .

Blog

Простейший случайный поток

(поток Пуасона).

Система массового обслуживания (СМО).

Простейшая модель обслуживания.

Одноканальная СМО с отказом.