Московский Авиационный Институт (Государственный Технический Университет) «маи» Факультет №5 «Экономики и менеджмента» Кафедра 506 «Системы управления экономическими объектами» курс лекций
| Вид материала | Курс лекций |
| Прибыльные матрицы Задания и ответы 4. Теория массового обслуживания. Характеристикой случайного потока H является главной характеристикой любого потока |
- В. М. Трембач московский авиационный институт (государственный технический университет), 33.33kb.
- Государственное Образовательное Учреждение высшего профессионального образования Московский, 1556.11kb.
- Московский Авиационный Институт маи (Технический университет) Кафедра 804 курсовая, 264.85kb.
- Московский Государственный Институт Электроники и Математики (Технический Университет), 763.07kb.
- Московский государственный авиационный институт (технический университет), 121.53kb.
- Московский авиационный институт (государственный технический университет), 297.3kb.
- Московский Государственный Авиационный Институт им. Серго Орджоникидзе (технический, 292.9kb.
- Московский Государственный Институт Электроники и Математики (Технический Университет), 10.69kb.
- Московский Государственный Авиационный Институт (Технический Университет) реферат, 231.95kb.
- Московский Авиационный Институт (Государственный Технический Университет) Кафедра 104, 229.94kb.
Прибыльные матрицы
Предположим теперь, что отрасли закупают на внутреннем рынке системы (друг у друга) продукты, которые необходимы им как средства производства.
Пусть pi > 0 — цена единицы г-го продукта. Строка
p = (p1 p2 … pn),
каждый элемент которой является ценой единицы соответствующего продукта, производимого системой, называется строкой цен на продукты или ценовой строкой.
П
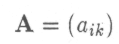
усть
-
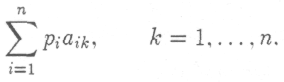
матрица материальных затрат системы. Тогда денежные издержки производства единицы k-ro продукта будут равны
Из этих величин и складывается матрица-строка рА издержек производства:
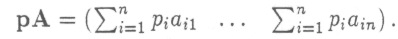
Квадратная матрица А ≥ 0 называется прибыльной, если существует такая строка р>0. что
Э
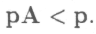
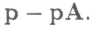
то означает, что существует хотя бы одна система цен р, при которой цена каждого продукта больше денежных издержек его производства и, следовательно, во всех отраслях обеспечивается положительная прибыль, выражаемая (в расчете на единицу продукции) разностью
Ясно, что возможность получения прибыли неразрывно связана с возможностью получения прибавочного продукта. Более того, условия продуктивности и прибыльности матрицы (материальных затрат) равносильны и всегда справедливо соотношение
о
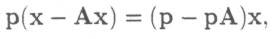
значающее, что прибыль есть лишь денежное выражение прибавочного продукта, а прибавочный продукт есть материальное выражение прибыли.
Задания и ответы
Сфера производства некоторой экономической системы состоит из двух отраслей. Найти оптимальный режим работы этих отраслей, обеспечивающих структуру прибавочного продукта, заданного столбцом с. при условии, что матрица материальных затрат А и строка рабочей силы 1 имеют следующий вид:

и известно, что мощность первой отрасли не превосходит 24, мощность второй отрасли не превосходит 12, а общее число рабочих L равно 120;

и известно, что мощность первой отрасли не превосходит 8. мощность второй отрасли не превосходит 12, а общее число рабочих L равно 90:
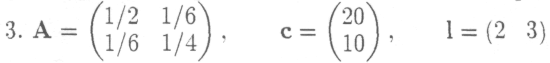
и известно, что мощность первой отрасли не превосходит 20, мощность второй отрасли не превосходит И, а общее число рабочих L равно 72;
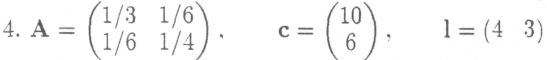
и известно, что мощность первой отрасли не превосходит 12. мощность второй отрасли не превосходит 8, а общее число рабочих L равно 96.
Ответы:
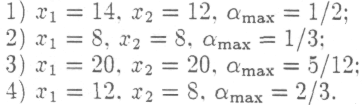
4. Теория массового обслуживания.
Разделяется на 2 раздела:
- теория потоков;
- теория систем массового обслуживания (СМО).
Потоки случайных событий: если события повторяются с течением времени, то можно говорить о потоке этих событий (явлений).
Если события, образующие поток, одинаковы в каком-то смысле (по форме проявления, по природе и т. д.), то поток называется однородным.
Если в некотором потоке события происходят через равные, возможно, наперед заданные промежутки времени, то он называется регулярным.
Если эти промежутки времени между событиями представляют собой случайную величину, то поток называется случайным.
Каковы средства описания свойств потока и что является предметом описания?
Существует графическое представление потоков, в котором на оси времени t размещаются случайным образом точки, символизирующие поток событий.





T
 t
t






Рассмотрим на этой оси некоторый случайный интервал длиной .
Количество событий, приходящихся на этот интервал, случайно, то есть являются случайной величиной с возможными значениями.
H – случайная величина – количество событий на интервале
= 0, 1, 2, …
Характеристикой случайного потока может служить функция распределения случайной величины H – F().
Случайная величина T – время между любыми двумя соседними событиями в потоке. Ее возможные значения: t от 0 до .
Тогда функция распределения случайной величины T – F(t) является второй важной характеристикой потока.
H – дискретная случайная величина
T – непрерывная случайная величина
H является главной характеристикой любого потока, так как зная ее закон распределения, мы можем широко охарактеризовать поток.
Поток является стационарным, если его характеристики не меняются со временем (при любой , F() – остается одной и той же).
Если в потоке соседние события не могут (хотя бы теоретически) повториться мгновенно, то такой поток называется ординарным (то есть событие произошло, потом поток “отдыхает”).
Если в потоке картина, наблюдаемая в разных непересекающихся интервалах 1 и 2, одна и та же в вероятностном смысле, то поток называется потоком без последействия.






0 1 2 t
То есть события интервала 1 не влияют на события интервала2.
