Московский Авиационный Институт (Государственный Технический Университет) «маи» Факультет №5 «Экономики и менеджмента» Кафедра 506 «Системы управления экономическими объектами» курс лекций
| Вид материала | Курс лекций |
| Ограничения на ресурсы L — общее число рабочих и- матрица-строка затрат рабочей силы Пусть дана продуктивная матрица |
- В. М. Трембач московский авиационный институт (государственный технический университет), 33.33kb.
- Государственное Образовательное Учреждение высшего профессионального образования Московский, 1556.11kb.
- Московский Авиационный Институт маи (Технический университет) Кафедра 804 курсовая, 264.85kb.
- Московский Государственный Институт Электроники и Математики (Технический Университет), 763.07kb.
- Московский государственный авиационный институт (технический университет), 121.53kb.
- Московский авиационный институт (государственный технический университет), 297.3kb.
- Московский Государственный Авиационный Институт им. Серго Орджоникидзе (технический, 292.9kb.
- Московский Государственный Институт Электроники и Математики (Технический Университет), 10.69kb.
- Московский Государственный Авиационный Институт (Технический Университет) реферат, 231.95kb.
- Московский Авиационный Институт (Государственный Технический Университет) Кафедра 104, 229.94kb.
Ограничения на ресурсы
Модель Леонтьева отражает те потенциальные возможности, которые заложены в технологии производственного сектора. В этой модели предполагается, что все промежуточные продукты к тому моменту, когда они оказываются необходимыми, уже произведены. Однако в реальной ситуации нужно принимать в расчет наличие таких ограничительных факторов производства, как мощность каждой отрасли (материальные ресурсы) и общее количество рабочей силы в системе (трудовые ресурсы).
П
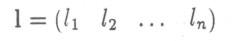 усть L — общее число рабочих и
усть L — общее число рабочих и- матрица-строка затрат рабочей силы: каждый ее элемент lk> 0 показывает количество рабочих, необходимое для производства единицы k-го продукта.
В
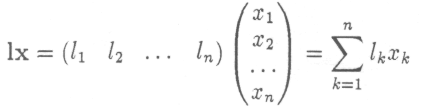
предположении линейности производства произведение
показывает количество рабочей силы, необходимое в сфере производства при режиме работы х.
Я
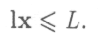
сно, что оно не может превосходить общего числа рабочих
О
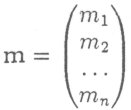
граничения на мощности отраслей можно описать при помощи столбца
превзойти который столбец выпуска не может,
х ≤ m.
При ограниченных ресурсах уженельзя ставить вопрос об удовлетворении любого конечного спроса с > О. Тем не менее продуктивная система может обеспечить любую структуру прибавочного продукта, т. е. соотношение между количеством прибавочных продуктов первой и второй отраслей.

ТЕОРЕМА. Пусть дана продуктивная матрица А > О, столбцы с > О и m > О, строка 1 > О я число L > 0. Тогда задача
имеет, и притом ровно одно, решение.
Рассмотрим на конкретном примере, как можно решать такую задачу.
Пример 3. Итак, даны
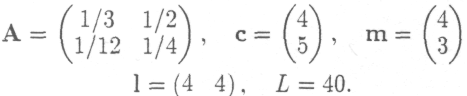
Начнем с решения системы
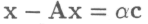
или подробнее:
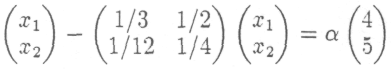
Это можно записать в равносильной форме:
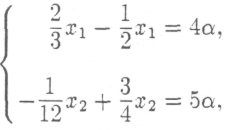
о

ткуда
и
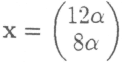
ли
Полученный столбец должен подчиняться условиям
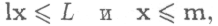
к

оторые в данном случае принимают вид:
Отсюда имеем:
и
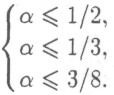
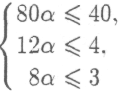
ли
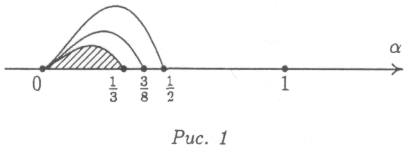
наибольшее значение а. удовлетворяющее всем трем условиям, равно 1/3 (рис. 1).
Ответ: атах = 1/3, столбец выпуска
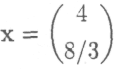
конечный
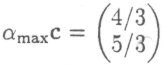
Замечание 1. Соотношение между количеством первого и количеством второго прибавочного продукта 4 : 5 -- то же, что и в случае отсутствия каких-либо ограничений на материальные и трудовые ресурсы.
З
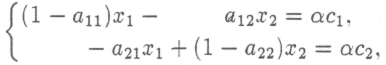

амечание 2. При п = 2 соотношения (1) принимают вид:
Решение системы уравнений можно записать так:
г

де b1 и b2 выражаются через элементы матрицы А и столбца с. Отсюда получаем
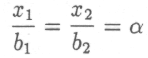
и

ли, исключая а,
Полученное равенство на плоскости (x1,x2) описывает прямую, проходящую через начальную точку 0(0,0).
В свою очередь, неравенства (2) можно проиллюстрировать так, как показано на
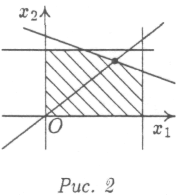
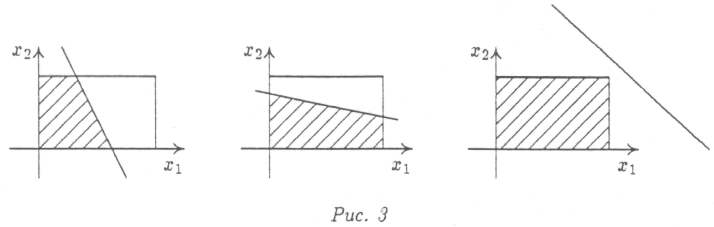
На рис. 3 представлены все возможные случаи.
Замечание. На рис.2 жирная точка отвечает Qmax.
