Московский Авиационный Институт (Государственный Технический Университет) «маи» Факультет №5 «Экономики и менеджмента» Кафедра 506 «Системы управления экономическими объектами» курс лекций
| Вид материала | Курс лекций |
- В. М. Трембач московский авиационный институт (государственный технический университет), 33.33kb.
- Государственное Образовательное Учреждение высшего профессионального образования Московский, 1556.11kb.
- Московский Авиационный Институт маи (Технический университет) Кафедра 804 курсовая, 264.85kb.
- Московский Государственный Институт Электроники и Математики (Технический Университет), 763.07kb.
- Московский государственный авиационный институт (технический университет), 121.53kb.
- Московский авиационный институт (государственный технический университет), 297.3kb.
- Московский Государственный Авиационный Институт им. Серго Орджоникидзе (технический, 292.9kb.
- Московский Государственный Институт Электроники и Математики (Технический Университет), 10.69kb.
- Московский Государственный Авиационный Институт (Технический Университет) реферат, 231.95kb.
- Московский Авиационный Институт (Государственный Технический Университет) Кафедра 104, 229.94kb.
Особенности сетевого графика
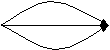
- каждая работа обозначается стрелкой , направление, которой отражает ход работы во времени
- отражены события «работа начата», «работа окончена».
- Стрелка-пунктир отражает отношение предшествования. Эти стрелки называются фиктивными работами
- Построенный граф можно не привязывать к временной сетки, что приводит к необходимости дополнительных поясняющих надписей.
Сетевой график представляет собой __ ориентированный граф, отражающий продолжительность выполнения работ и отношения предшествования, связывающее их.
Событие, которому не предшествует выполнение никакой работы из рассматриваемого комплекса работ, называется начальным событием.
Событие, за которым не следует никакое событие, называется конечным событием.
Работа, изображаемая стрелкой () называется простой работой.
Работа, которая допускает распараллеливание, т.е. возможно её представление несколькими стрелками, называется составной.
Р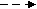 абота, обозначаемая , называется фиктивной
абота, обозначаемая , называется фиктивной
Последовательность работ – стрелок такая, что начало очередной работы в ней совпадает с окончанием предыдущей работы, называется путем в данном сетевой графике.
Путь максимальной длины называется критическим путем. Длина его Df продолжительность выполнения всего комплекса работ.
Смысл сетевого планирования заключается в такой организации работ, которая позволяет минимизировать длину критического пути.
Работы, образующие критический путь, называется критическими.
Анализ сетевых графиков не представляет какой-либо математической сложности и поэтому все расчеты на сегодня автоматизированы, а теория сетевого планирования прекратила своё развитие.
Заданные сроки выполнения работ на практике не выдерживают, тогда
- можно поводить анализ сетевых графиков при случайной продолжительности работ, но при этом случайно и τ, поэтому развития теория в этом направлении не получила (т.к. это сложно).
- можно говорить о диапазонах изменения длительности работ
3. Модель Леонтьева.
С помощью Модели Леонтьева можно определить эффективность производства экономической системы по имеющейся количественной информации об объеме необходимых затрат, неизбежно сопровождающих всякое производство.
Продуктивные матрицы
Пусть имеется экономическая система, сфера производства которой состоит из п отраслей, выпускающих п видов продукта, причем каждая отрасль выпускает ровно один вид.
Предположим, что для производства k-й отраслью единицы k-го продукта требуется аik ≥ 0 единиц i-го продукта, производимого i-й отраслью. Соответствующая таблица затрат выглядит так:
| | 1-й продукт | ... ... | k-й продукт | ... ... | n-й продукт |
| 1я отрасль | a11 | ... | a11 | | a11 |
| … … | ... | ... | ... | ... | ... |
| i-я отрасль | a11 | ... | a11 | ... | a11 |
| … … | ... | ... | ... | ... | ... |
| n-я отрасль | a11 | ... | a11 | ... | a11 |
или короче:

Полученная неотрицательная матрица А называется матрицей материальных затрат или технологической матрицей.
Замечание. Матрица А дает информацию о сложившейся структуре межотраслевых связей, о существующей технологии общественного производства и используется в текущем и долгосрочном планировании.
Будем считать дополнительно, что сложившаяся технология неизменна (стационарна) и что производство линейно. Последнее означает, что если для выпуска единицы k-го продукта требуется аik , единиц i-го продукта, то для выпуска xk единиц k-го продукта необходимо аik xk единиц i-го продукта.
Предположим, что за некоторый отрезок времени, фиксированный во всех дальнейших рассмотрениях (неделя, месяц, квартал или год), выпущено x1 единиц 1-го продукта, x2 единиц 2-го продукта, ..., хп единиц n-го продукта.
Т
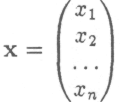
ем самым, задан столбец
называемый столбцом выпуска или режимом работы отраслей.
При заданном столбце выпуска х совокупные затраты i-го продукта в рассматриваемой производственной сфере равны
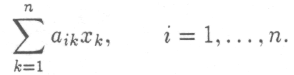
Из этих величин составляется столбец совокупных материальных затрат в сфере производства:
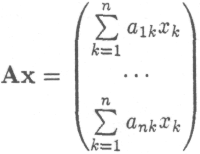
Матрица материальных затрат А ≥ 0 называется продуктивной, если найдется такой столбец выпуска х > 0, для которого выполняется неравенство
Ах < х.
Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором каждого продукта выпускается больше, чем затрачивается на его производство. Другими словами, при этом режиме сфера производства создает положительный столбец прибавочного (конечного) продукта:
х - Ах > О.
Возникает естественный вопрос: как следует поступить, чтобы сравнительно несложным путем и как можно раньше выяснить, является ли предъявленная матрица материальных затрат исследуемой сферы производства продуктивной или, напротив, производство убыточно и совокупные материальные затраты превышают объем выпуска?
Справедлив следующий общий факт.
ТЕОРЕМА. Для любой неотрицательной квадратной матрицы А ≥ 0 формулируемые ниже условия равносильны.
- Матрица А продуктивна.
- Для любого столбца с > 0 существует, и притом ровно один,
столбец выпуска х > 0 такой, что
х — Ах = с.
(3) Столбец выпуска х > 0, совокупные затраты на создание которого удовлетворяют условию
Ах ≥ х,
не существует.
(4) Наибольшее собственное значение матрицы А удовлетворяет неравенству
λА = λmax < 1.
Сказанное выше означает, что при выполнении хотя бы одного из этих условий выполняются и три остальных. В частности, выполнение неравенства
λА < 1.
позволяет утверждать, что матрица продуктивна.
В приводимых ниже примерах мы ограничимся рассмотрением случая, когда п = 2, т. е. сфера производства экономической системы состоит из двух отраслей.
П
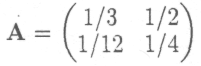
ример 1. Для ответа на вопрос, является ли матрица
продуктивной, найдем ее собственные значения Имеем:
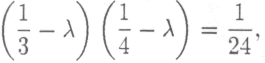
откуда
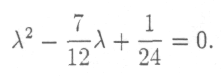
Корни этого уравнения легко вычисляются по формуле
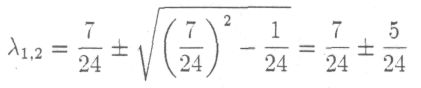
и
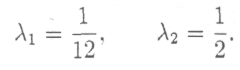
окончательно
Т
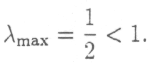
ем самым,
Ответ: матрица А продуктивна.
Из той же теоремы вытекает, что если матрица материальных затрат А продуктивна, то любой столбец прибавочного продукта может быть произведен при соответствующем режиме работы отраслей.
Итак, пусть матрица
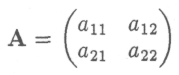
продуктивна и
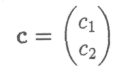
- столбец конечного продукта. Покажем, как найти режим работы отраслей, обеспечивающий этот продукт.
Запишем матричное равенство
х — Ах = с
более подробно:
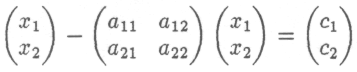
П
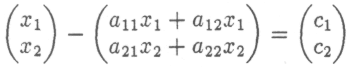
осле перемножения:
и
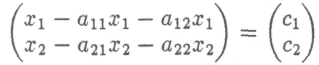
вычитания:
окончательно получим
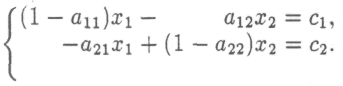
Для продуктивной матрицы построенная система имеет решение при любых с1 и с2.
Рассмотрим конкретный пример.
Пример 2. Пусть

К
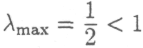 ак было установлено в примере 1, матрица А продуктивна, , и поэтому система
ак было установлено в примере 1, матрица А продуктивна, , и поэтому система и
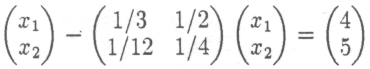
меет решение (всегда совместна).
П
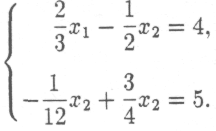
осле простых преобразований получаем:
Найдем решение этой системы методом исключения неизвестной. Умножая первое уравнение на 3/2 и складывая со вторым, получим

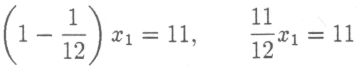
и далее
x1 = 12.
П
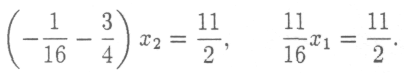
одобным же образом, умножая первое уравнение на
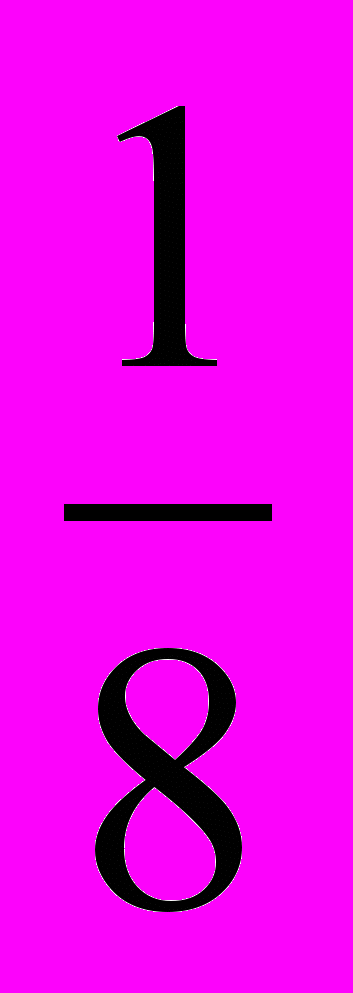 и складывая со вторым, находим значение второй неизвестной. Имеем:
и складывая со вторым, находим значение второй неизвестной. Имеем:Отсюда
x2 = 8.
Т
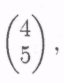
аким образом, для того чтобы обеспечить прибавочный продукт
н
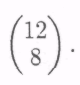
еобходимо, чтобы столбец выпуска был равен
