курс лекций

Вид материала

Подобный материал:

1 2 3 4 5 6 7 8

Формула Литтла

Это один из редких универсальных результатов ТМО, позволяющий проводить те или иные оценки систем в различных ситуациях

Ч

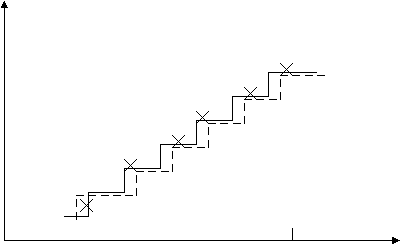исло заявок

4

3

2

1

0

Т t

- покидание системы заявкой

- поступление заявки

[0;Т]-наблюдается процесс обслуживания, который можно представить графически.

Пусть произвольна система, произволен входной поток заявок с интенсивностью λ; произвольное (в статистическом смысле) время обслуживания (μ). При этом все процессы являются стационарными.

Нт-среднее число заявок, обслуженных за время Т

λ=Нт/Т

Пусть, -время затраченное системой на обслуживание заявок в период Т

Формула Литтла

1/μ=τ=M/Т=υ

это характеризует интенсивность загрузки системы на интервале [0,Т]

υ>1 – система перегружена

υ<1 – система недогружена

Выводы:

ТМO изучает специфический класс систем, называемый СМО, на которых возлагаются следующие функции: преобразование потоков заявок в поток результатов обслуживания.

2 . ТМО изучает поведение СМО и их «производственных» характеристик.

Физическая природа СМО теорию не интересует.

3 . Большую роль в изучении СМО играют предположения, из которых вытекают оценки этих систем:

поток заявок – ексионенциальный
стационарный

- допустимость / недопустимость очередей

- и др.

 Нельзя абсолютизировать получаемые теоретические результаты

4. Известный исключением из общего правила относительности оценок системы явления формула Литтла, позволяющая дать обобщенную, но довольно грубую оценку работоспособности системы.

5. Аналитические зависимости, получаемые в результате исследования моделей массового обслуживания и служить основой разработки программных средств, позволяющих автоматизировать процессы исследований СМО, их проектирования и модернизации.

5. Теория календарного планирования (теория расписаний).

Теория Календарного планирования (КП) (теория расписаний) изучает проблемы рационального распределения времени, отводимого на производство тех или иных операций (действий, работ, мероприятий и т.д.)

Время является невостанавливаемым ресурсом и сточки зрения попытки рационального его распределения, основываются на производственно-экономических отношениях.

Расписанием (календарным планом) называется документ, содержащий сведения о:

количестве выполняемых операций;
момента начала и окончания каждой из заявленных работ
месте проведения каждой работы и используемом при этом оборудовании;
ограничениях, накладываемых на производимые работы;
возможных, дополнительных привлекаемых для производства работ, ресурсах.

Наиболее удобной формой представления расписания является Гантт-карта (графики Гантта): каждой работе ставится в соответствие отрезок нужной длины, изображающий в некотором масштабе длитнльность этой работы.

Каждая единица оборудования (каждому оборудованию ставится в соответствии ось времени, вдоль которой располагаются отрезки-работы, выполняемые на данном оборудовании)

Раб.1 Раб.2 Работа 3 t

Совокупность временных осей и создает общую картину выполнения заданного количества работ (графики Гантта), при установленном общем начале времени.

Гантт-карта отражает структуру произвольной системы.

Отличительной чертой задач КП является, в общем случае, отсутствие установленных отношений предшествования.

Простейшая задача теории расписаний.

Дана произвольная система, состоящая из единственного «исполнителя», который должен выполнить Ν работ.

Известны длительности работ τj (j=1-n ), система номеров, присваемая работам, произвольна.

Задан некий критерий оценки качества будущего расписания (К).

Требуется определить такую последовательность производства этих работ (т.е. календарный план), которая обеспечило бы минимальное (максимальное) значение К.

τ1 τ2 τn-1 τn t τj (j=1-n )

K min

Тс (max)

Тс- полное время выполнения заданных работ (время загрузки системы)

Если нужны перерывы между работами, то их можно включить в τj или выделить как отдельные работы.

Характеристики задач:

нет смысла бороться за Тс, т.к. оно постоянно и равно сумме Тj (т.е. отрицает экономию времени)
решении этой задачи при другом К, отличном от времени, наталкивается на трудность, связанную с большим количеством вариантов расписания (в пределе, кол-во вариантов расписания = N!)
в случае появления каких-то дополнительных условий, ограничивающих произвольный выбор варианта расписания, возникают «запрещенные» перестановки работ, поиск и отсеивание которых ведет к дополнительным трудностям.

Blog

Формула Литтла

Формула Литтла

5. Теория календарного планирования (теория расписаний).

Простейшая задача теории расписаний.