Московский Авиационный Институт (Государственный Технический Университет) «маи» Факультет №5 «Экономики и менеджмента» Кафедра 506 «Системы управления экономическими объектами» курс лекций

Вид материала

Курс лекций

Содержание Многоканальная система обслуживания с отказами. Одноканальная СМО с ограниченной очередью.

Подобный материал:

• В. М. Трембач московский авиационный институт (государственный технический университет), 33.33kb.
• Государственное Образовательное Учреждение высшего профессионального образования Московский, 1556.11kb.
• Московский Авиационный Институт маи (Технический университет) Кафедра 804 курсовая, 264.85kb.
• Московский Государственный Институт Электроники и Математики (Технический Университет), 763.07kb.
• Московский государственный авиационный институт (технический университет), 121.53kb.
• Московский авиационный институт (государственный технический университет), 297.3kb.
• Московский Государственный Авиационный Институт им. Серго Орджоникидзе (технический, 292.9kb.
• Московский Государственный Институт Электроники и Математики (Технический Университет), 10.69kb.
• Московский Государственный Авиационный Институт (Технический Университет) реферат, 231.95kb.
• Московский Авиационный Институт (Государственный Технический Университет) Кафедра 104, 229.94kb.

Многоканальная система обслуживания с отказами.

Многоканальность – способность обслуживать заявки в параллельном режиме.

заявки





СМО


1……………

.

r……………












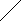
Каналы идентичны в смысле своих возможностей.

Поток обслуживания (результатов) формируется исходя из того, что каждый канал обслуживания имеет интенсивность .

То есть это объединение r простейших систем.

Предполагается, что заявка, пришедшая в систему и заставшая все каналы занятыми, получает отказ в обслуживании.

Требуется дать описание процессов, проходящих в системе, и определенные характеристики системы (вероятность отказа, q_отн и др.).

Схема состояний и переходов:

S₀ – система абсолютно свободна (все каналы свободны);

S₁ – в системе занят один канал, остальные свободны;

• 
  
• 
  
• 
  

S_r – система занята полностью (все r каналов).


  ………….



………..









 2 ……r…




…….


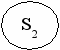
P₀ P₁ P_{2 …………………………} P_r






t

t t + t


Получим систему уравнений:




dP₀/dt = - P₀ + P₁

…………………….

dP_K/dt = -( + k)P_K + P_K-1 + (k+1)P_K+1

…………………….

dP_r/dt = - rP_r + P_r-1

k
= 1, 2, ……., r-1

P₀ = 1, P_K = 0 (k = 1, 2, ……., r) при t = 0


_r 1   P₀

P₀ = [ ( )^]^-1; P_K = ()^K  

^=0 !   r!

k = 1, ………., r


Характеристики:

1. P_отк = P_r = (/)^r(P₀ /r!)
   
2. q_отн = 1 - P_r = 1 – (/)^r(P₀ /r!)
   
3. среднее число заявок, обслуживаемых одновременно
   

n_одн^ср = (/)q_отн

Эта система значительно эффективнее (в r! раз), чем одноканальная.

Одноканальная СМО с ограниченной очередью.

………….

_______







СМО








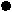
2 1

Допускается пребывание заявок, нашедших систему занятой, в очереди.

Длина этой очереди не должна быть больше некоторой величины .

Требуется: проанализировать процесс и найти характеристики системы.


Схема состояний и переходов





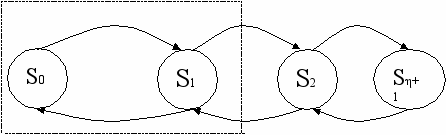
λ λ λ


μ μ μ

• перечень состояний одноканальной системы с отказом
  

S0 – система свободна

S0 - система занята

S0 - система занята и одна заявка в очереди

…..

Sη+1 – система занята и очередь наполнена





dp0 = - λρ0 + μ ρ1

dt

............

dp κ = - (λ + μ) ρκ + λ ρκ-1 + μ ρκ+1, κ = 1, 2, ..., η

dt

………

dpη+1 - μ ρη+1 + λ ρη

dt

η+1 α -1

Р0 = [ Σ (λμ) ]

α=0


κ

Рκ = (λ/μ) * ρ0, κ = 1, η + 1


Определим характеристики системы:

η+1

1. Ротк = Рη+1 = (λ/μ) * Р0
   

η+1

2. q отн = 1-P η+1 = 1 – (λ/μ) * Р0
   

Если λ=μ, то ρ0=ρη+1=1/(η+2)


Характеристики очереди:

Н-длина очереди

1. Средняя длина очереди
   

2 η-1

η = Σκρκ=(λ/μ)[ 1+2(λ/μ)+...+η(λ/μ) ]ρ0


Если λ=μ, то η1

2. Среднее время пребывания в очереди.
   

tоч=η/λ


Случай неограниченной очереди

η , тогда:

1. lim Р0=1-(λ/μ), при λ/μ < 1
   

lim Р0=0, при λ/μ  1


2

(λ/μ)

б) lim η= 1+λ/μ


2 -1

в) lim tоч= ( λ/μ )(1+λ/μ)