Проценко Ніна Федорівна, викладач правових дисциплін, спеціаліст вищої категорії Унавчально-методичному посібнику висвітлюються комплексно питання про закон
| Вид материала | Закон |
Содержание5.4.6. Еквіваленція, її умови істинності Логічні сполучники 5.4.7. Логічний закон, логічне протиріччя, виконувана формула А такий: 1. У складі формули А Метод аналітичних таблиць |
- Маляренко Світлана Олексіївна, спеціаліст вищої категорії, «старший учитель». «Нестандартні, 102.6kb.
- В. М. Захарова Використання інтерактивних методів навчання на урок, 682.45kb.
- Заступник директора з навчально-виховної роботи, вчитель математики вищої категорії,, 1763.48kb.
- Програма для вищих медичних навчальних закладів І-ІІ рівнів акредитації за спеціальністю, 2244.39kb.
- Вданій роботі подано методичні рекомендації, щодо використання методу проектів у курсі, 231.92kb.
- Програма вступного іспиту на базі освітньо-професійної програми підготовки молодшого, 194.52kb.
- Кияниця Ніна Віталіївна викладач української мови та літератури вищої категорії Тема,, 153.54kb.
- Довідка про підсумки проведення міських предметних олімпіад, 318.23kb.
- Формування ужиткових компетенцій при викладанні хімії Ряшина С.І., викладач вищої категорії,, 2216.75kb.
- Узгоджено: затверджую, 594.17kb.
5.4.5. Імплікація, її умови істинності
Розглянемо таке висловлювання, в якому описується обіцянка одного керівника:
«Якщо робітники поліпшать якість роботи, вони отримають премію».
Це складне висловлювання, складається з двох простих:
(1) «Робітники поліпшать якість роботи».
(2) «Вони отримають премію».
Його формула може бути записана як: р —>q (читається «Якщо р, тоді q»).
З метою визначення значення істинності цього складного висловлювання необхідно проаналізувати такі випадки:
І. Робітники поліпшили якість роботи і отримали за це премію, тобто і перше, і друге прості висловлювання виявилися істинними. Керівник дотримався свого слова і, відпо-відно, імплікація, висловлена ним, може бути оцінена як істинна.
2. Якість роботи поліпшена, але премія не отримана, тобто перше просте висловлювання — істинне, а друге — хибне.
У цьому випадку керівникові може бути пред'явлена претензія, що він не дотримався свого слова, вираженого за допомогою імплікації, і, отже, вона виявилася хибною.
3. Робітники якість роботи не поліпшили, але премію все-таки отримали, тобто перше просте висловлювання — хибне, а друге — істинне. Звичайно імплікація, яка складається з цих двох простих висловлювань, оцінюється як істинна, тому що керівник може видати премію робітникам і за інші заслуги, не входячи в протиріччя зі своєю обіцянкою, наприклад, за дисципліну на робочому місці.
4. Робітники не поліпшили якості роботи і не отримали премії, тобто перше і друге прості висловлювання — хибні.
У цьому випадку ніяких претензій пред'явити керівникові не можна. Хоча премії він і не видав, але своєї обіцянки при цьому не порушив. Оскільки робітники не поліпшили якості роботи, то це звільнює керівника від обіцянки преміювати їх. Звідси випливає, що імплікація у цьому випадку також може бути оцінена як істинна.
Таким чином, імплікація буде хибною лише тоді, коли перше висловлювання (антецедент) — істинне, а друге висловлювання (консеквент) — хибне. У всіх інших випадках імплікація є істинною.
Ці факти в таблиці істинності імплікації виражаються таким чином:
-
№№
А
В
А —>В
1
і
і
і
2
і
X
X
3
X
і
і
4
X
X
і
Виразу «А —>В» у природній мові та мові права, крім виразу «Якщо А, тоді В», відповідають численні синоніми: «А тоді, коли В», «У випадку А має місце В», «В, якщо А» тощо.
Наприклад, у висловлюванні: «Такими, хто не має судимості, визнаються люди, умовно засуджені, якщо протягом випробувального терміну вони не здійснять нового злочину...» (стаття 89 «Строки погашення судимості» Кримінального кодексу України) логічний сполучник «імплікація» використовується один раз і виражається за допомогою слова «якщо».
Дослідження імплікативних висловлювань має важливе значення для аналізу понять «необхідна умова» та «достатня умова» якоїсь події (ситуації, дії).
Умова вважається необхідною для даної події (ситуації, дії), якщо за її відсутності ця подія не відбувається. Наприклад: наявність атмосфери є необхідною умовою для виникнення існуючих на Землі видів тварин; успішне складання іспитів є необхідною умовою для вступу до вузу.
Висловлювання «А є необхідною умовою для В» фіксується за допомогою імплікацій: 1) В—>А; 2) ~А —> ~ В.
Умова вважається достатньою для даної події (ситуації, дії), якщо кожного разу, коли ця умова є наявною, дана подія може відбуватися і в деяких випадках відбувається. Наприклад: випадання дощу є достатньою умовою для того, щоб дахи будинків були мокрими; подання документів до приймальної комісії є достатньою умовою вступу до вузу.
Висловлювання «А є достатньою умовою для В» фіксується за допомогою імплікацій: 1) А—>В; 2) ~ В —>~ А.
Умови можуть бути «достатніми, але не необхідними», «необхідними, але не достатніми». Так, наприклад, подільність якогось числа на 2 є необхідною, але не достатньою умовою його ділення на 6, а подільність якогось числа на 10 є достатньою, але не необхідною умовою його ділення на 2.
Деякі умови для існування або виникнення певної події (ситуації, дії) можуть бути і необхідними, і достатніми. Для фіксації таких випадків застосовується логічний сполучник «еквіваленція».
5.4.6. Еквіваленція, її умови істинності
Розглянемо висловлювання, в якому вже згадуваний керівник дає робітникам таку обіцянку:
«Робітники отримають премію тоді і тільки тоді, коли вони поліпшать якість продукції».
Це складне висловлювання, складається з двох простих:
(1) «Робітники отримають премію».
(2) «Вони поліпшать якість продукції».
Його формула може бути записана таким чином: р <-> q (читається «р тоді і тільки тоді, коли р <-> q ).
Для визначення значення істинності цього складного висловлювання необхідно проаналізувати такі випадки:
1. Робітники поліпшили якість продукції і отримали премію. У цьому випадку керівник свою обіцянку виконав, він залишився вірний своєму слову, і, відповідно, складне висловлювання, яке він виголосив, є істинним.
2. Премію робітники отримали, але якість продукції не поліпшили. У цьому випадку керівник вчинив не відповідно до своєї обіцянки, бо він сказав, що робітники отримають премію тільки тоді, коли поліпшать якість, а вони якості не поліпшили. У зв'язку з цим його обіцянка може бути оцінена як хибна.
3. Премію робітники не отримали, а якість продукції поліпшили. Цей випадок аналогічний попередньому. Керівник не дотримав своєї обіцянки, і тому вона оцінюється як хибна.
4. Премію робітники не отримали і якість продукції не поліпшили. У цьому випадку ніяких претензій керівникові пред'явити не можна, бо він вчинив відповідно до своєї обіцянки. Тому складне висловлювання, яке виражає цей стан справ, може бути оцінене як істинне.
Таким чином, еквіваленція є істинною тоді і тільки тоді, коли обидва простих висловлювання, які входять до її складу, або одночасно істинні, або одночасно хибні. У випадку, коли одне з простих висловлювань є істинним, а друге — хибним, еквіваленція буде хибною.
Ці факти в таблиці істинності еквіваленції виражаються таким чином:
-
№№
А
В
А<->В
1
і
і
і
2
і
X
X
3
X
і
X
4
X
X
і
Виразу «А<->В» у природній мові і в мові права можуть відповідати такі вирази: «А тоді і тільки тоді, коли В», «А, якщо і тільки якщо В», «Якщо А, тоді В і навпаки», «А, якщо В, і В, якщо А», «для А необхідно і достатньо В», «А еквівалентне В» тощо.
Логічний сполучник «еквіваленція» інколи ще називають подвійною імплікацією, що є цілком закономірним з огляду на те, що еквіваленція фіксує необхідні і достатні умови деякої події (ситуації, дії).
Висловлювання «А є необхідною та достатньою умовою В» можна записати як застосовуючи логічний сполучник «еквіваленція»: А <-> В, так і застосовуючи логічний сполучник «імплікація»: 1) (А —> В)
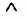 (В—> А); 2) (А—> В)
(В—> А); 2) (А—> В) 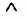 (~А —> ~ В).
(~А —> ~ В).Прикладом еквівалентного висловлювання у праві може бути визначення злочину в Кримінальному кодексі України. Відповідно до статті 11 будь-яке діяння слід розглядати як злочин у тому і тільки тому випадку, коли воно суспільно небезпечне й протиправне.
Логічні сполучники
-
Назва логічного сполучника
Знак логічного сполучника
Граматичний аналог логічного сполучника
1.Заперечення
~
«невірно, що...», «не» тощо
2. Кон'юнкція
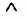
«і», «й», «а також» тощо
3. Диз'юнкція • слабка (нестрога диз'юнкція) • сильна (строга диз'юнкція)
V
«або», «чи», «а також» тощо «або... або», «чи ... чи» тощо
4. Імплікація

«якщо..., то..."
5. Еквіваленція
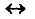
«...тоді і тільки тоді, коли...»
Зведена таблиця істинності для логічних сполучників
-
№
А
В
~А
АВ
АVВ
А В
В
А—>В
А<->В
1
і
і
х
і
і
х
і
і
2
і
х
х
х
і
і
х
х
3
х
і
і
х
і
і
і
х
4
х
х
і
х
х
х
і
і
5.4.7. Логічний закон, логічне протиріччя, виконувана формула
У сучасній логіці логічний закон — це вираз, який містить тільки логічні константи й змінні, тобто є формулою. Така формула повинна бути істинною у будь-якій предметній області, вона є завжди істинною формулою.
Сучасна логіка досліджує окремі логічні закони як елементи систем таких законів. Кожна із логічних теорій має безліч законів, за допомогою яких описується певний фрагмент або тип міркування.
Окрім логічних законів у будь-якій логічній системі виділяють ще такі види формул, як логічні протиріччя і виконувані формули.
Логічне протиріччя — це формула, яка буде хибною у будь-якій предметній області, вона є завжди хибною формулою.
Виконувана формула на відміну від логічного закону логічного протиріччя може змінювати своє логічне значення. У зв'язку з цим вона буває як істинною, так і хибною.
У логіці існують спеціальні методи, на основі яких можна завжди визначити статус формули, тобто з'ясувати, чи є вона логічним законом, логічним протиріччям або виконуваною формулою.
Метод таблиць істинності
Використовуючи таблиці істинності для логічних сполучників, можна побудувати такі самі таблиці для будь-якої формули логіки висловлювань, до складу якої входять декілька однакових або різних логічних сполучників.
Алгоритм побудови таблиці істинності для певної формули А такий:
1. У складі формули А виділяються усі під формули. Кожна підформула розпочинає новий стовпчик таблиці.
2. Вписуються в рядки всі можливі набори логічних значень пропозиційних змінних (простих підформул).
3. Обчислюється значення кожної складної підформули при кожному наборі значень змінних.
Значення простих підформул (пропозиційних змінних) здаються на основі формули 2". При обчисленні значень складних підформул використовуються табличні визначення логічних сполучників (~,
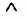 ,V, ,
,V, , —>, <->). Причому спочатку визначаються значення підформул, до складу яких входить один логічний сполучник, а потім підформул, до складу яких входять два логічних сполучника, і т. д. Наприкінці обчислюється значення підформули з максимальною кількісно логічних сполучників, тобто значення самої формули А.
—>, <->). Причому спочатку визначаються значення підформул, до складу яких входить один логічний сполучник, а потім підформул, до складу яких входять два логічних сполучника, і т. д. Наприкінці обчислюється значення підформули з максимальною кількісно логічних сполучників, тобто значення самої формули А.Якщо в результаті побудови таблиці істинності для формули А з'ясується, що ця формула набуває значення «істина» незалежно від того, які логічні значення набувають про-позиційні змінні, що входять до її складу, тоді така формула є логічним законом. У цьому випадку в останньому стовпчику таблиці (або в її результуючому стовпчику) повинні бути лише істинні значення.
Наприклад, побудуємо таблицю істинності для формули: р—> ( q —>p )
| №№ | Р | q | q —>Р | р—>(q—> р) |
| 1 | і | і | і | і |
| 2 | і | X | і | і |
| 3 | X | і | X | і |
| 4 | X | X | і | і |
На основі наведених таблиць можна визначити, що формула р—>(q—> р) є логічним законом.
Якщо в результаті побудови таблиці істинності для формули А з'ясується, що ця формула набуває значення «хиба» незалежно від того, які логічні значення набувають пропозиційні змінні, що входять до її складу, тоді така формула є логічним протиріччям. У цьому випадку в останньому стовпчику таблиці (або її результуючому стовпчику) повинні бути лише хибні значення.
Наприклад, побудуємо таблицю істинності для формули:
| № | р | q | q->p | p->(q->p) | ~(p->(q->p)) |
| 1 | і | і | і | і | X |
| 2 | і | X | і | і | X |
| 3 | X | і | X | і | X |
| 4 | X | X | і | і | X |
На основі наведених таблиць можна визначити, що формула ~ (р -> ( q -> p )) є логічним протиріччям.
І, нарешті, якщо в результаті побудови таблиці істинності для формули А з'ясується, що формула змінює своє логічне значення залежно від того, які логічні значення набувають пропозиційні змінні, що входять до її складу, тоді така формула є виконуваною формулою. У цьому випадку в останньому стовпчику таблиці (або її результуючому стовпчику) можуть бути як істинні, так і хибні значення.
Наприклад, побудуємо таблицю істинності для формули:
| №№ | Р | q | ~p | p->q | (p->q)V~p |
| 1 | і | і | X | і | і |
| 2 | і | X | X | X | X |
| 3 | X | і | і | і | і |
| 4 | X | X | і | і | і |
На основі наведених таблиць можна визначити, що формула: (р -> д) V ~ р є виконуваною формулою.
Метод аналітичних таблиць
Метод таблиць істинності є простим і природним методом для визначення статусу формули, якщо ця формула містить мінімальну кількість пропозиційних змінних. Однак він стає все більш громіздким при збільшенні числа пропозиційних змінних у формулі. Так, якщо формула міститиме З пропозиційні змінні, тоді рядків у таблиці вже повинно бути 23 = 8, якщо — 4 пропозиційні змінні, тоді — 24 = 16 і т. ін.
Подивіться, яку громіздку роботу необхідно провести для того, щоб дізнатися, що формула: р V (q
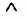 r ) є виконуваною.
r ) є виконуваною.| №№ | Р | q | r | q 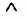 r r | p V (q 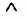 r ) r ) |
| 1 | і | і | і | і | і |
| 2 | і | і | X | X | і |
| 3 | і | X | і | X | і |
| 4 | і | X | X | X | і |
| 5 | X | і | і | і | і |
| 6 | X | і | X | X | X |
| 7 | X | X | 1 | X | X |
| 8 | X | X | X | X | X |
